2022-2023学年高一上学期数学人教A版(2019)必修第一册第4讲函数的表示法辅导讲义(无答案)
文档属性
| 名称 | 2022-2023学年高一上学期数学人教A版(2019)必修第一册第4讲函数的表示法辅导讲义(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 164.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-19 19:26:48 | ||
图片预览




文档简介
第4讲 函数的表示法
一、教学目标
1.掌握作函数图像的两种基本方法,学会用函数的图象解决相关问题
2.掌握常见函数解析式的求法,并能够熟练的应用
二、知识点梳理
知识点一:函数的三种表示方法
表示函数的方法,常用的有解析法、列表法和图象法三种.
解析法
圆的面积S是半径的函数,可用式子来表示,这种常把常量和表示自变量的字母用一系列的运算符号连接起来得到的式子叫做解析式
若在函数中,是用代数式表达的,则这种表达函数的方法叫做解析法。
图像法
用图像表示两个变量之间的对应关系的方法叫做图像法
函数图像的特征:函数图像既可以是连续的曲线,也可以是直线、折线、离散的点等等
3、列表法:
通过列出自变量与对应函数值的表格来表示函数关系的方法叫做列表法。
例如:初中学习过的平方表、平方根表、三角函数表。我们生活中也经常遇到列表法,如银行里的利息表,列车时刻表,公共汽车上的票价表等等都是用列表法来表示函数关系的.
函数的三种表示方法的优缺点比较
优点 缺点 联系
解析法 简明、全面地概括了变量间的关系. 通过解析式可以求出任意一个自变量所对应的函数值 不够形象、直观、具体,而且并不是所有的函数都能用解析式来表示 解析法、图象法、列表法各有优缺点,面对实际情境时,我们要根据不同的需要选择恰当的方法表示函数
列表法 不需要计算机就可以直接看出与自变量的值对应的函数值 只能表示出自变量取较少的有限值时的对应关系
图象法 能形象直观地表示出函数的变化情况 只能近似地求出自变量所对应的函数值,而且有时误差较大
例1、某种笔记本每个5元,买 x{1,2,3,4}个笔记本的钱数记为y(元),试写出以x为自变量的函数y的解析式,并画出这个函数的图像
解:这个函数的定义域集合是{1,2,3,4},函数的解析式为y=5x,x{1,2,3,4}. 它的图象由4个孤立点A (1, 5) B (2, 10) C (3, 15) D (4, 20)组成,如图所示
例2、 国内投寄信函(外埠),每封信函不超过20g付邮资80分,超过20g而不超过40g付邮资160分,依次类推,每封x g(0解:这个函数的定义域集合是,函数的解析式为
这个函数的图象是5条线段(不包括左端点),都平行于x轴,如图所示.
这一种函数我们把它称为分段函数
知识点二:函数图像的变换
作函数图象的基本步骤:列表、描点、连线;
变换作图法:
平移:“上加下减(y),左加右减(x)”
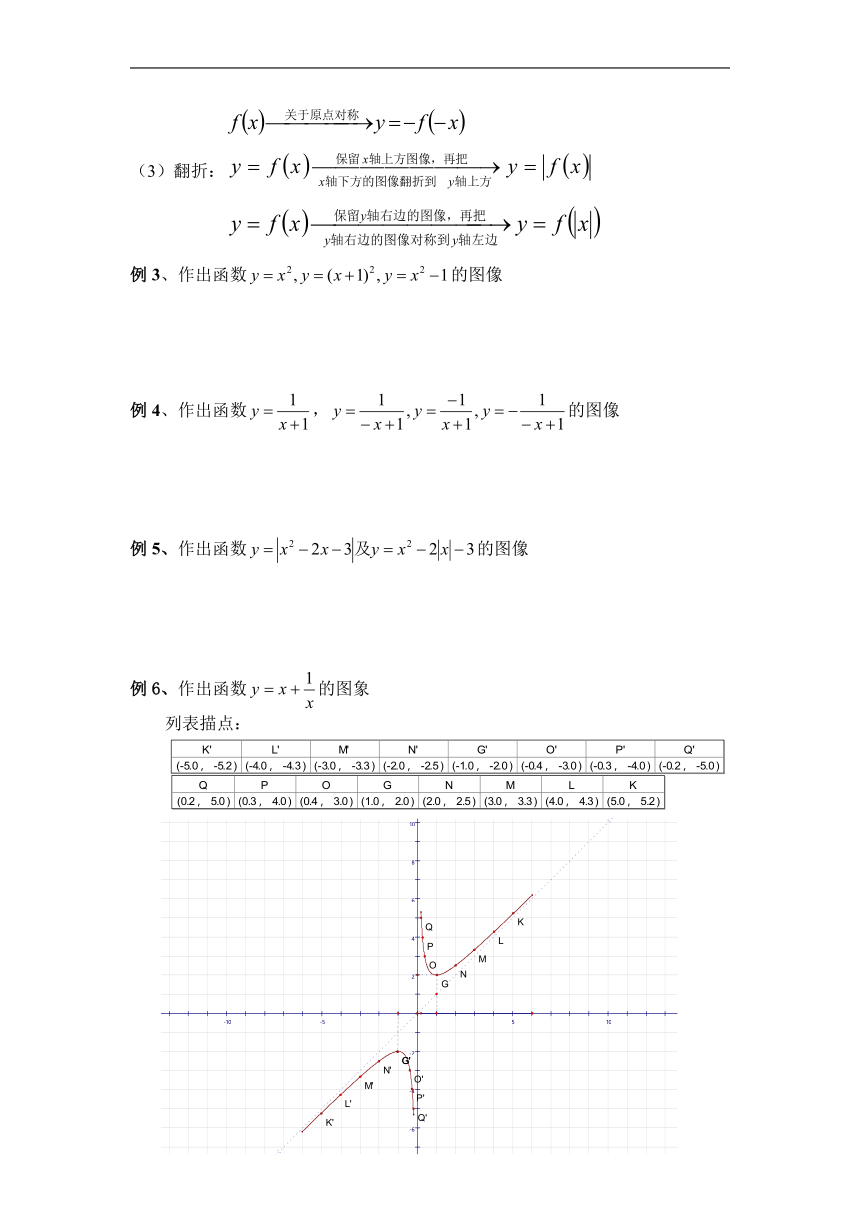
对称:, ,
翻折:
例3、作出函数的图像
例4、作出函数,的图像
例5、作出函数的图像
例6、作出函数的图象
列表描点:
知识点三:求函数的解析式的方法
由具体的实际问题建立函数关系求解析式,一般是通过研究自变量、函数及其他量之间的等量关系,将函数用自变量和其他量的关系表示出来,但不要忘记确定自变量的取值范围.
求函数解析式的常用方法有:代入法、配凑法、换元法、待定系数法、解方程组法或消元法、分段函数求解析式等。
代入法
例7、已知,求的解析式.
变式训练
已知,求的解析式.
配凑法
原函数的表达式为,是关于的式子,要求的解析式,这时要把通过变形、整理,使其变为只含有与常数的式子,然后将换成,即可得到的解析式,这种方法叫做配凑法.
例8、已知,求的解析式.
变式训练
已知,求;
换元法
解题时,把某个式子看做一个整体,用一个新的变量去代替它,从而使问题简化,这种方法叫做换元法.
例9、已知函数,求函数的解析式.
变式训练
已知,则的解析式为_________________.
待定系数法
有些问题中,常用字母来表示需要确定的系数,然后根据一些条件或要求确定这些系数,从而使问题得以解决,这种方法叫做待定系数法.
例10、如果,那么一次函数=_________________.
变式训练
1、已知是一次函数,且,求.
2、已知是二次函数,且满足,求.
解方程组法或消元法
在已知式子中,含有关于两个不同变量的函数,而这两个变量有着某种关系,这时就要依据两个变量的关系,建立一个新的关于两个变量的式子,由两个式子建立方程组,通过解方程组消去一个变量,得到目标变量的解析式,这种方法叫做解方程组法或消元法.
例11、已知,求的解析式.
变式训练
已知,求.
赋值法
在某些求函数解析式问题中,通过对自变量赋予特殊值,使其展现出其内在联系或减少变量个数,从而解决问题的方法叫做赋值法
例12、设是R上的函数,且满足,并且对任意实数,都有,求的解析式.
三、课堂练习
1、下列各图中,能作为的图象的是( )
A B C D
2、已知函数分别由下表给出:
1 2 3
1 3 1
1 2 3
3 2 1
则=__________,满足的的值是_______________.
一个面积为100的等腰梯形,上底长为,下底长为上底长的3倍,把它的高表示成的式子为( )
B. C. D.
某商场新进了10台彩电,每台售价3000元,试求出售出彩电数量x(台)与新进彩电销售总额y(元)之间的函数关系,分别用列表法、图像法、解析法表示出来。
5、求下列函数的解析式:
已知;(代入法)
已知f(x)是一次函数,且满足3f(x+1)-2f(x-1)=2x+17,求函数f(x)的解析式。(待定系数法)
已知f(2x+1)=3x-2,求函数f(x)的解析式。(配凑法)
已知;(换元法)
已知.(消去法)
四、课后作业
1、函数y = f (x) 的图象向左平移a(a>0)个单位,再向上平移b(b>0)个单位,所得图象的函数解析式是( )
A.y=f(x-a)+b B.y=f(x+a)-b C.y=f(x-a)-b D.y=f(x+a)+b
2、 一种产品的成本原来是a元,在今后m年内,计划使成本平均每年比上一年降低p%,成本y是经过年数x的函数(0<x<m),其关系式为( )
A.y=a(1+p%)x(0<x<m) B.y=a(1-p%)x(0<x<m)
C.y=a(p%)x(0<x<m) D.y=a-(p%)x(0<x<m)
3、( )
4、 已知函数y=f(x)的定义域为R,f(x-2)=f(3-x),则下列各式中与f(-1)相等的是( )
A.f(1) B.f(0) C.f(2) D.f(-2)
5、已知函数f(x)=3x-4的值域为[-1,5],则f(x)的定义域为______.
6、函数y=-2x+3(-2≤x<4)的值域为______.
7、已知函数f(x)满足,求函数f(x)的解析式。
8、已知,求函数f(x)的解析式。
9、已知,求函数f(x)的解析式。
10、已知,求函数f(x)的解析式。
11、已知f (x+1)=,求f (x)的解析式.
12、已知f (x)是二次函数,且,求f (x).
一、教学目标
1.掌握作函数图像的两种基本方法,学会用函数的图象解决相关问题
2.掌握常见函数解析式的求法,并能够熟练的应用
二、知识点梳理
知识点一:函数的三种表示方法
表示函数的方法,常用的有解析法、列表法和图象法三种.
解析法
圆的面积S是半径的函数,可用式子来表示,这种常把常量和表示自变量的字母用一系列的运算符号连接起来得到的式子叫做解析式
若在函数中,是用代数式表达的,则这种表达函数的方法叫做解析法。
图像法
用图像表示两个变量之间的对应关系的方法叫做图像法
函数图像的特征:函数图像既可以是连续的曲线,也可以是直线、折线、离散的点等等
3、列表法:
通过列出自变量与对应函数值的表格来表示函数关系的方法叫做列表法。
例如:初中学习过的平方表、平方根表、三角函数表。我们生活中也经常遇到列表法,如银行里的利息表,列车时刻表,公共汽车上的票价表等等都是用列表法来表示函数关系的.
函数的三种表示方法的优缺点比较
优点 缺点 联系
解析法 简明、全面地概括了变量间的关系. 通过解析式可以求出任意一个自变量所对应的函数值 不够形象、直观、具体,而且并不是所有的函数都能用解析式来表示 解析法、图象法、列表法各有优缺点,面对实际情境时,我们要根据不同的需要选择恰当的方法表示函数
列表法 不需要计算机就可以直接看出与自变量的值对应的函数值 只能表示出自变量取较少的有限值时的对应关系
图象法 能形象直观地表示出函数的变化情况 只能近似地求出自变量所对应的函数值,而且有时误差较大
例1、某种笔记本每个5元,买 x{1,2,3,4}个笔记本的钱数记为y(元),试写出以x为自变量的函数y的解析式,并画出这个函数的图像
解:这个函数的定义域集合是{1,2,3,4},函数的解析式为y=5x,x{1,2,3,4}. 它的图象由4个孤立点A (1, 5) B (2, 10) C (3, 15) D (4, 20)组成,如图所示
例2、 国内投寄信函(外埠),每封信函不超过20g付邮资80分,超过20g而不超过40g付邮资160分,依次类推,每封x g(0
这个函数的图象是5条线段(不包括左端点),都平行于x轴,如图所示.
这一种函数我们把它称为分段函数
知识点二:函数图像的变换
作函数图象的基本步骤:列表、描点、连线;
变换作图法:
平移:“上加下减(y),左加右减(x)”
对称:, ,
翻折:
例3、作出函数的图像
例4、作出函数,的图像
例5、作出函数的图像
例6、作出函数的图象
列表描点:
知识点三:求函数的解析式的方法
由具体的实际问题建立函数关系求解析式,一般是通过研究自变量、函数及其他量之间的等量关系,将函数用自变量和其他量的关系表示出来,但不要忘记确定自变量的取值范围.
求函数解析式的常用方法有:代入法、配凑法、换元法、待定系数法、解方程组法或消元法、分段函数求解析式等。
代入法
例7、已知,求的解析式.
变式训练
已知,求的解析式.
配凑法
原函数的表达式为,是关于的式子,要求的解析式,这时要把通过变形、整理,使其变为只含有与常数的式子,然后将换成,即可得到的解析式,这种方法叫做配凑法.
例8、已知,求的解析式.
变式训练
已知,求;
换元法
解题时,把某个式子看做一个整体,用一个新的变量去代替它,从而使问题简化,这种方法叫做换元法.
例9、已知函数,求函数的解析式.
变式训练
已知,则的解析式为_________________.
待定系数法
有些问题中,常用字母来表示需要确定的系数,然后根据一些条件或要求确定这些系数,从而使问题得以解决,这种方法叫做待定系数法.
例10、如果,那么一次函数=_________________.
变式训练
1、已知是一次函数,且,求.
2、已知是二次函数,且满足,求.
解方程组法或消元法
在已知式子中,含有关于两个不同变量的函数,而这两个变量有着某种关系,这时就要依据两个变量的关系,建立一个新的关于两个变量的式子,由两个式子建立方程组,通过解方程组消去一个变量,得到目标变量的解析式,这种方法叫做解方程组法或消元法.
例11、已知,求的解析式.
变式训练
已知,求.
赋值法
在某些求函数解析式问题中,通过对自变量赋予特殊值,使其展现出其内在联系或减少变量个数,从而解决问题的方法叫做赋值法
例12、设是R上的函数,且满足,并且对任意实数,都有,求的解析式.
三、课堂练习
1、下列各图中,能作为的图象的是( )
A B C D
2、已知函数分别由下表给出:
1 2 3
1 3 1
1 2 3
3 2 1
则=__________,满足的的值是_______________.
一个面积为100的等腰梯形,上底长为,下底长为上底长的3倍,把它的高表示成的式子为( )
B. C. D.
某商场新进了10台彩电,每台售价3000元,试求出售出彩电数量x(台)与新进彩电销售总额y(元)之间的函数关系,分别用列表法、图像法、解析法表示出来。
5、求下列函数的解析式:
已知;(代入法)
已知f(x)是一次函数,且满足3f(x+1)-2f(x-1)=2x+17,求函数f(x)的解析式。(待定系数法)
已知f(2x+1)=3x-2,求函数f(x)的解析式。(配凑法)
已知;(换元法)
已知.(消去法)
四、课后作业
1、函数y = f (x) 的图象向左平移a(a>0)个单位,再向上平移b(b>0)个单位,所得图象的函数解析式是( )
A.y=f(x-a)+b B.y=f(x+a)-b C.y=f(x-a)-b D.y=f(x+a)+b
2、 一种产品的成本原来是a元,在今后m年内,计划使成本平均每年比上一年降低p%,成本y是经过年数x的函数(0<x<m),其关系式为( )
A.y=a(1+p%)x(0<x<m) B.y=a(1-p%)x(0<x<m)
C.y=a(p%)x(0<x<m) D.y=a-(p%)x(0<x<m)
3、( )
4、 已知函数y=f(x)的定义域为R,f(x-2)=f(3-x),则下列各式中与f(-1)相等的是( )
A.f(1) B.f(0) C.f(2) D.f(-2)
5、已知函数f(x)=3x-4的值域为[-1,5],则f(x)的定义域为______.
6、函数y=-2x+3(-2≤x<4)的值域为______.
7、已知函数f(x)满足,求函数f(x)的解析式。
8、已知,求函数f(x)的解析式。
9、已知,求函数f(x)的解析式。
10、已知,求函数f(x)的解析式。
11、已知f (x+1)=,求f (x)的解析式.
12、已知f (x)是二次函数,且,求f (x).
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
