全等三角形的判定4[上学期]
文档属性
| 名称 | 全等三角形的判定4[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 331.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-03-05 00:00:00 | ||
图片预览







文档简介
课件20张PPT。13.2三角形全等的条件⑷AAS学习目标
1、通过动手实践,自主探索,进一步掌握三角形全等的条件。
2、探索出全等三角形的条件AAS,结合图形能准确表述三角形全等。
3、能运用“角角边”的方法证明三角形全等。作业布置评价小结巩固练习讲授新课复习
教学过程 三边对应相等的两个
三角形全等。边边边:有两边和它们夹角对应
相等的两个三角形全等。边角边:有两角和它们夹边对应
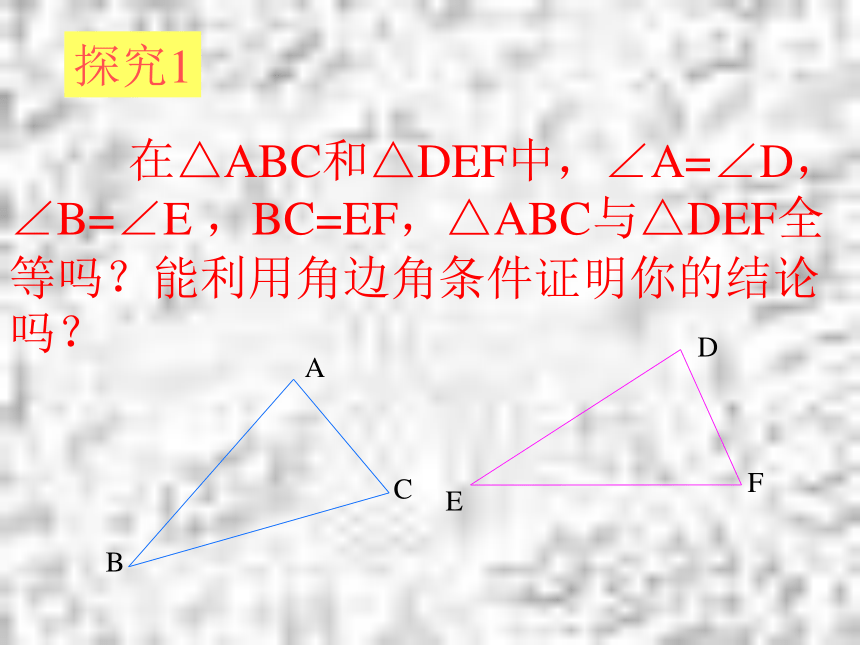
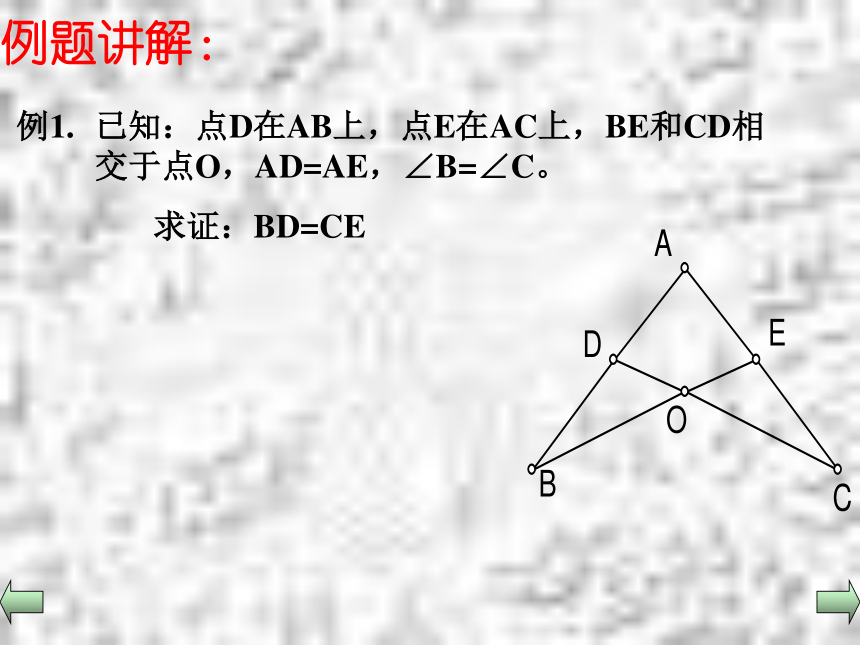
相等的两个三角形全等角边角: 在△ABC和△DEF中,∠A=∠D, ∠B=∠E ,BC=EF,△ABC与△DEF全等吗?能利用角边角条件证明你的结论吗?探究1例题讲解:例题讲解:例1.已知:点D在AB上,点E在AC上,BE和CD相交于
点O,AD=AE,∠B=∠C。
求证:BD=CE 巩固练习如图,∠1=∠2,∠D=∠C
求证:AC=AD证明:在△——和△——中
——( )
—— ( )
—— (公共边)
∴△—— ≌ △——( )
∴—— (全等三角形对应边相等) 六.评价1.错例辨析
若△ABC的∠B=∠C,△A’B’C’的∠B’=∠C’,且BC=B’C’,
那么△ABC与△A’B’C’全等吗?为什么?3.如图,已知∠1=∠2,∠3=∠4,BD=CE
求证:AB=AC(1)学习了角角边。
(2)由实践证明角角边是真命题。
(3)注意角角边中的条件。小结探究2三角对应相等的的两个
三角形全等吗?小结三角形全等的判定方法。知识应用1.如图,要测量河两岸相对的两点A,B
的距离,可以在AB的垂线BF上取两点
C,D,使BC=CD,再定出BF的垂线
DE,使A, C,E在一条直线上,这时
测得DE的长就是AB的长。为什么?2.如图,AB⊥BC,AD⊥DC,
∠1=∠2。
求证AB=AD。1.你能总结出我们学过哪些判定三角形
全等的方法吗?小结2.要根据题意选择适当的方法。3.证明线段或角相等,就是证明它们所
在的两个三角形全等。布置作业P104 习题13.2 5、 6、 11、12.
1、通过动手实践,自主探索,进一步掌握三角形全等的条件。
2、探索出全等三角形的条件AAS,结合图形能准确表述三角形全等。
3、能运用“角角边”的方法证明三角形全等。作业布置评价小结巩固练习讲授新课复习
教学过程 三边对应相等的两个
三角形全等。边边边:有两边和它们夹角对应
相等的两个三角形全等。边角边:有两角和它们夹边对应
相等的两个三角形全等角边角: 在△ABC和△DEF中,∠A=∠D, ∠B=∠E ,BC=EF,△ABC与△DEF全等吗?能利用角边角条件证明你的结论吗?探究1例题讲解:例题讲解:例1.已知:点D在AB上,点E在AC上,BE和CD相交于
点O,AD=AE,∠B=∠C。
求证:BD=CE 巩固练习如图,∠1=∠2,∠D=∠C
求证:AC=AD证明:在△——和△——中
——( )
—— ( )
—— (公共边)
∴△—— ≌ △——( )
∴—— (全等三角形对应边相等) 六.评价1.错例辨析
若△ABC的∠B=∠C,△A’B’C’的∠B’=∠C’,且BC=B’C’,
那么△ABC与△A’B’C’全等吗?为什么?3.如图,已知∠1=∠2,∠3=∠4,BD=CE
求证:AB=AC(1)学习了角角边。
(2)由实践证明角角边是真命题。
(3)注意角角边中的条件。小结探究2三角对应相等的的两个
三角形全等吗?小结三角形全等的判定方法。知识应用1.如图,要测量河两岸相对的两点A,B
的距离,可以在AB的垂线BF上取两点
C,D,使BC=CD,再定出BF的垂线
DE,使A, C,E在一条直线上,这时
测得DE的长就是AB的长。为什么?2.如图,AB⊥BC,AD⊥DC,
∠1=∠2。
求证AB=AD。1.你能总结出我们学过哪些判定三角形
全等的方法吗?小结2.要根据题意选择适当的方法。3.证明线段或角相等,就是证明它们所
在的两个三角形全等。布置作业P104 习题13.2 5、 6、 11、12.
