人教版九年级上册 第22章二次函数复习课件(共60张PPT)
文档属性
| 名称 | 人教版九年级上册 第22章二次函数复习课件(共60张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-19 12:01:52 | ||
图片预览





文档简介
(共60张PPT)
1
人教版九年级数学上册
第二十二章 二次函数
复习课
知识点复习
1.进一步巩固二次函数的概念、图象和性质,能根据解析式判断二次函数的开口方向、对称轴、顶点坐标、增减性等.
2. 熟练应用二次函数各项系数与图象之间的关系解决二次函数的有关问题.
3. 能应用二次函数与一元二次方程之间的关系解决有关的函数和方程问题,会用待定系数法求二次函数解析式.
4.熟练应用二次函数的有关知识解决实际问题,体会其中的数学建模思想.
2
复习目标
重点:二次函数解析式的求法、二次函数的图象及性质.
难点:应用二次函数知识解决有关的实际问题.
3
重点难点
4
情景引入
马小虎当“工程师”(2)
爸爸马大虎要给家里装一扇新窗户,新窗户要用长8米的铝合金做窗框(如图),爸爸想让透光面积最大,怎么做呢 马小虎看出了爸爸的心思,说:“我来设计吧!”不一会,马小虎设计出了符合要求的施工方案,你知道他是怎么做的吗
5
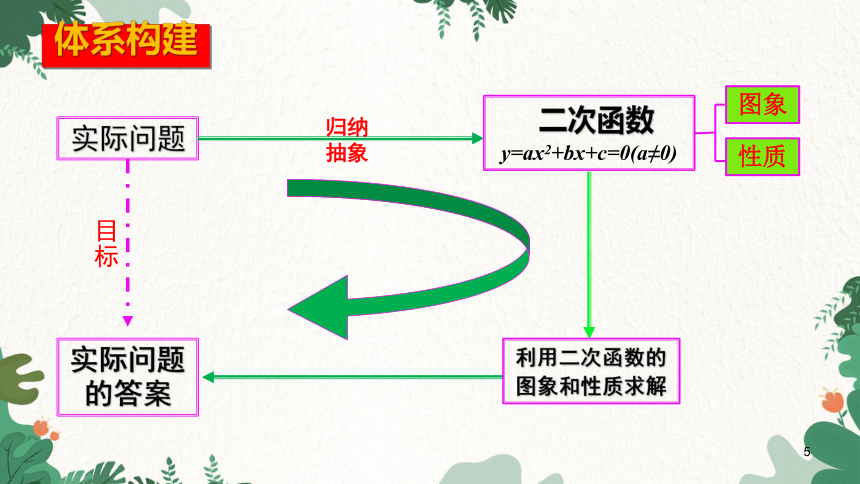
体系构建
实际问题
归纳
抽象
二次函数
y=ax2+bx+c=0(a≠0)
实际问题的答案
图象
利用二次函数的图象和性质求解
性质
目标
6
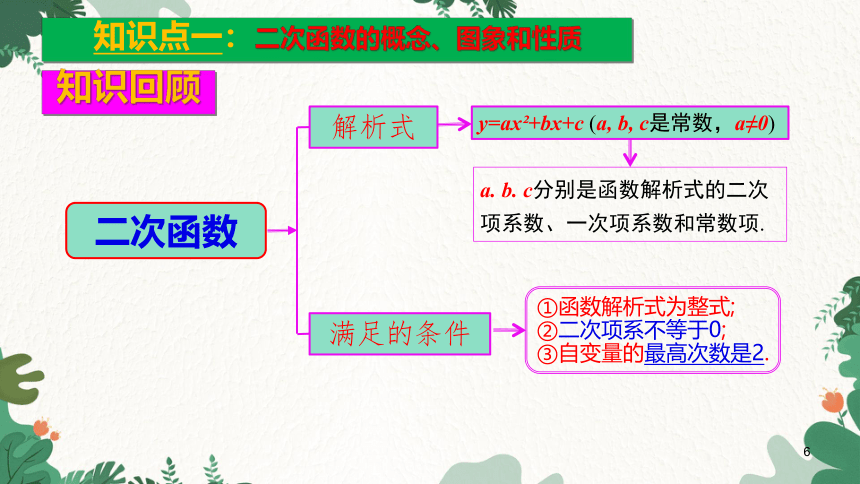
知识回顾
知识点一:二次函数的概念、图象和性质
二次函数
解析式
满足的条件
y=ax +bx+c (a, b, c是常数,a≠0)
a. b. c分别是函数解析式的二次项系数、一次项系数和常数项.
①函数解析式为整式;
②二次项系不等于0;
③自变量的最高次数是2.
7
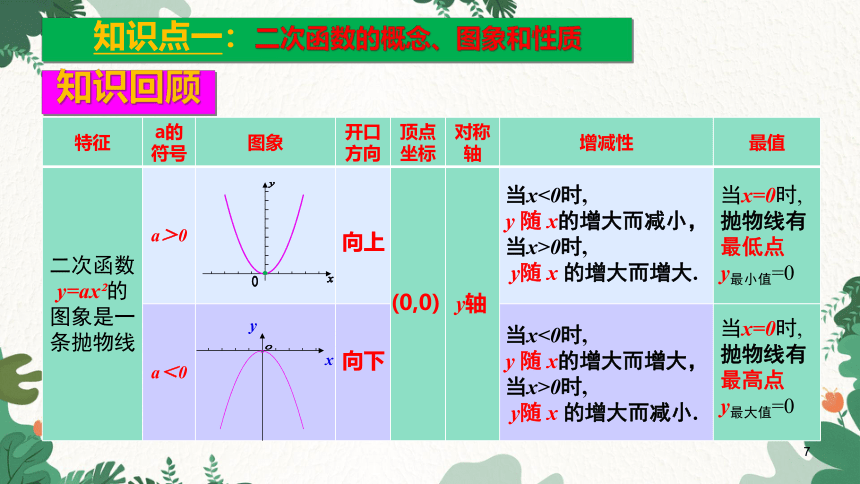
知识回顾
知识点一:二次函数的概念、图象和性质
特征 a的 符号 图象 开口方向 顶点坐标 对称轴 增减性 最值
二次函数y=ax 的图象是一条抛物线 a>0
a<0
x
y
O
O
y
x
向上
向下
(0,0)
y轴
当x<0时,
y 随 x的增大而减小,
当x>0时,
y随 x 的增大而增大.
当x<0时,
y 随 x的增大而增大,当x>0时,
y随 x 的增大而减小.
当x=0时,
抛物线有最低点
y最小值=0
当x=0时,
抛物线有最高点
y最大值=0
8
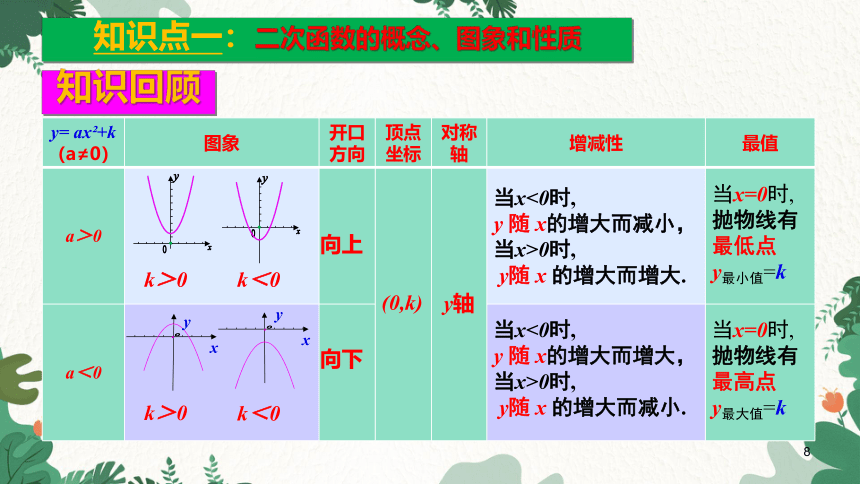
知识回顾
知识点一:二次函数的概念、图象和性质
y= ax +k (a≠0) 图象 开口方向 顶点坐标 对称轴 增减性 最值
a>0
a<0
x
y
O
O
y
x
向上
向下
(0,k)
y轴
当x<0时,
y 随 x的增大而减小,
当x>0时,
y随 x 的增大而增大.
当x<0时,
y 随 x的增大而增大,
当x>0时,
y随 x 的增大而减小.
当x=0时,
抛物线有最低点
y最小值=k
当x=0时,
抛物线有最高点
y最大值=k
x
y
O
k>0
k<0
k>0
k<0
O
y
x
9
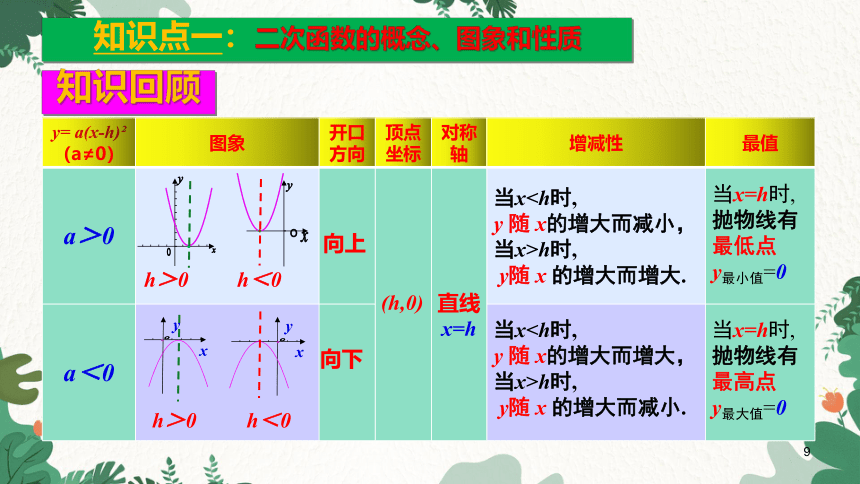
知识回顾
知识点一:二次函数的概念、图象和性质
y= a(x-h) (a≠0) 图象 开口方向 顶点坐标 对称轴 增减性 最值
a>0
a<0
向上
向下
(h,0)
直线x=h
当xy 随 x的增大而减小,
当x>h时,
y随 x 的增大而增大.
当xy 随 x的增大而增大,
当x>h时,
y随 x 的增大而减小.
当x=h时,
抛物线有最低点
y最小值=0
当x=h时,
抛物线有最高点
y最大值=0
h>0
h<0
h>0
h<0
x
y
O
x
y
O
O
y
x
O
y
x
10
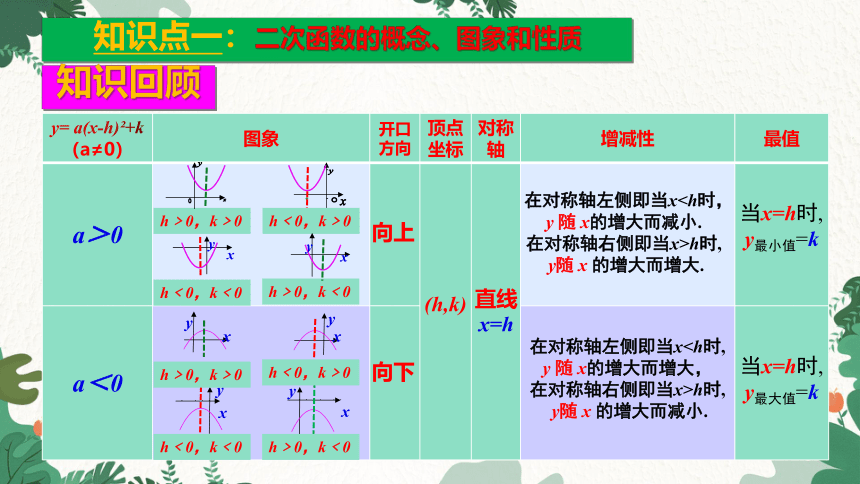
知识回顾
知识点一:二次函数的概念、图象和性质
y= a(x-h) +k (a≠0) 图象 开口方向 顶点坐标 对称轴 增减性 最值
a>0
a<0
向上
向下
(h,k)
直线x=h
在对称轴左侧即当xy 随 x的增大而减小.
在对称轴右侧即当x>h时,
y随 x 的增大而增大.
在对称轴左侧即当xy 随 x的增大而增大,
在对称轴右侧即当x>h时,
y随 x 的增大而减小.
当x=h时,
y最小值=k
当x=h时,
y最大值=k
h﹥0,k﹥0
x
y
O
x
y
O
y
x
y
x
h﹤0,k﹥0
h﹤0,k﹤0
h﹥0,k﹤0
h﹥0,k﹥0
h﹤0,k﹥0
h﹤0,k﹤0
h﹥0,k﹤0
x
y
x
y
y
x
y
x
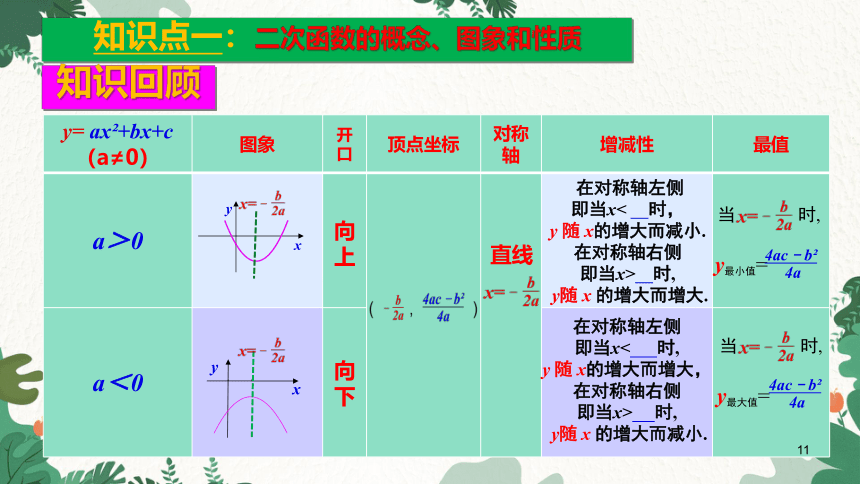
y= ax +bx+c (a≠0) 图象 开口 顶点坐标 对称轴 增减性 最值
a>0
a<0
向上
向下
直线
在对称轴左侧
即当x< 时,
y 随 x的增大而减小.
在对称轴右侧
即当x> 时,
y随 x 的增大而增大.
在对称轴左侧
即当x< 时,
y 随 x的增大而增大,
在对称轴右侧
即当x> 时,
y随 x 的增大而减小.
当 时,
y最小值=
11
x
y
y
x
当 时,
y最大值=
4ac﹣b
4a
4ac﹣b
4a
知识回顾
知识点一:二次函数的概念、图象和性质
12
巩固练习
知识点一:二次函数的概念、图象和性质
1.已知 a< -1,点(a- 1,y1),(a,y2),(a+1,y3)都在函数y=x2的图象上,则( )
A.y12.已知二次函数 y=(k-1)xk -3k+2的图象开口向上,则 k= .
若开口向上,则 k= .
C
3
0
3.抛物线 y=3x2与直线 y=kx+4的交点为(2,b),则k = ,
b= .
4
12
13
巩固练习
知识点一:二次函数的概念、图象和性质
4.已知a≠0,在同一直角坐标系中,函数 y=ax与 y=ax2 的图象可能是( )
A. B. C. D.
x
y
O
x
y
O
-1
O
y
x
O
y
x
-1
1
D
14
巩固练习
知识点一:二次函数的概念、图象和性质
5.下列关于抛物线 y= - x2 与 y= - x2+1 的叙述:
①开口都向下; ②都关于 y 轴对称;
③当 x<0 时, y 随 x 的增大而增大;④顶点坐标相同.
其中正确的个数为( ). A.1 B.2 C.3 D.4
6.(易错题)已知点A(x1,y1) ,B(x2,y2)是二次函数y=ax2 +2(a<0)
图像上的两点,若x1>x2>0,则y1,y2的大小关系是 ;
(易错提示:画出草图,借助图形的直观性可避免出现失误)
C
y1 < y2
15
巩固练习
知识点一:二次函数的概念、图象和性质
7.在同一直角坐标系中,一次函数 y= -mx+n 与二次函数
y= x2+m 的图象可能是( ).
D
A. B. C. D.
O
y
x
O
y
x
O
y
x
O
y
x
16
巩固练习
知识点一:二次函数的概念、图象和性质
8.已知抛物线 y=3(x+2)2 与 y=3(x-2)2,下列说法错误的是( )
A.形状相同,开口方向相反 B.对称轴关于y轴对称
C.顶点关于y轴对称 D.图象关于y轴对称
9.已知点(﹣1, y1), (﹣ , y2), ( , y3) 在函数 y=2(x﹣1) 的图象上,则 y1 , y2 , y3关的大小关系是 .
(用“<”连接).
A
y3<y1<y2
17
巩固练习
知识点一:二次函数的概念、图象和性质
10.已知二次函数 y= -(x+3)2-4的图象的对称轴为直线l,点M是直线l上一点,则点M的坐标可能是( )
A.(3,0) B.(-4,3) C.(4,-3) D.(-3,1)
11.已知二次函数 y=a(x-2)2+c(a>0),当自变量x分别取1,3,0时,对
应的函数值分别为 y1 , y2 , y3 ,则 y1 , y2 , y3 的大小关系正确的
是( )
A. y3D
B
18
巩固练习
知识点一:二次函数的概念、图象和性质
12.如图在同一直角坐标系中,一次函数 y=ax+a+b 与二次函数y= a(x+1)2+b 的图象可能是( ).
A. B. C. D.
O
y
x
O
y
x
C
O
y
x
O
y
x
19
13.对于二次函数y= - x +x-4,下列说法正确的是( )
A.当x>0时,y随x的增大而增大 B.当x=2时,y有最大值-3
C.图象的顶点坐标为(-2,-7 ) D.图象与x轴有两个交点
14.点P (-1,y1),P (3,y2),P (5,y3)均在二次函数y= -x2+2x+c的图象上,则y1,y2,y3的大小关系是( )
A .y3>y2>y1 B. y3>y1=y2 C.y1>y2>y3 D.y1=y2>y3
1
4
B
D
巩固练习
知识点一:二次函数的概念、图象和性质
20
20
字母的符号 图象特征
a a>0
a<0
b b=0
ab>0 (a , b同号)
ab<0 (a , b异号)
c c=0
c>0
c<o
开口向上
开口向下
对称轴为y轴
对称轴在y轴左侧(左同)
对称轴在y轴右侧(右异)
图象过原点
与y轴正半轴相交
与y轴负半轴相交
知识回顾
知识点一:二次函数的概念、图象和性质
利用二次函数图象的位置判断a、b、c的取值范围
21
对于二次函数 y=ax2+bx+c,
当 x=1时, y=a+b+c.此时,
若 y>0,则a+b+c>0;若 y=0,则a+b+c=0;若 y<0,则a+b+c<0.
当 x=﹣1时, y=a-b+c此时,
若 y>0,则a-b+c>0;若 y=0,则a-b+c=0;若 y<0,则a-b+c<0.
知识回顾
知识点一:二次函数的概念、图象和性质
22
巩固练习
知识点一:二次函数的概念、图象和性质
1.二次函数y=ax2+bx+c的图象如图所示给出下列结论:① b<0; ② c>0; ③ a+b+c>0; ④ 4a+2b+c<0.其中正确的个数是( ) A.1 B.2 C.3 D.4
x
y
0
1
2
-1
C
23
2、函数 y=ax+b与 y=ax2+bx+c(a≠0)在同一坐标系内的图象可能是( )
A. B. C. D.
O
y
x
O
y
x
O
y
x
O
y
x
B
巩固练习
知识点一:二次函数的概念、图象和性质
24
3.二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线 x=1,则下列四个结论错误的是( )
A.c>0 B.2a+b=0
C. abc<0 D. a-b+c>0
x
y
0
1
2
-1
D
巩固练习
知识点一:二次函数的概念、图象和性质
25
知识回顾
知识点二:抛物线的平移
向下平移 1个单位
向上平移 1个单位
向左平移
1个单位
向右平移
1个单位
上加下减
左加右减
26
知识回顾
知识点二:抛物线的平移
上加下减常数项,
左加右减自变量.
函数平移有规律,
上下左右显神方.
27
知识回顾
知识点二:抛物线的平移
向右(h>0)或向左(h<0)平移|h|个单位长度
向右(h>0)或向左(h<0)平移|h|个单位长度
向上(k﹥0)或向下(k﹤0)平移|k|个单位长度
向上(k﹥0)或向下(k﹤0)平移|k|个单位长度
向右(h>0)或向左(h<0)平移|h|个单位长度
再向上(k>0)或向下(k<0)平移|h|个单位长度
28
巩固练习
知识点二:抛物线的平移
1.已知 y=a(x-h)2+k是由抛物线 y= -2x2向上平移2个单位长度,
再向右平移1个单位长度得到的,则a= ,h= , k= ;
-2
1
2
2.将抛物线 y=x2 向上平移1个单位,则平移后的抛物线的解析式为 .
y=x2+1
3.在同一平面直角坐标系中,不可能由函数 y=2x2+1 的图象通过上下平移变换得到的函数是( )
A.y=2x2- 1 B. y=2x2 C.y=2x2+7 D.y= x2+1
D
29
巩固练习
知识点二:抛物线的平移
4.对于抛物线 y= (x+2) +3,给出下列结论:
①抛物线 y= (x+2)2+3可由抛物线y= x 先向左平移2个单位长度,再向上平移3个单位长度得到;
②对称轴为直线 x=2;
③顶点坐标为(-2,3);
④当 x>-2时,y随x的增大而增大.其中正确结论的个数为( )
A.1 B.2 C.3 D.4
C
抛物线 y= a(x-h) +k ,与抛物线 y = ax 有形状相同位置不同,可以根据顶点位置确定平移方式.
30
知识回顾
知识点三:二次函数解析式的确定
形式 内容 适用条件
一般式
顶点式
交点式
y= ax2 +bx+c,(a,b,c为常数,a≠0)
y=a(x -h)2+k(a,h,k为常数,a≠0),抛物线的顶点坐标为(h,k)
y=a(x - x1)(x- x2)(a,x1,x2为常数,a≠0),其中是抛物线与x轴两个交点的横坐标
已知抛物线上任意三点坐标时,通常设函数的解析式为一般式, 然后列出关于a,b,c
当已知抛物线的顶点坐标或对称轴和最值时,通常设函数的解析式为 项点式,然后代入另一点的坐标,解关于a的一元一次方程
当已知抛物线与x轴的两交点坐标或一个交点的坐标和对称轴时,通常设函数的解析式为交点式,然后代入另一点的坐标,解关于a的一元一次方程
31
知识回顾
知识点三:二次函数解析式的确定
二次函数的解析式
顶点式:y=a(x -h)2+k (a≠0)
交点式:y=a(x - x1)(x- x2)(a≠0)
一般式:y= ax +bx+c(a≠0).
需知:抛物线上不在同一直线上的三点.
需知:顶点及异于顶点的另一点.
需知:与x轴的交点及异于交点的另一端
32
1.若二次函数 y=ax +bx+c,则由表格中的信息可知y与x之间的函数解析式是( )
A.y=x2-4x+3 B. y=x -3x+4 C.y=x - 3x+ 3 D.y=x -4x +8
x -1 0 1
ax 1
ax +bx+c 8 3
知识点三:二次函数解析式的确定
巩固练习
33
知识点三:二次函数解析式的确定
2.二次函数 y=x2 +bx+c 的图象经过点(4,3),(3,0).
(1)求b、c的值;
(2)求该二次函数图象的顶点坐标和对称轴.
巩固练习
34
巩固练习
知识点三:二次函数解析式的确定
3.若二次函数y= ax2 +bx+c的顶点是A(2,1),且经过点B(1,0),求这个二次函数的解析式.
解:根据题意设二次函数解析式为y=a(x -2)2+1.
把点B(1,0)代入得:a(1﹣2)2+1=0
解得:a=﹣1
∴二次函数的解析式是y=﹣(x -2)2+1.
35
知识点三:二次函数解析式的确定
巩固练习
4.二次函数 y=x +px+q的最小值是4,且当 x=2时,y=5,则p,q的值为( ).
A.p=-2,q=15 B.p=-2,q=5或 p=-6,q=13
C.p=-6,q=13 D.p=2,q=-5或 p=6,q=-13
5.若二次函数的图象的顶点坐标为(2,﹣1),且抛物线过(0,3),则二次函数的解析式是( ).
A.y=-(x-2) -1 B.y=- (x-2) - 1 C.y=(x-2)2-1 D.y= (x-2) -1
1
2
1
2
36
知识点三:二次函数解析式的确定
巩固练习
6.已知二次函数 y=x +bx+c 的图像经过点(-1,0),(4,0),
则c= .
7.已知抛物线过点A(2,0),B(-1,0),与y轴交于点C,且OC=2,则这条抛物线的解析式为( ).
A.y=x -x-2 B.y= -x +x+2
C.y=x -x-2或 y=-x +x+2 D.y= -x -x-2或 y= x +x+2
-4
C
37
知识回顾
知识点四:二次函数与一元二次方程
二次函数 y=ax2 +bx+c,当 y=0时,得到一元二次方程 ax2 +bx+c=0,
所以抛物线 y=ax2 +bx+c与x轴的公共点的横坐标就是一元二次方程 ax2 +bx+c=0的根.
38
知识回顾
知识点四:二次函数与一元二次方程
一般地,从二次函数 y=ax2+bx+c 的图象可知:
(2)二次函数的图象与x轴的位置关系有三种:
没有公共点,有一个公共点,有两个公共点;
这对应着一元二次方程根的三种情况:
没有实数根,有两个相等的实数根,有两个不等的实数根
(1)如果抛物线y=ax2+bx+c 与x轴有公共点,公共点的横坐标是x0,那么当x =x0时,函数的值是0,因此x = x0 就是方程 ax2+bx+c=0 的一个根.
39
巩固练习
知识点四:二次函数与一元二次方程
1.二次函数 y=x2- 2x- 3 的图象与 x 轴的两个交点之间的距离为 .
2.若一元二次方程 ax2+bx+c=0 的两根为x1= -3,x2=1,则二次函数 y= ax2+bx+c 的图象的对称轴是直线 .
3.将拋物线 y=x2-1向下平移8个单位长度后与x轴的两个交点之间的距离为( )
A.4 B.6 C.8 D.10
4
x= -1
B
40
巩固练习
知识点四:二次函数与一元二次方程
4.已知抛物线 y=kx +2(k+1)x+k+1 开口向下,且与x轴有两个交点,则k的取值范围是( ).
A.-1-1
5.已知二次函数 y= -x2+2x+m的部分
图象如图,则关于x的一元二次方程
-x2 +2x+m=0的解为 .
A
x1=3,x2= -1
当已知抛物线与x轴的一个交点的横坐标和对称轴时,可根据轴对称的性质求出抛物线与x轴另一个交点的横坐标,从而求得对应一元二次方程的根.
41
巩固练习
知识点四:二次函数与一元二次方程
6.已知拋物线 y=x2-2x -1与x轴的一个交点为(m ,0).则代数式m2-2m +2018的值为( )
A.2015 B.2016 C.2017 D.2018
7.若关于x的一元二次方程 a(x+m)2 -3=0的两个实数根分别为x1= -1,x2=3,则抛物线 y=a(x+m)2-3与x轴的交点坐标
为 .
D
(3,0),( -1,0)
42
知识回顾
知识点五:二次函数的应用
二次函数解决图形面积问题
求有关几何图形面积的最值问题,往往可转化成求二次函数的最值问题,需要借助几何图形,建立变量之间的二次函数关系,配方将函数解析式转化为顶点式,然后利用二次函数的最值解决问题,要特别注意自变量的取值范围.
43
1.如图,有长为24 m的篱笆,一面利用墙
(墙的最大可用长度为9 m)围成中间隔有一
道篱笆的长方形养鸡场.设养鸡场的长BC为 xm,面积为 ym2.
(1)求 y与x的函数关系,并写出 x 的取值范围.
(2)当长方形的长、宽各为多少时,养鸡场的面积最大,最大的面积是多少
9
墙
B
A
C
D
巩固练习
知识点五:二次函数的应用
二次函数解决图形面积问题
44
2、如图,某小区准备用80m长的篱笆围成一块矩形花圃ABCD,为了节省篱笆,一边利用足够长的墙,另外三边用篱笆围着,再用两段篱笆EF与GH将矩形ABCD分割成①②③三块矩形区域,而且这三块矩形区域的面积相等,设BC的
长度为x m,矩形区域ABCD的面积为y m2.
(1)求y与x 之间的函数关系式,并注明
自变量x 的取值范围;
(2)求x 为何值时,y有最大值 最大值是多少
墙
A
B
C
D
E
F
G
H
区域①
区域②
区域③
巩固练习
知识点五:二次函数的应用
二次函数解决图形面积问题
45
知识回顾
知识点五:二次函数的应用
二次函数求商品的最大利润
在市场销售的利润问题中的等量关系:
总利润=销售总收入﹣总成本;
销售总收入=销售单价×销售量;
总成本=销售量×成本单价.
总利润=单利润×销售量;
46
巩固练习
知识点五:二次函数的应用
二次函数求商品的最大利润
1.某商品的销售利润 W(元)与销售单价x(元)满足函数关系式W= -x2+10x-16,则获得的利润( )
A.最大值为9元 B.最小值为31元
C.最大值为31元 D.最小值为9元
2.已知某商店所销售的毛绒玩具每件的进价为30元,在某段时间内若以每件x元(30≤ x ≤50,且 x 为整数)出售,可卖出(50-x)件,若要使该商店销售该玩具的利润最大,每件的售价为( ).
A
A.35元 B.40元 C.45元 D.48元
B
47
巩固练习
知识点五:二次函数的应用
二次函数求商品的最大利润
3.【2018年安徽省12分】小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元,调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1,W2(单位:元)
(1)用含x的代数式分别表示W1,W2;
(2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少
48
知识回顾
知识点五:二次函数的应用
拱桥类抛物线问题
利用二次函数解决抛物线形的建筑物问题的方法
需要先建立合适的坐标系,一般选择顶点作为原点或选择对称轴作为y轴,然后确定某些点的坐标,再用待定系数法求出函数解析式,最后利用二次函数的图象和性质解题.
49
巩固练习
知识点五:二次函数的应用
拱桥类抛物线问题
1.如图所示,某河面上有一座抛物线形拱桥,
桥下水面在正常水位 AB时,宽为20m,若水
位上升3m,水面就会达到警戒线CD,这时水面宽度为10m.
(1)建立适当的平面直角坐标系并求出抛物线的解析式;
解: (1)以抛物线的顶点为原点,抛物线的对称轴为y轴,建立如图所示的平面直角坐标系.
25a=m,
100a=m-3,
设所求抛物线的解析式为 y=ax2,点D的坐标为D(5,m),则B(10,m-3).
由抛物线经过点D和点B,可得:
a= - ,
m= -1,
∴
20m
10m
x
y
0
∟
∟
50
巩固练习
知识点五:二次函数的应用
拱桥类抛物线问题
1.(2)若洪水到来时,水位以每小时0.2 m的
速度上升从警戒线开始,再持续多少小时就
能到达拱桥的拱顶
20m
10m
20m
10m
x
y
0
∟
∟
51
知识点五:二次函数的应用
2.如图是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景灯.若把拱桥的截面图放
在平面直角坐标系中,则两盏景灯之
间的水平距离是( )m.
A.3 B.4 C.5 D.6
C
巩固练习
拱桥类抛物线问题
52
知识点五:二次函数的应用
巩固练习
抛物线型问题
3.
53
M
y
x
0
A
B
C
N
a
h
其中 a= xC ﹣xB
h= yA ﹣yN
∴S ABC= ah
1
2
知识回顾
抛物线中的三角形的面积
知识点五:二次函数的应用
54
知识回顾
抛物线中的三角形的面积
知识点五:二次函数的应用
利用二次函数的图象和性质解决动态问题的方法
求解动态问题时,常要以“静”制“动”,找出图形在变化过程中不变的量或遵循的数量关系,从而构建函数关系式求解.若在运动过程中,随着自变量的改变,函数关系或图形也发生改变,则需要针对函数关系或图形变化的情况分类讨论.
求解动态问题时,依据图形分析变量间的关系是解题的关键.
55
巩固练习
1.如图,抛物线 y= - x2+3与x轴交于A,B两点,与直线 y= - x+b
相交于B,C两点,连接A,C两点.
(1)写出直线BC的解析式.
(2)求 ABC的面积 .
O
y
x
B
C
A
抛物线中的三角形的面积
知识点五:二次函数的应用
56
巩固练习
抛物线中的三角形的面积
知识点五:二次函数的应用
2.【2016年安徽省12分】如图,二次函数
y=ax +bx的图象经过点A(2,4)与B(6,0).
(1)求a、b的值;
(2)点C是该二次函数图象上A,B两点
之间的一动点,横坐标为 x (2<x<6).写出四边形OACB的面积S关于点C的横坐标 x 的函数表达式,并求S的最大值.
1
2
1
3
-1
y
x
0
4
5
6
7
2
3
4
5
A
B
C
M
57
巩固练习
抛物线中的三角形的面积
知识点五:二次函数的应用
3.如图(1)抛物线 y= -x2+bx+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于C点,点P是抛物线上在要一象限内的一个动点,且点P的横坐标为t
(1)求抛物线的解析式;
P
y
x
0
A
B
C
-1
3
58
巩固练习
抛物线中的三角形的面积
知识点五:二次函数的应用
(2)如图(2),连接BC,PB.PC.设 PBC的面积为S.
①求S关于t的函数解析式;
②求P点到直线BC的距离的最大值。并求出此时点P的坐标.
P
y
x
0
A
B
C
M
-1
3
3
知识结构图
59
60
对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?
蓦然回首
1
人教版九年级数学上册
第二十二章 二次函数
复习课
知识点复习
1.进一步巩固二次函数的概念、图象和性质,能根据解析式判断二次函数的开口方向、对称轴、顶点坐标、增减性等.
2. 熟练应用二次函数各项系数与图象之间的关系解决二次函数的有关问题.
3. 能应用二次函数与一元二次方程之间的关系解决有关的函数和方程问题,会用待定系数法求二次函数解析式.
4.熟练应用二次函数的有关知识解决实际问题,体会其中的数学建模思想.
2
复习目标
重点:二次函数解析式的求法、二次函数的图象及性质.
难点:应用二次函数知识解决有关的实际问题.
3
重点难点
4
情景引入
马小虎当“工程师”(2)
爸爸马大虎要给家里装一扇新窗户,新窗户要用长8米的铝合金做窗框(如图),爸爸想让透光面积最大,怎么做呢 马小虎看出了爸爸的心思,说:“我来设计吧!”不一会,马小虎设计出了符合要求的施工方案,你知道他是怎么做的吗
5
体系构建
实际问题
归纳
抽象
二次函数
y=ax2+bx+c=0(a≠0)
实际问题的答案
图象
利用二次函数的图象和性质求解
性质
目标
6
知识回顾
知识点一:二次函数的概念、图象和性质
二次函数
解析式
满足的条件
y=ax +bx+c (a, b, c是常数,a≠0)
a. b. c分别是函数解析式的二次项系数、一次项系数和常数项.
①函数解析式为整式;
②二次项系不等于0;
③自变量的最高次数是2.
7
知识回顾
知识点一:二次函数的概念、图象和性质
特征 a的 符号 图象 开口方向 顶点坐标 对称轴 增减性 最值
二次函数y=ax 的图象是一条抛物线 a>0
a<0
x
y
O
O
y
x
向上
向下
(0,0)
y轴
当x<0时,
y 随 x的增大而减小,
当x>0时,
y随 x 的增大而增大.
当x<0时,
y 随 x的增大而增大,当x>0时,
y随 x 的增大而减小.
当x=0时,
抛物线有最低点
y最小值=0
当x=0时,
抛物线有最高点
y最大值=0
8
知识回顾
知识点一:二次函数的概念、图象和性质
y= ax +k (a≠0) 图象 开口方向 顶点坐标 对称轴 增减性 最值
a>0
a<0
x
y
O
O
y
x
向上
向下
(0,k)
y轴
当x<0时,
y 随 x的增大而减小,
当x>0时,
y随 x 的增大而增大.
当x<0时,
y 随 x的增大而增大,
当x>0时,
y随 x 的增大而减小.
当x=0时,
抛物线有最低点
y最小值=k
当x=0时,
抛物线有最高点
y最大值=k
x
y
O
k>0
k<0
k>0
k<0
O
y
x
9
知识回顾
知识点一:二次函数的概念、图象和性质
y= a(x-h) (a≠0) 图象 开口方向 顶点坐标 对称轴 增减性 最值
a>0
a<0
向上
向下
(h,0)
直线x=h
当x
当x>h时,
y随 x 的增大而增大.
当x
当x>h时,
y随 x 的增大而减小.
当x=h时,
抛物线有最低点
y最小值=0
当x=h时,
抛物线有最高点
y最大值=0
h>0
h<0
h>0
h<0
x
y
O
x
y
O
O
y
x
O
y
x
10
知识回顾
知识点一:二次函数的概念、图象和性质
y= a(x-h) +k (a≠0) 图象 开口方向 顶点坐标 对称轴 增减性 最值
a>0
a<0
向上
向下
(h,k)
直线x=h
在对称轴左侧即当x
在对称轴右侧即当x>h时,
y随 x 的增大而增大.
在对称轴左侧即当x
在对称轴右侧即当x>h时,
y随 x 的增大而减小.
当x=h时,
y最小值=k
当x=h时,
y最大值=k
h﹥0,k﹥0
x
y
O
x
y
O
y
x
y
x
h﹤0,k﹥0
h﹤0,k﹤0
h﹥0,k﹤0
h﹥0,k﹥0
h﹤0,k﹥0
h﹤0,k﹤0
h﹥0,k﹤0
x
y
x
y
y
x
y
x
y= ax +bx+c (a≠0) 图象 开口 顶点坐标 对称轴 增减性 最值
a>0
a<0
向上
向下
直线
在对称轴左侧
即当x< 时,
y 随 x的增大而减小.
在对称轴右侧
即当x> 时,
y随 x 的增大而增大.
在对称轴左侧
即当x< 时,
y 随 x的增大而增大,
在对称轴右侧
即当x> 时,
y随 x 的增大而减小.
当 时,
y最小值=
11
x
y
y
x
当 时,
y最大值=
4ac﹣b
4a
4ac﹣b
4a
知识回顾
知识点一:二次函数的概念、图象和性质
12
巩固练习
知识点一:二次函数的概念、图象和性质
1.已知 a< -1,点(a- 1,y1),(a,y2),(a+1,y3)都在函数y=x2的图象上,则( )
A.y1
若开口向上,则 k= .
C
3
0
3.抛物线 y=3x2与直线 y=kx+4的交点为(2,b),则k = ,
b= .
4
12
13
巩固练习
知识点一:二次函数的概念、图象和性质
4.已知a≠0,在同一直角坐标系中,函数 y=ax与 y=ax2 的图象可能是( )
A. B. C. D.
x
y
O
x
y
O
-1
O
y
x
O
y
x
-1
1
D
14
巩固练习
知识点一:二次函数的概念、图象和性质
5.下列关于抛物线 y= - x2 与 y= - x2+1 的叙述:
①开口都向下; ②都关于 y 轴对称;
③当 x<0 时, y 随 x 的增大而增大;④顶点坐标相同.
其中正确的个数为( ). A.1 B.2 C.3 D.4
6.(易错题)已知点A(x1,y1) ,B(x2,y2)是二次函数y=ax2 +2(a<0)
图像上的两点,若x1>x2>0,则y1,y2的大小关系是 ;
(易错提示:画出草图,借助图形的直观性可避免出现失误)
C
y1 < y2
15
巩固练习
知识点一:二次函数的概念、图象和性质
7.在同一直角坐标系中,一次函数 y= -mx+n 与二次函数
y= x2+m 的图象可能是( ).
D
A. B. C. D.
O
y
x
O
y
x
O
y
x
O
y
x
16
巩固练习
知识点一:二次函数的概念、图象和性质
8.已知抛物线 y=3(x+2)2 与 y=3(x-2)2,下列说法错误的是( )
A.形状相同,开口方向相反 B.对称轴关于y轴对称
C.顶点关于y轴对称 D.图象关于y轴对称
9.已知点(﹣1, y1), (﹣ , y2), ( , y3) 在函数 y=2(x﹣1) 的图象上,则 y1 , y2 , y3关的大小关系是 .
(用“<”连接).
A
y3<y1<y2
17
巩固练习
知识点一:二次函数的概念、图象和性质
10.已知二次函数 y= -(x+3)2-4的图象的对称轴为直线l,点M是直线l上一点,则点M的坐标可能是( )
A.(3,0) B.(-4,3) C.(4,-3) D.(-3,1)
11.已知二次函数 y=a(x-2)2+c(a>0),当自变量x分别取1,3,0时,对
应的函数值分别为 y1 , y2 , y3 ,则 y1 , y2 , y3 的大小关系正确的
是( )
A. y3
B
18
巩固练习
知识点一:二次函数的概念、图象和性质
12.如图在同一直角坐标系中,一次函数 y=ax+a+b 与二次函数y= a(x+1)2+b 的图象可能是( ).
A. B. C. D.
O
y
x
O
y
x
C
O
y
x
O
y
x
19
13.对于二次函数y= - x +x-4,下列说法正确的是( )
A.当x>0时,y随x的增大而增大 B.当x=2时,y有最大值-3
C.图象的顶点坐标为(-2,-7 ) D.图象与x轴有两个交点
14.点P (-1,y1),P (3,y2),P (5,y3)均在二次函数y= -x2+2x+c的图象上,则y1,y2,y3的大小关系是( )
A .y3>y2>y1 B. y3>y1=y2 C.y1>y2>y3 D.y1=y2>y3
1
4
B
D
巩固练习
知识点一:二次函数的概念、图象和性质
20
20
字母的符号 图象特征
a a>0
a<0
b b=0
ab>0 (a , b同号)
ab<0 (a , b异号)
c c=0
c>0
c<o
开口向上
开口向下
对称轴为y轴
对称轴在y轴左侧(左同)
对称轴在y轴右侧(右异)
图象过原点
与y轴正半轴相交
与y轴负半轴相交
知识回顾
知识点一:二次函数的概念、图象和性质
利用二次函数图象的位置判断a、b、c的取值范围
21
对于二次函数 y=ax2+bx+c,
当 x=1时, y=a+b+c.此时,
若 y>0,则a+b+c>0;若 y=0,则a+b+c=0;若 y<0,则a+b+c<0.
当 x=﹣1时, y=a-b+c此时,
若 y>0,则a-b+c>0;若 y=0,则a-b+c=0;若 y<0,则a-b+c<0.
知识回顾
知识点一:二次函数的概念、图象和性质
22
巩固练习
知识点一:二次函数的概念、图象和性质
1.二次函数y=ax2+bx+c的图象如图所示给出下列结论:① b<0; ② c>0; ③ a+b+c>0; ④ 4a+2b+c<0.其中正确的个数是( ) A.1 B.2 C.3 D.4
x
y
0
1
2
-1
C
23
2、函数 y=ax+b与 y=ax2+bx+c(a≠0)在同一坐标系内的图象可能是( )
A. B. C. D.
O
y
x
O
y
x
O
y
x
O
y
x
B
巩固练习
知识点一:二次函数的概念、图象和性质
24
3.二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线 x=1,则下列四个结论错误的是( )
A.c>0 B.2a+b=0
C. abc<0 D. a-b+c>0
x
y
0
1
2
-1
D
巩固练习
知识点一:二次函数的概念、图象和性质
25
知识回顾
知识点二:抛物线的平移
向下平移 1个单位
向上平移 1个单位
向左平移
1个单位
向右平移
1个单位
上加下减
左加右减
26
知识回顾
知识点二:抛物线的平移
上加下减常数项,
左加右减自变量.
函数平移有规律,
上下左右显神方.
27
知识回顾
知识点二:抛物线的平移
向右(h>0)或向左(h<0)平移|h|个单位长度
向右(h>0)或向左(h<0)平移|h|个单位长度
向上(k﹥0)或向下(k﹤0)平移|k|个单位长度
向上(k﹥0)或向下(k﹤0)平移|k|个单位长度
向右(h>0)或向左(h<0)平移|h|个单位长度
再向上(k>0)或向下(k<0)平移|h|个单位长度
28
巩固练习
知识点二:抛物线的平移
1.已知 y=a(x-h)2+k是由抛物线 y= -2x2向上平移2个单位长度,
再向右平移1个单位长度得到的,则a= ,h= , k= ;
-2
1
2
2.将抛物线 y=x2 向上平移1个单位,则平移后的抛物线的解析式为 .
y=x2+1
3.在同一平面直角坐标系中,不可能由函数 y=2x2+1 的图象通过上下平移变换得到的函数是( )
A.y=2x2- 1 B. y=2x2 C.y=2x2+7 D.y= x2+1
D
29
巩固练习
知识点二:抛物线的平移
4.对于抛物线 y= (x+2) +3,给出下列结论:
①抛物线 y= (x+2)2+3可由抛物线y= x 先向左平移2个单位长度,再向上平移3个单位长度得到;
②对称轴为直线 x=2;
③顶点坐标为(-2,3);
④当 x>-2时,y随x的增大而增大.其中正确结论的个数为( )
A.1 B.2 C.3 D.4
C
抛物线 y= a(x-h) +k ,与抛物线 y = ax 有形状相同位置不同,可以根据顶点位置确定平移方式.
30
知识回顾
知识点三:二次函数解析式的确定
形式 内容 适用条件
一般式
顶点式
交点式
y= ax2 +bx+c,(a,b,c为常数,a≠0)
y=a(x -h)2+k(a,h,k为常数,a≠0),抛物线的顶点坐标为(h,k)
y=a(x - x1)(x- x2)(a,x1,x2为常数,a≠0),其中是抛物线与x轴两个交点的横坐标
已知抛物线上任意三点坐标时,通常设函数的解析式为一般式, 然后列出关于a,b,c
当已知抛物线的顶点坐标或对称轴和最值时,通常设函数的解析式为 项点式,然后代入另一点的坐标,解关于a的一元一次方程
当已知抛物线与x轴的两交点坐标或一个交点的坐标和对称轴时,通常设函数的解析式为交点式,然后代入另一点的坐标,解关于a的一元一次方程
31
知识回顾
知识点三:二次函数解析式的确定
二次函数的解析式
顶点式:y=a(x -h)2+k (a≠0)
交点式:y=a(x - x1)(x- x2)(a≠0)
一般式:y= ax +bx+c(a≠0).
需知:抛物线上不在同一直线上的三点.
需知:顶点及异于顶点的另一点.
需知:与x轴的交点及异于交点的另一端
32
1.若二次函数 y=ax +bx+c,则由表格中的信息可知y与x之间的函数解析式是( )
A.y=x2-4x+3 B. y=x -3x+4 C.y=x - 3x+ 3 D.y=x -4x +8
x -1 0 1
ax 1
ax +bx+c 8 3
知识点三:二次函数解析式的确定
巩固练习
33
知识点三:二次函数解析式的确定
2.二次函数 y=x2 +bx+c 的图象经过点(4,3),(3,0).
(1)求b、c的值;
(2)求该二次函数图象的顶点坐标和对称轴.
巩固练习
34
巩固练习
知识点三:二次函数解析式的确定
3.若二次函数y= ax2 +bx+c的顶点是A(2,1),且经过点B(1,0),求这个二次函数的解析式.
解:根据题意设二次函数解析式为y=a(x -2)2+1.
把点B(1,0)代入得:a(1﹣2)2+1=0
解得:a=﹣1
∴二次函数的解析式是y=﹣(x -2)2+1.
35
知识点三:二次函数解析式的确定
巩固练习
4.二次函数 y=x +px+q的最小值是4,且当 x=2时,y=5,则p,q的值为( ).
A.p=-2,q=15 B.p=-2,q=5或 p=-6,q=13
C.p=-6,q=13 D.p=2,q=-5或 p=6,q=-13
5.若二次函数的图象的顶点坐标为(2,﹣1),且抛物线过(0,3),则二次函数的解析式是( ).
A.y=-(x-2) -1 B.y=- (x-2) - 1 C.y=(x-2)2-1 D.y= (x-2) -1
1
2
1
2
36
知识点三:二次函数解析式的确定
巩固练习
6.已知二次函数 y=x +bx+c 的图像经过点(-1,0),(4,0),
则c= .
7.已知抛物线过点A(2,0),B(-1,0),与y轴交于点C,且OC=2,则这条抛物线的解析式为( ).
A.y=x -x-2 B.y= -x +x+2
C.y=x -x-2或 y=-x +x+2 D.y= -x -x-2或 y= x +x+2
-4
C
37
知识回顾
知识点四:二次函数与一元二次方程
二次函数 y=ax2 +bx+c,当 y=0时,得到一元二次方程 ax2 +bx+c=0,
所以抛物线 y=ax2 +bx+c与x轴的公共点的横坐标就是一元二次方程 ax2 +bx+c=0的根.
38
知识回顾
知识点四:二次函数与一元二次方程
一般地,从二次函数 y=ax2+bx+c 的图象可知:
(2)二次函数的图象与x轴的位置关系有三种:
没有公共点,有一个公共点,有两个公共点;
这对应着一元二次方程根的三种情况:
没有实数根,有两个相等的实数根,有两个不等的实数根
(1)如果抛物线y=ax2+bx+c 与x轴有公共点,公共点的横坐标是x0,那么当x =x0时,函数的值是0,因此x = x0 就是方程 ax2+bx+c=0 的一个根.
39
巩固练习
知识点四:二次函数与一元二次方程
1.二次函数 y=x2- 2x- 3 的图象与 x 轴的两个交点之间的距离为 .
2.若一元二次方程 ax2+bx+c=0 的两根为x1= -3,x2=1,则二次函数 y= ax2+bx+c 的图象的对称轴是直线 .
3.将拋物线 y=x2-1向下平移8个单位长度后与x轴的两个交点之间的距离为( )
A.4 B.6 C.8 D.10
4
x= -1
B
40
巩固练习
知识点四:二次函数与一元二次方程
4.已知抛物线 y=kx +2(k+1)x+k+1 开口向下,且与x轴有两个交点,则k的取值范围是( ).
A.-1
5.已知二次函数 y= -x2+2x+m的部分
图象如图,则关于x的一元二次方程
-x2 +2x+m=0的解为 .
A
x1=3,x2= -1
当已知抛物线与x轴的一个交点的横坐标和对称轴时,可根据轴对称的性质求出抛物线与x轴另一个交点的横坐标,从而求得对应一元二次方程的根.
41
巩固练习
知识点四:二次函数与一元二次方程
6.已知拋物线 y=x2-2x -1与x轴的一个交点为(m ,0).则代数式m2-2m +2018的值为( )
A.2015 B.2016 C.2017 D.2018
7.若关于x的一元二次方程 a(x+m)2 -3=0的两个实数根分别为x1= -1,x2=3,则抛物线 y=a(x+m)2-3与x轴的交点坐标
为 .
D
(3,0),( -1,0)
42
知识回顾
知识点五:二次函数的应用
二次函数解决图形面积问题
求有关几何图形面积的最值问题,往往可转化成求二次函数的最值问题,需要借助几何图形,建立变量之间的二次函数关系,配方将函数解析式转化为顶点式,然后利用二次函数的最值解决问题,要特别注意自变量的取值范围.
43
1.如图,有长为24 m的篱笆,一面利用墙
(墙的最大可用长度为9 m)围成中间隔有一
道篱笆的长方形养鸡场.设养鸡场的长BC为 xm,面积为 ym2.
(1)求 y与x的函数关系,并写出 x 的取值范围.
(2)当长方形的长、宽各为多少时,养鸡场的面积最大,最大的面积是多少
9
墙
B
A
C
D
巩固练习
知识点五:二次函数的应用
二次函数解决图形面积问题
44
2、如图,某小区准备用80m长的篱笆围成一块矩形花圃ABCD,为了节省篱笆,一边利用足够长的墙,另外三边用篱笆围着,再用两段篱笆EF与GH将矩形ABCD分割成①②③三块矩形区域,而且这三块矩形区域的面积相等,设BC的
长度为x m,矩形区域ABCD的面积为y m2.
(1)求y与x 之间的函数关系式,并注明
自变量x 的取值范围;
(2)求x 为何值时,y有最大值 最大值是多少
墙
A
B
C
D
E
F
G
H
区域①
区域②
区域③
巩固练习
知识点五:二次函数的应用
二次函数解决图形面积问题
45
知识回顾
知识点五:二次函数的应用
二次函数求商品的最大利润
在市场销售的利润问题中的等量关系:
总利润=销售总收入﹣总成本;
销售总收入=销售单价×销售量;
总成本=销售量×成本单价.
总利润=单利润×销售量;
46
巩固练习
知识点五:二次函数的应用
二次函数求商品的最大利润
1.某商品的销售利润 W(元)与销售单价x(元)满足函数关系式W= -x2+10x-16,则获得的利润( )
A.最大值为9元 B.最小值为31元
C.最大值为31元 D.最小值为9元
2.已知某商店所销售的毛绒玩具每件的进价为30元,在某段时间内若以每件x元(30≤ x ≤50,且 x 为整数)出售,可卖出(50-x)件,若要使该商店销售该玩具的利润最大,每件的售价为( ).
A
A.35元 B.40元 C.45元 D.48元
B
47
巩固练习
知识点五:二次函数的应用
二次函数求商品的最大利润
3.【2018年安徽省12分】小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元,调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1,W2(单位:元)
(1)用含x的代数式分别表示W1,W2;
(2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少
48
知识回顾
知识点五:二次函数的应用
拱桥类抛物线问题
利用二次函数解决抛物线形的建筑物问题的方法
需要先建立合适的坐标系,一般选择顶点作为原点或选择对称轴作为y轴,然后确定某些点的坐标,再用待定系数法求出函数解析式,最后利用二次函数的图象和性质解题.
49
巩固练习
知识点五:二次函数的应用
拱桥类抛物线问题
1.如图所示,某河面上有一座抛物线形拱桥,
桥下水面在正常水位 AB时,宽为20m,若水
位上升3m,水面就会达到警戒线CD,这时水面宽度为10m.
(1)建立适当的平面直角坐标系并求出抛物线的解析式;
解: (1)以抛物线的顶点为原点,抛物线的对称轴为y轴,建立如图所示的平面直角坐标系.
25a=m,
100a=m-3,
设所求抛物线的解析式为 y=ax2,点D的坐标为D(5,m),则B(10,m-3).
由抛物线经过点D和点B,可得:
a= - ,
m= -1,
∴
20m
10m
x
y
0
∟
∟
50
巩固练习
知识点五:二次函数的应用
拱桥类抛物线问题
1.(2)若洪水到来时,水位以每小时0.2 m的
速度上升从警戒线开始,再持续多少小时就
能到达拱桥的拱顶
20m
10m
20m
10m
x
y
0
∟
∟
51
知识点五:二次函数的应用
2.如图是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景灯.若把拱桥的截面图放
在平面直角坐标系中,则两盏景灯之
间的水平距离是( )m.
A.3 B.4 C.5 D.6
C
巩固练习
拱桥类抛物线问题
52
知识点五:二次函数的应用
巩固练习
抛物线型问题
3.
53
M
y
x
0
A
B
C
N
a
h
其中 a= xC ﹣xB
h= yA ﹣yN
∴S ABC= ah
1
2
知识回顾
抛物线中的三角形的面积
知识点五:二次函数的应用
54
知识回顾
抛物线中的三角形的面积
知识点五:二次函数的应用
利用二次函数的图象和性质解决动态问题的方法
求解动态问题时,常要以“静”制“动”,找出图形在变化过程中不变的量或遵循的数量关系,从而构建函数关系式求解.若在运动过程中,随着自变量的改变,函数关系或图形也发生改变,则需要针对函数关系或图形变化的情况分类讨论.
求解动态问题时,依据图形分析变量间的关系是解题的关键.
55
巩固练习
1.如图,抛物线 y= - x2+3与x轴交于A,B两点,与直线 y= - x+b
相交于B,C两点,连接A,C两点.
(1)写出直线BC的解析式.
(2)求 ABC的面积 .
O
y
x
B
C
A
抛物线中的三角形的面积
知识点五:二次函数的应用
56
巩固练习
抛物线中的三角形的面积
知识点五:二次函数的应用
2.【2016年安徽省12分】如图,二次函数
y=ax +bx的图象经过点A(2,4)与B(6,0).
(1)求a、b的值;
(2)点C是该二次函数图象上A,B两点
之间的一动点,横坐标为 x (2<x<6).写出四边形OACB的面积S关于点C的横坐标 x 的函数表达式,并求S的最大值.
1
2
1
3
-1
y
x
0
4
5
6
7
2
3
4
5
A
B
C
M
57
巩固练习
抛物线中的三角形的面积
知识点五:二次函数的应用
3.如图(1)抛物线 y= -x2+bx+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于C点,点P是抛物线上在要一象限内的一个动点,且点P的横坐标为t
(1)求抛物线的解析式;
P
y
x
0
A
B
C
-1
3
58
巩固练习
抛物线中的三角形的面积
知识点五:二次函数的应用
(2)如图(2),连接BC,PB.PC.设 PBC的面积为S.
①求S关于t的函数解析式;
②求P点到直线BC的距离的最大值。并求出此时点P的坐标.
P
y
x
0
A
B
C
M
-1
3
3
知识结构图
59
60
对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?
蓦然回首
同课章节目录
