三角形的概念和全等三角形[下学期]
文档属性
| 名称 | 三角形的概念和全等三角形[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 170.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-04-13 07:19:00 | ||
图片预览



文档简介
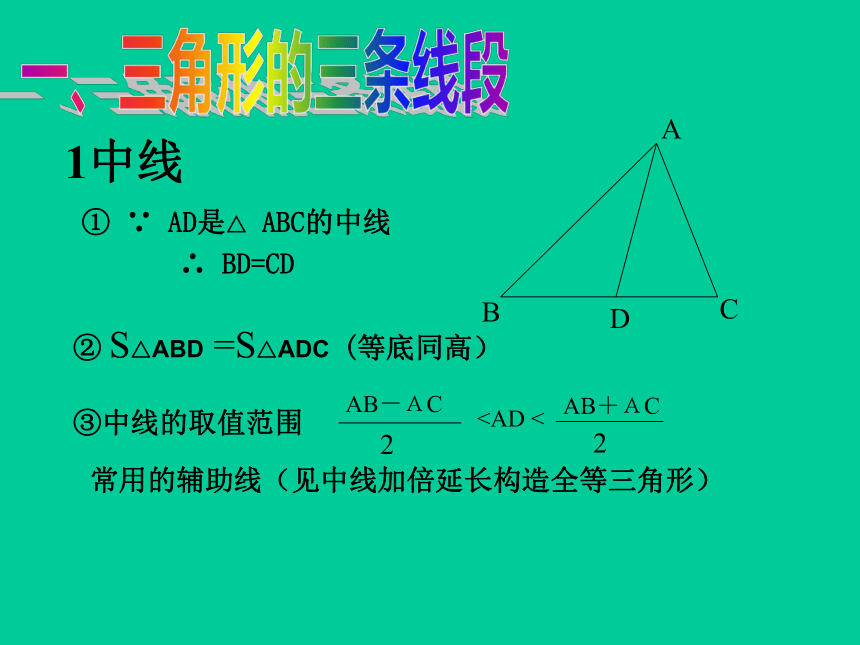
课件17张PPT。三角形的概念和全等三角形山亭育才中学 翟夫连① ∵ AD是△ ABC的中线
∴ BD=CD
② S△ABD =S△ADC (等底同高) ③中线的取值范围
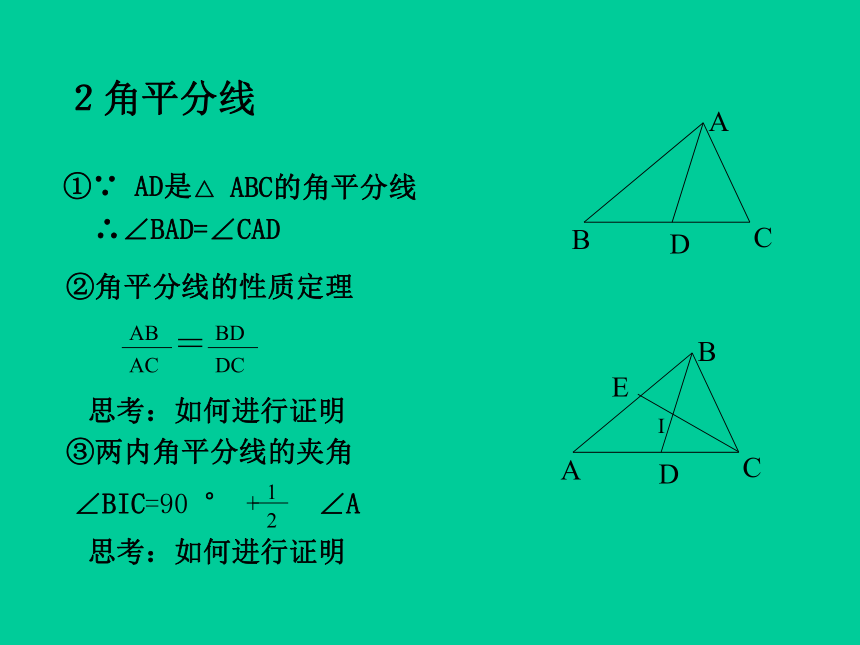
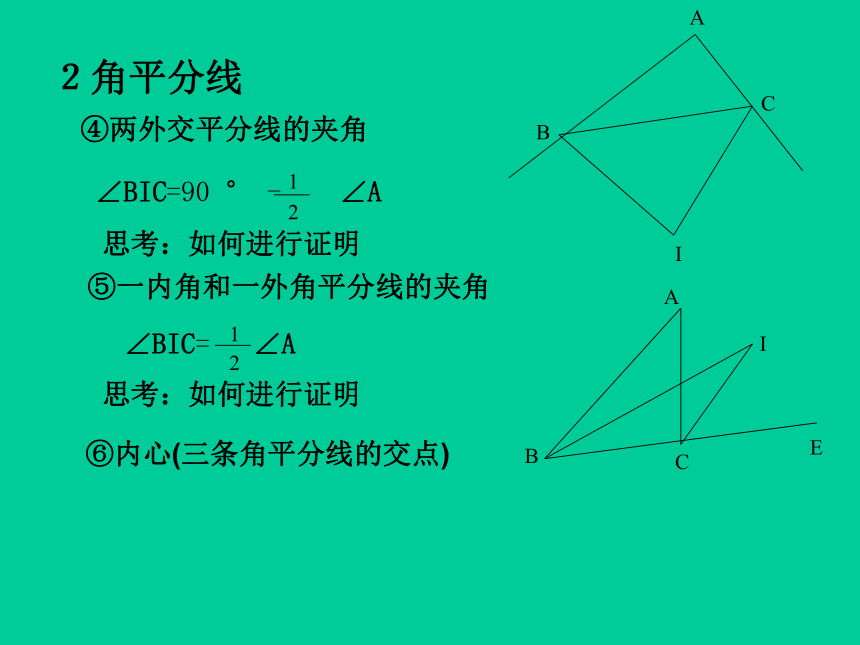
常用的辅助线(见中线加倍延长构造全等三角形)1中线一、三角形的三条线段1中线④重心(三条中线的交点)EG⑤比例2角平分线②角平分线的性质定理思考:如何进行证明思考:如何进行证明③两内角平分线的夹角2角平分线④两外交平分线的夹角思考:如何进行证明⑤一内角和一外角平分线的夹角思考:如何进行证明⑥内心(三条角平分线的交点)3高线① ∵ AD是△ ABC的高线
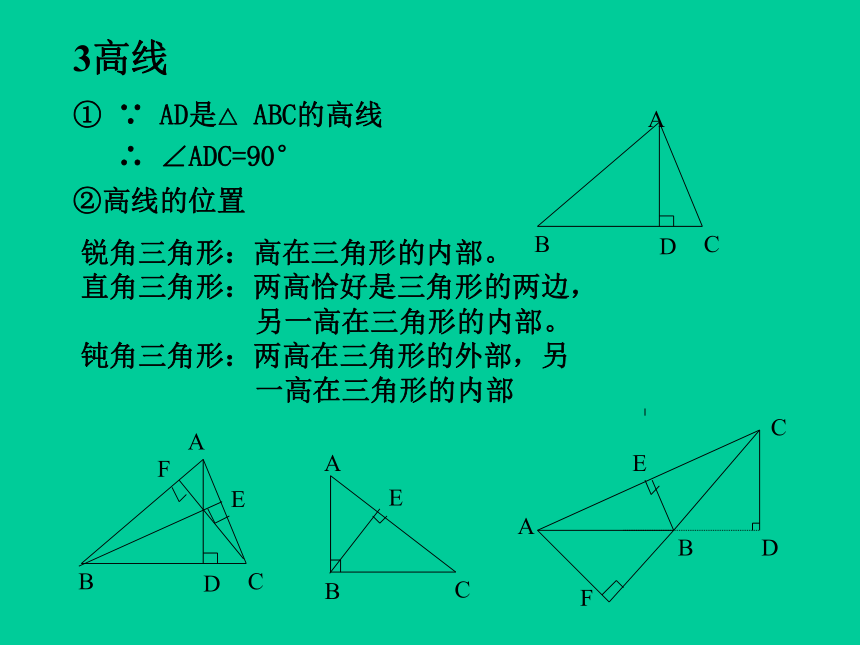
∴ ∠ADC=90°②高线的位置锐角三角形:高在三角形的内部。
直角三角形:两高恰好是三角形的两边,
另一高在三角形的内部。
钝角三角形:两高在三角形的外部,另
一高在三角形的内部④两高线的夹角例: 在斜三角形中∠A=45° ,
BD垂直于AC于D,CE垂直于AB
于ED点,求BD、CE之间的夹角
反思:为什么会出现漏解现象?⑤一高线和一角平分线的夹角。例 :已知△ABC中,AB>AC,AD垂直
于BC于D,AE是角平分线⑥垂心(三条高的交点)③面积相等。写出关系式3高线例1 如图:△ABC中,∠A=90°AB=AC=BE,E是BC上一点,DE⊥BC,如果BC=10cm,那么△DEC的周长是_______cm例2 如图,在△ABC中,点O是内心, (1)若∠ABC=50°∠ACB=70°,求∠BOC的度数解(1)∵点O是△ABC的内心,
∴ ∠OBC= ∠OBA= ∠ABC= 25 °
同理 ∠OCB= ∠OCA= ∠ACB=35 °
∴ ∠BOC=180 °- (∠OBC+ ∠OCB) = 180 °-60 °=120 ° (2)若∠A=80 °,则∠BOC= 度。
(3)若∠BOC=100 °,则∠A= 度。
13020(4)试探索: ∠A与∠BOC之间存在怎样
的数量关系?请说明理由。
答: ∠BOC =90 ° + ∠A
理由: ∵点O是△ABC的内心,
∴ ∠OBC= ∠ABC, ∠OCB= ∠ACB
∴ ∠OBC+ ∠OCB = (∠ABC+ ∠ACB)
= (180 ° - ∠A )= 90 ° - ∠A
在△ABC中, ∠BOC =180 °-( ∠OBC+ ∠OCB )
= 180 °-( 90 ° - ∠A )= 90 °+ ∠A
二、三角形的分类1、三角形按边的关系分类可以分为不等边三角形等腰三角形等边三角形底与腰不等的等腰三角形2、三角形按角的大小关系分类可以分为钝角三角形锐角三角形斜三角形直角三角形三、三角形的边角关系两边之和大于第三边两边之差小于第三边三角形内角和等于180 0三角形的一个外角等于不相邻的两内角和三角形的一个外角大于任一个不相邻的内角12四、全等三角形的判定两个三角形
全等的条件①两边一角:SAS (夹角)②两角一边ASA (夹边)AAS (对边)③三边 SSS④斜边、直角边”或“HL”判断题:1.全等图形是指面积大小一样的图形2.两个等边三角形一定是全等图形 3.周长相等的两个正方形面积也相等 4.全等三角形的对应高不一定相等5、全等三角形的周长相等,面积相等 6、面积相等的两个三角形全等。( )×如图所示,已知M是正方形ABCD的边AB的中点,MN⊥MD交∠CBE的平分线BN于点N,求证:MD=MN例31如图①所示,△ABC中,∠BAC=90°,AB=AC,AE是过
A点的一条直线,且B点和C点在AE的异侧,BD⊥AE于
D点, CE⊥AE于E点;2如图②求证:若直线AE绕A旋转到图②所示位置时(BD其余条件不变,问BD与DE、CE关系如何?请证明。3如图③求证:若直线AE绕点A旋转到图③所示位置时
(BD>CE),其余条件不变,问BD与DE、CE关系如何?直
接写出结论,不必证明。 ④归纳前面三题,用语言表达BD与DE、CE的关系。例4①②③忠心祝福我们每个同学都可以给
这一章画上一个完美的句号!
∴ BD=CD
② S△ABD =S△ADC (等底同高) ③中线的取值范围
常用的辅助线(见中线加倍延长构造全等三角形)1中线一、三角形的三条线段1中线④重心(三条中线的交点)EG⑤比例2角平分线②角平分线的性质定理思考:如何进行证明思考:如何进行证明③两内角平分线的夹角2角平分线④两外交平分线的夹角思考:如何进行证明⑤一内角和一外角平分线的夹角思考:如何进行证明⑥内心(三条角平分线的交点)3高线① ∵ AD是△ ABC的高线
∴ ∠ADC=90°②高线的位置锐角三角形:高在三角形的内部。
直角三角形:两高恰好是三角形的两边,
另一高在三角形的内部。
钝角三角形:两高在三角形的外部,另
一高在三角形的内部④两高线的夹角例: 在斜三角形中∠A=45° ,
BD垂直于AC于D,CE垂直于AB
于ED点,求BD、CE之间的夹角
反思:为什么会出现漏解现象?⑤一高线和一角平分线的夹角。例 :已知△ABC中,AB>AC,AD垂直
于BC于D,AE是角平分线⑥垂心(三条高的交点)③面积相等。写出关系式3高线例1 如图:△ABC中,∠A=90°AB=AC=BE,E是BC上一点,DE⊥BC,如果BC=10cm,那么△DEC的周长是_______cm例2 如图,在△ABC中,点O是内心, (1)若∠ABC=50°∠ACB=70°,求∠BOC的度数解(1)∵点O是△ABC的内心,
∴ ∠OBC= ∠OBA= ∠ABC= 25 °
同理 ∠OCB= ∠OCA= ∠ACB=35 °
∴ ∠BOC=180 °- (∠OBC+ ∠OCB) = 180 °-60 °=120 ° (2)若∠A=80 °,则∠BOC= 度。
(3)若∠BOC=100 °,则∠A= 度。
13020(4)试探索: ∠A与∠BOC之间存在怎样
的数量关系?请说明理由。
答: ∠BOC =90 ° + ∠A
理由: ∵点O是△ABC的内心,
∴ ∠OBC= ∠ABC, ∠OCB= ∠ACB
∴ ∠OBC+ ∠OCB = (∠ABC+ ∠ACB)
= (180 ° - ∠A )= 90 ° - ∠A
在△ABC中, ∠BOC =180 °-( ∠OBC+ ∠OCB )
= 180 °-( 90 ° - ∠A )= 90 °+ ∠A
二、三角形的分类1、三角形按边的关系分类可以分为不等边三角形等腰三角形等边三角形底与腰不等的等腰三角形2、三角形按角的大小关系分类可以分为钝角三角形锐角三角形斜三角形直角三角形三、三角形的边角关系两边之和大于第三边两边之差小于第三边三角形内角和等于180 0三角形的一个外角等于不相邻的两内角和三角形的一个外角大于任一个不相邻的内角12四、全等三角形的判定两个三角形
全等的条件①两边一角:SAS (夹角)②两角一边ASA (夹边)AAS (对边)③三边 SSS④斜边、直角边”或“HL”判断题:1.全等图形是指面积大小一样的图形2.两个等边三角形一定是全等图形 3.周长相等的两个正方形面积也相等 4.全等三角形的对应高不一定相等5、全等三角形的周长相等,面积相等 6、面积相等的两个三角形全等。( )×如图所示,已知M是正方形ABCD的边AB的中点,MN⊥MD交∠CBE的平分线BN于点N,求证:MD=MN例31如图①所示,△ABC中,∠BAC=90°,AB=AC,AE是过
A点的一条直线,且B点和C点在AE的异侧,BD⊥AE于
D点, CE⊥AE于E点;2如图②求证:若直线AE绕A旋转到图②所示位置时(BD
(BD>CE),其余条件不变,问BD与DE、CE关系如何?直
接写出结论,不必证明。 ④归纳前面三题,用语言表达BD与DE、CE的关系。例4①②③忠心祝福我们每个同学都可以给
这一章画上一个完美的句号!
