2022-2023鲁教版数学九年级上册第二章直角三角形的边角关系单元测试(含答案)
文档属性
| 名称 | 2022-2023鲁教版数学九年级上册第二章直角三角形的边角关系单元测试(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 261.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-19 11:33:34 | ||
图片预览


文档简介
2022-2023鲁教版数学九年级上册第二章直角三角形的边角关系单元测试
一、选择题
的值等于( )
A. B. C. D.
在中,,,,则边的长是( )
A. B. C. D.
如图,在的正方形网格中,每个小正方形的边长都是,的顶点都在这些小正方形的顶点上,那么的值为( )
A.
B.
C.
D.
如图,在中,,,垂足为给出下列四个结论:其中正确的结论有( )
A. 个 B. 个 C. 个 D. 个
在中,若,满足,则是( )
A. 等腰非等边三角形 B. 等边三角形 C. 直角三角形 D. 钝角三角形
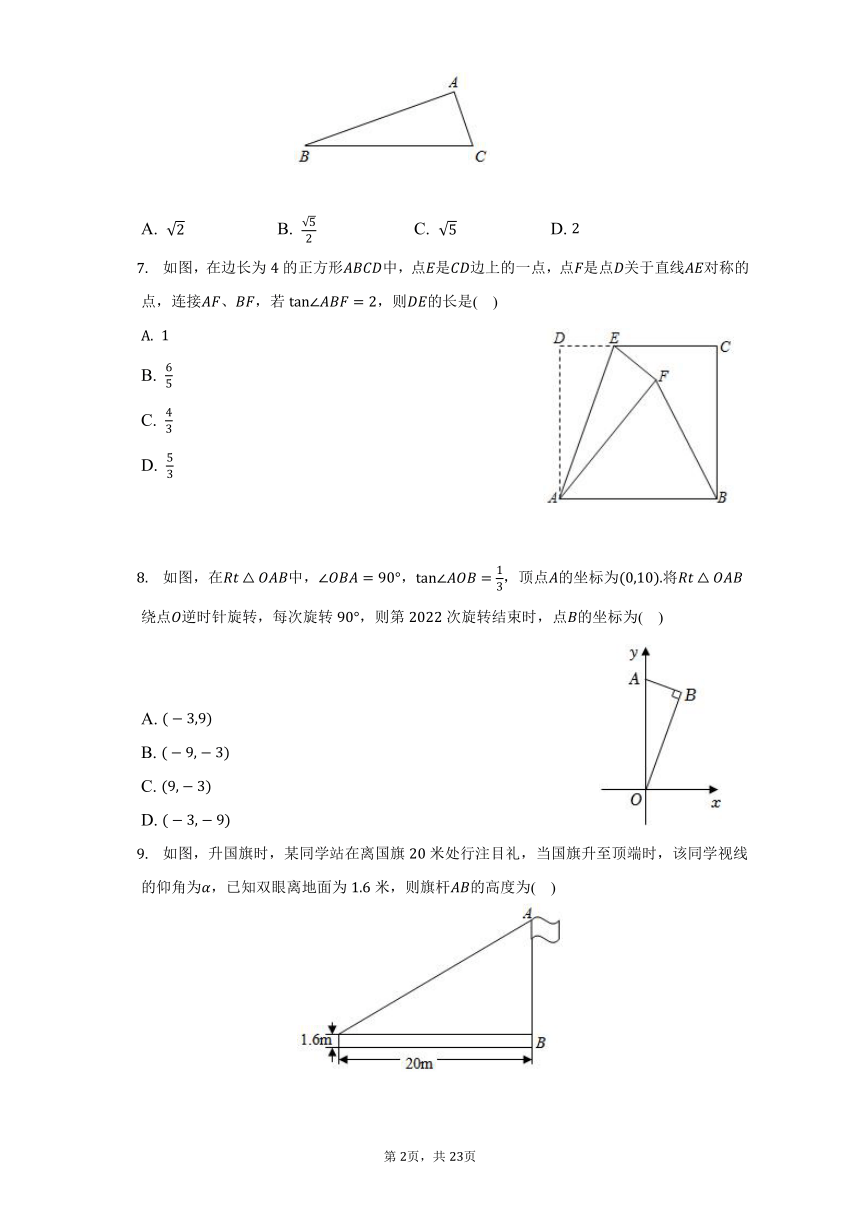
如图,在中,,,,则的长为( )
A. B. C. D.
如图,在边长为的正方形中,点是边上的一点,点是点关于直线对称的点,连接、,若,则的长是( )
B.
C.
D.
如图,在中,,,顶点的坐标为将绕点逆时针旋转,每次旋转,则第次旋转结束时,点的坐标为( )
A.
B.
C.
D.
如图,升国旗时,某同学站在离国旗米处行注目礼,当国旗升至顶端时,该同学视线的仰角为,已知双眼离地面为米,则旗杆的高度为( )
A. 米 B. 米
C. 米 D. 米
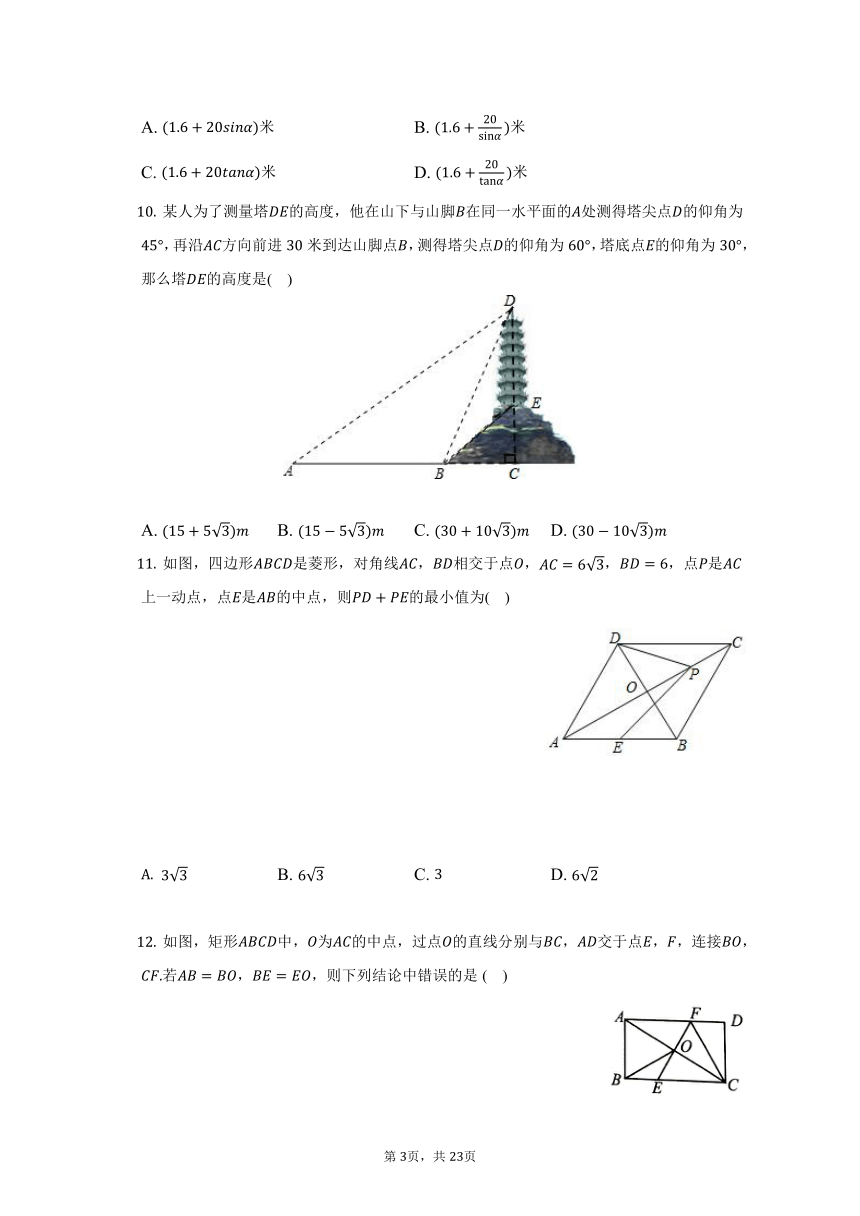
某人为了测量塔的高度,他在山下与山脚在同一水平面的处测得塔尖点的仰角为,再沿方向前进米到达山脚点,测得塔尖点的仰角为,塔底点的仰角为,那么塔的高度是( )
A. B. C. D.
如图,四边形是菱形,对角线,相交于点,,,点是上一动点,点是的中点,则的最小值为( )
B. C. D.
如图,矩形中,为的中点,过点的直线分别与,交于点,,连接,若,,则下列结论中错误的是( )
A. B.
C. D.
二、填空题
在中,、为锐角,且,则____.
如图,在矩形中,边沿折叠,点恰好落在矩形的对称中心处,则______.
如图,在中,,点为边的中点,连接,若,,则的值为______.
如图,已知,,点是射线上一动点,当为直角三角形时,则______.
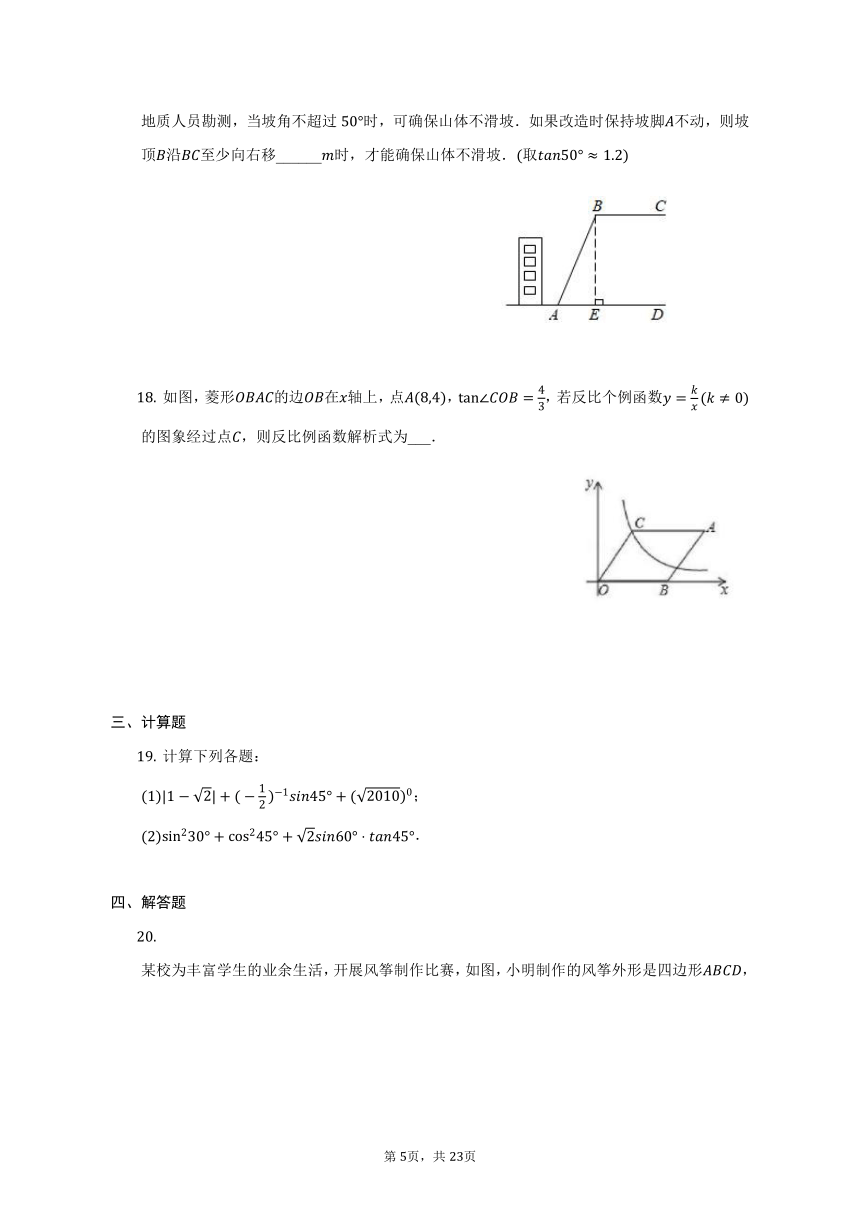
如图,某校教学楼后面紧邻着一个山坡,坡上面是一块平地.,,斜坡长,斜坡的坡比为:为了减缓坡面,防止山体滑坡,学校决定对该斜坡进行改造.经地质人员勘测,当坡角不超过时,可确保山体不滑坡.如果改造时保持坡脚不动,则坡顶沿至少向右移______时,才能确保山体不滑坡.取
如图,菱形的边在轴上,点,,若反比个例函数的图象经过点,则反比例函数解析式为___.
三、计算题
计算下列各题:
;
.
四、解答题
某校为丰富学生的业余生活,开展风筝制作比赛,如图,小明制作的风筝外形是四边形,其中,.
若,求的度数.
若,,,求的长精确到.
如图,在中,,为上一点,,,.
求的长;
求的值.
如图,在中,,点,、分别为,,的中点,连接,.
求证:四边形是矩形;
连接,若,,求的长.
如图,处是一钻井平台,位于东营港口的北偏东方向上,与港口相距海里,一艘摩托艇从出发,自西向东航行至时,改变航向以每小时海里的速度沿方向行进,此时位于的北偏西方向,则从到达需要多少小时?
开封清明上河图是依照北宋著名画家张择端的清明上河图建造的,拂云阁是园内最高的建筑.某数学小组测量拂云阁的高度,如图,在处用测角仪测得拂云阁顶端的仰角为,沿方向前进到达处,又测得拂云阁顶端的仰角为已知测角仪的高度为,测量点,与拂云阁的底部在同一水平线上,求拂云阁的高度结果精确到参考数据:,,.
1.【答案】
【解析】
【分析】
本题考查的是特殊角度的三角函数值,熟记特殊角度的三角函数值是解答此题的关键.根据各特殊角的三角函数值解答即可.
【解答】
解:由特殊角的三角函数值可知: .
故选D.
2.【答案】
【解析】解:,,
.
故选A.
先根据,求出的长度,再利用勾股定理即可求解.
本题利用角的正弦的定义和勾股定理.
3.【答案】
【解析】
【分析】
本题考查锐角三角函数的定义,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.
如图,过点作于利用勾股定理求出即可解决问题.
【解答】
解:如图,过点作于.
在中,,,
,
,
故选:.
4.【答案】
【解析】略
5.【答案】
【解析】
【试题解析】
【分析】
本题考查了特殊角的三角函数值、非负数的性质:绝对值、非负数的性质:偶次方.
根据非负数的性质得到,,再根据特殊角的三角函数值得到,,然后根据等边三角形的判定方法进行判断.
【解答】
解:根据题意得,,
,,
,,
为等边三角形.
故选B.
6.【答案】
【解析】解:过点作交于点,则,
,,
,,
,
,,
在中,由勾股定理,得.
故选:.
本题考查了解直角三角形,勾股定理,锐角三角函数的定义等知识点,能熟记锐角三角函数的定义是解此题的关键.
过点作交于点,则,根据已知求出,,求出、的长,根据勾股定理求出即可.
7.【答案】
【解析】解:过点作于点,并延长交于点,
,
,
,
,
,
设,则,
,
点是点关于直线对称的点,
,,
,
≌,
,
,
,
舍,,
,,
,
,
,
,即,
,
.
故选:.
过点作于点,并延长交于点,设,则,则,由对称的性质得出,,证明≌,得,由勾股定理求出,由锐角三角函数的定义可得出答案.
本题考查了正方形的性质,勾股定理,锐角三角函数以及对称的性质,熟练掌握对称的性质是解题的关键.
8.【答案】
【解析】解:如图,过点作轴于点,
点的坐标为,
,
,
设,则,
在中,,
,
解得,
,
在中,设,则,
,
解得,
,则,
,
绕点逆时针旋转,每次旋转,
则第次旋转结束时,点的坐标为;
则第次旋转结束时,点的坐标为;
则第次旋转结束时,点的坐标为;
则第次旋转结束时,点的坐标为;
发现规律:旋转次一个循环,
,
则第次旋转结束时,点的坐标为.
故选:.
先得出,再利用解直角三角形的知识确定,由于,所以第次旋转结束时,相当于绕点逆时针旋转次,由此求出点坐标即可.
本题考查图形的旋转,通过旋转角度找到旋转规律,从而确定第次旋转后直角三角形的位置是解题的关键.
9.【答案】
【解析】解:如图,米,米,
四边形为矩形,则米,米,
在中,
,
,
米.
故选:.
由题意可知,在直角三角形中,已知角和邻边,要求出对边,直接用正切即可解答.
本题考查仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形.
10.【答案】
【解析】解:设米,
在中,,
米,
米,
米,
在中,,
,
,
经检验:是原方程的根,
米,米,
在中,,
米,
米,
故选:.
设米,先在中,利用锐角三角函数的定义求出的长,然后在中,利用锐角三角函数的定义列出关于的方程,进行计算即可求出,的长,再在中,利用锐角三角函数的定义求出的长,进行计算即可解答.
本题考查了解直角三角形的应用仰角俯角问题,熟练掌握锐角三角函数的定义是解题的关键.
11.【答案】
【解析】
【分析】
本题考查了三角形的三边关系,菱形的性质,等边三角形的判定和性质,锐角三角函数等知识,证明是等边三角形是解题的关键.
由三角形的三边关系可得当点在上时,的最小值为的长,由菱形的性质可得,,,,由锐角三角函数可求,可证是等边三角形,由等边三角形的性质可得,即可求解.
【解答】
解:如图,连接,
在中,,
当点在上时,的最小值为的长,
四边形是菱形,
,,,,
,
,
是等边三角形,
点是的中点,
,
,
,
,
故选A.
12.【答案】
【解析】
【分析】
本题考查矩形的性质、菱形的判定和性质、等边三角形的判定和性质,掌握矩形和菱形的性质是解题的关键根据矩形性质和直角三角形性质判断为等边三角形,可求,判断;连接,得到四边形为菱形,判断为等边三角形,判断;根据矩形是以点为对称中心的中心对称图形,可得,判断;根据特殊角三角函数值求得,判断.
【解答】
解:四边形为矩形,为的中点,
,
,
,
为等边三角形,
,
,
,
,
,故A正确;
连接,则四边形为菱形,
,
,
,
又,
为等边三角形,
,故B正确;
根据矩形是以点为对称中心的中心对称图形,
,,
而,
,
,故C正确;
在中,,,
,
,故D错误.
故选D.
13.【答案】
【解析】解:由题意得,,,
因为、为锐角,
所以,,,
则.
故答案为:.
根据非负数的性质求出和的值,然后求出、的度数,最后求出.
本题考查了特殊角的三角函数值,解答本题的关键是掌握几个特殊角的三角函数值.
14.【答案】
【解析】
【分析】
本题考查了折叠的性质,矩形的性质,中心对称,等边三角形的判定和性质及锐角三角函数的定义,熟练掌握矩形的性质是解题的关键.根据折叠的性质得到,,推出的等边三角形,根据等边三角形的性质得到,求得,再根据特殊锐角的三角函数值即可得到结论.
【解答】
解:如图,连接,
把边沿折叠,点恰好落在矩形的对称中心处,
,,
的等边三角形,
,
,
,
故答案为.
15.【答案】
【解析】解:过点作,垂足为,
,,
,
又点为边的中点,
,
在中,,
故答案为:.
过点作,由平行线平分线段定理可得是的中点,再根据三角函数的定义,可求出答案.
本题考查直角三角形的边角关系,理解直角三角形的边角关系是得出正确答案的前提,作高构造直角三角形是常用的方法.
16.【答案】或
【解析】解:当时,,
则,,
;
当时,,
则,
设,则,
由勾股定理得:,
解得:,
;
综上所述,的长为或;
故答案为:或.
分别从若与若去分析求解,根据三角函数和勾股定理,即可求得答案.
此题考查了直角三角形的性质,注意掌握分类讨论思想的应用.
17.【答案】
【解析】解:在上取点,使,过点作于,
,,,
四边形为矩形,
,,
斜坡的坡比为:,
,
设,则,
由勾股定理得,,即,
解得,,
,,
,
在中,,
,
,
坡顶沿至少向右移时,才能确保山体不滑坡,
故答案为:.
在上取点,使,作,根据坡度的概念求出、,根据正切的定义求出,结合图形计算,得到答案.
本题考查的是解直角三角形的应用坡度坡角问题,掌握坡度坡角的概念、熟记锐角三角函数的定义是解题的关键.
18.【答案】
【解析】解:过作垂直于于,
四边形是菱形,,
,
又,
,
点,
点在反比例函数的图象上,
,
反比例函数关系式为,
故答案为:.
根据菱形的性质和点的坐标可求出,再由锐角三角函数可求出,进而确定点的坐标,再将点的坐标代入函数关系式即可.
本题考查菱形的性质,锐角三角函数的定义以及反比例函数图象上点值坐标的特征是解决问题的关键.
19.【答案】解:
;
.
【解析】按先算负整数指数幂、零指数幂、绝对值及三角函数,再算乘法,最后计算加减;
按先算三角函数,再算乘方,后算乘除,最后计算加减的顺序计算即可.
此题考查了实数混合运算的能力,关键是能确定正确的运算顺序,并能进行准确计算.
20.【答案】略
【解析】略
21.【答案】解:,可设,得,
,
,
解得,舍去,或,
,,
,
,
;
过点作于点,
,可设,则,
,
,
解得,舍,或,
,
.
【解析】本题是解直角三角形的应用,主要考查了解直角三角形,勾股定理,第二小题关键是构造直角三角形.
根据,可设,得,再由勾股定理列出的方程求得,进而由勾股定理求;
过点作于点,解直角三角形求得与,进而求得结果.
22.【答案】证明:点,、分别为,,的中点,
,,
四边形是平行四边形,
,
四边形是矩形;
解:,,,
,
即,
解得,
点为的中点,
,
,
即的长是.
【解析】根据三角形的中位线和矩形的判定方法可以证明结论成立;
根据,,可以得到的长,然后即可得到的长,再根据勾股定理,
即可求得的长.
本题考查矩形的判定、勾股定理、解直角三角形,解答本题的关键是明确矩形的判定方法,
利用数形结合的思想解答.
23.【答案】解:过作于,在点的正北方向上取点,在点的正北方向上取点,
由题意得:,,,海里,
,
在中,,
海里,
在中,,,
海里,
小时,
从处到达处需要小时.
【解析】此题考查了解直角三角形的应用方向角,熟练掌握锐角三角函数定义是解本题的关键.过作于,在点的正北方向上取点,在点的正北方向上取点,在直角三角形中,求出的长,在直角三角形中,利用锐角三角函数定义求出的长,进而求出所求时间即可.
24.【答案】解:延长交于点,
由题意得:
,米,米,
设米,
米,
在中,,
米,
在中,,
,
,
经检验:是原方程的根,
米,
拂云阁的高度约为米.
【解析】延长交于点,根据题意可得:,米,米,设米,在中,利用锐角三角函数的定义求出的长,然后在中,利用锐角三角函数的定义列出关于的方程,进行计算即可解答.
本题考查了解直角三角形的应用仰角俯角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
第1页,共1页
一、选择题
的值等于( )
A. B. C. D.
在中,,,,则边的长是( )
A. B. C. D.
如图,在的正方形网格中,每个小正方形的边长都是,的顶点都在这些小正方形的顶点上,那么的值为( )
A.
B.
C.
D.
如图,在中,,,垂足为给出下列四个结论:其中正确的结论有( )
A. 个 B. 个 C. 个 D. 个
在中,若,满足,则是( )
A. 等腰非等边三角形 B. 等边三角形 C. 直角三角形 D. 钝角三角形
如图,在中,,,,则的长为( )
A. B. C. D.
如图,在边长为的正方形中,点是边上的一点,点是点关于直线对称的点,连接、,若,则的长是( )
B.
C.
D.
如图,在中,,,顶点的坐标为将绕点逆时针旋转,每次旋转,则第次旋转结束时,点的坐标为( )
A.
B.
C.
D.
如图,升国旗时,某同学站在离国旗米处行注目礼,当国旗升至顶端时,该同学视线的仰角为,已知双眼离地面为米,则旗杆的高度为( )
A. 米 B. 米
C. 米 D. 米
某人为了测量塔的高度,他在山下与山脚在同一水平面的处测得塔尖点的仰角为,再沿方向前进米到达山脚点,测得塔尖点的仰角为,塔底点的仰角为,那么塔的高度是( )
A. B. C. D.
如图,四边形是菱形,对角线,相交于点,,,点是上一动点,点是的中点,则的最小值为( )
B. C. D.
如图,矩形中,为的中点,过点的直线分别与,交于点,,连接,若,,则下列结论中错误的是( )
A. B.
C. D.
二、填空题
在中,、为锐角,且,则____.
如图,在矩形中,边沿折叠,点恰好落在矩形的对称中心处,则______.
如图,在中,,点为边的中点,连接,若,,则的值为______.
如图,已知,,点是射线上一动点,当为直角三角形时,则______.
如图,某校教学楼后面紧邻着一个山坡,坡上面是一块平地.,,斜坡长,斜坡的坡比为:为了减缓坡面,防止山体滑坡,学校决定对该斜坡进行改造.经地质人员勘测,当坡角不超过时,可确保山体不滑坡.如果改造时保持坡脚不动,则坡顶沿至少向右移______时,才能确保山体不滑坡.取
如图,菱形的边在轴上,点,,若反比个例函数的图象经过点,则反比例函数解析式为___.
三、计算题
计算下列各题:
;
.
四、解答题
某校为丰富学生的业余生活,开展风筝制作比赛,如图,小明制作的风筝外形是四边形,其中,.
若,求的度数.
若,,,求的长精确到.
如图,在中,,为上一点,,,.
求的长;
求的值.
如图,在中,,点,、分别为,,的中点,连接,.
求证:四边形是矩形;
连接,若,,求的长.
如图,处是一钻井平台,位于东营港口的北偏东方向上,与港口相距海里,一艘摩托艇从出发,自西向东航行至时,改变航向以每小时海里的速度沿方向行进,此时位于的北偏西方向,则从到达需要多少小时?
开封清明上河图是依照北宋著名画家张择端的清明上河图建造的,拂云阁是园内最高的建筑.某数学小组测量拂云阁的高度,如图,在处用测角仪测得拂云阁顶端的仰角为,沿方向前进到达处,又测得拂云阁顶端的仰角为已知测角仪的高度为,测量点,与拂云阁的底部在同一水平线上,求拂云阁的高度结果精确到参考数据:,,.
1.【答案】
【解析】
【分析】
本题考查的是特殊角度的三角函数值,熟记特殊角度的三角函数值是解答此题的关键.根据各特殊角的三角函数值解答即可.
【解答】
解:由特殊角的三角函数值可知: .
故选D.
2.【答案】
【解析】解:,,
.
故选A.
先根据,求出的长度,再利用勾股定理即可求解.
本题利用角的正弦的定义和勾股定理.
3.【答案】
【解析】
【分析】
本题考查锐角三角函数的定义,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.
如图,过点作于利用勾股定理求出即可解决问题.
【解答】
解:如图,过点作于.
在中,,,
,
,
故选:.
4.【答案】
【解析】略
5.【答案】
【解析】
【试题解析】
【分析】
本题考查了特殊角的三角函数值、非负数的性质:绝对值、非负数的性质:偶次方.
根据非负数的性质得到,,再根据特殊角的三角函数值得到,,然后根据等边三角形的判定方法进行判断.
【解答】
解:根据题意得,,
,,
,,
为等边三角形.
故选B.
6.【答案】
【解析】解:过点作交于点,则,
,,
,,
,
,,
在中,由勾股定理,得.
故选:.
本题考查了解直角三角形,勾股定理,锐角三角函数的定义等知识点,能熟记锐角三角函数的定义是解此题的关键.
过点作交于点,则,根据已知求出,,求出、的长,根据勾股定理求出即可.
7.【答案】
【解析】解:过点作于点,并延长交于点,
,
,
,
,
,
设,则,
,
点是点关于直线对称的点,
,,
,
≌,
,
,
,
舍,,
,,
,
,
,
,即,
,
.
故选:.
过点作于点,并延长交于点,设,则,则,由对称的性质得出,,证明≌,得,由勾股定理求出,由锐角三角函数的定义可得出答案.
本题考查了正方形的性质,勾股定理,锐角三角函数以及对称的性质,熟练掌握对称的性质是解题的关键.
8.【答案】
【解析】解:如图,过点作轴于点,
点的坐标为,
,
,
设,则,
在中,,
,
解得,
,
在中,设,则,
,
解得,
,则,
,
绕点逆时针旋转,每次旋转,
则第次旋转结束时,点的坐标为;
则第次旋转结束时,点的坐标为;
则第次旋转结束时,点的坐标为;
则第次旋转结束时,点的坐标为;
发现规律:旋转次一个循环,
,
则第次旋转结束时,点的坐标为.
故选:.
先得出,再利用解直角三角形的知识确定,由于,所以第次旋转结束时,相当于绕点逆时针旋转次,由此求出点坐标即可.
本题考查图形的旋转,通过旋转角度找到旋转规律,从而确定第次旋转后直角三角形的位置是解题的关键.
9.【答案】
【解析】解:如图,米,米,
四边形为矩形,则米,米,
在中,
,
,
米.
故选:.
由题意可知,在直角三角形中,已知角和邻边,要求出对边,直接用正切即可解答.
本题考查仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形.
10.【答案】
【解析】解:设米,
在中,,
米,
米,
米,
在中,,
,
,
经检验:是原方程的根,
米,米,
在中,,
米,
米,
故选:.
设米,先在中,利用锐角三角函数的定义求出的长,然后在中,利用锐角三角函数的定义列出关于的方程,进行计算即可求出,的长,再在中,利用锐角三角函数的定义求出的长,进行计算即可解答.
本题考查了解直角三角形的应用仰角俯角问题,熟练掌握锐角三角函数的定义是解题的关键.
11.【答案】
【解析】
【分析】
本题考查了三角形的三边关系,菱形的性质,等边三角形的判定和性质,锐角三角函数等知识,证明是等边三角形是解题的关键.
由三角形的三边关系可得当点在上时,的最小值为的长,由菱形的性质可得,,,,由锐角三角函数可求,可证是等边三角形,由等边三角形的性质可得,即可求解.
【解答】
解:如图,连接,
在中,,
当点在上时,的最小值为的长,
四边形是菱形,
,,,,
,
,
是等边三角形,
点是的中点,
,
,
,
,
故选A.
12.【答案】
【解析】
【分析】
本题考查矩形的性质、菱形的判定和性质、等边三角形的判定和性质,掌握矩形和菱形的性质是解题的关键根据矩形性质和直角三角形性质判断为等边三角形,可求,判断;连接,得到四边形为菱形,判断为等边三角形,判断;根据矩形是以点为对称中心的中心对称图形,可得,判断;根据特殊角三角函数值求得,判断.
【解答】
解:四边形为矩形,为的中点,
,
,
,
为等边三角形,
,
,
,
,
,故A正确;
连接,则四边形为菱形,
,
,
,
又,
为等边三角形,
,故B正确;
根据矩形是以点为对称中心的中心对称图形,
,,
而,
,
,故C正确;
在中,,,
,
,故D错误.
故选D.
13.【答案】
【解析】解:由题意得,,,
因为、为锐角,
所以,,,
则.
故答案为:.
根据非负数的性质求出和的值,然后求出、的度数,最后求出.
本题考查了特殊角的三角函数值,解答本题的关键是掌握几个特殊角的三角函数值.
14.【答案】
【解析】
【分析】
本题考查了折叠的性质,矩形的性质,中心对称,等边三角形的判定和性质及锐角三角函数的定义,熟练掌握矩形的性质是解题的关键.根据折叠的性质得到,,推出的等边三角形,根据等边三角形的性质得到,求得,再根据特殊锐角的三角函数值即可得到结论.
【解答】
解:如图,连接,
把边沿折叠,点恰好落在矩形的对称中心处,
,,
的等边三角形,
,
,
,
故答案为.
15.【答案】
【解析】解:过点作,垂足为,
,,
,
又点为边的中点,
,
在中,,
故答案为:.
过点作,由平行线平分线段定理可得是的中点,再根据三角函数的定义,可求出答案.
本题考查直角三角形的边角关系,理解直角三角形的边角关系是得出正确答案的前提,作高构造直角三角形是常用的方法.
16.【答案】或
【解析】解:当时,,
则,,
;
当时,,
则,
设,则,
由勾股定理得:,
解得:,
;
综上所述,的长为或;
故答案为:或.
分别从若与若去分析求解,根据三角函数和勾股定理,即可求得答案.
此题考查了直角三角形的性质,注意掌握分类讨论思想的应用.
17.【答案】
【解析】解:在上取点,使,过点作于,
,,,
四边形为矩形,
,,
斜坡的坡比为:,
,
设,则,
由勾股定理得,,即,
解得,,
,,
,
在中,,
,
,
坡顶沿至少向右移时,才能确保山体不滑坡,
故答案为:.
在上取点,使,作,根据坡度的概念求出、,根据正切的定义求出,结合图形计算,得到答案.
本题考查的是解直角三角形的应用坡度坡角问题,掌握坡度坡角的概念、熟记锐角三角函数的定义是解题的关键.
18.【答案】
【解析】解:过作垂直于于,
四边形是菱形,,
,
又,
,
点,
点在反比例函数的图象上,
,
反比例函数关系式为,
故答案为:.
根据菱形的性质和点的坐标可求出,再由锐角三角函数可求出,进而确定点的坐标,再将点的坐标代入函数关系式即可.
本题考查菱形的性质,锐角三角函数的定义以及反比例函数图象上点值坐标的特征是解决问题的关键.
19.【答案】解:
;
.
【解析】按先算负整数指数幂、零指数幂、绝对值及三角函数,再算乘法,最后计算加减;
按先算三角函数,再算乘方,后算乘除,最后计算加减的顺序计算即可.
此题考查了实数混合运算的能力,关键是能确定正确的运算顺序,并能进行准确计算.
20.【答案】略
【解析】略
21.【答案】解:,可设,得,
,
,
解得,舍去,或,
,,
,
,
;
过点作于点,
,可设,则,
,
,
解得,舍,或,
,
.
【解析】本题是解直角三角形的应用,主要考查了解直角三角形,勾股定理,第二小题关键是构造直角三角形.
根据,可设,得,再由勾股定理列出的方程求得,进而由勾股定理求;
过点作于点,解直角三角形求得与,进而求得结果.
22.【答案】证明:点,、分别为,,的中点,
,,
四边形是平行四边形,
,
四边形是矩形;
解:,,,
,
即,
解得,
点为的中点,
,
,
即的长是.
【解析】根据三角形的中位线和矩形的判定方法可以证明结论成立;
根据,,可以得到的长,然后即可得到的长,再根据勾股定理,
即可求得的长.
本题考查矩形的判定、勾股定理、解直角三角形,解答本题的关键是明确矩形的判定方法,
利用数形结合的思想解答.
23.【答案】解:过作于,在点的正北方向上取点,在点的正北方向上取点,
由题意得:,,,海里,
,
在中,,
海里,
在中,,,
海里,
小时,
从处到达处需要小时.
【解析】此题考查了解直角三角形的应用方向角,熟练掌握锐角三角函数定义是解本题的关键.过作于,在点的正北方向上取点,在点的正北方向上取点,在直角三角形中,求出的长,在直角三角形中,利用锐角三角函数定义求出的长,进而求出所求时间即可.
24.【答案】解:延长交于点,
由题意得:
,米,米,
设米,
米,
在中,,
米,
在中,,
,
,
经检验:是原方程的根,
米,
拂云阁的高度约为米.
【解析】延长交于点,根据题意可得:,米,米,设米,在中,利用锐角三角函数的定义求出的长,然后在中,利用锐角三角函数的定义列出关于的方程,进行计算即可解答.
本题考查了解直角三角形的应用仰角俯角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
第1页,共1页
