全等三角形(SSS)[上学期]
文档属性
| 名称 | 全等三角形(SSS)[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 197.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2005-10-20 13:52:00 | ||
图片预览


文档简介
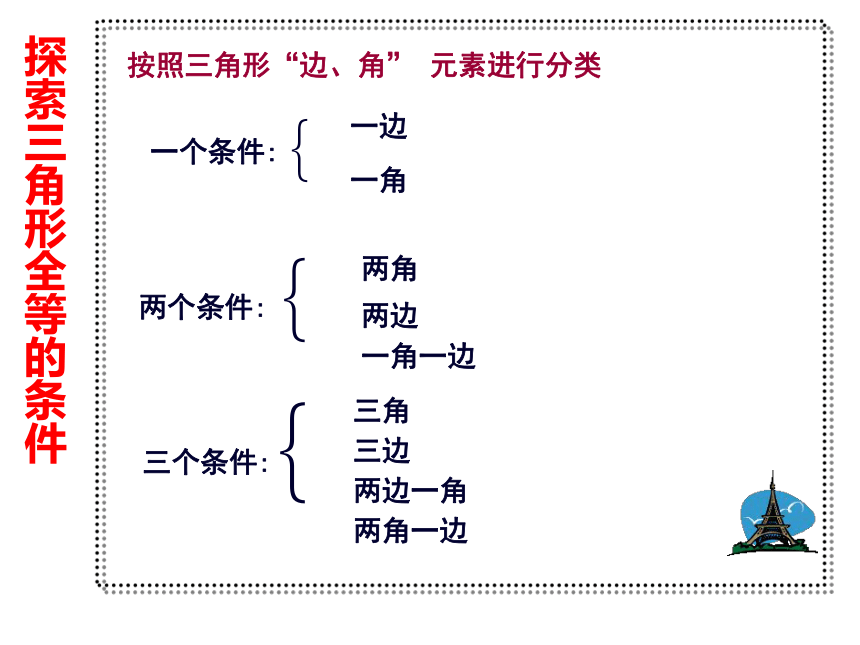
课件25张PPT。三角形全等的判定 1按照三角形“边、角” 元素进行分类探索三角形全等的条件
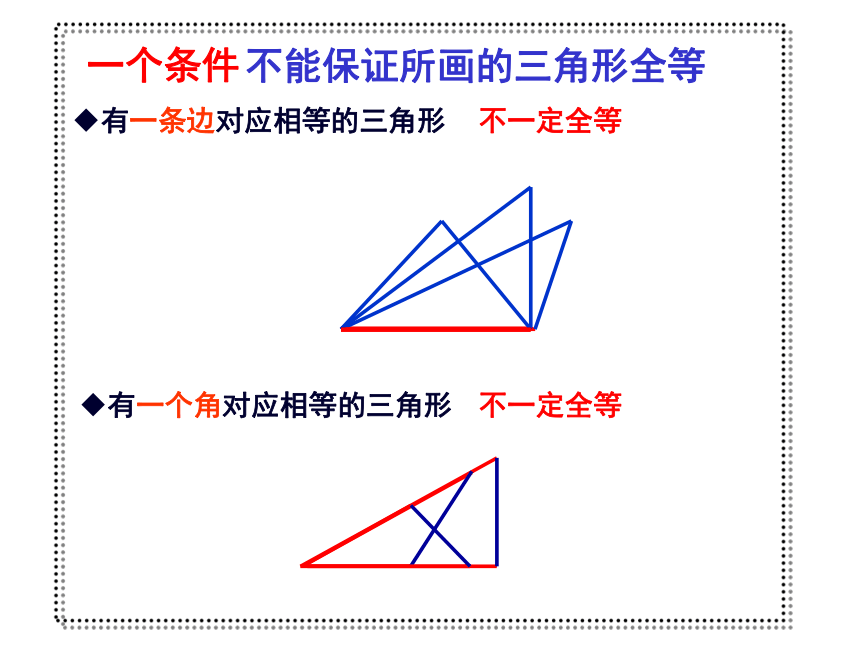
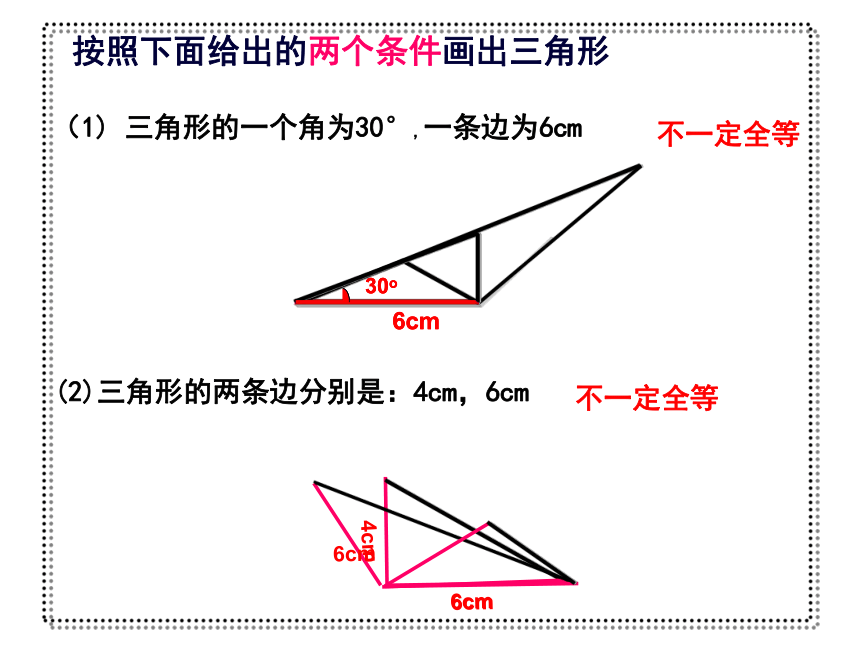
一个条件有一条边对应相等的三角形不一定全等有一个角对应相等的三角形不一定全等不能保证所画的三角形全等按照下面给出的两个条件画出三角形(1) 三角形的一个角为30°,一条边为6cm不一定全等(2)三角形的两条边分别是:4cm,6cm不一定全等(3)三角形的两个角分别是:30°,60° (4)已知三角形的三个角分别为30°,60°,90°不一定全等不一定全等只给出一个或两个条件时,都不能保证所画的三角形一定全等,并且三个内角对应相等的两个三角形也不一定全等。
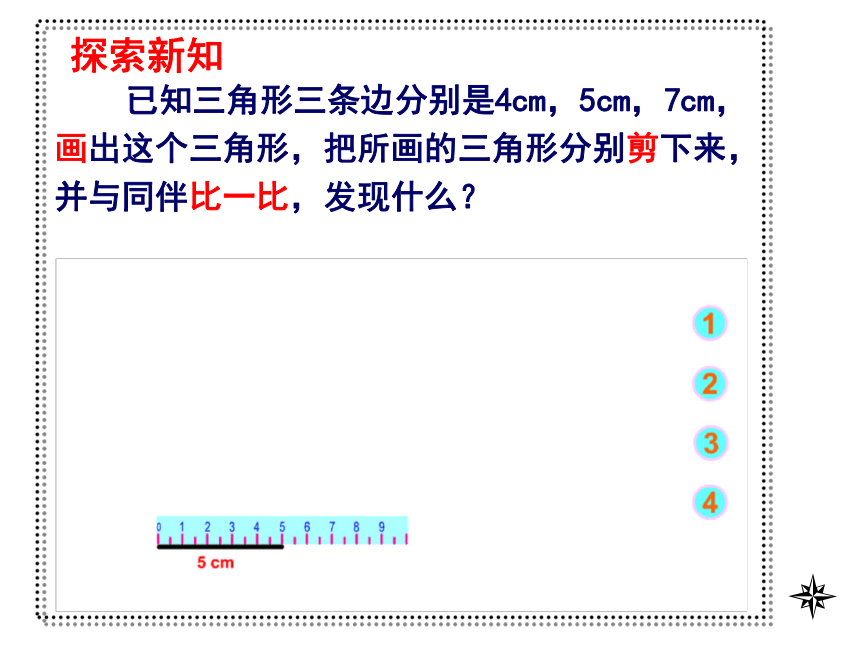
90°90°90° 已知三角形三条边分别是4cm,5cm,7cm,画出这个三角形,把所画的三角形分别剪下来,并与同伴比一比,发现什么?
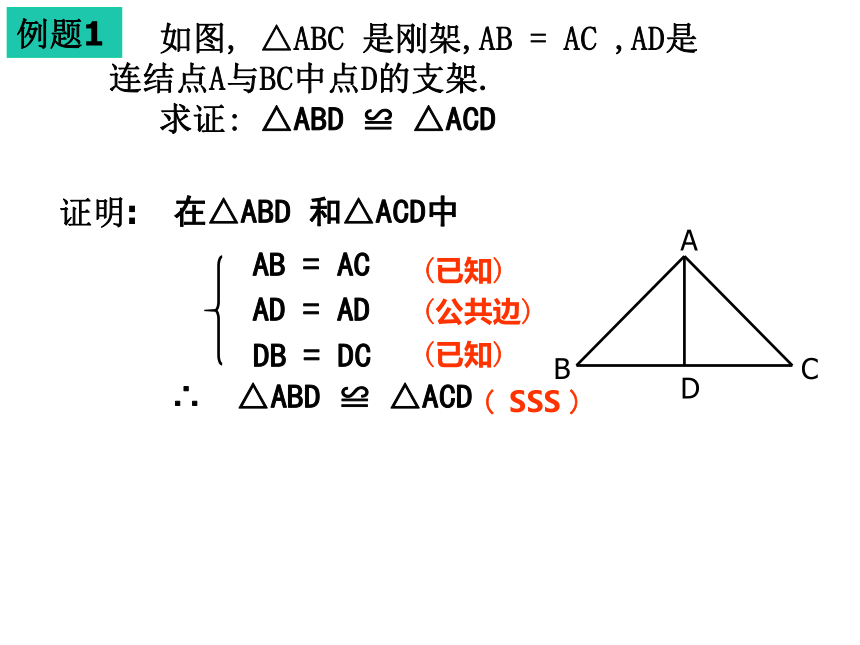
探索新知例题1 如图, △ABC 是刚架,AB = AC ,AD是
连结点A与BC中点D的支架.
求证: △ABD ≌ △ACD ACDB证明:在△ABD 和△ACD中AB = AC∴ △ABD ≌ △ACD(已知)(公共边)(已知)AD = ADDB = DC( SSS )例题1 如图, △ABC 是刚架,AB = AC ,AD是
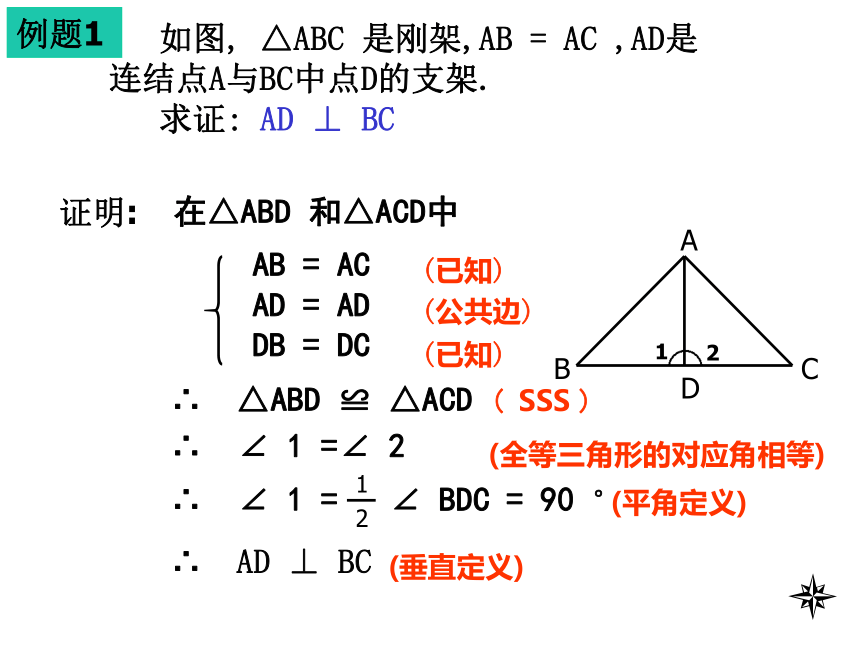
连结点A与BC中点D的支架.
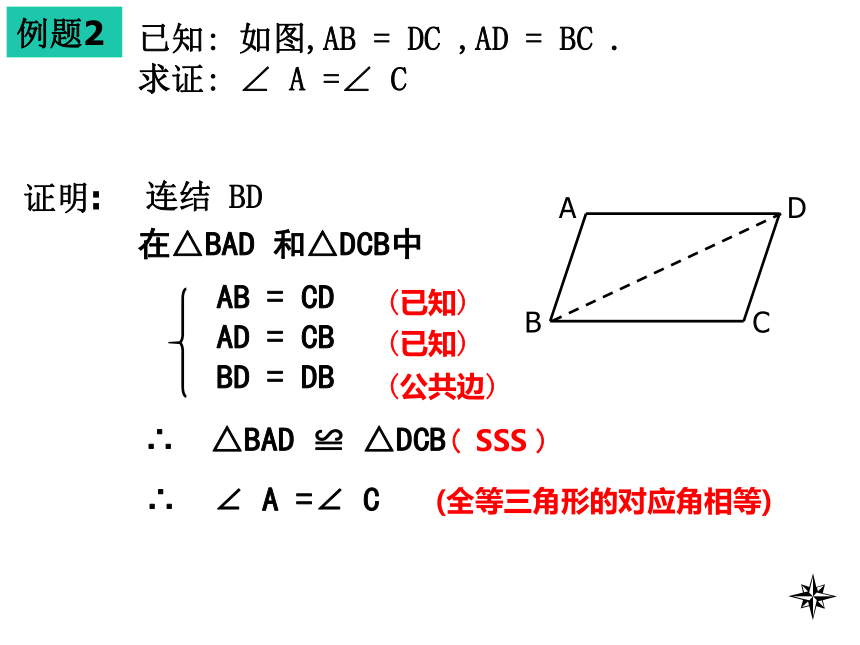
求证: AD ⊥ BCACD12B∴ ∠ 1 =∠ 2(全等三角形的对应角相等)∴ AD ⊥ BC(平角定义)(垂直定义)例题2已知: 如图,AB = DC ,AD = BC .
求证: ∠ A =∠ C证明:在△BAD 和△DCB中AB = CD
AD = CB
BD = DB∴ △BAD ≌ △DCB( SSS )∴ ∠ A =∠ C(全等三角形的对应角相等)ABCD连结 BD例题3已知: 如图,点B、E、C、F在同一直线上 ,
AB = DE ,AC = DF ,BE = CF .
求证: ∠ A =∠ D
CE证明:∴ △ABC ≌ △DEF ( SSS )∵ BE = CF∴ BC = EF∴ BE+EC = CF+CE练习 1如图已知: A、C、D、F四点在同一直线上,
AB = DE ,BC = EF ,AC = DF。
求证: AB ∥ DE分析:AB ∥ DE ∠ A =∠ D△ABC ≌ △DEF ( SSS )AB = DE BC = EF AC = DF证明:在△ABC 和△DEF中AB = DE
BC = EF
AC = DF∴ △ABC ≌ △DEF ( SSS )∴ AB ∥ DE ∴ ∠ A =∠ D甲(全等三角形对应角相等)(内错角相等两直线平行)如图已知: A、C、D、F四点在同一直线上,
AB = DE ,BC = EF ,AC = DF。
求证: AB ∥ DE练习 1 把图甲分别变换成图乙、图丙后,上题
的证明过程是否有变化? 甲练习 2练习2 把图甲分别变换成图乙、图丙后,上题
的证明过程是否有变化? ABCDEF练习 2 把图甲分别变换成图乙、图丙后,上题
的证明过程是否有变化? 练习 2 把图甲分别变换成图乙、图丙后,上题
的证明过程是否有变化? ABCDEF乙练习 2 把图甲分别变换成图乙、图丙后,上题
的证明过程是否有变化? ABCDEF乙练习 2 把图甲分别变换成图乙、图丙后,上题
的证明过程是否有变化? 练习 2 把图甲分别变换成图乙、图丙后,上题
的证明过程是否有变化? 练习 2 把图甲分别变换成图乙、图丙后,上题
的证明过程是否有变化? ABCDEF练习 2 把图甲分别变换成图乙、图丙后,上题
的证明过程是否有变化? ABCDEF丙练习2 把图甲分别变换成图乙、图丙后,上题
的证明过程是否有变化? BCBC△DCBBF=DC或 BD=FCBF=DC或 BD=FC知识的升华1.P103 作业题1,2题.
(做在作业本上)
2.预习下一节的内容并在课本上完成课后练习。
一个条件有一条边对应相等的三角形不一定全等有一个角对应相等的三角形不一定全等不能保证所画的三角形全等按照下面给出的两个条件画出三角形(1) 三角形的一个角为30°,一条边为6cm不一定全等(2)三角形的两条边分别是:4cm,6cm不一定全等(3)三角形的两个角分别是:30°,60° (4)已知三角形的三个角分别为30°,60°,90°不一定全等不一定全等只给出一个或两个条件时,都不能保证所画的三角形一定全等,并且三个内角对应相等的两个三角形也不一定全等。
90°90°90° 已知三角形三条边分别是4cm,5cm,7cm,画出这个三角形,把所画的三角形分别剪下来,并与同伴比一比,发现什么?
探索新知例题1 如图, △ABC 是刚架,AB = AC ,AD是
连结点A与BC中点D的支架.
求证: △ABD ≌ △ACD ACDB证明:在△ABD 和△ACD中AB = AC∴ △ABD ≌ △ACD(已知)(公共边)(已知)AD = ADDB = DC( SSS )例题1 如图, △ABC 是刚架,AB = AC ,AD是
连结点A与BC中点D的支架.
求证: AD ⊥ BCACD12B∴ ∠ 1 =∠ 2(全等三角形的对应角相等)∴ AD ⊥ BC(平角定义)(垂直定义)例题2已知: 如图,AB = DC ,AD = BC .
求证: ∠ A =∠ C证明:在△BAD 和△DCB中AB = CD
AD = CB
BD = DB∴ △BAD ≌ △DCB( SSS )∴ ∠ A =∠ C(全等三角形的对应角相等)ABCD连结 BD例题3已知: 如图,点B、E、C、F在同一直线上 ,
AB = DE ,AC = DF ,BE = CF .
求证: ∠ A =∠ D
CE证明:∴ △ABC ≌ △DEF ( SSS )∵ BE = CF∴ BC = EF∴ BE+EC = CF+CE练习 1如图已知: A、C、D、F四点在同一直线上,
AB = DE ,BC = EF ,AC = DF。
求证: AB ∥ DE分析:AB ∥ DE ∠ A =∠ D△ABC ≌ △DEF ( SSS )AB = DE BC = EF AC = DF证明:在△ABC 和△DEF中AB = DE
BC = EF
AC = DF∴ △ABC ≌ △DEF ( SSS )∴ AB ∥ DE ∴ ∠ A =∠ D甲(全等三角形对应角相等)(内错角相等两直线平行)如图已知: A、C、D、F四点在同一直线上,
AB = DE ,BC = EF ,AC = DF。
求证: AB ∥ DE练习 1 把图甲分别变换成图乙、图丙后,上题
的证明过程是否有变化? 甲练习 2练习2 把图甲分别变换成图乙、图丙后,上题
的证明过程是否有变化? ABCDEF练习 2 把图甲分别变换成图乙、图丙后,上题
的证明过程是否有变化? 练习 2 把图甲分别变换成图乙、图丙后,上题
的证明过程是否有变化? ABCDEF乙练习 2 把图甲分别变换成图乙、图丙后,上题
的证明过程是否有变化? ABCDEF乙练习 2 把图甲分别变换成图乙、图丙后,上题
的证明过程是否有变化? 练习 2 把图甲分别变换成图乙、图丙后,上题
的证明过程是否有变化? 练习 2 把图甲分别变换成图乙、图丙后,上题
的证明过程是否有变化? ABCDEF练习 2 把图甲分别变换成图乙、图丙后,上题
的证明过程是否有变化? ABCDEF丙练习2 把图甲分别变换成图乙、图丙后,上题
的证明过程是否有变化? BCBC△DCBBF=DC或 BD=FCBF=DC或 BD=FC知识的升华1.P103 作业题1,2题.
(做在作业本上)
2.预习下一节的内容并在课本上完成课后练习。
