全等三角形的探索(一)[上学期]
文档属性
| 名称 | 全等三角形的探索(一)[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2005-10-20 13:58:00 | ||
图片预览




文档简介
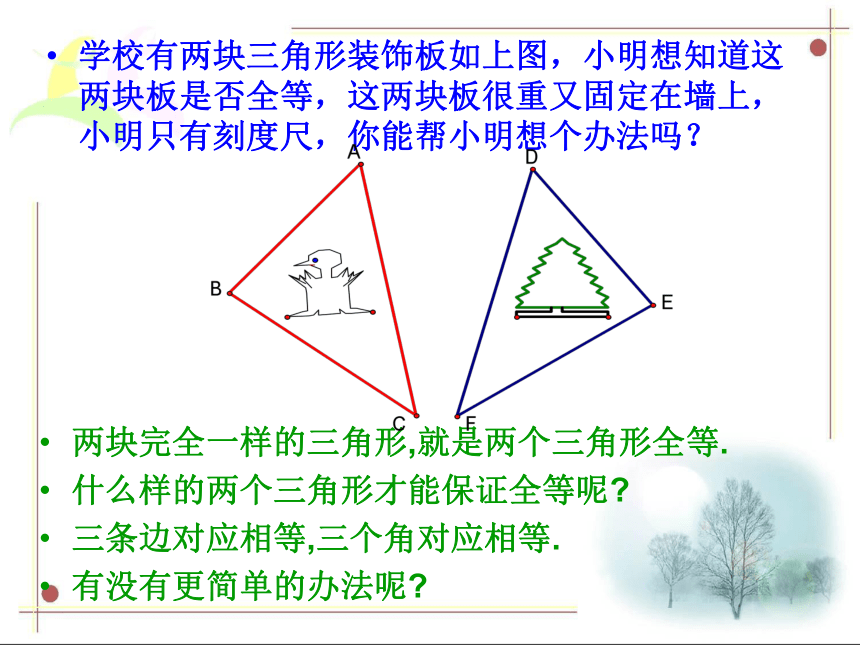
课件20张PPT。探索三角形全等的条件(1)重庆市綦江古南中学叶含其两块完全一样的三角形,就是两个三角形全等.
什么样的两个三角形才能保证全等呢?
三条边对应相等,三个角对应相等.
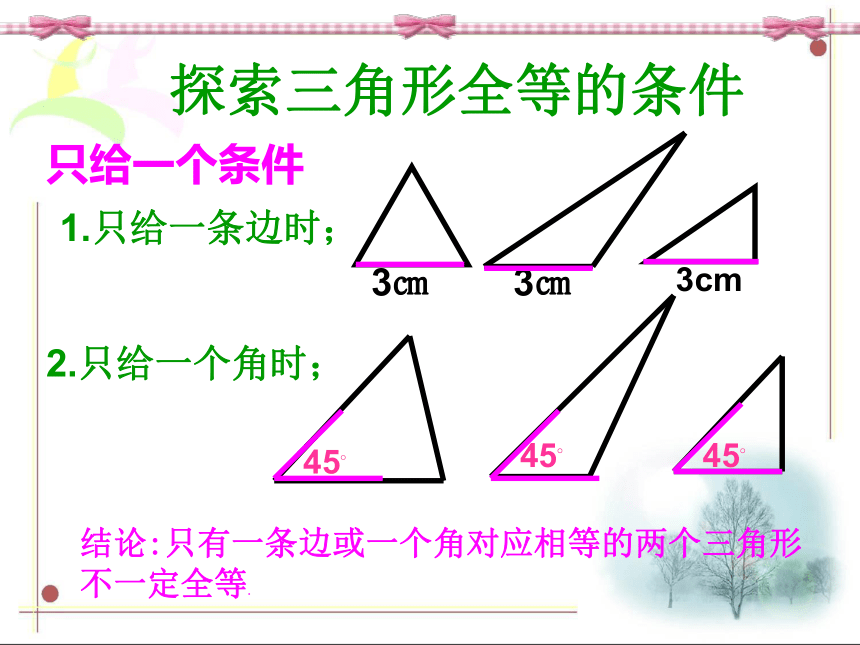
有没有更简单的办法呢?学校有两块三角形装饰板如上图,小明想知道这两块板是否全等,这两块板很重又固定在墙上,小明只有刻度尺,你能帮小明想个办法吗?探索三角形全等的条件1.只给一条边时;3㎝3㎝只给一个条件45?45?2.只给一个角时;3cm45?结论:只有一条边或一个角对应相等的两个三角形不一定全等.如果给出两个条件画三角形,
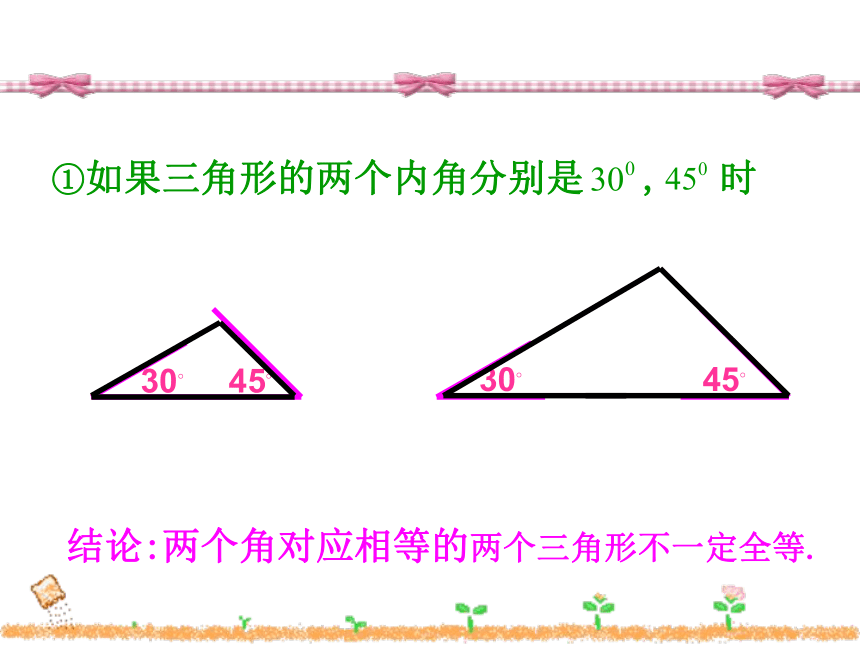
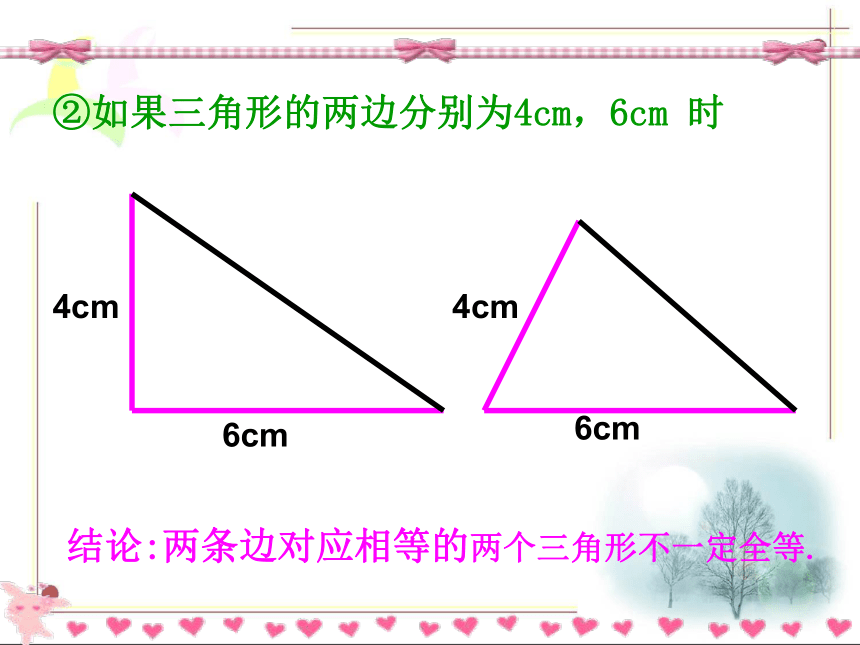
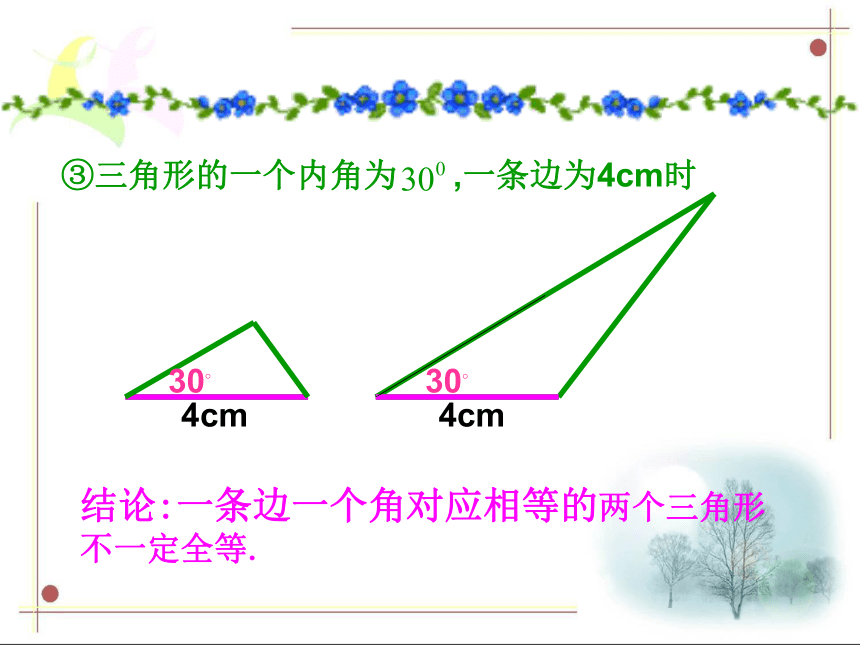
你能说出有哪几种可能的情况?①两角;③一边一角。②两边;①如果三角形的两个内角分别是 , 时结论:两个角对应相等的两个三角形不一定全等.②如果三角形的两边分别为4cm,6cm 时6cm6cm4cm4cm结论:两条边对应相等的两个三角形不一定全等. ③三角形的一个内角为 ,一条边为4cm时4cm4cm30?30?结论:一条边一个角对应相等的两个三角形不一定全等.两个条件
①两角;
②两边;
③一边一角。结论:只给出一个或两个条件时,都不能保证所画的三角形一定全等。一个条件
①一角;
②一边;你能得到什么结论吗?如果给出三个条件画三角形,
你能说出有哪几种可能的情况?①三角;②三边;③两边一角;④两角一边。 ①三个角:给出三个条件300700800300700800如30 ,70 ,80, 它们
一定全等吗?结论:三个角对应相等的两个三角形不一定全等.2、画出一个三角形,使它的三边长分别为3cm、 4cm、6cm ,把你画的三角形与小组内画的进行比较,它们一定全等吗?画法: 1.画线段AB=3㎝;2.分别以A、B为圆心,4㎝和6㎝长为半径画弧,两弧交于点C;3. 连接线段AC、BC.结论:三边对应相等的两个三角形全等.可简写为边边边或SSS思考:你能用三角形的稳定性来说明SSS公理吗?如何用符号语言来表达呢?在△ABC与△DEF中AB=DE
AC=DF
BC=EF∴△ABC≌△DEF(SSS)例1.如图, △ABC是一个钢架,AB=AC,AD是连接A与BC中点D的支架,求证: △ABD≌△ACD A C B D分析:要证明两个三角形全等,需要那些条件?证明:∵D是BC的中点∴BD=CD在△ABD与△ACD中AB=AC(已知)BD=CD(已证)AD=AD(公共边)∴△ABD≌△ACD(SSS)练习1。已知:如图,AB=AD,BC=CD, 求证:(1)△ABC≌ (2)∠B=∠D ABCD△ADCACAC ( ) ≌AB=AD ( )
BC=CD ( )∴ △ABC △ADC(SSS)证明:在△ABC和△ADC中=已知已知 公共边∴ ∠B=∠D (全等三角形的对应角相等)BCBC△DCBBF=DC或 BD=FCABCD练习2。解: △ABC≌△DCB
理由如下:
AB = CD
AC = BD
=
△ABD ≌ ( ) S S S (1)如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。 (2)如图,D、F是线段BC上的两点,
AB=CE,AF=DE,要使△ABF≌△ECD ,
还需要条件
AE B D F C
练习3。如图,在四边形ABCD中,AB=CD,AD=CB,则∠ A= ∠ C.请说明理由 DABC证明:在△ABD和△CDB中AB=CDAD=CBBD=DB∴△ABD≌△ACD(SSS)(已知)(已知)(公共边)∴ ∠ A= ∠ C (全等三角形的对应角相等)你能说明AB∥CD,AD∥BC吗?练习:1、如图,AB=AC,BD=CD,BH=CH,图中有几组全等的三角形?它们全等的条件是什么?HDCBA解:有三组。
在△ABH和△ACH中 ∵AB=AC,BH=CH,AH=AH ∴△ABH≌△ACH(SSS);∵BD=CD,BH=CH,DH=DH
∴△DBH≌△DCH(SSS) 在△ABH和△ACH中
∵AB=AC,BD=CD,AD=AD ∴△ABD≌△ACD(SSS);在△ABH和△ACH中解:①∵E、F分别是AB,CD的中点( )又∵AB=CD∴AE=CF在△ADE与△CBF中AE==∴△ADE≌△CBF ( )∴AE= AB CF= CD( )补充练习:如图,已知AB=CD,AD=CB,E、F分别是AB,CD的中点,且DE=BF,说出下列判断成立的理由.①△ADE≌△CBF②∠A=∠C线段中点的定义CFADABCDSSS△ADE≌△CBF全等三角形对应角相等已知CB② ∵∴ ∠A=∠C ( )=作业P96通过这节课的学习,你有什么收获?再见
什么样的两个三角形才能保证全等呢?
三条边对应相等,三个角对应相等.
有没有更简单的办法呢?学校有两块三角形装饰板如上图,小明想知道这两块板是否全等,这两块板很重又固定在墙上,小明只有刻度尺,你能帮小明想个办法吗?探索三角形全等的条件1.只给一条边时;3㎝3㎝只给一个条件45?45?2.只给一个角时;3cm45?结论:只有一条边或一个角对应相等的两个三角形不一定全等.如果给出两个条件画三角形,
你能说出有哪几种可能的情况?①两角;③一边一角。②两边;①如果三角形的两个内角分别是 , 时结论:两个角对应相等的两个三角形不一定全等.②如果三角形的两边分别为4cm,6cm 时6cm6cm4cm4cm结论:两条边对应相等的两个三角形不一定全等. ③三角形的一个内角为 ,一条边为4cm时4cm4cm30?30?结论:一条边一个角对应相等的两个三角形不一定全等.两个条件
①两角;
②两边;
③一边一角。结论:只给出一个或两个条件时,都不能保证所画的三角形一定全等。一个条件
①一角;
②一边;你能得到什么结论吗?如果给出三个条件画三角形,
你能说出有哪几种可能的情况?①三角;②三边;③两边一角;④两角一边。 ①三个角:给出三个条件300700800300700800如30 ,70 ,80, 它们
一定全等吗?结论:三个角对应相等的两个三角形不一定全等.2、画出一个三角形,使它的三边长分别为3cm、 4cm、6cm ,把你画的三角形与小组内画的进行比较,它们一定全等吗?画法: 1.画线段AB=3㎝;2.分别以A、B为圆心,4㎝和6㎝长为半径画弧,两弧交于点C;3. 连接线段AC、BC.结论:三边对应相等的两个三角形全等.可简写为边边边或SSS思考:你能用三角形的稳定性来说明SSS公理吗?如何用符号语言来表达呢?在△ABC与△DEF中AB=DE
AC=DF
BC=EF∴△ABC≌△DEF(SSS)例1.如图, △ABC是一个钢架,AB=AC,AD是连接A与BC中点D的支架,求证: △ABD≌△ACD A C B D分析:要证明两个三角形全等,需要那些条件?证明:∵D是BC的中点∴BD=CD在△ABD与△ACD中AB=AC(已知)BD=CD(已证)AD=AD(公共边)∴△ABD≌△ACD(SSS)练习1。已知:如图,AB=AD,BC=CD, 求证:(1)△ABC≌ (2)∠B=∠D ABCD△ADCACAC ( ) ≌AB=AD ( )
BC=CD ( )∴ △ABC △ADC(SSS)证明:在△ABC和△ADC中=已知已知 公共边∴ ∠B=∠D (全等三角形的对应角相等)BCBC△DCBBF=DC或 BD=FCABCD练习2。解: △ABC≌△DCB
理由如下:
AB = CD
AC = BD
=
△ABD ≌ ( ) S S S (1)如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。 (2)如图,D、F是线段BC上的两点,
AB=CE,AF=DE,要使△ABF≌△ECD ,
还需要条件
AE B D F C
练习3。如图,在四边形ABCD中,AB=CD,AD=CB,则∠ A= ∠ C.请说明理由 DABC证明:在△ABD和△CDB中AB=CDAD=CBBD=DB∴△ABD≌△ACD(SSS)(已知)(已知)(公共边)∴ ∠ A= ∠ C (全等三角形的对应角相等)你能说明AB∥CD,AD∥BC吗?练习:1、如图,AB=AC,BD=CD,BH=CH,图中有几组全等的三角形?它们全等的条件是什么?HDCBA解:有三组。
在△ABH和△ACH中 ∵AB=AC,BH=CH,AH=AH ∴△ABH≌△ACH(SSS);∵BD=CD,BH=CH,DH=DH
∴△DBH≌△DCH(SSS) 在△ABH和△ACH中
∵AB=AC,BD=CD,AD=AD ∴△ABD≌△ACD(SSS);在△ABH和△ACH中解:①∵E、F分别是AB,CD的中点( )又∵AB=CD∴AE=CF在△ADE与△CBF中AE==∴△ADE≌△CBF ( )∴AE= AB CF= CD( )补充练习:如图,已知AB=CD,AD=CB,E、F分别是AB,CD的中点,且DE=BF,说出下列判断成立的理由.①△ADE≌△CBF②∠A=∠C线段中点的定义CFADABCDSSS△ADE≌△CBF全等三角形对应角相等已知CB② ∵∴ ∠A=∠C ( )=作业P96通过这节课的学习,你有什么收获?再见
