17.3 一次函数 复习课件(共14张PPT)
文档属性
| 名称 | 17.3 一次函数 复习课件(共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 879.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-19 20:35:30 | ||
图片预览





文档简介
(共14张PPT)
华师大版八年级下册
一次函数复习课
直角坐标系的建立
通常称为笛卡儿直角坐标系,它是以法国哲学家、数学家和自然科学家笛卡儿的名字命名的。
在平面内画两条互相垂直的数轴,组成平面直角坐标系
①水平的轴叫做x轴或横轴, 取向右为正方向
②铅直的数轴叫做y轴或纵轴,取向上为正方向
③两轴的交点是原点O
建立了平面直角坐标系后,两条坐标轴把平面分四个区域,分别称为第一、二、三、四象限,坐标轴不属于任何一个象限
点找坐标,坐标找点
在平面直角坐标系中,任意一点都可以用对有序实数来表示
①从点P分别向x轴和y轴作垂线,垂足分别为M和N.
②点P在x轴对应的数2,称为点P的横坐标
③点P在y轴上对应的数为3,称为P点的纵坐标
∴点P的坐标(2,3)
有序实数对---先横后纵
(2,3)
B
A
D
A(-3,2)
B(-5,0)
D(0,-3)
O(-3,2)
一、知识要点:
1、一次函数的概念:函数y=_______(k、b为常数,k______)叫做一次函数。当b_____时,函数y=____(k____)叫做正比例函数。
★理解一次函数概念应注意下面两点:
⑴、解析式中自变量x的次数是___次,
⑵、比例系数_____。
2、正比例函数y=kx(k≠0)的图象是过点(_____),(______)的_________。
3、一次函数y=kx+b(k≠0)的图象是过点(0,___),(____,0)的__________。
kx +b
≠0 =0
kx ≠0
1
K≠0
0,0 1,k 一条直线
b
一条直线
4、直线y=kx+b(k≠0)的图象可以由y=kx(k≠0)的图象沿_________平移得到。
Y轴上下
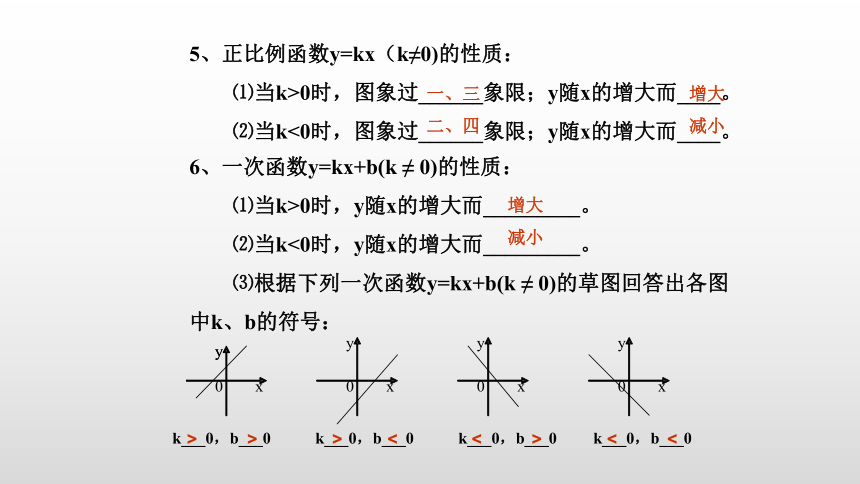
5、正比例函数y=kx(k≠0)的性质:
⑴当k>0时,图象过______象限;y随x的增大而____。
⑵当k<0时,图象过______象限;y随x的增大而____。
6、一次函数y=kx+b(k ≠ 0)的性质:
⑴当k>0时,y随x的增大而_________。
⑵当k<0时,y随x的增大而_________。
⑶根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图
中k、b的符号:
k___0,b___0 k___0,b___0 k___0,b___0 k___0,b___0
一、三 增大
二、四 减小
增大
减小
> > > <
< > < <
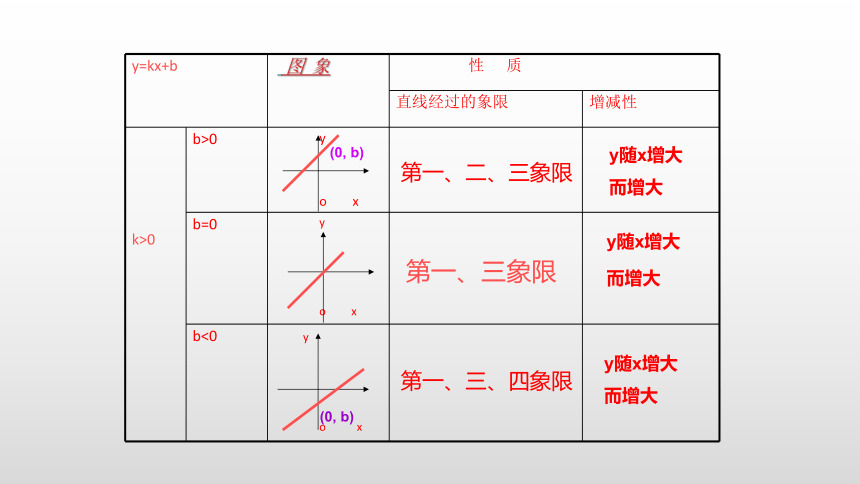
y=kx+b 图 象 性 质
直线经过的象限 增减性
k>0 b>0 y o x
b=0 y o x
b<0 y o x
第一、三象限
y随x增大
而增大
第一、二、三象限
y随x增大
而增大
第一、三、四象限
y随x增大
而增大
(0, b)
(0, b)
y=kx+b 图 象 性 质
直线经过的象限 增减性
k<0 b>0 y o x
b=0 y o x
b<0 y o x
第二、四象限
y随x增大
而减小
第一、二、四象限
y随x增大
而减小
第二、三、四象限
y随x增大
而减小
(0, b)
(o, b)
待定系数法:
先设待求的函数表达式(其中含有未知的系数)再根据条件列出方程或方程组,求出未知系数,从而得到所求结果的方法,叫做待定系数法。
用待定系数法解题一般分为几步?
一设、二列、三解、四还原:
1. 设一次函数的一般形式y=kx+b(k≠0);
2. 根据已知条件列出关于k、b的二元一次方程组;
3. 解这个方程组,求出k、b;
4. 将已经求出的 k、b的值代入解析式.
1.下列函数中,是一次函数的是_________.
y=8x2 ,y=x+1 , y= , y= ,y=-3x.
8
x
x +1
1
2.当m ____时,函数 是一次函数.
热身运动
y=x+1
y=-3x
≠-3
3. 一次函数y=x+1的图像大致是( ).
4.一次函数y=-x+1的图像不通过第___象限。
D
三
5.(1)对于函数y=5x+6,y的值随x值的减小而______.
(2)对于函数 , y的值随x值的____而增大
减小
减小
x
y
o
x
y
o
x
y
o
x
y
o
-1
1
1
1
-1
-1
B
A
C
D
提高练习
已知y与x-3成正比例,当x=4时,y=3. (1)写出y与x之间的函数表达式;
(2)y与x之间是什么函数关系?
(3)求x=2.5时,y的值.
1.变化使我们成熟,但它首先使我们痛苦。人生中最重要的变化,一定伴随着大的焦灼和忧虑。 ——毕淑敏
2.情况是在不断地变化,要使自己的思想适应新的情况,就得学习。 ——毛泽东
3.彼一时,此一时也。 ——孟子
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
华师大版八年级下册
一次函数复习课
直角坐标系的建立
通常称为笛卡儿直角坐标系,它是以法国哲学家、数学家和自然科学家笛卡儿的名字命名的。
在平面内画两条互相垂直的数轴,组成平面直角坐标系
①水平的轴叫做x轴或横轴, 取向右为正方向
②铅直的数轴叫做y轴或纵轴,取向上为正方向
③两轴的交点是原点O
建立了平面直角坐标系后,两条坐标轴把平面分四个区域,分别称为第一、二、三、四象限,坐标轴不属于任何一个象限
点找坐标,坐标找点
在平面直角坐标系中,任意一点都可以用对有序实数来表示
①从点P分别向x轴和y轴作垂线,垂足分别为M和N.
②点P在x轴对应的数2,称为点P的横坐标
③点P在y轴上对应的数为3,称为P点的纵坐标
∴点P的坐标(2,3)
有序实数对---先横后纵
(2,3)
B
A
D
A(-3,2)
B(-5,0)
D(0,-3)
O(-3,2)
一、知识要点:
1、一次函数的概念:函数y=_______(k、b为常数,k______)叫做一次函数。当b_____时,函数y=____(k____)叫做正比例函数。
★理解一次函数概念应注意下面两点:
⑴、解析式中自变量x的次数是___次,
⑵、比例系数_____。
2、正比例函数y=kx(k≠0)的图象是过点(_____),(______)的_________。
3、一次函数y=kx+b(k≠0)的图象是过点(0,___),(____,0)的__________。
kx +b
≠0 =0
kx ≠0
1
K≠0
0,0 1,k 一条直线
b
一条直线
4、直线y=kx+b(k≠0)的图象可以由y=kx(k≠0)的图象沿_________平移得到。
Y轴上下
5、正比例函数y=kx(k≠0)的性质:
⑴当k>0时,图象过______象限;y随x的增大而____。
⑵当k<0时,图象过______象限;y随x的增大而____。
6、一次函数y=kx+b(k ≠ 0)的性质:
⑴当k>0时,y随x的增大而_________。
⑵当k<0时,y随x的增大而_________。
⑶根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图
中k、b的符号:
k___0,b___0 k___0,b___0 k___0,b___0 k___0,b___0
一、三 增大
二、四 减小
增大
减小
> > > <
< > < <
y=kx+b 图 象 性 质
直线经过的象限 增减性
k>0 b>0 y o x
b=0 y o x
b<0 y o x
第一、三象限
y随x增大
而增大
第一、二、三象限
y随x增大
而增大
第一、三、四象限
y随x增大
而增大
(0, b)
(0, b)
y=kx+b 图 象 性 质
直线经过的象限 增减性
k<0 b>0 y o x
b=0 y o x
b<0 y o x
第二、四象限
y随x增大
而减小
第一、二、四象限
y随x增大
而减小
第二、三、四象限
y随x增大
而减小
(0, b)
(o, b)
待定系数法:
先设待求的函数表达式(其中含有未知的系数)再根据条件列出方程或方程组,求出未知系数,从而得到所求结果的方法,叫做待定系数法。
用待定系数法解题一般分为几步?
一设、二列、三解、四还原:
1. 设一次函数的一般形式y=kx+b(k≠0);
2. 根据已知条件列出关于k、b的二元一次方程组;
3. 解这个方程组,求出k、b;
4. 将已经求出的 k、b的值代入解析式.
1.下列函数中,是一次函数的是_________.
y=8x2 ,y=x+1 , y= , y= ,y=-3x.
8
x
x +1
1
2.当m ____时,函数 是一次函数.
热身运动
y=x+1
y=-3x
≠-3
3. 一次函数y=x+1的图像大致是( ).
4.一次函数y=-x+1的图像不通过第___象限。
D
三
5.(1)对于函数y=5x+6,y的值随x值的减小而______.
(2)对于函数 , y的值随x值的____而增大
减小
减小
x
y
o
x
y
o
x
y
o
x
y
o
-1
1
1
1
-1
-1
B
A
C
D
提高练习
已知y与x-3成正比例,当x=4时,y=3. (1)写出y与x之间的函数表达式;
(2)y与x之间是什么函数关系?
(3)求x=2.5时,y的值.
1.变化使我们成熟,但它首先使我们痛苦。人生中最重要的变化,一定伴随着大的焦灼和忧虑。 ——毕淑敏
2.情况是在不断地变化,要使自己的思想适应新的情况,就得学习。 ——毛泽东
3.彼一时,此一时也。 ——孟子
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
