第24章 圆单元质量评估试题（含解析）

中小学教育资源及组卷应用平台
第24章 圆单元质量评估(时间:90分钟　满分:120分)
一、选择题(每小题3分,共30分)
1.如图所示,如果AB为☉O的直径,弦CD⊥AB,垂足为E,那么下列结论中,错误的是 (　　)
　　　　　　　　　　　　　　　　　　
A.CE=DE B.弧BC=弧BD
C.∠BAC=∠BAD D.AC>AD
2.如图所示,四边形ABCD内接于☉O,如果它的一个外角∠DCE=64°,那么∠BOD等于 (　　)
A.128° B.100°
C.64° D.32°
3.已知☉O的半径为6,A为线段PO的中点,当OP=10时,点A与☉O的位置关系为 (　　)
A.在圆上 B.在圆外
C.在圆内 D.不确定
4.如图所示,EB为半圆O的直径,点A在EB的延长线上,AD切半圆O于点D,BC⊥AD于点C,AB=2,半圆O的半径为2,则BC的长为 (　　)
A.2 B.1 C.1.5 D.0.5
5.半径为R的圆内接正三角形的面积是 (　　)
A.R2 B.πR2
C.R2 D.R2
6.如图所示,已知☉O的半径OA=6,∠AOB=90°,则∠AOB所对的弧AB的长为 (　　)
A.2π B.3π
C.6π D.12π
7.圆内接四边形ABCD,∠A,∠B,∠C的度数之比为3∶4∶6,则∠D的度数为 (　　)
A.60° B.80°
C.100° D.120°
8.如图所示,若☉O的半径长是4 cm,圆外一点A与☉O上各点的最远距离是12 cm,则自A点所引☉O的切线AD长为 (　　)
A.16 cm B.4 cm
C.4 cm D.4 cm
9.如图所示,以等腰直角三角形ABC两锐角顶点A,B为圆心作等圆,☉A与☉B恰好外切,如果AC=2,那么图中两个扇形(阴影部分)的面积之和为 (　　)
A. B. C. D.π
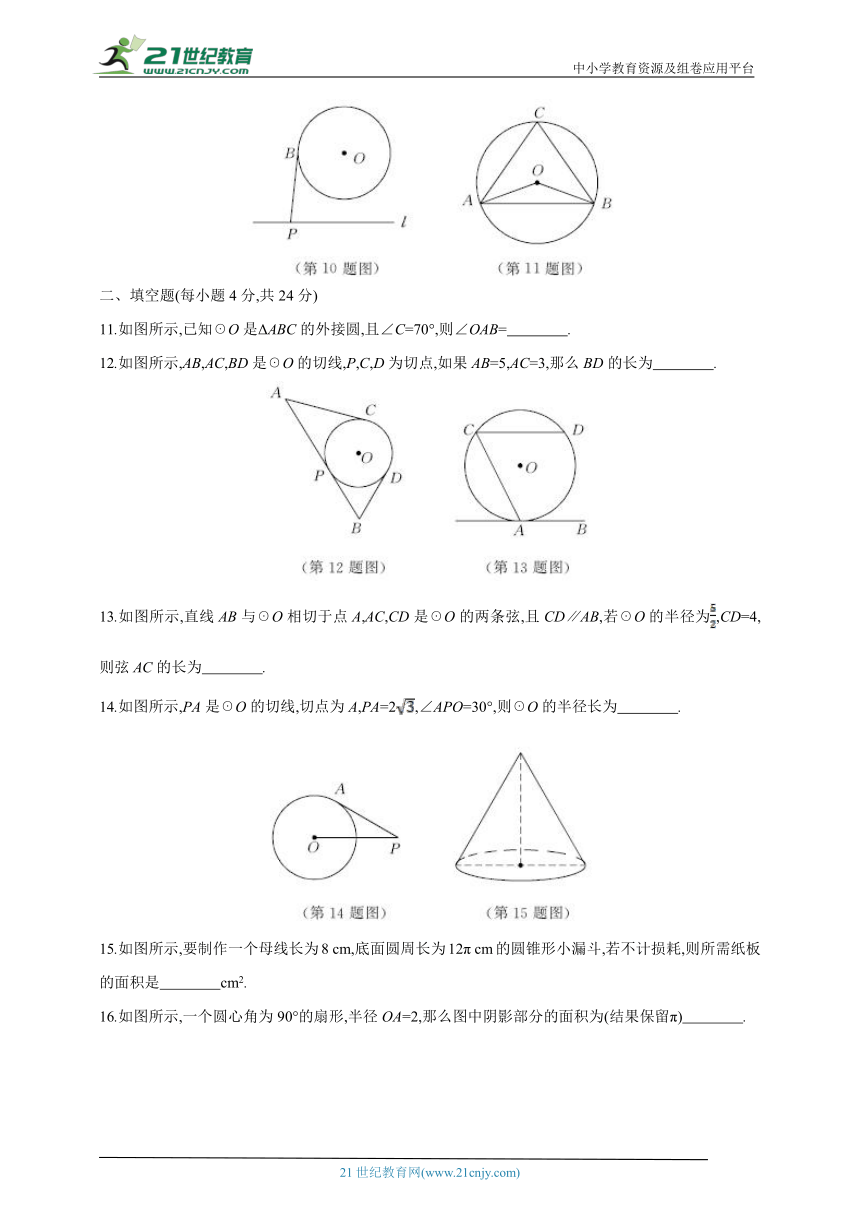
10.如图所示,☉O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点,PB切☉O于点B,则PB的最小值是 (　　)
A. B.
C.3 D.2
二、填空题(每小题4分,共24分)
11.如图所示,已知☉O是ΔABC的外接圆,且∠C=70°,则∠OAB=　　　　.
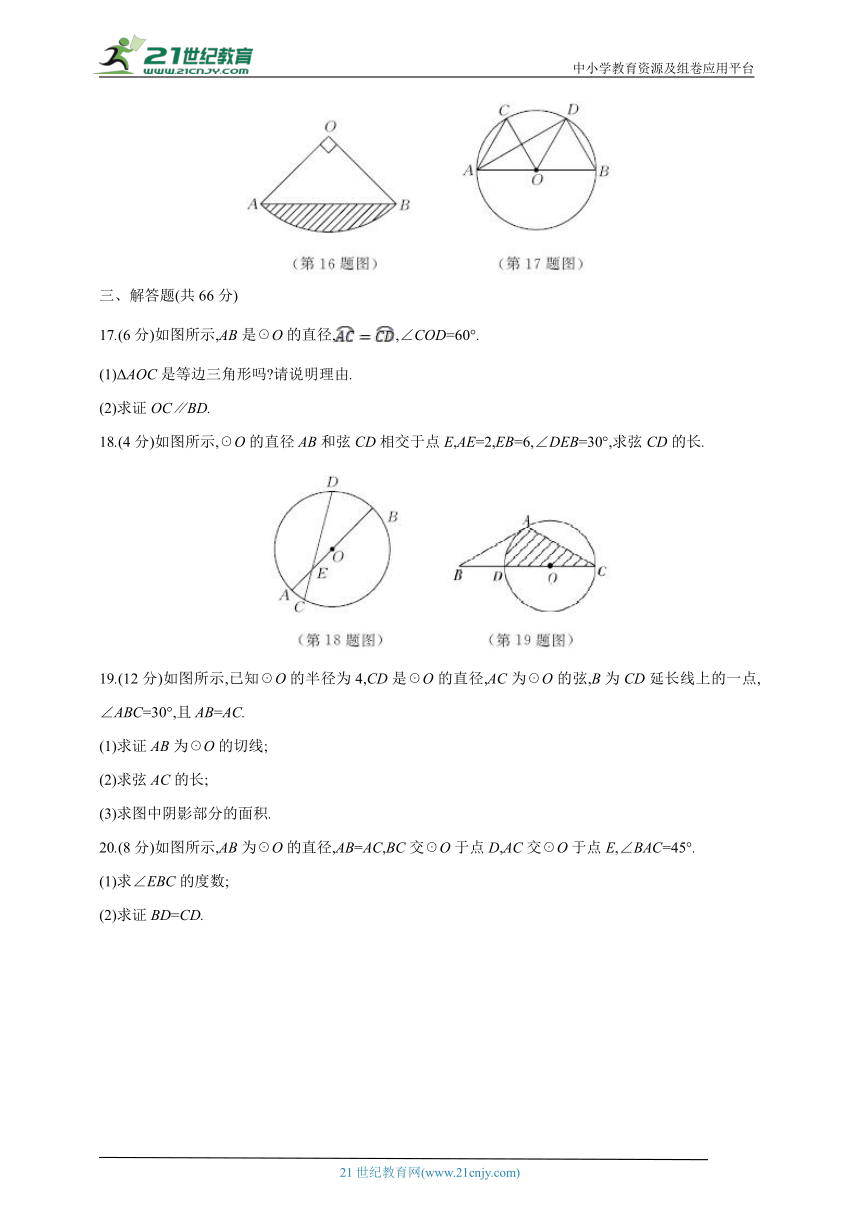
12.如图所示,AB,AC,BD是☉O的切线,P,C,D为切点,如果AB=5,AC=3,那么BD的长为　　　　.
13.如图所示,直线AB与☉O相切于点A,AC,CD是☉O的两条弦,且CD∥AB,若☉O的半径为,CD=4,则弦AC的长为　　　　.
14.如图所示,PA是☉O的切线,切点为A,PA=2,∠APO=30°,则☉O的半径长为　　　　.
15.如图所示,要制作一个母线长为8 cm,底面圆周长为12π cm的圆锥形小漏斗,若不计损耗,则所需纸板的面积是　　　　cm2.
16.如图所示,一个圆心角为90°的扇形,半径OA=2,那么图中阴影部分的面积为(结果保留π)　　　　.
三、解答题(共66分)
17.(6分)如图所示,AB是☉O的直径,,∠COD=60°.
(1)ΔAOC是等边三角形吗 请说明理由.
(2)求证OC∥BD.
18.(4分)如图所示,☉O的直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD的长.
19.(12分)如图所示,已知☉O的半径为4,CD是☉O的直径,AC为☉O的弦,B为CD延长线上的一点,∠ABC=30°,且AB=AC.
(1)求证AB为☉O的切线;
(2)求弦AC的长;
(3)求图中阴影部分的面积.
20.(8分)如图所示,AB为☉O的直径,AB=AC,BC交☉O于点D,AC交☉O于点E,∠BAC=45°.
(1)求∠EBC的度数;
(2)求证BD=CD.
21.(6分)如图所示,在平面直角坐标系中,点P在第一象限,☉P与x轴相切于点Q,与y轴交于点M(0,2),N(0,8)两点,求点P的坐标.
22.(8分)已知ΔABC内接于☉O,过点A作直线EF.
(1)如图(1)所示,AB为直径,要使EF为☉O的切线,求还需添加的条件(只需写出两种情况);
(2)如图(2)所示,AB是非直径的弦,∠CAE=∠B,求证EF是☉O的切线.
23.(10分)如图所示,AB是☉O的直径,AC是弦,直线EF是过点C的☉O的切线,AD⊥EF于点D.
(1)求证∠BAC=∠CAD;
(2)若∠B=30°,AB=12,求的长.
24.(12分)如图所示,☉O的直径AB=4,点P是AB延长线上的一点,过P点作☉O的切线,切点为C,连接AC.
(1)若∠CPA=30°,求PC的长;
(2)若点P在AB的延长线上运动,∠CPA的平分线交AC于点M,你认为∠CMP的大小是否发生变化 若变化,请说明理由;若不变化,求出∠CMP的大小.
【答案与解析】
1.D(解析:根据垂径定理得到CE=DE,弧BC=弧BD,所以选项A,B正确;由前面得到的结论,再根据圆周角定理可得∠BAC=∠BAD,所以选项C正确;由前面证明得到AB是线段CD的垂直平分线,再根据垂直平分线的性质得到AC=AD,所以选项D错误.故选D.)
2.A(解析:∵∠DCE=64°,∴∠BCD=116°,∵四边形ABCD内接于☉O,∴∠A+∠DCB=180°,∴∠A=64°,∴∠BOD=2∠A=128°.故选A.)
3.C(解析:∵点A为OP的中点,∴OA=OP÷2=5<6,∴点A在☉O内部.)
4.B(解析:如图所示,连接OD.∵AD是切线,点D是切点,BC⊥AD,∴∠ODA=∠ACB=90°,∴BC∥OD.∵AB=OB=2,∴点B是AO的中点,∴BC=OD=1.)
5.D(解析:如图所示,过O作OD⊥BC于D,∵三角形ABC是正三角形,∴∠BOC=2∠A=120°.∵OB=OC,∴∠BOD=×120°=60°,∴∠OBD=30°,∵OB=R,∴OD=R,由勾股定理得BD=R,∴BC=2BD=2×R=R,∴SΔBOC=×BC×OD=R×R=R2,∴SΔABC=3×R2=R2.故选D.)
6.B(解析:根据弧长计算公式可得l==3π.故选B.)
7.C(解析:∵∠A∶∠B∶∠C=3∶4∶6,∴设∠A的度数为3x,则∠B,∠C的度数分别为4x,6x,∵内接四边形的对角互补,∴3x+6x=180°,∴x=20°,∴∠A=60°,∠B=80°,∠C=120°,∵∠A+∠B+∠C+∠D=360°,∴∠D=100°.故选C.)
8.B(解析:根据题意得AC=12 cm,则OA=12-4=8(cm).连接OD,∵AD是圆的切线,∴∠ADO=90°,由勾股定理可得AD==4(cm).故选B.)
9.B(解析:设∠A=x°,∠B=y°,∵☉A与☉B恰好外切,且☉A与☉B是等圆,AC=2,ΔABC是等腰直角三角形,∴AB=2,x°+y°=90°,∴两个扇形(阴影部分)的面积之和=.故选B.)
10.B(解析:连接OB,OP,∵PB切☉O于点B,∴∠OBP=90°,∴PB2=OP2-OB2,而OB=2,∴PB2=OP2-4,即PB=,当OP最小时,PB最小,∵点O到直线l的距离为3,∴OP的最小值为3,∴PB的最小值为.故选B.)
11.20°(解析:∵☉O是ΔABC的外接圆,∴∠C=∠AOB,又∵∠C=70°,∴∠AOB=140°.又∵OA=OB,∴∠OAB=∠OBA,∴∠OAB=(180°-140°)÷2=20°.故填20°.)
12.2(解析:∵AC,AB为☉O的切线,且C,P分别为切点,∴AC=AP,∵AB,BD为☉O的切线,且P,D分别为切点,∴BP=BD,∴BD=PB=AB-AP=5-3=2.故填2.)
13.2(解析:如图所示,连接AO并延长,交CD于点E,连接OC,∵AB是圆O的切线,∴OA⊥AB,∵CD∥AB,∴∠AEC=90°,∴CE=CD=2,在RtΔOCE中,由勾股定理得OE=,∴AE=4,在RtΔACE中,由勾股定理得AC==2.故填2.)
14.2(解析:连接OA,由切线性质知OA⊥PA.在RtΔOAP中,∠APO=30°,∴OP=2OA,设OA=x,则OP=2x,根据勾股定理可得x2+(2)2=(2x)2,解得x=2或x=-2(舍去).故填2.)
15.48π(解析:所需纸板的面积=×12π×8=48π(cm2).故填48π.)
16.π-2(解析:S扇形==π,SΔAOB=×2×2=2,则S阴影=S扇形-SΔAOB=π-2.故填π-2.)
17.(1)解:ΔAOC是等边三角形.理由如下:∵,∴∠AOC=∠COD=60°.∵OA=OC,∴ΔAOC是等边三角形.　(2)证明:∵,∴OC⊥AD,又∵AB是☉O的直径,∴∠ADB=90°,即BD⊥AD,∴OC∥BD.
18.解:如图所示,过O作OF⊥CD,交CD于点F,连接OD,由题意知F为CD的中点,∴CF=DF,∵AE=2,EB=6,∴AB=AE+EB=2+6=8,∴OA=4,∴OE=OA-AE=4-2=2,在RtΔOEF中,∠DEB=30°,∴OF=OE=1,在RtΔODF中,OF=1,OD=4,根据勾股定理得DF=,则CD=2DF=2.
19.(1)证明:如图所示,连接OA.∵AB=AC,∠ABC=30°,∴∠ABC=∠ACB=30°,∴∠AOB=2∠ACB=60°,∴在ΔABO中,∠BAO=180°-∠ABO-∠AOB=90°,即AB⊥OA,又∵OA是☉O的半径,∴AB为☉O的切线.　(2)解:如图所示,连接AD.∵CD是☉O的直径,∴∠DAC=90°.由(1)知∠ACB=30°,∴AD=CD=4,则根据勾股定理知AC==4,即弦AC的长是4.　(3)解:由(2)知,在ΔADC中,∠DAC=90°,AD=4,AC=4,则SΔADC=AD·AC=×4×4=8.∵点O是RtΔADC斜边上的中点,∴SΔAOC=SΔADC=4.根据图示知S阴影=S扇形OAD+SΔAOC=+4+4,即图中阴影部分的面积是+4.
20.(1)解:∵AB是直径,∴∠AEB=90°,又∵∠BAC=45°,∴∠ABE=45°,∵AB=AC,∴∠ABC=∠ACB=67.5°,∴∠EBC=67.5°-45°=22.5°.　(2)证明:如图所示,连接AD,∵AB=AC,AB是直径,∴∠ADB=90°,∴BD=CD.
21.解:如图所示,过点P作PD⊥MN于D,连接PQ,则PD∥OQ,OD∥PQ,∴四边形OQPD为平行四边形,∴OQ=PD,PQ=OD.∵☉P与x轴相切于点Q,与y轴交于M(0,2),N(0,8)两点,∴OM=2,NO=8,∴NM=6,∵PD⊥NM,∴DM=3,∴OD=3+2=5,连接MQ,NQ,易证得ΔMQO∽ΔQNO,∴,∴OQ2=OM·ON=2×8=16,∴OQ=4,∴PD=4,PQ=OD=5,即点P的坐标是(4,5).
22.(1)解:①BA⊥EF;②∠CAE=∠B.答案不唯一.　(2)证明:连接AO并延长,交☉O于点D,连接CD,则AD为☉O的直径,∴∠D+∠DAC=90°,∵∠D与∠B同对弧AC,∴∠D=∠B,又∵∠CAE=∠B,∴∠D=∠CAE,∴∠DAC+∠EAC=90°,∴EF是☉O的切线.
23.(1)证法1:连接OC,∵EF是过点C的☉O的切线,∴OC⊥EF,又AD⊥EF,∴OC∥AD,∴∠OCA=∠CAD,又∵OA=OC,∴∠OCA=∠BAC,∴∠BAC=∠CAD.证法2:连接OC,∵EF是过点C的☉O的切线,∴OC⊥EF,∴∠OCA+∠ACD=90°,∵AD⊥EF,∴∠CAD+∠ACD=90°,∴∠OCA=∠CAD,∵OA=OC,∴∠OCA=∠BAC,∴∠BAC=∠CAD.　(2)解:∵∠B=30°,∴∠AOC=60°,∵OA=AB=6,∴的长为=2π.
24.解:(1)如图所示,连接OC,∵AB=4,∴OC=2,由题意知PC为☉O的切线,∠CPO=30°,∴OP=2OC=4,根据勾股定理可得PC==2.　(2)∠CMP的大小没有变化.理由如下:∵∠CMP=∠A+∠MPA,∠A=∠COP,∠MPA=∠CPO,∴∠CMP=∠A+∠MPA=∠COP+∠CPO=(∠COP+∠CPO)=×90°=45°.∴当点P在AB的延长线上运动,∠CPA的平分线交AC于点M时,∠CMP的大小不变,始终为45°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)