第二十九章 投影与视图单元质量评估试题(含解析)
文档属性
| 名称 | 第二十九章 投影与视图单元质量评估试题(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 944.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-19 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二十九章 投影与视图本章质量评估
(时间:90分钟 满分:120分)
一、选择题(每小题3分,共30分)
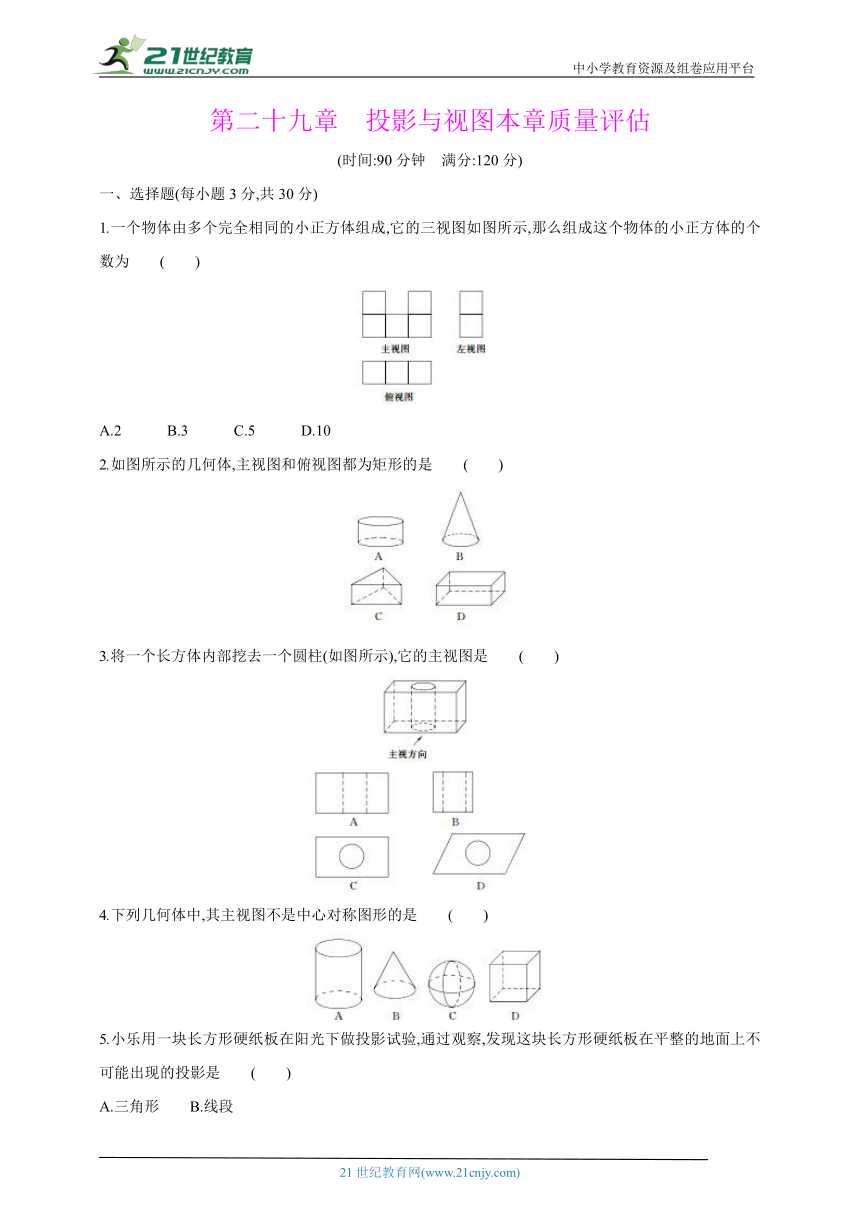
1.一个物体由多个完全相同的小正方体组成,它的三视图如图所示,那么组成这个物体的小正方体的个数为 ( )
A.2 B.3 C.5 D.10
2.如图所示的几何体,主视图和俯视图都为矩形的是 ( )
3.将一个长方体内部挖去一个圆柱(如图所示),它的主视图是 ( )
4.下列几何体中,其主视图不是中心对称图形的是 ( )
5.小乐用一块长方形硬纸板在阳光下做投影试验,通过观察,发现这块长方形硬纸板在平整的地面上不可能出现的投影是 ( )
A.三角形 B.线段
C.矩形 D.平行四边形
6.下列四个立体图形中,左视图为矩形的是 ( )
A.①③ B.①④ C.②③ D.③④
7.如图所示的是由几个小立方体所搭成的几何体的俯视图,小正方形中的数字表示在该位置上的小立方体的个数,这个几何体的主视图是 ( )
8.如图所示的是某几何体的三视图,其侧面积为 ( )
A.6 B.4π C.6π D.12π
9.用四个相同的小立方体搭几何体,要求每个几何体的主视图、左视图、俯视图中至少有两种视图的形状是相同的,下列四种摆放方式中不符合要求的是 ( )
10.如图所示的是某几何体的三视图,根据图中数据,求得该几何体的体积为 ( )
A.60π B.70π C.90π D.160π
二、填空题(每小题4分,共24分)
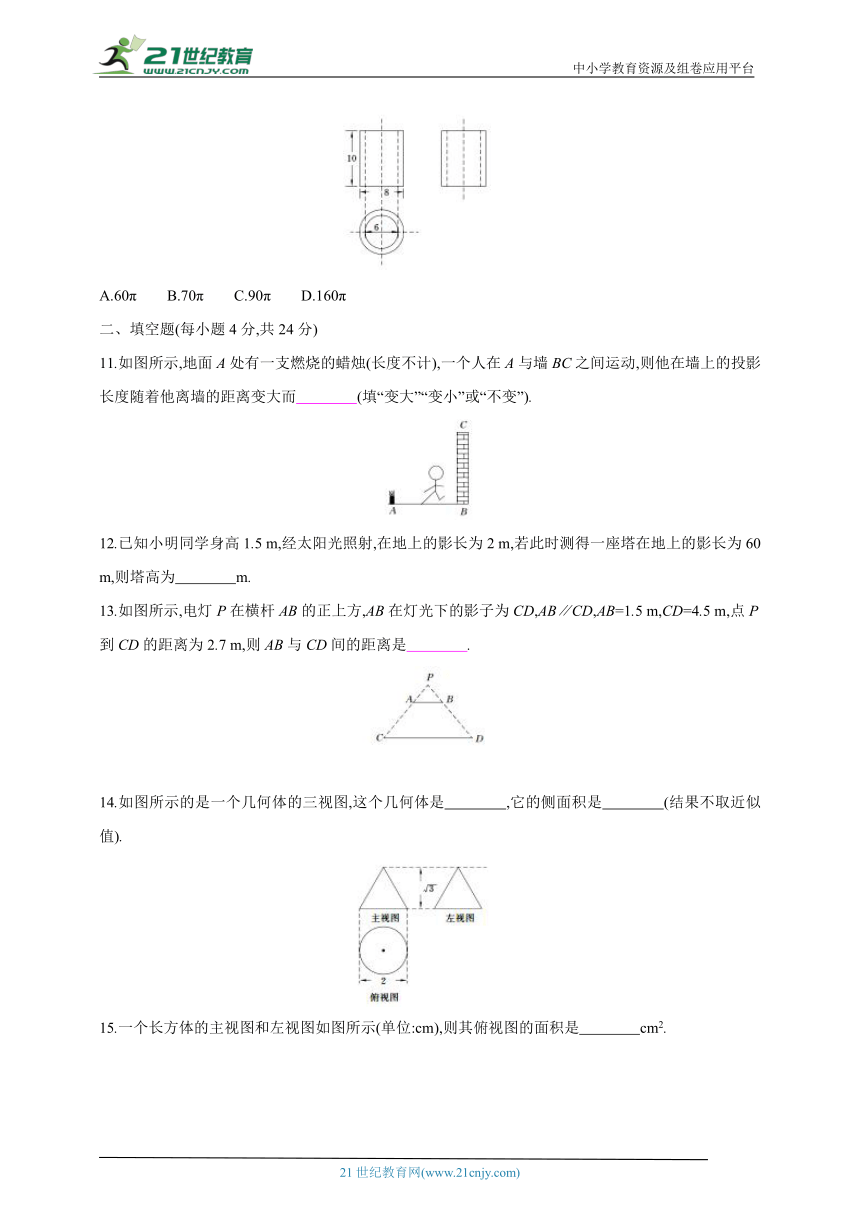
11.如图所示,地面A处有一支燃烧的蜡烛(长度不计),一个人在A与墙BC之间运动,则他在墙上的投影长度随着他离墙的距离变大而 (填“变大”“变小”或“不变”).
12.已知小明同学身高1.5 m,经太阳光照射,在地上的影长为2 m,若此时测得一座塔在地上的影长为60 m,则塔高为 m.
13.如图所示,电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=1.5 m,CD=4.5 m,点P到CD的距离为2.7 m,则AB与CD间的距离是 .
14.如图所示的是一个几何体的三视图,这个几何体是 ,它的侧面积是 (结果不取近似值).
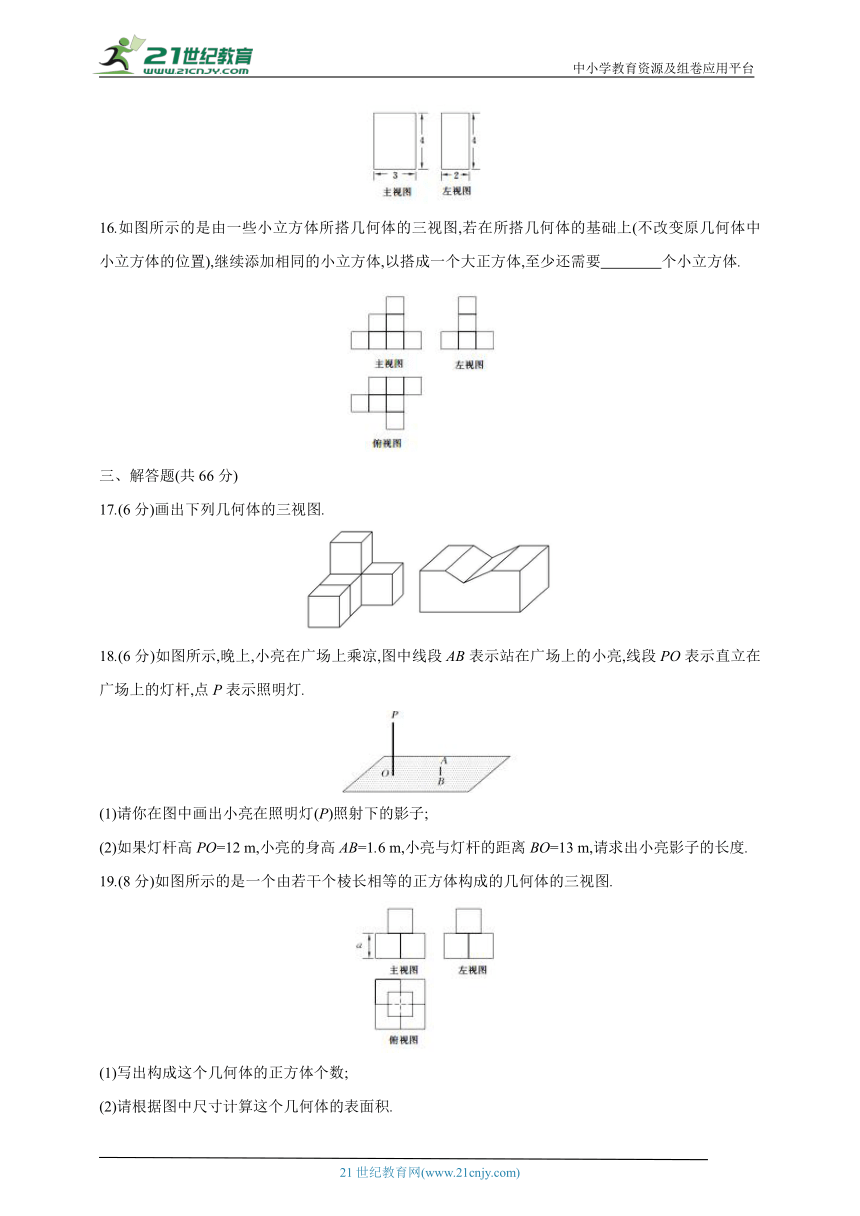
15.一个长方体的主视图和左视图如图所示(单位:cm),则其俯视图的面积是 cm2.
16.如图所示的是由一些小立方体所搭几何体的三视图,若在所搭几何体的基础上(不改变原几何体中小立方体的位置),继续添加相同的小立方体,以搭成一个大正方体,至少还需要 个小立方体.
三、解答题(共66分)
17.(6分)画出下列几何体的三视图.
18.(6分)如图所示,晚上,小亮在广场上乘凉,图中线段AB表示站在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照明灯.
(1)请你在图中画出小亮在照明灯(P)照射下的影子;
(2)如果灯杆高PO=12 m,小亮的身高AB=1.6 m,小亮与灯杆的距离BO=13 m,请求出小亮影子的长度.
19.(8分)如图所示的是一个由若干个棱长相等的正方体构成的几何体的三视图.
(1)写出构成这个几何体的正方体个数;
(2)请根据图中尺寸计算这个几何体的表面积.
20.(8分)如图所示的为某住宅区内的两幢楼,它们的高AB=CD=30 m,两楼间的距离AC=24 m,现需了解甲楼对乙楼采光的影响情况.当太阳光与水平线的夹角为30°时,求甲楼的影子在乙楼上有多高.
21.(8分)由一些大小相同的小正方体组成的几何体的主视图和俯视图如图所示.
(1)请画出这个几何体的两种左视图;
(2)若组成这个几何体的小正方体的块数为n,请你写出n的所有可能的结果.
22.(10分)学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图所示,在同一时刻,身高为1.6 m的小明(AB)的影子BC长是3 m,而小颖(EH)刚好在路灯灯泡的正下方H点,并测得HB=6 m.
(1)请在图中画出形成影子的光线,并确定路灯灯泡所在的位置G;
(2)求路灯灯泡的垂直高度GH.
23.(10分)如图所示的为某几何体的三视图(单位:cm),计算该几何体的表面积(结果保留π).
24.(10分)如图所示,王华在晚上由路灯A走向路灯B,当他走到点P时,发现身后他影子的顶部刚好接触到路灯A的底部,当他向前再步行12 m到达点Q时,发现身前他影子的顶部刚好接触路灯B的底部.已知王华的身高是1.6 m,两个路灯的高度都是9.6 m,且AP=QB=x m.
(1)求两个路灯之间的距离;
(2)当王华走到路灯B时,他在路灯A下的影长是多少
【答案与解析】
1.C(解析:从主视图与左视图可以得出此图形只有一排,一共有5个小正方体,从俯视图可以验证这一点,从而确定小正方体总数为5个.故选C.)
2.D(解析:A.圆柱主视图是矩形,俯视图是圆,故此选项错误;B.圆锥主视图是等腰三角形,俯视图是带圆心的圆,故此选项错误;C.三棱柱主视图是矩形(中间有一条虚线),俯视图是三角形,故此选项错误;D.长方体主视图和俯视图都为矩形,故此选项正确.故选D.)
3.A(解析:长方体和圆柱的主视图都是长方形,注意看不到的轮廓线用虚线表示.故选A.)
4.B(解析:A中主视图是矩形,矩形是中心对称图形,故错误;B中主视图是三角形,三角形不是中心对称图形,故正确;C中主视图是圆,圆是中心对称图形,故错误;D中主视图是正方形,正方形是中心对称图形,故错误.故选B.)
5.A(解析:长方形硬纸板与投影线平行时,形成的影子为线段;将长方形硬纸板与地面平行放置时,形成的影子为矩形;将长方形硬纸板倾斜放置形成的影子可为平行四边形;由同一时刻物高与影长成比例,且长方形对边相等,可得到投影不可能是三角形.故选A.)
6.B(解析:正方体的左视图是正方形,球的左视图是圆,圆锥的左视图是等腰三角形,圆柱的左视图是长方形,故左视图是矩形的是①④.故选B.)
7.D(解析:由俯视图可知,几个小立方体所搭成的几何体如图所示,所以主视图为D中图形.故选D.)
8.C(解析:观察三视图知该几何体为圆柱,高为3,底面直径为2,故侧面积为πdh=2π×3=6π.故选C.)
9.D(解析:A中几何体的主视图和俯视图都如图(1)所示,故A选项不合题意;B中几何体的主视图和左视图都如图(2)所示,故B选项不合题意;C中几何体的主视图和左视图都如图(3)所示,故C选项不合题意;D中几何体的主视图如图(4)所示,俯视图如图(5)所示,左视图如图(6)所示,故D选项符合题意.故选D.)
10.B(解析:观察三视图知该几何体为空心圆柱,其内圆半径为3,外圆半径为4,高为10,所以其体积为10×(42π-32π)=70π.故选B.)
11.变大(解析:连接光源和人的头顶可知,墙上的影长和人到墙的距离变化规律是距离墙越近,影长越短,距离墙越远,影长越长.则他在墙上的投影长度随着他离墙的距离变大而变大.)
12.45(解析:设塔高为x m,由同一时刻物高与影子长成比例得=,解得x=45.故填45.)
13.1.8 m(解析:∵AB∥CD,∴△PAB∽△PCD.设CD到AB的距离为x m,则=,∴=,解得x=1.8,∴AB与CD间的距离是1.8 m.)
14.圆锥 2π(解析:根据三视图可得到此几何体为圆锥,且底面圆的半径r=1,圆锥高h=,∴圆锥母线长为l=2,∴侧面积=πrl=2π.)
15.6(解析:长方体的俯视图是长是3,宽是2的长方形,它的面积=3×2=6(cm2).)
16.54(解析:由三视图易得最底层有7个小立方体,第二层有2个小立方体,第三层有1个小立方体,那么共有7+2+1=10个小立方体.若搭成一个大正方体,共需4×4×4=64个小立方体,所以还需64-10=54个小立方体.故填54.)
17.解:几何体的三视图如图所示.
18.解:(1)如图所示,连接PA并延长,交地面于点C,线段BC就是小亮在照明灯(P)照射下的影子. (2)在△CAB和△CPO中,∵∠C=∠C,∠ABC=∠POC=90°,∴△CAB∽△CPO,∴=,∴=,解得BC=2.∴小亮影子的长度为2 m.
19.解:(1)5个. (2)S表=5×6a2-10a2=20a2.即这个几何体的表面积为20a2.
20.解:过点B作BF交CD于F,过点F作FE⊥AB于点E,∵太阳光与水平线的夹角为30°,∴∠BFE=30°.∵AC=EF=24 m,∴BE=EF·tan 30°=24×=8(m),∴FC=CD-BE=(30-8)m.答:甲楼的影子在乙楼上的高度为(30-8)m.
21.解:(1)如图所示(答案不唯一). (2)n可能为8或9或10或11.
22.解:(1)如图所示,CA与HE的延长线相交于G.
(2)∵AB∥GH,∴△CBA∽△CHG,∴=.∵AB=1.6 m,BC=3 m,HB=6 m,∴=,解得GH=4.8,∴路灯灯泡的垂直高度GH为4.8 m.
23.解:这个几何体是一个简单组合体,它的下部是一个圆柱,且底面半径为6 cm,高为20 cm,它的上部是一个圆锥,且底面半径为6 cm,高为5 cm,则母线长为 cm.所以所求表面积S=π×62+2π×6×20+π×6×=276π+6π(cm2).
24.解:(1)由题意得△BQC∽△BAD,∴=,=,即=,解得x=3.∴AB=2x+12=18(m).即两个路灯之间的距离是18 m. (2)当王华走到路灯B处时(如图所示),△EAD∽△EBF,∴=,=,即=,解得BE=3.6.即王华走到路灯B时,他在路灯A下的影长是3.6 m.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第二十九章 投影与视图本章质量评估
(时间:90分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.一个物体由多个完全相同的小正方体组成,它的三视图如图所示,那么组成这个物体的小正方体的个数为 ( )
A.2 B.3 C.5 D.10
2.如图所示的几何体,主视图和俯视图都为矩形的是 ( )
3.将一个长方体内部挖去一个圆柱(如图所示),它的主视图是 ( )
4.下列几何体中,其主视图不是中心对称图形的是 ( )
5.小乐用一块长方形硬纸板在阳光下做投影试验,通过观察,发现这块长方形硬纸板在平整的地面上不可能出现的投影是 ( )
A.三角形 B.线段
C.矩形 D.平行四边形
6.下列四个立体图形中,左视图为矩形的是 ( )
A.①③ B.①④ C.②③ D.③④
7.如图所示的是由几个小立方体所搭成的几何体的俯视图,小正方形中的数字表示在该位置上的小立方体的个数,这个几何体的主视图是 ( )
8.如图所示的是某几何体的三视图,其侧面积为 ( )
A.6 B.4π C.6π D.12π
9.用四个相同的小立方体搭几何体,要求每个几何体的主视图、左视图、俯视图中至少有两种视图的形状是相同的,下列四种摆放方式中不符合要求的是 ( )
10.如图所示的是某几何体的三视图,根据图中数据,求得该几何体的体积为 ( )
A.60π B.70π C.90π D.160π
二、填空题(每小题4分,共24分)
11.如图所示,地面A处有一支燃烧的蜡烛(长度不计),一个人在A与墙BC之间运动,则他在墙上的投影长度随着他离墙的距离变大而 (填“变大”“变小”或“不变”).
12.已知小明同学身高1.5 m,经太阳光照射,在地上的影长为2 m,若此时测得一座塔在地上的影长为60 m,则塔高为 m.
13.如图所示,电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=1.5 m,CD=4.5 m,点P到CD的距离为2.7 m,则AB与CD间的距离是 .
14.如图所示的是一个几何体的三视图,这个几何体是 ,它的侧面积是 (结果不取近似值).
15.一个长方体的主视图和左视图如图所示(单位:cm),则其俯视图的面积是 cm2.
16.如图所示的是由一些小立方体所搭几何体的三视图,若在所搭几何体的基础上(不改变原几何体中小立方体的位置),继续添加相同的小立方体,以搭成一个大正方体,至少还需要 个小立方体.
三、解答题(共66分)
17.(6分)画出下列几何体的三视图.
18.(6分)如图所示,晚上,小亮在广场上乘凉,图中线段AB表示站在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照明灯.
(1)请你在图中画出小亮在照明灯(P)照射下的影子;
(2)如果灯杆高PO=12 m,小亮的身高AB=1.6 m,小亮与灯杆的距离BO=13 m,请求出小亮影子的长度.
19.(8分)如图所示的是一个由若干个棱长相等的正方体构成的几何体的三视图.
(1)写出构成这个几何体的正方体个数;
(2)请根据图中尺寸计算这个几何体的表面积.
20.(8分)如图所示的为某住宅区内的两幢楼,它们的高AB=CD=30 m,两楼间的距离AC=24 m,现需了解甲楼对乙楼采光的影响情况.当太阳光与水平线的夹角为30°时,求甲楼的影子在乙楼上有多高.
21.(8分)由一些大小相同的小正方体组成的几何体的主视图和俯视图如图所示.
(1)请画出这个几何体的两种左视图;
(2)若组成这个几何体的小正方体的块数为n,请你写出n的所有可能的结果.
22.(10分)学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图所示,在同一时刻,身高为1.6 m的小明(AB)的影子BC长是3 m,而小颖(EH)刚好在路灯灯泡的正下方H点,并测得HB=6 m.
(1)请在图中画出形成影子的光线,并确定路灯灯泡所在的位置G;
(2)求路灯灯泡的垂直高度GH.
23.(10分)如图所示的为某几何体的三视图(单位:cm),计算该几何体的表面积(结果保留π).
24.(10分)如图所示,王华在晚上由路灯A走向路灯B,当他走到点P时,发现身后他影子的顶部刚好接触到路灯A的底部,当他向前再步行12 m到达点Q时,发现身前他影子的顶部刚好接触路灯B的底部.已知王华的身高是1.6 m,两个路灯的高度都是9.6 m,且AP=QB=x m.
(1)求两个路灯之间的距离;
(2)当王华走到路灯B时,他在路灯A下的影长是多少
【答案与解析】
1.C(解析:从主视图与左视图可以得出此图形只有一排,一共有5个小正方体,从俯视图可以验证这一点,从而确定小正方体总数为5个.故选C.)
2.D(解析:A.圆柱主视图是矩形,俯视图是圆,故此选项错误;B.圆锥主视图是等腰三角形,俯视图是带圆心的圆,故此选项错误;C.三棱柱主视图是矩形(中间有一条虚线),俯视图是三角形,故此选项错误;D.长方体主视图和俯视图都为矩形,故此选项正确.故选D.)
3.A(解析:长方体和圆柱的主视图都是长方形,注意看不到的轮廓线用虚线表示.故选A.)
4.B(解析:A中主视图是矩形,矩形是中心对称图形,故错误;B中主视图是三角形,三角形不是中心对称图形,故正确;C中主视图是圆,圆是中心对称图形,故错误;D中主视图是正方形,正方形是中心对称图形,故错误.故选B.)
5.A(解析:长方形硬纸板与投影线平行时,形成的影子为线段;将长方形硬纸板与地面平行放置时,形成的影子为矩形;将长方形硬纸板倾斜放置形成的影子可为平行四边形;由同一时刻物高与影长成比例,且长方形对边相等,可得到投影不可能是三角形.故选A.)
6.B(解析:正方体的左视图是正方形,球的左视图是圆,圆锥的左视图是等腰三角形,圆柱的左视图是长方形,故左视图是矩形的是①④.故选B.)
7.D(解析:由俯视图可知,几个小立方体所搭成的几何体如图所示,所以主视图为D中图形.故选D.)
8.C(解析:观察三视图知该几何体为圆柱,高为3,底面直径为2,故侧面积为πdh=2π×3=6π.故选C.)
9.D(解析:A中几何体的主视图和俯视图都如图(1)所示,故A选项不合题意;B中几何体的主视图和左视图都如图(2)所示,故B选项不合题意;C中几何体的主视图和左视图都如图(3)所示,故C选项不合题意;D中几何体的主视图如图(4)所示,俯视图如图(5)所示,左视图如图(6)所示,故D选项符合题意.故选D.)
10.B(解析:观察三视图知该几何体为空心圆柱,其内圆半径为3,外圆半径为4,高为10,所以其体积为10×(42π-32π)=70π.故选B.)
11.变大(解析:连接光源和人的头顶可知,墙上的影长和人到墙的距离变化规律是距离墙越近,影长越短,距离墙越远,影长越长.则他在墙上的投影长度随着他离墙的距离变大而变大.)
12.45(解析:设塔高为x m,由同一时刻物高与影子长成比例得=,解得x=45.故填45.)
13.1.8 m(解析:∵AB∥CD,∴△PAB∽△PCD.设CD到AB的距离为x m,则=,∴=,解得x=1.8,∴AB与CD间的距离是1.8 m.)
14.圆锥 2π(解析:根据三视图可得到此几何体为圆锥,且底面圆的半径r=1,圆锥高h=,∴圆锥母线长为l=2,∴侧面积=πrl=2π.)
15.6(解析:长方体的俯视图是长是3,宽是2的长方形,它的面积=3×2=6(cm2).)
16.54(解析:由三视图易得最底层有7个小立方体,第二层有2个小立方体,第三层有1个小立方体,那么共有7+2+1=10个小立方体.若搭成一个大正方体,共需4×4×4=64个小立方体,所以还需64-10=54个小立方体.故填54.)
17.解:几何体的三视图如图所示.
18.解:(1)如图所示,连接PA并延长,交地面于点C,线段BC就是小亮在照明灯(P)照射下的影子. (2)在△CAB和△CPO中,∵∠C=∠C,∠ABC=∠POC=90°,∴△CAB∽△CPO,∴=,∴=,解得BC=2.∴小亮影子的长度为2 m.
19.解:(1)5个. (2)S表=5×6a2-10a2=20a2.即这个几何体的表面积为20a2.
20.解:过点B作BF交CD于F,过点F作FE⊥AB于点E,∵太阳光与水平线的夹角为30°,∴∠BFE=30°.∵AC=EF=24 m,∴BE=EF·tan 30°=24×=8(m),∴FC=CD-BE=(30-8)m.答:甲楼的影子在乙楼上的高度为(30-8)m.
21.解:(1)如图所示(答案不唯一). (2)n可能为8或9或10或11.
22.解:(1)如图所示,CA与HE的延长线相交于G.
(2)∵AB∥GH,∴△CBA∽△CHG,∴=.∵AB=1.6 m,BC=3 m,HB=6 m,∴=,解得GH=4.8,∴路灯灯泡的垂直高度GH为4.8 m.
23.解:这个几何体是一个简单组合体,它的下部是一个圆柱,且底面半径为6 cm,高为20 cm,它的上部是一个圆锥,且底面半径为6 cm,高为5 cm,则母线长为 cm.所以所求表面积S=π×62+2π×6×20+π×6×=276π+6π(cm2).
24.解:(1)由题意得△BQC∽△BAD,∴=,=,即=,解得x=3.∴AB=2x+12=18(m).即两个路灯之间的距离是18 m. (2)当王华走到路灯B处时(如图所示),△EAD∽△EBF,∴=,=,即=,解得BE=3.6.即王华走到路灯B时,他在路灯A下的影长是3.6 m.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
