第二十七章 相似单元质量评估试题(含解析)
文档属性
| 名称 | 第二十七章 相似单元质量评估试题(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-19 16:35:03 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二十七章 相似本章质量评估
(时间:90分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.下列四条线段中,不是成比例线段的是 ( )
A.a=3,b=6,c=2,d=4
B.a=,b=8,c=5,d=15
C.a=1,b=,c=,d=
D.a=,b=1,c=,d=
2.△ABC∽△A'B'C',∠A=45°,∠B=100°,则∠C'等于 ( )
A.45° B.100°
C.55° D.35°
3.△ABC与△A'B'C'是位似图形,且△ABC与△A'B'C'的相似比是1∶2,已知△ABC的面积是3,则△A'B'C'的面积是 ( )
A.3 B.6 C.9 D.12
4.如图所示,l1∥l2∥l3, 直线a,b与l1,l2,l3分别相交于点A,B,C和点D,E,F,若=,DE=4,则EF的长是 ( )
A. B. C.6 D.10
5.如图所示,在 ABCD中,E为CD上一点,连接AE,BD,且AE,BD交于点F,S△DEF∶S△ABF=4∶25,则DE∶EC等于 ( )
A.2∶5 B.2∶3 C.3∶5 D.3∶2
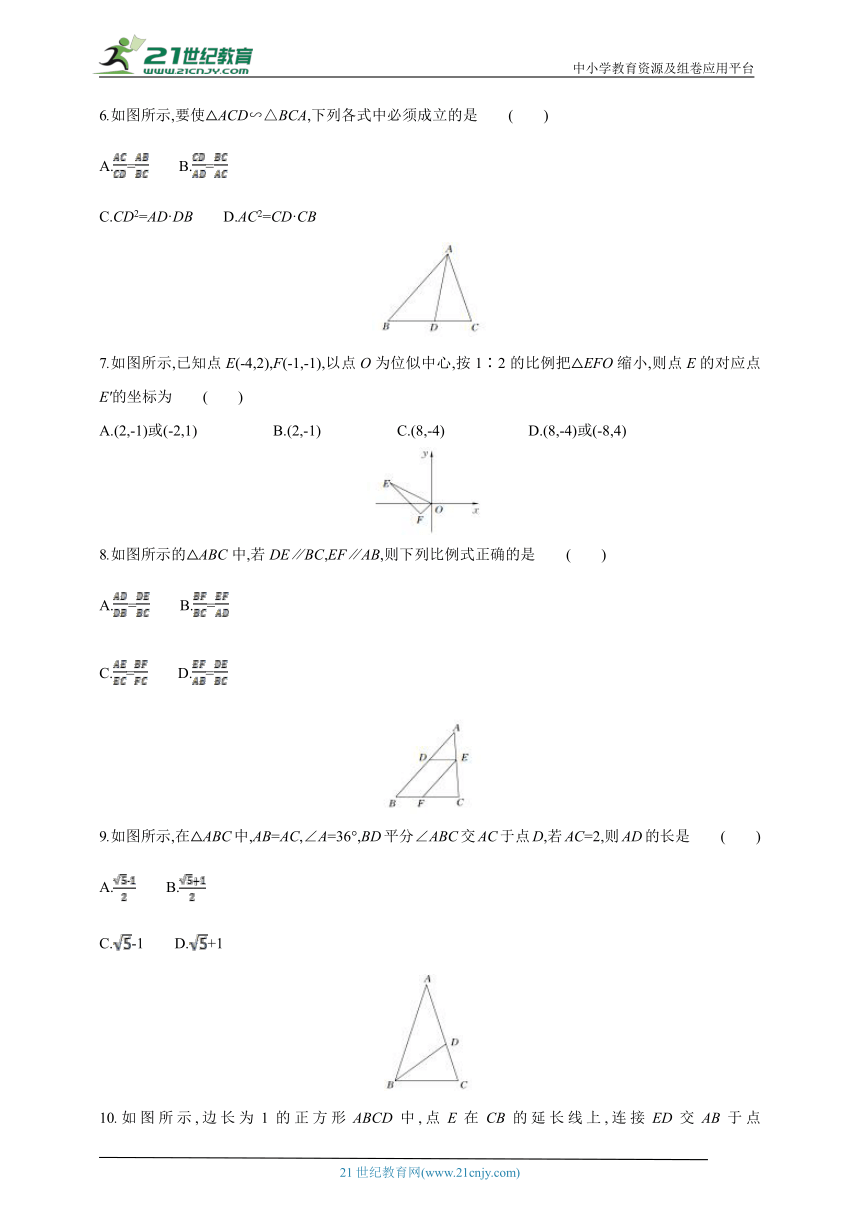
6.如图所示,要使△ACD∽△BCA,下列各式中必须成立的是 ( )
A.= B.=
C.CD2=AD·DB D.AC2=CD·CB
7.如图所示,已知点E(-4,2),F(-1,-1),以点O为位似中心,按1∶2的比例把△EFO缩小,则点E的对应点E'的坐标为 ( )
A.(2,-1)或(-2,1) B.(2,-1) C.(8,-4) D.(8,-4)或(-8,4)
8.如图所示的△ABC中,若DE∥BC,EF∥AB,则下列比例式正确的是 ( )
A.= B.=
C.= D.=
9.如图所示,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,若AC=2,则AD的长是 ( )
A. B.
C.-1 D.+1
10.如图所示,边长为1的正方形ABCD中,点E在CB的延长线上,连接ED交AB于点F,AF=x(0.2≤x≤0.8),EC=y.则在下面的函数图象中,大致能表示y与x之间函数关系的是 ( )
二、填空题(每小题4分,共24分)
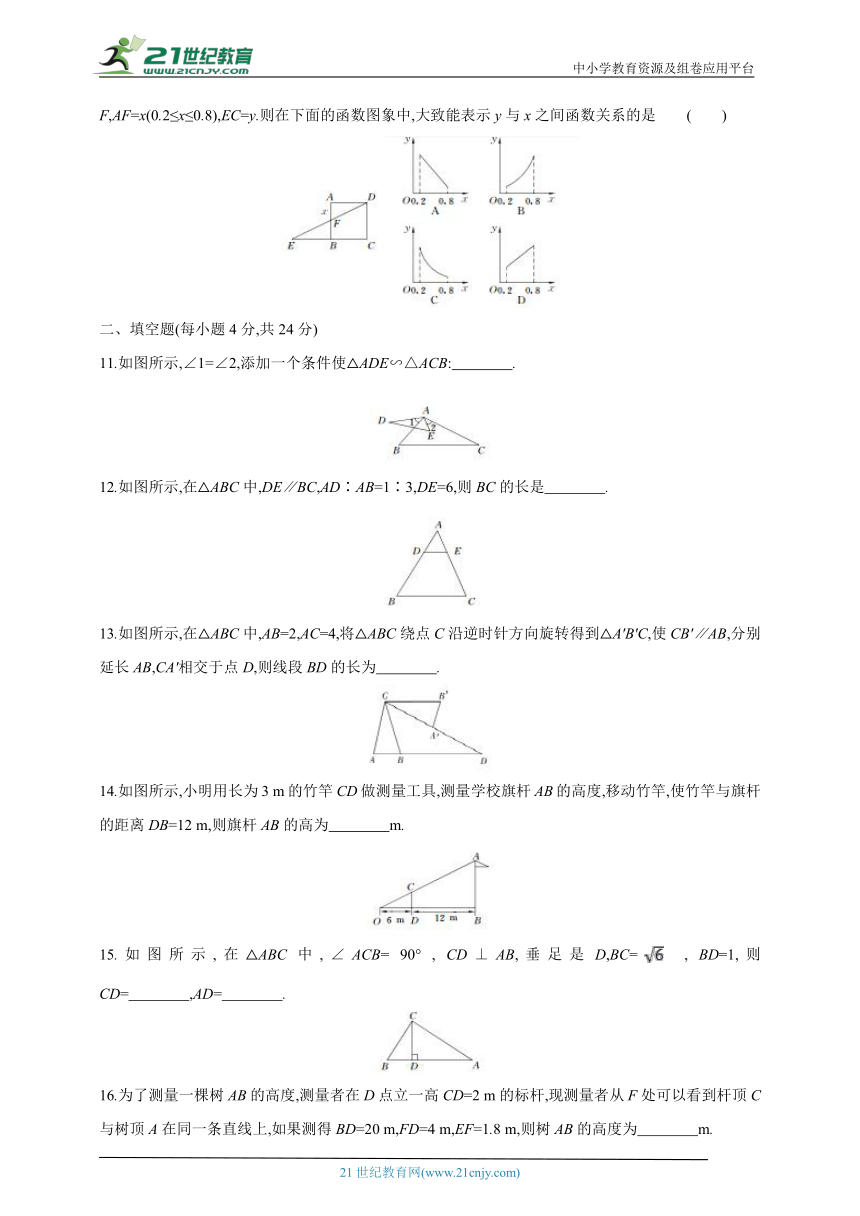
11.如图所示,∠1=∠2,添加一个条件使△ADE∽△ACB: .
12.如图所示,在△ABC中,DE∥BC,AD∶AB=1∶3,DE=6,则BC的长是 .
13.如图所示,在△ABC中,AB=2,AC=4,将△ABC绕点C沿逆时针方向旋转得到△A'B'C,使CB'∥AB,分别延长AB,CA'相交于点D,则线段BD的长为 .
14.如图所示,小明用长为3 m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12 m,则旗杆AB的高为 m.
15.如图所示,在△ABC中,∠ACB= 90° , CD⊥AB,垂足是D,BC= , BD=1,则CD= ,AD= .
16.为了测量一棵树AB的高度,测量者在D点立一高CD=2 m的标杆,现测量者从F处可以看到杆顶C与树顶A在同一条直线上,如果测得BD=20 m,FD=4 m,EF=1.8 m,则树AB的高度为 m.
三、解答题(共66分)
17.(5分)如图所示,已知在△ABC与△DEF中,∠C=54°,∠A=47°,∠F=54°,∠E=79°.求证△ABC∽△DEF.
18.(6分)如图所示,在边长为9的正三角形ABC中,BD=3,∠ADE=60°,求AE的长.
19.(8分)如图所示,点C,D在线段AB上,△PCD是等边三角形.
(1)当AC,CD,DB满足怎样的关系时,△ACP∽△PDB
(2)当△ACP∽△PDB时,求∠APB的度数.
20.(8分)如图所示,在边长均为1的小正方形网格纸中,△OAB的顶点O,A,B均在格点上,且O是直角坐标系的原点,点A在x轴上.
(1)以O为位似中心,将△OAB放大,使得放大后的△OA1B1与△OAB对应线段的比为2∶1,画出△OA1B1(所画△OA1B1与△OAB在原点两侧);
(2)求出线段A1B1所在直线的函数关系式.
21.(8分)如图所示,直线PM切☉O于点M,直线PO交☉O于A,B两点,弦AC∥PM,连接OM,BC.求证:
(1)△ABC∽△POM;
(2)2OA2=OP·BC.
22.(9分)如图所示,在Rt△ABC中,∠ACB=90°,以AC为直径的☉O与AB边交于点D,过点D作☉O的切线,交BC于点E.
(1)求证点E是边BC的中点;
(2)若EC=3,BD=2,求☉O的直径AC的长度;
(3)若以点O,D,E,C为顶点的四边形是正方形,试判断△ABC的形状,并说明理由.
23.(10分)如图所示,在直角梯形OABC中,BC∥AO,∠AOC=90°,点A,B的坐标分别为(5,0),(2,6),点D为AB上一点,且BD=2AD.双曲线y=(x>0)经过点D,交BC于点E.
(1)求双曲线的解析式;
(2)求四边形ODBE的面积.
24.(12分)如图所示,在△ABC中,BA=BC=20 cm,AC=30 cm,点P从点A出发,沿AB以每秒4 cm的速度向点B运动,同时点Q从C点出发,沿CA以每秒3 cm的速度向点A运动,设运动时间为x秒.
(1)当x为何值时,BP=CQ
(2)当x为何值时,PQ∥BC
(3)△APQ能否与△CQB相似 若能,求出x的值;若不能,请说明理由.
【答案与解析】
1.C(解析:A选项中,满足=,是成比例线段;B选项中,满足=;D选项中,满足=.故选C.)
2.D(解析:△ABC∽△A'B'C',则∠A=∠A'=45°,∠B=∠B'=100°,根据三角形的内角和定理得到∠C'=180°-∠A'-∠B'=180°-45°-100°=35°.故选D.)
3.D(解析:∵△ABC与△A'B'C'是位似图形,且△ABC与△A'B'C'的相似比是1∶2,△ABC的面积是3,∴△ABC与△A'B'C'的面积比为1∶4,则△A'B'C'的面积是12.故选D.)
4.C(解析:∵l1∥l2∥l3,∴=,∵=,DE=4,∴EF=6.故选C.)
5.B(解析:∵四边形ABCD是平行四边形,∴AB∥CD,∴∠FAB=∠DEF,又∠AFB=∠EFD,∴△DEF∽△BAF,∵S△DEF∶S△ABF=4∶25,∴DE∶AB=2∶5,∵AB=CD,∴DE∶EC=2∶3.故选B.)
6.D(解析:∵∠C=∠C,∴要使△ACD∽△BCA,则两边必须满足=,即AC2=CD·CB.故选D.)
7.A(解析:根据题意可知点E的对应点E'的坐标是E(-4,2)的坐标同时乘或,所以点E'的坐标为(-2,1)或(2,-1).故选A.)
8.C(解析:∵DE∥BC,EF∥AB,∴四边形DEFB是平行四边形,∴DE=BF,BD=EF.∵DE∥BC,∴==,∵EF∥AB,∴==,∵EF∥AB,∴=.故选C.)
9.C(解析:由题知∠A=∠DBC=36°,∠C为公共角,∴△ABC∽△BDC, 且AD=BD=BC. 设BD=x,则BC=x,CD=2-x.∵=,∴=. 整理得x2+2x-4=0, 解方程得x=-1±, ∵x为正数, ∴x=-1+.故选C.)
10.C(解析:根据题意知BF=1-x,BE=y-1,且△EFB∽△EDC,则=,即=,所以y=(0.2≤x≤0.8),该函数图象是位于第一象限的双曲线的一部分.A,D的图象都是直线的一部分,B的图象是抛物线的一部分,C的图象是双曲线的一部分.故选C.)
11.∠B=∠E(答案不唯一)
12.18(解析:∵DE∥BC,∴△ADE∽△ABC,∴=,∵AD∶AB=1∶3,DE=6,∴BC=3×6=18.故填18.)
13.6(解析:∵将△ABC绕点C沿逆时针方向旋转得到△A'B'C,∴AC=CA'=4,AB=B'A'=2,∠A=∠CA'B',∵CB'∥AB,∴∠B'CA'=∠D,∴△CAD∽△B'A'C,∴=,∴=,解得AD=8,∴BD=AD-AB=8-2=6.故填6.)
14.9(解析:由题意得CD∥AB,∴△OCD∽△OAB,∴=,即=,解得AB=9(m).故填9.)
15. 5(解析:在Rt△DBC中,由勾股定理得CD==,由题意知△DBC∽△DCA,可得=,即=,因此AD=5.)
16.3(解析:如图所示,过E作EH⊥AB于H,交CD于G,则CG=CD-EF=0.2 m,EG=FD=4 m,EH=BF=BD+DF=24 m.易知△CEG∽△AEH,则有=,即=,∴AH=1.2(m),∴AB=AH+BH=AH+EF=3 m,即树的高度为3 m.故填3.)
17.证明:在△ABC中,∠B=180°-∠A-∠C=79°,在△ABC和△DEF中,∠B=∠E,∠C=∠F,∴△ABC∽△DEF.
18.解:∵△ABC是等边三角形,∴∠B=∠C=60°,AB=BC.∴CD=BC-BD=9-3=6,∴∠BAD+∠ADB=120°.∵∠ADE=60°,∴∠ADB+∠EDC=120°,∴∠DAB=∠EDC,又∵∠B=∠C=60°,∴△ABD∽△DCE,则=,即=,解得CE=2,∴AE=AC-CE=9-2=7.
19.解:(1)当CD2=AC·DB时,△ACP∽△PDB.∵△PCD是等边三角形,∴∠PCD=∠PDC=60°,∴∠ACP=∠PDB=120°,若CD2=AC·DB,由PC=PD=CD可得PC·PD=AC·DB,即=,∴△ACP∽△PDB. (2)当△ACP∽△PDB时,∠APC=∠PBD,由题知∠PDC=60°,∴∠DPB+∠DBP=60°,∴∠APC+∠BPD=60°,∴∠APB=∠CPD+∠APC+∠BPD=120°,即∠APB的度数为120°.
20.解:(1)如图所示的△OA1B1就是△OAB放大后的图象.
(2)由(1)可得点A1,B1的坐标分别为(4,0),(2,-4),故设此直线的解析式为y=kx+b(k≠0),∴解得故线段A1B1所在直线的函数关系式为y=2x-8.
21.证明:(1)∵直线PM切☉O于点M,∴∠PMO=90°,∵弦AB是直径,∴∠ACB=90°,∴∠ACB=∠PMO,∵AC∥PM,∴∠CAB=∠P,∴△ABC∽△POM. (2)∵△ABC∽△POM,∴=,又AB=2OA,OA=OM,∴=,∴2OA2=OP·BC.
22.(1)证明:连接DO ,∵∠ACB=90°,AC为直径, ∴EC为☉O的切线,又∵ED也为☉O的切线, ∴EC=ED.又∵∠EDO=90°,∴∠BDE+∠ADO=90°,∴∠BDE+∠A=90°,又∵∠B+∠A=90°,∴∠BDE=∠B,∴EB=ED.∴EB=EC,即点E是边BC的中点. (2)解:∵BC,BA分别是☉O的切线和割线,∴BC2=BD·BA , ∴(2EC)2= BD·BA ,即36=2·BA,∴BA=3,在Rt△ABC中,由勾股定理得 AC===3. (3)解:△ABC是等腰直角三角形.理由如下:∵四边形ODEC为正方形,∴∠DOC=∠ACB=90°,即DO∥BC,又∵点E是边BC的中点, ∴BC=2OD=AC,∴△ABC是等腰直角三角形.
23.解:(1)过点B,D作x轴的垂线,垂足分别为点M,N.∵A(5,0),B(2,6),∴OM=BC=2,BM=OC=6,AM=3.∵DN∥BM,∴△AND∽△AMB,∴===,∴DN =2,AN=1, ∴ON=4.∴点D的坐标为(4,2).
∵双曲线y=(x>0)经过点D,∴k=2×4=8.∴双曲线的解析式为y=. (2)∵点E在BC上,∴点E的纵坐标为6.又∵点E在双曲线y=上,∴点E的坐标为,∴CE=.∴S四边形ODBE=S梯形OABC-S△OCE-S△AOD =×(BC+OA)×OC-×OC×CE-×OA×DN =×(2+5)×6-×6×-×5×2=12.∴四边形ODBE的面积为12.
24.解:(1)依题意可得BP=20-4x,CQ=3x.当BP=CQ时,20-4x=3x,∴x=.当x=时,BP=CQ. (2)由题知AP=4x,AB=20,AQ=30-3x,AC=30.所以当PQ∥BC时,有=,即=.解得x=.当x=时,PQ∥BC. (3)能.①当△APQ∽△CQB时,有=,即=,解得x=.②当△APQ∽△CBQ时,有=,即=.解得x=5或x=-10(舍去).综上,当x=或x=5时,△APQ与△CQB相似.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第二十七章 相似本章质量评估
(时间:90分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.下列四条线段中,不是成比例线段的是 ( )
A.a=3,b=6,c=2,d=4
B.a=,b=8,c=5,d=15
C.a=1,b=,c=,d=
D.a=,b=1,c=,d=
2.△ABC∽△A'B'C',∠A=45°,∠B=100°,则∠C'等于 ( )
A.45° B.100°
C.55° D.35°
3.△ABC与△A'B'C'是位似图形,且△ABC与△A'B'C'的相似比是1∶2,已知△ABC的面积是3,则△A'B'C'的面积是 ( )
A.3 B.6 C.9 D.12
4.如图所示,l1∥l2∥l3, 直线a,b与l1,l2,l3分别相交于点A,B,C和点D,E,F,若=,DE=4,则EF的长是 ( )
A. B. C.6 D.10
5.如图所示,在 ABCD中,E为CD上一点,连接AE,BD,且AE,BD交于点F,S△DEF∶S△ABF=4∶25,则DE∶EC等于 ( )
A.2∶5 B.2∶3 C.3∶5 D.3∶2
6.如图所示,要使△ACD∽△BCA,下列各式中必须成立的是 ( )
A.= B.=
C.CD2=AD·DB D.AC2=CD·CB
7.如图所示,已知点E(-4,2),F(-1,-1),以点O为位似中心,按1∶2的比例把△EFO缩小,则点E的对应点E'的坐标为 ( )
A.(2,-1)或(-2,1) B.(2,-1) C.(8,-4) D.(8,-4)或(-8,4)
8.如图所示的△ABC中,若DE∥BC,EF∥AB,则下列比例式正确的是 ( )
A.= B.=
C.= D.=
9.如图所示,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,若AC=2,则AD的长是 ( )
A. B.
C.-1 D.+1
10.如图所示,边长为1的正方形ABCD中,点E在CB的延长线上,连接ED交AB于点F,AF=x(0.2≤x≤0.8),EC=y.则在下面的函数图象中,大致能表示y与x之间函数关系的是 ( )
二、填空题(每小题4分,共24分)
11.如图所示,∠1=∠2,添加一个条件使△ADE∽△ACB: .
12.如图所示,在△ABC中,DE∥BC,AD∶AB=1∶3,DE=6,则BC的长是 .
13.如图所示,在△ABC中,AB=2,AC=4,将△ABC绕点C沿逆时针方向旋转得到△A'B'C,使CB'∥AB,分别延长AB,CA'相交于点D,则线段BD的长为 .
14.如图所示,小明用长为3 m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12 m,则旗杆AB的高为 m.
15.如图所示,在△ABC中,∠ACB= 90° , CD⊥AB,垂足是D,BC= , BD=1,则CD= ,AD= .
16.为了测量一棵树AB的高度,测量者在D点立一高CD=2 m的标杆,现测量者从F处可以看到杆顶C与树顶A在同一条直线上,如果测得BD=20 m,FD=4 m,EF=1.8 m,则树AB的高度为 m.
三、解答题(共66分)
17.(5分)如图所示,已知在△ABC与△DEF中,∠C=54°,∠A=47°,∠F=54°,∠E=79°.求证△ABC∽△DEF.
18.(6分)如图所示,在边长为9的正三角形ABC中,BD=3,∠ADE=60°,求AE的长.
19.(8分)如图所示,点C,D在线段AB上,△PCD是等边三角形.
(1)当AC,CD,DB满足怎样的关系时,△ACP∽△PDB
(2)当△ACP∽△PDB时,求∠APB的度数.
20.(8分)如图所示,在边长均为1的小正方形网格纸中,△OAB的顶点O,A,B均在格点上,且O是直角坐标系的原点,点A在x轴上.
(1)以O为位似中心,将△OAB放大,使得放大后的△OA1B1与△OAB对应线段的比为2∶1,画出△OA1B1(所画△OA1B1与△OAB在原点两侧);
(2)求出线段A1B1所在直线的函数关系式.
21.(8分)如图所示,直线PM切☉O于点M,直线PO交☉O于A,B两点,弦AC∥PM,连接OM,BC.求证:
(1)△ABC∽△POM;
(2)2OA2=OP·BC.
22.(9分)如图所示,在Rt△ABC中,∠ACB=90°,以AC为直径的☉O与AB边交于点D,过点D作☉O的切线,交BC于点E.
(1)求证点E是边BC的中点;
(2)若EC=3,BD=2,求☉O的直径AC的长度;
(3)若以点O,D,E,C为顶点的四边形是正方形,试判断△ABC的形状,并说明理由.
23.(10分)如图所示,在直角梯形OABC中,BC∥AO,∠AOC=90°,点A,B的坐标分别为(5,0),(2,6),点D为AB上一点,且BD=2AD.双曲线y=(x>0)经过点D,交BC于点E.
(1)求双曲线的解析式;
(2)求四边形ODBE的面积.
24.(12分)如图所示,在△ABC中,BA=BC=20 cm,AC=30 cm,点P从点A出发,沿AB以每秒4 cm的速度向点B运动,同时点Q从C点出发,沿CA以每秒3 cm的速度向点A运动,设运动时间为x秒.
(1)当x为何值时,BP=CQ
(2)当x为何值时,PQ∥BC
(3)△APQ能否与△CQB相似 若能,求出x的值;若不能,请说明理由.
【答案与解析】
1.C(解析:A选项中,满足=,是成比例线段;B选项中,满足=;D选项中,满足=.故选C.)
2.D(解析:△ABC∽△A'B'C',则∠A=∠A'=45°,∠B=∠B'=100°,根据三角形的内角和定理得到∠C'=180°-∠A'-∠B'=180°-45°-100°=35°.故选D.)
3.D(解析:∵△ABC与△A'B'C'是位似图形,且△ABC与△A'B'C'的相似比是1∶2,△ABC的面积是3,∴△ABC与△A'B'C'的面积比为1∶4,则△A'B'C'的面积是12.故选D.)
4.C(解析:∵l1∥l2∥l3,∴=,∵=,DE=4,∴EF=6.故选C.)
5.B(解析:∵四边形ABCD是平行四边形,∴AB∥CD,∴∠FAB=∠DEF,又∠AFB=∠EFD,∴△DEF∽△BAF,∵S△DEF∶S△ABF=4∶25,∴DE∶AB=2∶5,∵AB=CD,∴DE∶EC=2∶3.故选B.)
6.D(解析:∵∠C=∠C,∴要使△ACD∽△BCA,则两边必须满足=,即AC2=CD·CB.故选D.)
7.A(解析:根据题意可知点E的对应点E'的坐标是E(-4,2)的坐标同时乘或,所以点E'的坐标为(-2,1)或(2,-1).故选A.)
8.C(解析:∵DE∥BC,EF∥AB,∴四边形DEFB是平行四边形,∴DE=BF,BD=EF.∵DE∥BC,∴==,∵EF∥AB,∴==,∵EF∥AB,∴=.故选C.)
9.C(解析:由题知∠A=∠DBC=36°,∠C为公共角,∴△ABC∽△BDC, 且AD=BD=BC. 设BD=x,则BC=x,CD=2-x.∵=,∴=. 整理得x2+2x-4=0, 解方程得x=-1±, ∵x为正数, ∴x=-1+.故选C.)
10.C(解析:根据题意知BF=1-x,BE=y-1,且△EFB∽△EDC,则=,即=,所以y=(0.2≤x≤0.8),该函数图象是位于第一象限的双曲线的一部分.A,D的图象都是直线的一部分,B的图象是抛物线的一部分,C的图象是双曲线的一部分.故选C.)
11.∠B=∠E(答案不唯一)
12.18(解析:∵DE∥BC,∴△ADE∽△ABC,∴=,∵AD∶AB=1∶3,DE=6,∴BC=3×6=18.故填18.)
13.6(解析:∵将△ABC绕点C沿逆时针方向旋转得到△A'B'C,∴AC=CA'=4,AB=B'A'=2,∠A=∠CA'B',∵CB'∥AB,∴∠B'CA'=∠D,∴△CAD∽△B'A'C,∴=,∴=,解得AD=8,∴BD=AD-AB=8-2=6.故填6.)
14.9(解析:由题意得CD∥AB,∴△OCD∽△OAB,∴=,即=,解得AB=9(m).故填9.)
15. 5(解析:在Rt△DBC中,由勾股定理得CD==,由题意知△DBC∽△DCA,可得=,即=,因此AD=5.)
16.3(解析:如图所示,过E作EH⊥AB于H,交CD于G,则CG=CD-EF=0.2 m,EG=FD=4 m,EH=BF=BD+DF=24 m.易知△CEG∽△AEH,则有=,即=,∴AH=1.2(m),∴AB=AH+BH=AH+EF=3 m,即树的高度为3 m.故填3.)
17.证明:在△ABC中,∠B=180°-∠A-∠C=79°,在△ABC和△DEF中,∠B=∠E,∠C=∠F,∴△ABC∽△DEF.
18.解:∵△ABC是等边三角形,∴∠B=∠C=60°,AB=BC.∴CD=BC-BD=9-3=6,∴∠BAD+∠ADB=120°.∵∠ADE=60°,∴∠ADB+∠EDC=120°,∴∠DAB=∠EDC,又∵∠B=∠C=60°,∴△ABD∽△DCE,则=,即=,解得CE=2,∴AE=AC-CE=9-2=7.
19.解:(1)当CD2=AC·DB时,△ACP∽△PDB.∵△PCD是等边三角形,∴∠PCD=∠PDC=60°,∴∠ACP=∠PDB=120°,若CD2=AC·DB,由PC=PD=CD可得PC·PD=AC·DB,即=,∴△ACP∽△PDB. (2)当△ACP∽△PDB时,∠APC=∠PBD,由题知∠PDC=60°,∴∠DPB+∠DBP=60°,∴∠APC+∠BPD=60°,∴∠APB=∠CPD+∠APC+∠BPD=120°,即∠APB的度数为120°.
20.解:(1)如图所示的△OA1B1就是△OAB放大后的图象.
(2)由(1)可得点A1,B1的坐标分别为(4,0),(2,-4),故设此直线的解析式为y=kx+b(k≠0),∴解得故线段A1B1所在直线的函数关系式为y=2x-8.
21.证明:(1)∵直线PM切☉O于点M,∴∠PMO=90°,∵弦AB是直径,∴∠ACB=90°,∴∠ACB=∠PMO,∵AC∥PM,∴∠CAB=∠P,∴△ABC∽△POM. (2)∵△ABC∽△POM,∴=,又AB=2OA,OA=OM,∴=,∴2OA2=OP·BC.
22.(1)证明:连接DO ,∵∠ACB=90°,AC为直径, ∴EC为☉O的切线,又∵ED也为☉O的切线, ∴EC=ED.又∵∠EDO=90°,∴∠BDE+∠ADO=90°,∴∠BDE+∠A=90°,又∵∠B+∠A=90°,∴∠BDE=∠B,∴EB=ED.∴EB=EC,即点E是边BC的中点. (2)解:∵BC,BA分别是☉O的切线和割线,∴BC2=BD·BA , ∴(2EC)2= BD·BA ,即36=2·BA,∴BA=3,在Rt△ABC中,由勾股定理得 AC===3. (3)解:△ABC是等腰直角三角形.理由如下:∵四边形ODEC为正方形,∴∠DOC=∠ACB=90°,即DO∥BC,又∵点E是边BC的中点, ∴BC=2OD=AC,∴△ABC是等腰直角三角形.
23.解:(1)过点B,D作x轴的垂线,垂足分别为点M,N.∵A(5,0),B(2,6),∴OM=BC=2,BM=OC=6,AM=3.∵DN∥BM,∴△AND∽△AMB,∴===,∴DN =2,AN=1, ∴ON=4.∴点D的坐标为(4,2).
∵双曲线y=(x>0)经过点D,∴k=2×4=8.∴双曲线的解析式为y=. (2)∵点E在BC上,∴点E的纵坐标为6.又∵点E在双曲线y=上,∴点E的坐标为,∴CE=.∴S四边形ODBE=S梯形OABC-S△OCE-S△AOD =×(BC+OA)×OC-×OC×CE-×OA×DN =×(2+5)×6-×6×-×5×2=12.∴四边形ODBE的面积为12.
24.解:(1)依题意可得BP=20-4x,CQ=3x.当BP=CQ时,20-4x=3x,∴x=.当x=时,BP=CQ. (2)由题知AP=4x,AB=20,AQ=30-3x,AC=30.所以当PQ∥BC时,有=,即=.解得x=.当x=时,PQ∥BC. (3)能.①当△APQ∽△CQB时,有=,即=,解得x=.②当△APQ∽△CBQ时,有=,即=.解得x=5或x=-10(舍去).综上,当x=或x=5时,△APQ与△CQB相似.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
