全等三角形[上学期]
图片预览




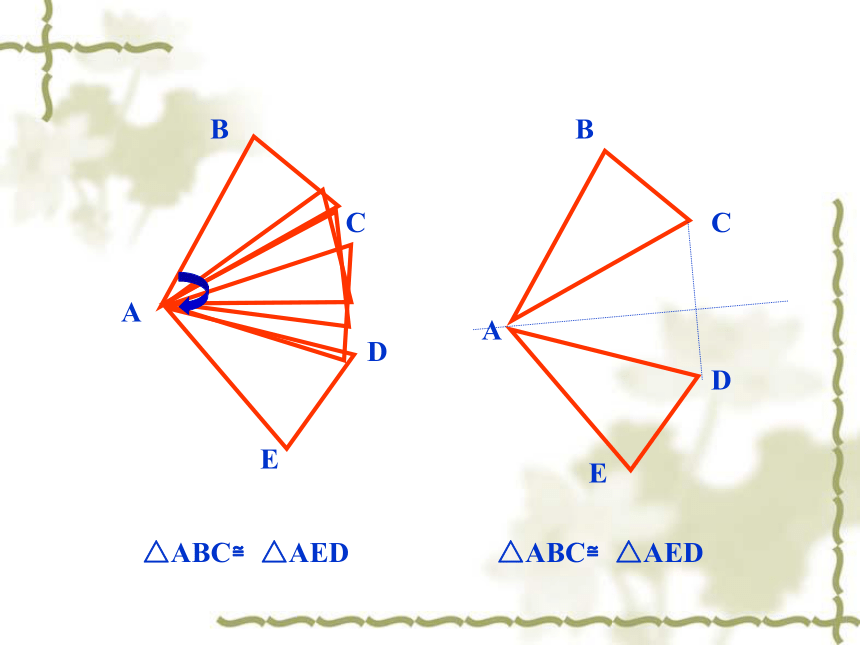
文档简介
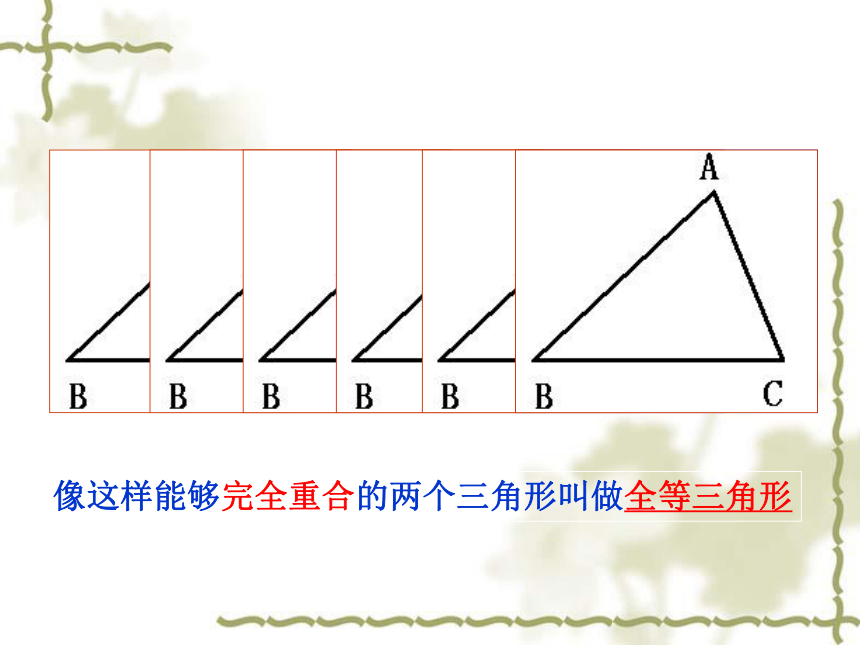
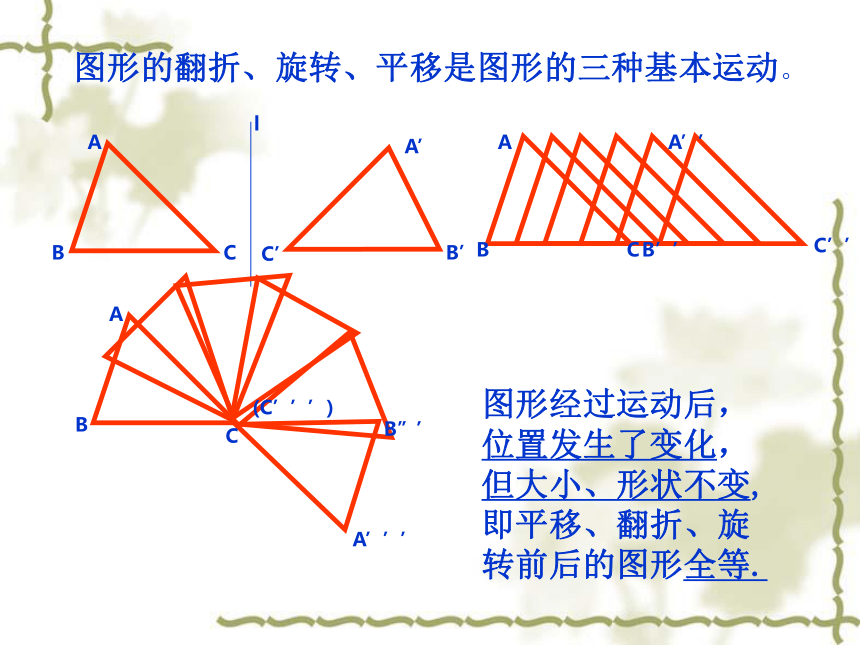
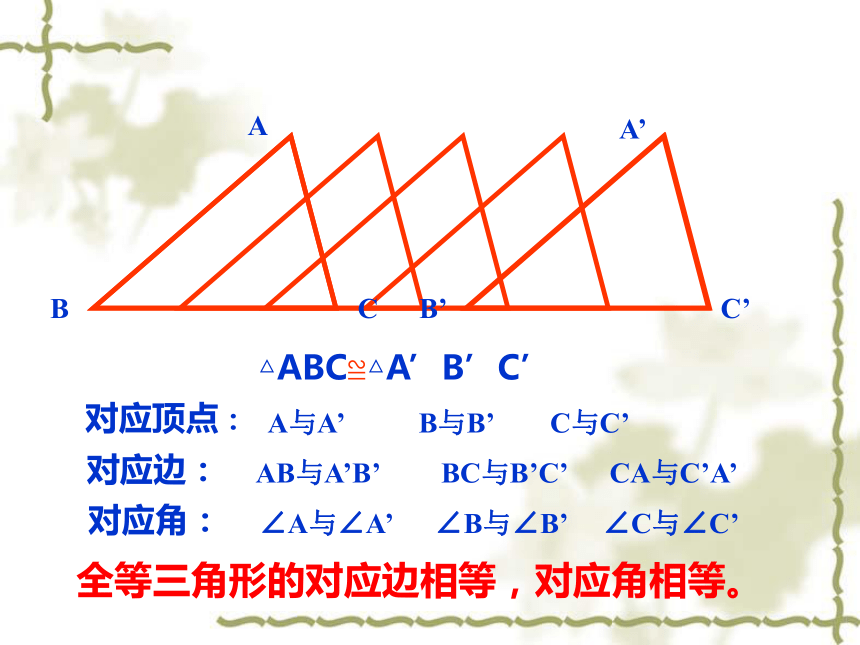
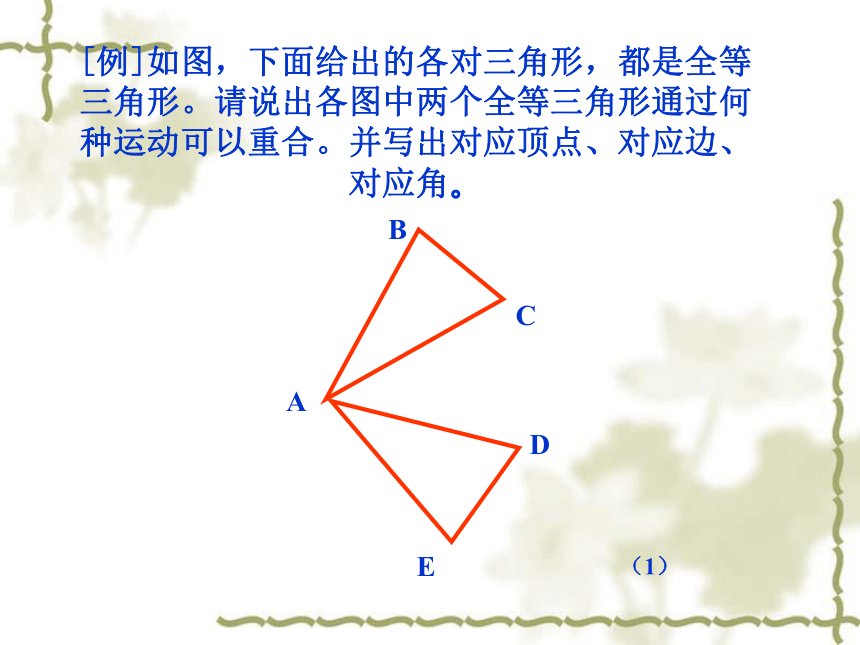
课件22张PPT。13.1 全等三角形同一张底片洗出的照片能够完全重合吗?能够完全重合的两个图形叫全等形像这样能够完全重合的两个三角形叫做全等三角形图形的翻折、旋转、平移是图形的三种基本运动。ABCA’B’C’lAABBCCA’’A’’’B’’B”’C’’(C’’’)图形经过运动后,位置发生了变化,但大小、形状不变,即平移、翻折、旋转前后的图形全等.ABCA’B’C’△ABC≌△A’B’C’A与A’对应顶点:B与B’ C与C’对应边:AB与A’B’BC与B’C’ CA与C’A’对应角:∠A与∠A’ ∠B与∠B’ ∠C与∠C’全等三角形的对应边相等,对应角相等。[例]如图,下面给出的各对三角形,都是全等三角形。请说出各图中两个全等三角形通过何种运动可以重合。并写出对应顶点、对应边、对应角。ABCDE(1)ABCDE△ABC≌△AEDABCDE△ABC≌△AED ABCDFE[例]如图,给出各对三角形,都是全等三角形。 请说出各图中两个全等三角形通过何种运动可 以重合。并写出对应顶点、对应边、对应角。(2) ABCDEF△ABC≌△FDE ABCDEF△ABC≌△FDECBA例1 如图:△ABC≌△ABD,且AC=AD,用等式写出这两个三角形的其它对应边和对应角。 公共边为对应边对应边:BC=BD AB=AB
对应角:∠CAB=∠DAB ∠C=∠D
∠ CBA=∠DBA例2 如图△ABC≌△CDA,AB=CD,用等式写出两个三角形其它的对应边和对应角。
对应边:AD=CB AC=CA
对应角:∠CAB=∠ACD
∠ B=∠D
∠ ACB=∠CAD例2 如图:已知△ABD≌△ACE,且AB=AC,用等式写出两个三角形的其它对应边和对应角。
公共角为对应角对应边:AD=AE BD=CE
对应角:∠A=∠A
∠ADB=∠AEC
∠B=∠CABDEC例4 如图△ABC≌△EDC,∠A=∠E,用等式写出两个三角形其它的对应角和对应边。
对顶角为对应角对应角:∠B=∠D ∠ACB=∠ECD
对应边:AB=ED
AC=EC
BC=DC找全等三角形对应边和对应角的方法:1、从长短大小两个全等三角形的一对最长边(最大角)是对应边(角);一对最短边(最小角)是对应边(角)2、从对应边与对应角的关系对应角所对的边为对应边;对应边所对的角为对应角;两个对应角所夹的边为对应边;两条对应边所夹的角为对应角。3、从位置公共边为对应边;公共角为对应角;对顶角为对应角练习:找出下列各组全等三角形中的对应边及对应角全等三角形的运用举例例1 已知如图△ABC≌△DFE,∠A=96o,∠B=25o,DF=10cm。
求 ∠E的度数及AB的长。
BACEDFEFABCD图5 解:∵△ACF≌△DBE
∠ E=∠F
∴AC=DB
∴AC-BC=DB-BC
即AB=DC
∵AD=9㎝,BC=5㎝
∴AB=2㎝
例3 已知如图 ,△ABE≌△ACD,∠C=20o,AB=10,AD=4,G为AB延长线上的一点。
求 ∠EBG的度数及CE的长。
ECADBGF解:∵△ABE≌△ACD ∠C=20°
∴∠ABE=∠C=20°
∵AB=10 AD=4
∴AC=AB=10 AE=AD=4
∴CE=6再见!
对应角:∠CAB=∠DAB ∠C=∠D
∠ CBA=∠DBA例2 如图△ABC≌△CDA,AB=CD,用等式写出两个三角形其它的对应边和对应角。
对应边:AD=CB AC=CA
对应角:∠CAB=∠ACD
∠ B=∠D
∠ ACB=∠CAD例2 如图:已知△ABD≌△ACE,且AB=AC,用等式写出两个三角形的其它对应边和对应角。
公共角为对应角对应边:AD=AE BD=CE
对应角:∠A=∠A
∠ADB=∠AEC
∠B=∠CABDEC例4 如图△ABC≌△EDC,∠A=∠E,用等式写出两个三角形其它的对应角和对应边。
对顶角为对应角对应角:∠B=∠D ∠ACB=∠ECD
对应边:AB=ED
AC=EC
BC=DC找全等三角形对应边和对应角的方法:1、从长短大小两个全等三角形的一对最长边(最大角)是对应边(角);一对最短边(最小角)是对应边(角)2、从对应边与对应角的关系对应角所对的边为对应边;对应边所对的角为对应角;两个对应角所夹的边为对应边;两条对应边所夹的角为对应角。3、从位置公共边为对应边;公共角为对应角;对顶角为对应角练习:找出下列各组全等三角形中的对应边及对应角全等三角形的运用举例例1 已知如图△ABC≌△DFE,∠A=96o,∠B=25o,DF=10cm。
求 ∠E的度数及AB的长。
BACEDFEFABCD图5 解:∵△ACF≌△DBE
∠ E=∠F
∴AC=DB
∴AC-BC=DB-BC
即AB=DC
∵AD=9㎝,BC=5㎝
∴AB=2㎝
例3 已知如图 ,△ABE≌△ACD,∠C=20o,AB=10,AD=4,G为AB延长线上的一点。
求 ∠EBG的度数及CE的长。
ECADBGF解:∵△ABE≌△ACD ∠C=20°
∴∠ABE=∠C=20°
∵AB=10 AD=4
∴AC=AB=10 AE=AD=4
∴CE=6再见!
