角的平分线的性质[上学期]
文档属性
| 名称 | 角的平分线的性质[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 341.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-10-22 22:39:00 | ||
图片预览

文档简介
(共19张PPT)
13.3角的平分线的性质
2006年10月23日
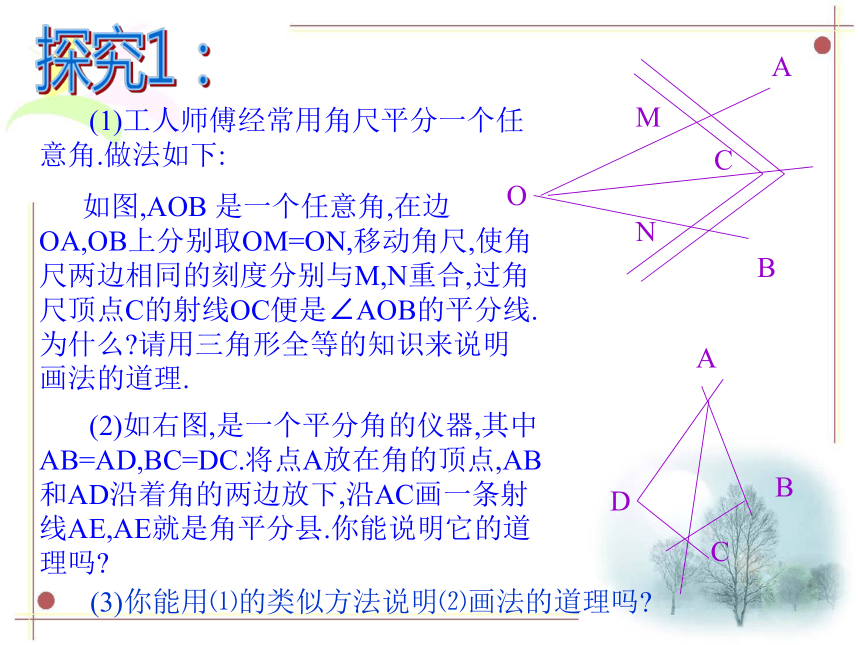
(1)工人师傅经常用角尺平分一个任意角.做法如下:
如图,AOB 是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合,过角尺顶点C的射线OC便是∠AOB的平分线.为什么 请用三角形全等的知识来说明画法的道理.
O
A
B
M
N
C
(2)如右图,是一个平分角的仪器,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分县.你能说明它的道理吗
A
D
C
B
(3)你能用⑴的类似方法说明⑵画法的道理吗
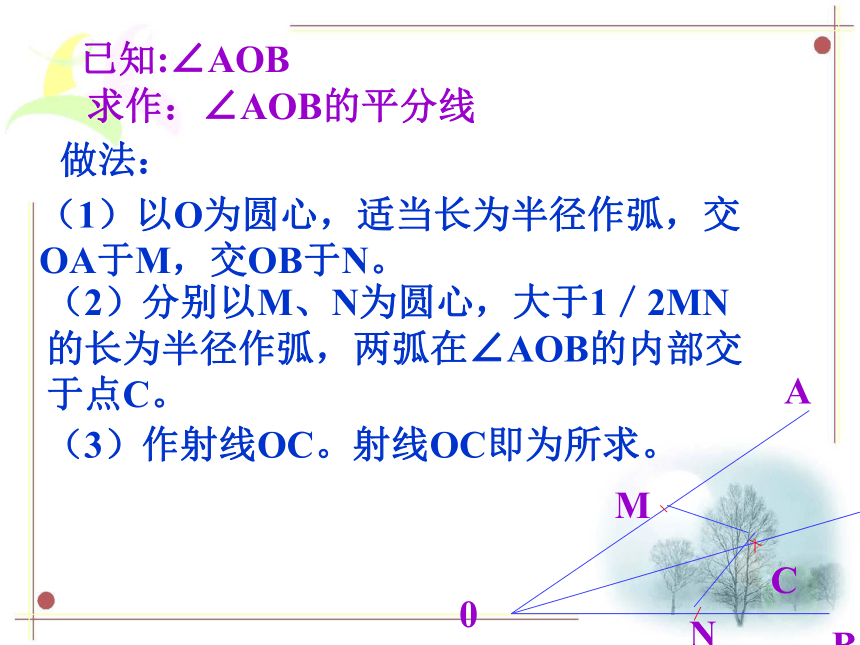
已知:∠AOB
求作:∠AOB的平分线
(1)以O为圆心,适当长为半径作弧,交OA于M,交OB于N。
(2)分别以M、N为圆心,大于1/2MN的长为半径作弧,两弧在∠AOB的内部交于点C。
(3)作射线OC。射线OC即为所求。
A
0
B
M
N
C
做法:
A
B
M
N
C
.
O
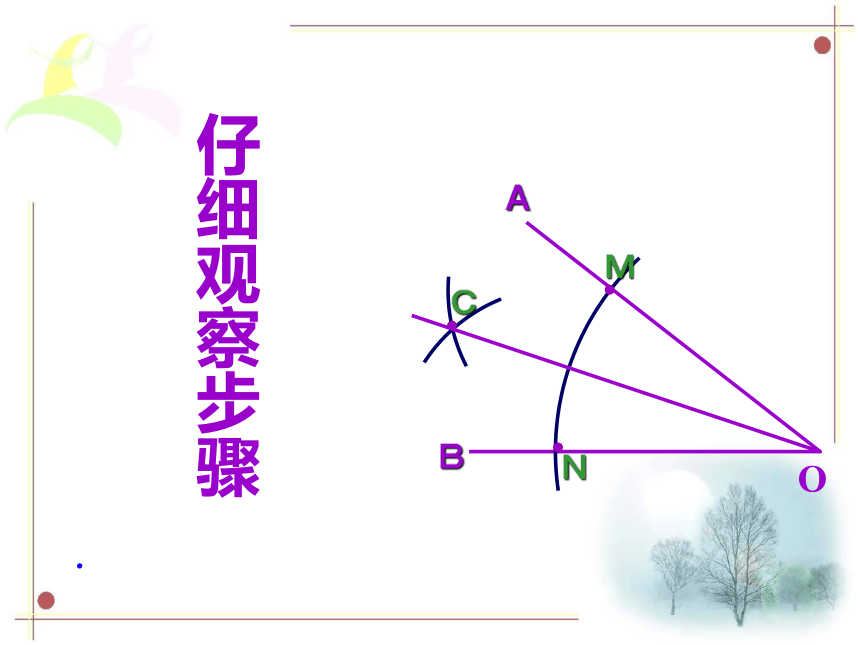
仔细观察步骤
A
B
O
A
O
E
B
C
P
D
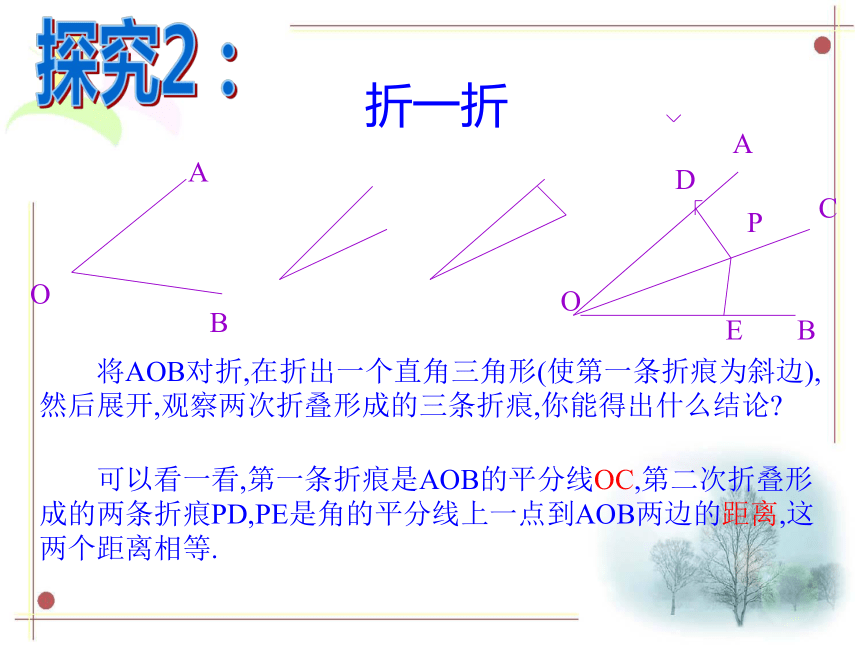
将AOB对折,在折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得出什么结论
可以看一看,第一条折痕是AOB的平分线OC,第二次折叠形成的两条折痕PD,PE是角的平分线上一点到AOB两边的距离,这两个距离相等.
折一折
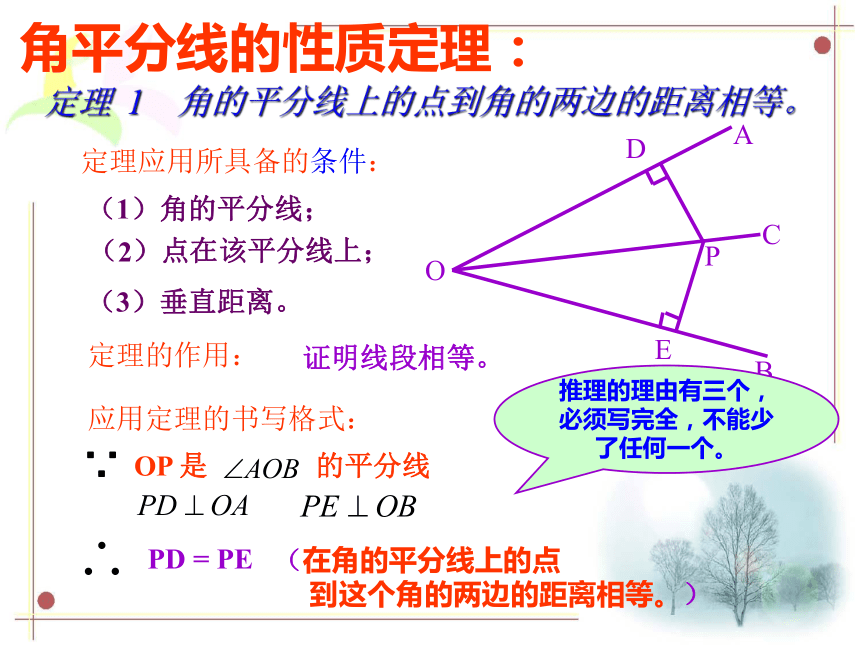
角平分线的性质定理:
定理 1 角的平分线上的点到角的两边的距离相等。
B
A
D
O
P
E
C
定理应用所具备的条件:
(1)角的平分线;
(2)点在该平分线上;
(3)垂直距离。
定理的作用:
证明线段相等。
应用定理的书写格式:
OP 是 的平分线
\
PD = PE
(在角的平分线上的点
到这个角的两边的距离相等。)
∵
推理的理由有三个,必须写完全,不能少了任何一个。
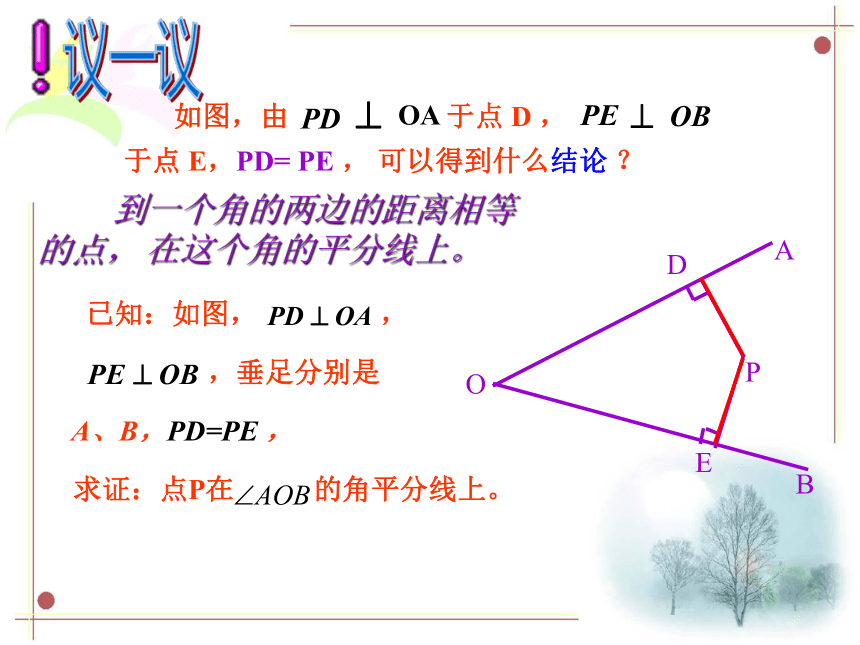
如图,由 于点 D , 于点 E,PD= PE , 可以得到什么结论 ?
OB
PE
^
PD
^
OA
到一个角的两边的距离相等的点, 在这个角的平分线上。
已知:如图, ,
,垂足分别是
A、B,PD=PE ,
求证:点P在 的角平分线上。
B
A
D
O
P
E
到角的两边的距离相等的点 在角的平分线上。
已知:如图, , , 垂足分别是 D、E,PD=PE,
求证:点P在 的角平分线上。
证明:
\
作射线OP
\ 点P在 角的平分线上
在 Rt△PDO 和Rt△PEO 中,
( HL)
\
(全等三角形的对应角相等)
OP = OP (公共边)
PD = PE ( 已 知 )
\
≌
定理 2
B
A
D
O
P
E
∵
定理 2的应用书写格式:
OP 是 的平分线
PD= PE
\
(到一个角的两边的距离相等的点, 在这个角的平分线上)
∵
D
E
O
P
A
B
定理 1 在角的平分线上的点到这个角的两边的距离相等。
定理 2 到一个角的两边的距离相等的点, 在这个角的平分线上。
B
A
D
O
P
E
C
\
PD = PE
OP 是 的平分线
∵
∵
\
OP 是 的平分线
PD = PE
用途:证线段相等
用途:判定一条射线是角平分线
∵ 如图,AD平分∠BAC(已知)
∴ = ,( )
在角的平分线上的点到这个角的两边的距离相等。
BD CD
(×)
∵ 如图, DC⊥AC,DB⊥AB (已知)
∴ = ,( )
在角的平分线上的点到这个角的两边的距离相等。
BD CD
(×)
∵ AD平分∠BAC, DC⊥AC,DB⊥AB (已知)
∴ = ,( )
DB
DC
在角的平分线上的点到这个角的两边的距离相等。
√
不必再证全等
3、△ABC中, ∠C=900,AD平分∠ CAB,且
BC=8,BD=5,求点D到AB的距离是多少?
A
B
C
D
E
已知:如图,△ABC的角平分线BM、CN相交于点P. 求证:点P到三边AB、BC、CA的距离相等.
例题讲解:
B
A
C
P
N
M
证明:过点P作PD 、PE、PF分别垂直于AB、BC、CA,垂足为D、E、F
(在角平分线上的点到角的两边的距离相等)
同理 PE=PF.
∴ PD=PE=PF.
即点P到边AB、BC、 CA的距离相等
∵BM是△ABC的角平分线,点P在BM上
∴PD=PE
1 如图,DE⊥AB,DF⊥BC,垂足分别是E,F, DE =DF, ∠EDB= 60°,则 ∠EBF= 度,BE= 。
60
BF
2 如图,在△ABC中,∠C=90°,DE⊥AB,∠1=∠2,且AC=6cm,那么线段BE是△ABC的 ,AE+DE= 。
角的平分线
AC
(1)角平分线的性质定理及其逆定理及作用;
(2)用这两个定理,一定要具备两个垂直距离(即点到直线的距离),证明过程中要直接应用这两个定理,而不要去寻找全等三角形(这样做实际是重新证了一次定理)。
小结:
(3)怎样找三角形内到三角形三边距离相等的点。
A
B
C
P
P110第3、4 、5题
设计者:沈海尉
2006年10月23日
13.3角的平分线的性质
2006年10月23日
(1)工人师傅经常用角尺平分一个任意角.做法如下:
如图,AOB 是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合,过角尺顶点C的射线OC便是∠AOB的平分线.为什么 请用三角形全等的知识来说明画法的道理.
O
A
B
M
N
C
(2)如右图,是一个平分角的仪器,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分县.你能说明它的道理吗
A
D
C
B
(3)你能用⑴的类似方法说明⑵画法的道理吗
已知:∠AOB
求作:∠AOB的平分线
(1)以O为圆心,适当长为半径作弧,交OA于M,交OB于N。
(2)分别以M、N为圆心,大于1/2MN的长为半径作弧,两弧在∠AOB的内部交于点C。
(3)作射线OC。射线OC即为所求。
A
0
B
M
N
C
做法:
A
B
M
N
C
.
O
仔细观察步骤
A
B
O
A
O
E
B
C
P
D
将AOB对折,在折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得出什么结论
可以看一看,第一条折痕是AOB的平分线OC,第二次折叠形成的两条折痕PD,PE是角的平分线上一点到AOB两边的距离,这两个距离相等.
折一折
角平分线的性质定理:
定理 1 角的平分线上的点到角的两边的距离相等。
B
A
D
O
P
E
C
定理应用所具备的条件:
(1)角的平分线;
(2)点在该平分线上;
(3)垂直距离。
定理的作用:
证明线段相等。
应用定理的书写格式:
OP 是 的平分线
\
PD = PE
(在角的平分线上的点
到这个角的两边的距离相等。)
∵
推理的理由有三个,必须写完全,不能少了任何一个。
如图,由 于点 D , 于点 E,PD= PE , 可以得到什么结论 ?
OB
PE
^
PD
^
OA
到一个角的两边的距离相等的点, 在这个角的平分线上。
已知:如图, ,
,垂足分别是
A、B,PD=PE ,
求证:点P在 的角平分线上。
B
A
D
O
P
E
到角的两边的距离相等的点 在角的平分线上。
已知:如图, , , 垂足分别是 D、E,PD=PE,
求证:点P在 的角平分线上。
证明:
\
作射线OP
\ 点P在 角的平分线上
在 Rt△PDO 和Rt△PEO 中,
( HL)
\
(全等三角形的对应角相等)
OP = OP (公共边)
PD = PE ( 已 知 )
\
≌
定理 2
B
A
D
O
P
E
∵
定理 2的应用书写格式:
OP 是 的平分线
PD= PE
\
(到一个角的两边的距离相等的点, 在这个角的平分线上)
∵
D
E
O
P
A
B
定理 1 在角的平分线上的点到这个角的两边的距离相等。
定理 2 到一个角的两边的距离相等的点, 在这个角的平分线上。
B
A
D
O
P
E
C
\
PD = PE
OP 是 的平分线
∵
∵
\
OP 是 的平分线
PD = PE
用途:证线段相等
用途:判定一条射线是角平分线
∵ 如图,AD平分∠BAC(已知)
∴ = ,( )
在角的平分线上的点到这个角的两边的距离相等。
BD CD
(×)
∵ 如图, DC⊥AC,DB⊥AB (已知)
∴ = ,( )
在角的平分线上的点到这个角的两边的距离相等。
BD CD
(×)
∵ AD平分∠BAC, DC⊥AC,DB⊥AB (已知)
∴ = ,( )
DB
DC
在角的平分线上的点到这个角的两边的距离相等。
√
不必再证全等
3、△ABC中, ∠C=900,AD平分∠ CAB,且
BC=8,BD=5,求点D到AB的距离是多少?
A
B
C
D
E
已知:如图,△ABC的角平分线BM、CN相交于点P. 求证:点P到三边AB、BC、CA的距离相等.
例题讲解:
B
A
C
P
N
M
证明:过点P作PD 、PE、PF分别垂直于AB、BC、CA,垂足为D、E、F
(在角平分线上的点到角的两边的距离相等)
同理 PE=PF.
∴ PD=PE=PF.
即点P到边AB、BC、 CA的距离相等
∵BM是△ABC的角平分线,点P在BM上
∴PD=PE
1 如图,DE⊥AB,DF⊥BC,垂足分别是E,F, DE =DF, ∠EDB= 60°,则 ∠EBF= 度,BE= 。
60
BF
2 如图,在△ABC中,∠C=90°,DE⊥AB,∠1=∠2,且AC=6cm,那么线段BE是△ABC的 ,AE+DE= 。
角的平分线
AC
(1)角平分线的性质定理及其逆定理及作用;
(2)用这两个定理,一定要具备两个垂直距离(即点到直线的距离),证明过程中要直接应用这两个定理,而不要去寻找全等三角形(这样做实际是重新证了一次定理)。
小结:
(3)怎样找三角形内到三角形三边距离相等的点。
A
B
C
P
P110第3、4 、5题
设计者:沈海尉
2006年10月23日
