2022年九年级上册《旋转》专项练习(含解析)
文档属性
| 名称 | 2022年九年级上册《旋转》专项练习(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-19 22:06:09 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2022年九年级上册《旋转》专项练习
1.(2022 渝北区自主招生)下列常用手机APP的图标中,是中心对称图形的是( )
A. B. C. D.
2.(2022春 胶州市期中)如图,在平面直角坐标系中,点A的坐标为(﹣2,3),将点A绕原点O逆时针方向旋转90°得到点B,则点B的坐标为( )
A.(﹣2,﹣3) B.(﹣3,﹣2) C.(2,3) D.(3,2)
3.(2022春 萧山区期中)点A(x+2y,1)与点B(2x﹣y,y)关于原点成中心对称,则x的值为( )
A.0 B.1 C. D.3
4.(2021 贺州)在平面直角坐标系中,点A(3,2)关于原点对称的点的坐标是( )
A.(﹣3,2) B.(3,﹣2) C.(﹣2,﹣3) D.(﹣3,﹣2)
5.(2022春 锦江区校级期中)如图,△AOB中,∠B=25°,将△AOB绕点O顺时针旋转60°,得到△A′OB′,边A′B′与边OB交于点C(A′不在OB上),则∠A′CO的度数为( )
A.105° B.95° C.85° D.75°
6.(2022春 济阳区期末)如图,在Rt△ABC中,∠B=90°,BC=6,AB=9,将△ABC绕点A顺时针旋转90°得到△AB'C',连接CC',则CC'的长为( )
A. B. C. D.
7.(2021秋 江汉区期中)如图,在△ABC中,AB=AC,∠BAC=50°,将△ABC绕着点A顺时针方向旋转得△ADE,AB,CE相交于点F,若AD∥CE时,则∠BAE的大小是( )
A.20° B.25° C.30° D.35°
8.(2021秋 天门期中)如图,在Rt△ABC,∠B=90°,∠ACB=50°,将Rt△ABC在平面内绕点A逆时针旋转到△AB′C′的位置,连接CC′.若AB∥CC′,则旋转角的度数为( )
A.90° B.100° C.105° D.88°
9.(2021秋 江汉区期中)如图,C为线段AB的中点,D为AB垂直平分线上一点,连接BD,将BD绕点D顺时针旋转60°得到线段DE,连接AE,若AB=2,AE=4,则CD的长为 .
10.(2021秋 汉川市期中)如图,已知点P是等边△ABC内一点,PA=4,PB=3,PC=5.将线段AP绕点A逆时针旋转60°得到AQ,连接PQ,CQ.则△PQC的面积为 .
11.(2021秋 章贡区期末)如图,△AOB中,OA=4,OB=6,,将△AOB绕原点O顺时针旋转90°,则旋转后点A的对应点A'的坐标是 .
12.(2021秋 赤壁市期中)如图,△ABC是边长为2的等边三角形,点D为BC边上的中点,以点D为顶点作正方形DEFG,且DE=BC,连接AE,AG.若将正方形DEFG绕点D旋转一周,当AE取最小值时,AG的长为 .
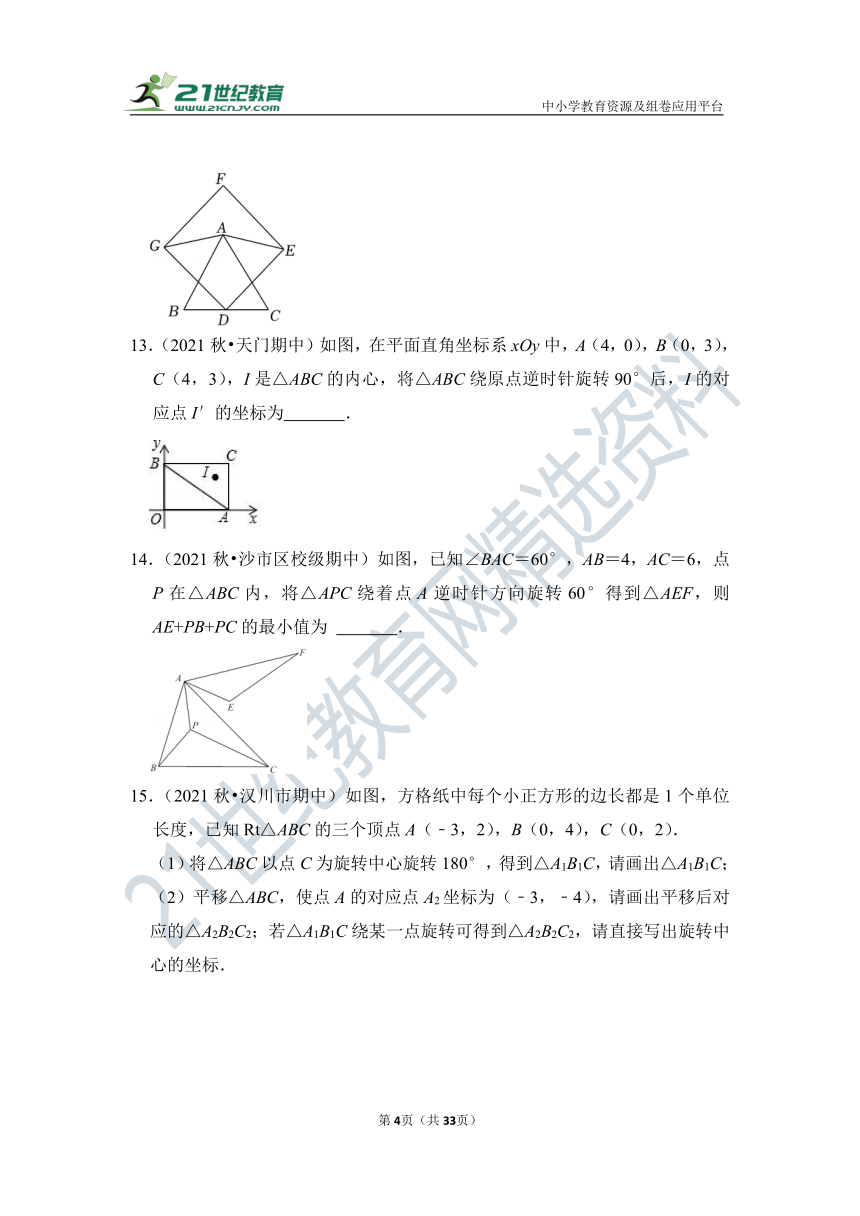
13.(2021秋 天门期中)如图,在平面直角坐标系xOy中,A(4,0),B(0,3),C(4,3),I是△ABC的内心,将△ABC绕原点逆时针旋转90°后,I的对应点I′的坐标为 .
14.(2021秋 沙市区校级期中)如图,已知∠BAC=60°,AB=4,AC=6,点P在△ABC内,将△APC绕着点A逆时针方向旋转60°得到△AEF,则AE+PB+PC的最小值为 .
15.(2021秋 汉川市期中)如图,方格纸中每个小正方形的边长都是1个单位长度,已知Rt△ABC的三个顶点A(﹣3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C;
(2)平移△ABC,使点A的对应点A2坐标为(﹣3,﹣4),请画出平移后对应的△A2B2C2;若△A1B1C绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标.
16.(2021秋 汉川市期中)在等腰直角三角形ABC中,∠BAC=90°,点E、F分别为AB,AC的中点,H为线段EF上一动点(不与点E,F重合),将线段AH绕点A逆时针方向旋转90°得到AG,连接GC,HB.
(1)如图1,求证:△AHB≌△AGC;
(2)如图2,连接GF,HG,HG交AF于点Q.
①点H在运动的过程中,求证:∠HFG=90°;
②若AB=AC=4,当△AQG为等腰三角形时,EH的长为 .
17.(2021秋 赤壁市期中)如图,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,将△ADF绕点A顺时针旋转90°得到△ABG.
(1)求证:△EAG≌△EAF;
(2)若正方形ABCD的边长为6,DF=3,则BE= .
18.(2021 房县一模)(1)问题发现:
如图(1),△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,点B在线段AE上,点C在线段AD上,请直接写出线段BE与线段CD的数量关系: ;
(2)操作探究:
如图(2),将图(1)中的△ABC绕点A顺时针旋转α(0°<α<360°),请判断并证明线段BE与线段CD的数量关系;
(3)解决问题:
将图(1)中的△ABC绕点A顺时针旋转α(0°<α<360°),若DE=2AC,在旋转的过程中,当以A、B、C、D四点为顶点的四边形是平行四边形时,请直接写出旋转角α的度数.
19.(2021秋 河口县期末)如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣4,3)、B(﹣3,1)、C(﹣1,3).
(1)请按下列要求画图:
①将△ABC先向右平移4个单位长度、再向上平移2个单位长度,得到△A1B1C1,画出△A1B1C1;
②△A2B2C2与△ABC关于原点O成中心对称,画出△A2B2C2.
(2)在(1)中所得的△A1B1C1和△A2B2C2关于点M成中心对称,请写出对称中心M点的坐标 .
20.(2021秋 天门期中)如图,△ABC中,∠BAC=120°,以BC为边向外作等边△BCD,把△ABD绕着D点按顺时针方向旋转60°后到△ECD的位置,且点A、C、E在同一直线上.若AB=6,AC=4,求∠BAD的度数和AD的长.
21.(2021秋 十堰期中)在等腰△OAB和等腰△OCD中,OA=OB,OC=OD,连接AC、BD交于点M.
(1)如图1.若∠AOB=∠COD=40°.则AC与BD的数量关系为 ;∠AMB的度数为 ;
(2)如图2,若∠AOB=∠COD=90°,判断AC与BD之间存在怎样的关系?并说明理由;
(3)在(2)的条件下,当∠ABC=60°,且点C与点M重合时,请直接写出OD与OA之间存在的数量关系.
22.(2019秋 铁力市期末)如图,△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=α,AC、BD交于M.
(1)如图1,当α=90°时,∠AMD的度数为 °;
(2)如图2,当α=60°时,求∠AMD的度数;
(3)如图3,当△OCD绕O点任意旋转时,∠AMD与α是否存在着确定的数量关系?如果存在,请你用α表示∠AMD,并用图3进行证明;若不确定,说明理由.
2022年九年级上册《旋转》专项练习
参考答案与试题解析
1.(2022 渝北区自主招生)下列常用手机APP的图标中,是中心对称图形的是( )
A. B. C. D.
【解答】解:选项A、B、D不能找到这样的一个点,使图形绕某一点旋转180°后与原来的图形重合,所以不是中心对称图形,
选项C能找到这样的一个点,使图形绕某一点旋转180°后与原来的图形重合,所以是中心对称图形,
故选:C.
2.(2022春 胶州市期中)如图,在平面直角坐标系中,点A的坐标为(﹣2,3),将点A绕原点O逆时针方向旋转90°得到点B,则点B的坐标为( )
A.(﹣2,﹣3) B.(﹣3,﹣2) C.(2,3) D.(3,2)
【解答】解:过A点作AD⊥y轴,过B点作BE⊥x轴,
∵点A的坐标为(﹣2,3),
∴AD=2,OD=3,
∵∠AOB=90°,
∴∠AOD+∠AOE=90°,
∴∠BOE+∠AOE=90°,
∴∠AOD=∠BOE,
∵OA=OB,
在△AOD和△BOE中,
,
∴△AOD≌△BOE(AAS),
∵BE=AD=2,OA=OD=3
∴点A的坐标为(﹣3,﹣2),
故选:B.
3.(2022春 萧山区期中)点A(x+2y,1)与点B(2x﹣y,y)关于原点成中心对称,则x的值为( )
A.0 B.1 C. D.3
【解答】解:∵点A(x+2y,1)与点B(2x﹣y,y)关于原点成中心对称,
∴,
解得,
∴x的值为,
故选:C.
4.(2021 贺州)在平面直角坐标系中,点A(3,2)关于原点对称的点的坐标是( )
A.(﹣3,2) B.(3,﹣2) C.(﹣2,﹣3) D.(﹣3,﹣2)
【解答】解:点(3,2)关于原点对称的点的坐标是:(﹣3,﹣2).
故选:D.
5.(2022春 锦江区校级期中)如图,△AOB中,∠B=25°,将△AOB绕点O顺时针旋转60°,得到△A′OB′,边A′B′与边OB交于点C(A′不在OB上),则∠A′CO的度数为( )
A.105° B.95° C.85° D.75°
【解答】解:∵将△AOB绕点O顺时针旋转60°,得到△A′OB′,
∴∠B=∠B'=25°,∠BOB'=60°,
∴∠A'CO=∠B'+∠BOB'=85°,
故选:C.
6.(2022春 济阳区期末)如图,在Rt△ABC中,∠B=90°,BC=6,AB=9,将△ABC绕点A顺时针旋转90°得到△AB'C',连接CC',则CC'的长为( )
A. B. C. D.
【解答】解:∵∠B=90°,BC=6,AB=9,
∴AC====3,
由旋转得:AC=AC',∠CAC'=90°,
∴CC'===3.
故选:D.
7.(2021秋 江汉区期中)如图,在△ABC中,AB=AC,∠BAC=50°,将△ABC绕着点A顺时针方向旋转得△ADE,AB,CE相交于点F,若AD∥CE时,则∠BAE的大小是( )
A.20° B.25° C.30° D.35°
【解答】解:∵将△ABC绕着点A顺时针方向旋转得△ADE,
∴∠DAE=∠BAC=50°,AC=AE,
∵AD∥CE,
∴∠DAE=∠AEC=50°,
∴∠ACE=∠AEC=50°,
∴∠EAC=180°﹣∠AEC﹣∠ACE=180°﹣50°﹣50°=80°,
∴∠BAE=∠EAC﹣∠BAC=80°﹣50°=30°.
故选:C.
8.(2021秋 天门期中)如图,在Rt△ABC,∠B=90°,∠ACB=50°,将Rt△ABC在平面内绕点A逆时针旋转到△AB′C′的位置,连接CC′.若AB∥CC′,则旋转角的度数为( )
A.90° B.100° C.105° D.88°
【解答】解:∵AB∥CC',
∴∠ABC+∠C′CB=180°,
而∠B=90°,
∴∠C′CB=90°,
∴∠ACC′=90°﹣∠ACB=90°﹣50°=40°,
∵Rt△ABC在平面内绕点A逆时针旋转到△AB'C'的位置,
∴AC=AC′,∠C′AC等于旋转角,
∴∠AC′C=∠ACC′=40°,
∴∠C′AC=180°﹣40°﹣40°=100°,
即旋转角为100°.
故选:B.
9.(2021秋 江汉区期中)如图,C为线段AB的中点,D为AB垂直平分线上一点,连接BD,将BD绕点D顺时针旋转60°得到线段DE,连接AE,若AB=2,AE=4,则CD的长为 7 .
【解答】解:连接AD,过D作DF⊥AE于F,延长BA交DF的延长线于H,
∵D为AB垂直平分线上一点,AB=2,
∴BD=AD,AC=AB=,
∴∠ADC=ADB,
∵将BD绕点D顺时针旋转60°得到线段DE,
∴DE=BD,
∴DE=AD,
∴∠ADF=ADE,AF=AE=2,
∴∠HDC=∠ADF+∠ADC=BDE=30°,
∵∠HCD=∠AFH=90°,
∴∠H=60°,
∴∠CDH=30°,AH=,
∴CH=AH+AC=,
∴CD=CH=7,
故答案为:7.
10.(2021秋 汉川市期中)如图,已知点P是等边△ABC内一点,PA=4,PB=3,PC=5.将线段AP绕点A逆时针旋转60°得到AQ,连接PQ,CQ.则△PQC的面积为 6 .
【解答】解:∵线段AP绕点A逆时针旋转60°到AQ,
∴AP=AQ,∠PAQ=60°,
∴△APQ是等边三角形,∠PAC+∠CAQ=60°,
∵△ABC是等边三角形,
∴∠BAP+∠PAC=60°,AB=AC,
∴∠BAP=∠CAQ,
在△BAP和△CAQ中,
,
∴△BAP≌△CAQ(SAS);
∴BP=QC=3,
∵AP=PQ=4,PC=5.
∴32+42=52,
∴QC2+PQ2=PC2,
∴△PQC是直角三角形,
∴∠PQC=90°,
∴△PQC的面积=PQ QC=4×3=6.
故答案为:6.
11.(2021秋 章贡区期末)如图,△AOB中,OA=4,OB=6,,将△AOB绕原点O顺时针旋转90°,则旋转后点A的对应点A'的坐标是 (2,﹣2) .
【解答】解:如图,过点A作AH⊥OB于H,设OH=m,则BH=6﹣m,
∵AH2=OA2﹣OH2=AB2﹣BH2,
∴42﹣m2=(2)2﹣(6﹣m)2,
∴m=2,
∴AH==2,
∴A(2,2),
∴将△AOB绕原点O逆时针旋转90°,则旋转后点A的对应点A′(2,﹣2),
故答案为:(2,﹣2).
12.(2021秋 赤壁市期中)如图,△ABC是边长为2的等边三角形,点D为BC边上的中点,以点D为顶点作正方形DEFG,且DE=BC,连接AE,AG.若将正方形DEFG绕点D旋转一周,当AE取最小值时,AG的长为 .
【解答】解:连接AD,
∵△ABC是边长为2的等边三角形,点D为BC边上的中点,
∴BD=CD==1,AD⊥BC,
在Rt△ABD中,AD==,
当点E在DA延长线上时,AE=DE﹣AD.
此时AE取最小值,
在Rt△ADG中,AG===,
故答案为:.
13.(2021秋 天门期中)如图,在平面直角坐标系xOy中,A(4,0),B(0,3),C(4,3),I是△ABC的内心,将△ABC绕原点逆时针旋转90°后,I的对应点I′的坐标为 (﹣2,3) .
【解答】解:过点作IF⊥AC于点F,IE⊥OA于点E,
∵A(4,0),B(0,3),C(4,3),
∴BC=4,AC=3,
则AB=5,
∵I是△ABC的内心,
∴I到△ABC各边距离相等,等于其内切圆的半径,
∴IF=1,故I到BC的距离也为1,
则AE=1,
故IE=3﹣1=2,
OE=4﹣1=3,
则I(3,2),
∵△ABC绕原点逆时针旋转90°,
∴I的对应点I'的坐标为:(﹣2,3).
故答案为:(﹣2,3).
14.(2021秋 沙市区校级期中)如图,已知∠BAC=60°,AB=4,AC=6,点P在△ABC内,将△APC绕着点A逆时针方向旋转60°得到△AEF,则AE+PB+PC的最小值为 2 .
【解答】解:连接PE,BF,过点F作FH⊥BA,交BA的延长线于H,
∵将△APC绕着点A逆时针方向旋转60°得到△AEF,
∴AP=AE,AC=AF,∠PAE=∠CAF=60°,
∴△APE是等边三角形,
∴AE=PE,
∴当点B、P、E、F共线时,AE+PB+PC最小,最小值为BF的长,
∵∠BAF=∠BAC+∠CAF=60°+60°=120°,
∴∠FAH=60°,
∴AH=3,FH=3,
∴BH=AB+AH=4+3=7,
在Rt△BFH中,由勾股定理得,
BF==2,
∴AE+PB+PC的最小值为2,
故答案为:2.
15.(2021秋 汉川市期中)如图,方格纸中每个小正方形的边长都是1个单位长度,已知Rt△ABC的三个顶点A(﹣3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C;
(2)平移△ABC,使点A的对应点A2坐标为(﹣3,﹣4),请画出平移后对应的△A2B2C2;若△A1B1C绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标.
【解答】解:(1)如图,△A1B1C为所作;
(2)如图,△A2B2C2为所作;旋转中心的坐标为(0,﹣1).
16.(2021秋 汉川市期中)在等腰直角三角形ABC中,∠BAC=90°,点E、F分别为AB,AC的中点,H为线段EF上一动点(不与点E,F重合),将线段AH绕点A逆时针方向旋转90°得到AG,连接GC,HB.
(1)如图1,求证:△AHB≌△AGC;
(2)如图2,连接GF,HG,HG交AF于点Q.
①点H在运动的过程中,求证:∠HFG=90°;
②若AB=AC=4,当△AQG为等腰三角形时,EH的长为 或2 .
【解答】解:(1)证明:由旋转得:AH=AG,∠HAG=90°,
∵∠BAC=90°,
∴∠BAH=90°﹣∠HAC=∠CAG,
∴∠BAH=∠CAG,
∵AB=AC,
∴△ABH≌△ACG(SAS);
(2)①证明:在等腰直角三角形ABC中,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∵点E,F分别为AB,AC的中点,
∴EF是△ABC的中位线,
∴EF∥BC,,,
∴AE=AF,∠AEF=∠ABC=45°,∠AFE=∠ACB=45°,
∵∠EAH=∠FAG=90°﹣∠HAF,AH=AG,
∴△AEH≌△AFG(SAS),
∴∠AFG=∠AEH=45°,
∴∠HFG=45°+45°=90°;
②分两种情况:
i)如图3,AQ=QG时,
∵AQ=QG,
∴∠QAG=∠AGQ,
∵∠HAG=∠HAQ+∠QAG=∠AHG+∠AGH=90°,
∴∠QAH=∠AHQ,
∴AQ=QH=QG,
∵AH=AG,
∴AQ⊥GH,
∵∠AFG=∠AFH=45°,
∴∠FGQ=∠FHQ=45°,
∴∠HFG=∠AGF=∠AHF=90°,
∴四边形AHFG是正方形,
∵AC=4,
∴AF=2,
∴FG=EH=,
∴当EH的长度为时,△AQG为等腰三角形;
ii)如图4,当AG=QG时,∠GAQ=∠AQG,
∵∠AEH=∠AGQ=45°,∠EAH=∠GAQ,
∴∠AHE=∠AQG=∠EAH,
∴EH=AE=2,
∴当EH的长度为2时,△AQG为等腰三角形;
综上,当EH的长度为或2时,△AQG为等腰三角形.
故答案为:或2.
17.(2021秋 赤壁市期中)如图,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,将△ADF绕点A顺时针旋转90°得到△ABG.
(1)求证:△EAG≌△EAF;
(2)若正方形ABCD的边长为6,DF=3,则BE= 2 .
【解答】(1)证明:∵将△ADF绕点A顺时针旋转90°得到△ABG,
∴△ADF≌△ABG,
∴AG=AF,∠DAF=∠BAG,
∵∠DAB=90°,∠EAF=45°,
∴∠DAF+∠EAB=45°,
∴∠BAG+∠EAB=45°,
即∠EAF=∠EAG,
在△EAG和△EAF中,
,
∴△EAG≌△EAF(SAS);
(2)解:设BE=x,则EF=GE=3+x,CE=6﹣x,
∵CD=6,DF=3,
∴CF=CD﹣DF=3,
∵∠C=90°,
∴(6﹣x)2+32=(3+x)2,
解得,x=2,
即BE=2.
故答案为:2.
18.(2021 房县一模)(1)问题发现:
如图(1),△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,点B在线段AE上,点C在线段AD上,请直接写出线段BE与线段CD的数量关系: BE=CD ;
(2)操作探究:
如图(2),将图(1)中的△ABC绕点A顺时针旋转α(0°<α<360°),请判断并证明线段BE与线段CD的数量关系;
(3)解决问题:
将图(1)中的△ABC绕点A顺时针旋转α(0°<α<360°),若DE=2AC,在旋转的过程中,当以A、B、C、D四点为顶点的四边形是平行四边形时,请直接写出旋转角α的度数.
【解答】解:(1)∵△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,
∴AB=AC,AE=AD,
∴AE﹣AB=AD﹣AC,
∴BE=CD;
(2)∵△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,
∴AB=AC,AE=AD,
由旋转的性质得,∠BAE=∠CAD,
在△BAE与△CAD中,,
∴△BAE≌△CAD(SAS)
∴BE=CD;
(3)如图,
∵以A、B、C、D四点为顶点的四边形是平行四边形,△ABC和△AED都是等腰直角三角形,
∴∠ABC=∠ADC=45°,
∵ED=2AC,
∴AC=CD,
∴∠CAD=45°
或360°﹣90°﹣45°=225°,或360°﹣45°=315°
∴角α的度数是45°或225°或315°.
故答案为:BE=CD.
19.(2021秋 河口县期末)如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣4,3)、B(﹣3,1)、C(﹣1,3).
(1)请按下列要求画图:
①将△ABC先向右平移4个单位长度、再向上平移2个单位长度,得到△A1B1C1,画出△A1B1C1;
②△A2B2C2与△ABC关于原点O成中心对称,画出△A2B2C2.
(2)在(1)中所得的△A1B1C1和△A2B2C2关于点M成中心对称,请写出对称中心M点的坐标 (2,1) .
【解答】解:(1)①如图,△A1B1C1即为所求;
②如图,△A2B2C2即为所求;
(2)如图,点M即为所求,M(2,1),
故答案为:(2,1).
20.(2021秋 天门期中)如图,△ABC中,∠BAC=120°,以BC为边向外作等边△BCD,把△ABD绕着D点按顺时针方向旋转60°后到△ECD的位置,且点A、C、E在同一直线上.若AB=6,AC=4,求∠BAD的度数和AD的长.
【解答】解:∵把△ABD绕点D按顺时针方向旋转60°后到△ECD的位置,
∴AD=DE,∠ADE=60°,AB=CE,
∵∠BDC+∠BAC=60°+120°=180°,
∴∠ABD+∠ACD=180°,
∵∠ABD=∠DCE,
∴∠ACD+∠DCE=180°,
∴A,C,E在一条直线上,
∴△ADE是等边三角形,
∴∠DAE=60°,
∴∠BAD=120°﹣60°=60°;
∴AE=AD=AC+EC=AC+AB=10.
21.(2021秋 十堰期中)在等腰△OAB和等腰△OCD中,OA=OB,OC=OD,连接AC、BD交于点M.
(1)如图1.若∠AOB=∠COD=40°.则AC与BD的数量关系为 AC=BD ;∠AMB的度数为 40° ;
(2)如图2,若∠AOB=∠COD=90°,判断AC与BD之间存在怎样的关系?并说明理由;
(3)在(2)的条件下,当∠ABC=60°,且点C与点M重合时,请直接写出OD与OA之间存在的数量关系.
【解答】解:(1)∵∠AOB=∠COD,
∴∠AOB+∠AOD=∠COD+∠AOD,
∴∠BOD=∠AOC,
在△BOD和△AOC中,
,
∴△BOD≌△AOC(SAS),
∴AC=BD;∠OBD=∠OAC,
∵∠AOB=40°,
∴∠OAB+∠OBA=180°﹣∠AOB=180°﹣40°=140°,
又∵∠OAB+∠OBA=∠OAB+∠ABD+∠OBD,
∴∠OAB+∠OBA=∠OAB+∠ABD+∠OAC=140°,
∴∠MAB+ABM=140°,
∵在△ABM中,∠AMB+∠MAB+ABM=180°,
∴∠AMB=40°,
故答案为:AC=BD,40°;
(2)AC=BD,AC⊥BD,
理由如下:∵∠AOB=∠COD=90°,
∴∠AOB+∠AOD=∠COD+∠AOD,
∴∠BOD=∠AOC,
在△BOD和△AOC中,
,
∴△BOD≌△AOC(SAS),
∴BD=AC,∠OBD=∠OAC,
又∵∠OAB+∠OBA=90°,
∠ABO=∠ABM+∠OBD,
∠MAB=∠MAO+∠OAB,
∴∠MAB+∠MBA=90°,
又∵在△AMB中,∠AMB+∠ABM+∠BAM=180°,
∴∠AMB=180°﹣(∠ABM+∠BAM)=180°﹣90°=90°,
∴AC⊥BD;
(3)如图3所示,∠AOB=∠COD=90°,OA=OB,OC=OD,∠ABC=30°,
∵C,M重合,
∴B,C,D共线,
∴∠OAB=∠OBA=∠OCD=∠ODC=45°,AB=OA,CD=OC,
由(2)得△BOD≌△AOC(SAS),
∴∠ACO=∠BDO=45°,BD=AC,
∴∠ACD=∠ACO+∠OCD=90°,
∴∠ACB=90°,
∴BC=AB,
由勾股定理得:AC==AB,
∴CD=AC﹣BC=AB,
∴OC=×OA,
∴OD=OC=OA.
如图4,同上易求得OD=OC=OA,
综上所述,OD=OA或OD=OA.
22.(2019秋 铁力市期末)如图,△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=α,AC、BD交于M.
(1)如图1,当α=90°时,∠AMD的度数为 90 °;
(2)如图2,当α=60°时,求∠AMD的度数;
(3)如图3,当△OCD绕O点任意旋转时,∠AMD与α是否存在着确定的数量关系?如果存在,请你用α表示∠AMD,并用图3进行证明;若不确定,说明理由.
【解答】解:(1)如图1中,设OA交BD于K.
∵∠AOB=∠COD=α,
∴∠BOD=∠AOC,
在△BOD和△AOC中,
,
∴△BOD≌△AOC(SAS),
∴∠OBD=∠OAC,
∵∠AKM=∠BKO,
∴∠AMK=∠BOK=90°,
∴∠AMD=180°﹣90°=90°.
故答案为90.
(2)如图2中,设OA交BD于K.
∵∠AOB=∠COD=α,
∴∠BOD=∠AOC,
在△BOD和△AOC中,
,
∴△BOD≌△AOC(SAS),
∴∠OBD=∠OAC,
∵∠AKM=∠BKO,
∴∠AMK=∠BOK=60°,
∴∠AMD=180°﹣60°=120°;
(3)如图3中,设OA交BD于K.
∵∠AOB=∠COD=α,
∴∠BOD=∠AOC,
在△BOD和△AOC中,
,
∴△BOD≌△AOC(SAS),
∴∠OBD=∠OAC,
∵∠AKO=∠BKM,
∴∠AOK=∠BMK=α.
∴∠AMD=180°﹣α.
第1页(共1页)
2022年九年级上册《旋转》专项练习
1.(2022 渝北区自主招生)下列常用手机APP的图标中,是中心对称图形的是( )
A. B. C. D.
2.(2022春 胶州市期中)如图,在平面直角坐标系中,点A的坐标为(﹣2,3),将点A绕原点O逆时针方向旋转90°得到点B,则点B的坐标为( )
A.(﹣2,﹣3) B.(﹣3,﹣2) C.(2,3) D.(3,2)
3.(2022春 萧山区期中)点A(x+2y,1)与点B(2x﹣y,y)关于原点成中心对称,则x的值为( )
A.0 B.1 C. D.3
4.(2021 贺州)在平面直角坐标系中,点A(3,2)关于原点对称的点的坐标是( )
A.(﹣3,2) B.(3,﹣2) C.(﹣2,﹣3) D.(﹣3,﹣2)
5.(2022春 锦江区校级期中)如图,△AOB中,∠B=25°,将△AOB绕点O顺时针旋转60°,得到△A′OB′,边A′B′与边OB交于点C(A′不在OB上),则∠A′CO的度数为( )
A.105° B.95° C.85° D.75°
6.(2022春 济阳区期末)如图,在Rt△ABC中,∠B=90°,BC=6,AB=9,将△ABC绕点A顺时针旋转90°得到△AB'C',连接CC',则CC'的长为( )
A. B. C. D.
7.(2021秋 江汉区期中)如图,在△ABC中,AB=AC,∠BAC=50°,将△ABC绕着点A顺时针方向旋转得△ADE,AB,CE相交于点F,若AD∥CE时,则∠BAE的大小是( )
A.20° B.25° C.30° D.35°
8.(2021秋 天门期中)如图,在Rt△ABC,∠B=90°,∠ACB=50°,将Rt△ABC在平面内绕点A逆时针旋转到△AB′C′的位置,连接CC′.若AB∥CC′,则旋转角的度数为( )
A.90° B.100° C.105° D.88°
9.(2021秋 江汉区期中)如图,C为线段AB的中点,D为AB垂直平分线上一点,连接BD,将BD绕点D顺时针旋转60°得到线段DE,连接AE,若AB=2,AE=4,则CD的长为 .
10.(2021秋 汉川市期中)如图,已知点P是等边△ABC内一点,PA=4,PB=3,PC=5.将线段AP绕点A逆时针旋转60°得到AQ,连接PQ,CQ.则△PQC的面积为 .
11.(2021秋 章贡区期末)如图,△AOB中,OA=4,OB=6,,将△AOB绕原点O顺时针旋转90°,则旋转后点A的对应点A'的坐标是 .
12.(2021秋 赤壁市期中)如图,△ABC是边长为2的等边三角形,点D为BC边上的中点,以点D为顶点作正方形DEFG,且DE=BC,连接AE,AG.若将正方形DEFG绕点D旋转一周,当AE取最小值时,AG的长为 .
13.(2021秋 天门期中)如图,在平面直角坐标系xOy中,A(4,0),B(0,3),C(4,3),I是△ABC的内心,将△ABC绕原点逆时针旋转90°后,I的对应点I′的坐标为 .
14.(2021秋 沙市区校级期中)如图,已知∠BAC=60°,AB=4,AC=6,点P在△ABC内,将△APC绕着点A逆时针方向旋转60°得到△AEF,则AE+PB+PC的最小值为 .
15.(2021秋 汉川市期中)如图,方格纸中每个小正方形的边长都是1个单位长度,已知Rt△ABC的三个顶点A(﹣3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C;
(2)平移△ABC,使点A的对应点A2坐标为(﹣3,﹣4),请画出平移后对应的△A2B2C2;若△A1B1C绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标.
16.(2021秋 汉川市期中)在等腰直角三角形ABC中,∠BAC=90°,点E、F分别为AB,AC的中点,H为线段EF上一动点(不与点E,F重合),将线段AH绕点A逆时针方向旋转90°得到AG,连接GC,HB.
(1)如图1,求证:△AHB≌△AGC;
(2)如图2,连接GF,HG,HG交AF于点Q.
①点H在运动的过程中,求证:∠HFG=90°;
②若AB=AC=4,当△AQG为等腰三角形时,EH的长为 .
17.(2021秋 赤壁市期中)如图,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,将△ADF绕点A顺时针旋转90°得到△ABG.
(1)求证:△EAG≌△EAF;
(2)若正方形ABCD的边长为6,DF=3,则BE= .
18.(2021 房县一模)(1)问题发现:
如图(1),△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,点B在线段AE上,点C在线段AD上,请直接写出线段BE与线段CD的数量关系: ;
(2)操作探究:
如图(2),将图(1)中的△ABC绕点A顺时针旋转α(0°<α<360°),请判断并证明线段BE与线段CD的数量关系;
(3)解决问题:
将图(1)中的△ABC绕点A顺时针旋转α(0°<α<360°),若DE=2AC,在旋转的过程中,当以A、B、C、D四点为顶点的四边形是平行四边形时,请直接写出旋转角α的度数.
19.(2021秋 河口县期末)如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣4,3)、B(﹣3,1)、C(﹣1,3).
(1)请按下列要求画图:
①将△ABC先向右平移4个单位长度、再向上平移2个单位长度,得到△A1B1C1,画出△A1B1C1;
②△A2B2C2与△ABC关于原点O成中心对称,画出△A2B2C2.
(2)在(1)中所得的△A1B1C1和△A2B2C2关于点M成中心对称,请写出对称中心M点的坐标 .
20.(2021秋 天门期中)如图,△ABC中,∠BAC=120°,以BC为边向外作等边△BCD,把△ABD绕着D点按顺时针方向旋转60°后到△ECD的位置,且点A、C、E在同一直线上.若AB=6,AC=4,求∠BAD的度数和AD的长.
21.(2021秋 十堰期中)在等腰△OAB和等腰△OCD中,OA=OB,OC=OD,连接AC、BD交于点M.
(1)如图1.若∠AOB=∠COD=40°.则AC与BD的数量关系为 ;∠AMB的度数为 ;
(2)如图2,若∠AOB=∠COD=90°,判断AC与BD之间存在怎样的关系?并说明理由;
(3)在(2)的条件下,当∠ABC=60°,且点C与点M重合时,请直接写出OD与OA之间存在的数量关系.
22.(2019秋 铁力市期末)如图,△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=α,AC、BD交于M.
(1)如图1,当α=90°时,∠AMD的度数为 °;
(2)如图2,当α=60°时,求∠AMD的度数;
(3)如图3,当△OCD绕O点任意旋转时,∠AMD与α是否存在着确定的数量关系?如果存在,请你用α表示∠AMD,并用图3进行证明;若不确定,说明理由.
2022年九年级上册《旋转》专项练习
参考答案与试题解析
1.(2022 渝北区自主招生)下列常用手机APP的图标中,是中心对称图形的是( )
A. B. C. D.
【解答】解:选项A、B、D不能找到这样的一个点,使图形绕某一点旋转180°后与原来的图形重合,所以不是中心对称图形,
选项C能找到这样的一个点,使图形绕某一点旋转180°后与原来的图形重合,所以是中心对称图形,
故选:C.
2.(2022春 胶州市期中)如图,在平面直角坐标系中,点A的坐标为(﹣2,3),将点A绕原点O逆时针方向旋转90°得到点B,则点B的坐标为( )
A.(﹣2,﹣3) B.(﹣3,﹣2) C.(2,3) D.(3,2)
【解答】解:过A点作AD⊥y轴,过B点作BE⊥x轴,
∵点A的坐标为(﹣2,3),
∴AD=2,OD=3,
∵∠AOB=90°,
∴∠AOD+∠AOE=90°,
∴∠BOE+∠AOE=90°,
∴∠AOD=∠BOE,
∵OA=OB,
在△AOD和△BOE中,
,
∴△AOD≌△BOE(AAS),
∵BE=AD=2,OA=OD=3
∴点A的坐标为(﹣3,﹣2),
故选:B.
3.(2022春 萧山区期中)点A(x+2y,1)与点B(2x﹣y,y)关于原点成中心对称,则x的值为( )
A.0 B.1 C. D.3
【解答】解:∵点A(x+2y,1)与点B(2x﹣y,y)关于原点成中心对称,
∴,
解得,
∴x的值为,
故选:C.
4.(2021 贺州)在平面直角坐标系中,点A(3,2)关于原点对称的点的坐标是( )
A.(﹣3,2) B.(3,﹣2) C.(﹣2,﹣3) D.(﹣3,﹣2)
【解答】解:点(3,2)关于原点对称的点的坐标是:(﹣3,﹣2).
故选:D.
5.(2022春 锦江区校级期中)如图,△AOB中,∠B=25°,将△AOB绕点O顺时针旋转60°,得到△A′OB′,边A′B′与边OB交于点C(A′不在OB上),则∠A′CO的度数为( )
A.105° B.95° C.85° D.75°
【解答】解:∵将△AOB绕点O顺时针旋转60°,得到△A′OB′,
∴∠B=∠B'=25°,∠BOB'=60°,
∴∠A'CO=∠B'+∠BOB'=85°,
故选:C.
6.(2022春 济阳区期末)如图,在Rt△ABC中,∠B=90°,BC=6,AB=9,将△ABC绕点A顺时针旋转90°得到△AB'C',连接CC',则CC'的长为( )
A. B. C. D.
【解答】解:∵∠B=90°,BC=6,AB=9,
∴AC====3,
由旋转得:AC=AC',∠CAC'=90°,
∴CC'===3.
故选:D.
7.(2021秋 江汉区期中)如图,在△ABC中,AB=AC,∠BAC=50°,将△ABC绕着点A顺时针方向旋转得△ADE,AB,CE相交于点F,若AD∥CE时,则∠BAE的大小是( )
A.20° B.25° C.30° D.35°
【解答】解:∵将△ABC绕着点A顺时针方向旋转得△ADE,
∴∠DAE=∠BAC=50°,AC=AE,
∵AD∥CE,
∴∠DAE=∠AEC=50°,
∴∠ACE=∠AEC=50°,
∴∠EAC=180°﹣∠AEC﹣∠ACE=180°﹣50°﹣50°=80°,
∴∠BAE=∠EAC﹣∠BAC=80°﹣50°=30°.
故选:C.
8.(2021秋 天门期中)如图,在Rt△ABC,∠B=90°,∠ACB=50°,将Rt△ABC在平面内绕点A逆时针旋转到△AB′C′的位置,连接CC′.若AB∥CC′,则旋转角的度数为( )
A.90° B.100° C.105° D.88°
【解答】解:∵AB∥CC',
∴∠ABC+∠C′CB=180°,
而∠B=90°,
∴∠C′CB=90°,
∴∠ACC′=90°﹣∠ACB=90°﹣50°=40°,
∵Rt△ABC在平面内绕点A逆时针旋转到△AB'C'的位置,
∴AC=AC′,∠C′AC等于旋转角,
∴∠AC′C=∠ACC′=40°,
∴∠C′AC=180°﹣40°﹣40°=100°,
即旋转角为100°.
故选:B.
9.(2021秋 江汉区期中)如图,C为线段AB的中点,D为AB垂直平分线上一点,连接BD,将BD绕点D顺时针旋转60°得到线段DE,连接AE,若AB=2,AE=4,则CD的长为 7 .
【解答】解:连接AD,过D作DF⊥AE于F,延长BA交DF的延长线于H,
∵D为AB垂直平分线上一点,AB=2,
∴BD=AD,AC=AB=,
∴∠ADC=ADB,
∵将BD绕点D顺时针旋转60°得到线段DE,
∴DE=BD,
∴DE=AD,
∴∠ADF=ADE,AF=AE=2,
∴∠HDC=∠ADF+∠ADC=BDE=30°,
∵∠HCD=∠AFH=90°,
∴∠H=60°,
∴∠CDH=30°,AH=,
∴CH=AH+AC=,
∴CD=CH=7,
故答案为:7.
10.(2021秋 汉川市期中)如图,已知点P是等边△ABC内一点,PA=4,PB=3,PC=5.将线段AP绕点A逆时针旋转60°得到AQ,连接PQ,CQ.则△PQC的面积为 6 .
【解答】解:∵线段AP绕点A逆时针旋转60°到AQ,
∴AP=AQ,∠PAQ=60°,
∴△APQ是等边三角形,∠PAC+∠CAQ=60°,
∵△ABC是等边三角形,
∴∠BAP+∠PAC=60°,AB=AC,
∴∠BAP=∠CAQ,
在△BAP和△CAQ中,
,
∴△BAP≌△CAQ(SAS);
∴BP=QC=3,
∵AP=PQ=4,PC=5.
∴32+42=52,
∴QC2+PQ2=PC2,
∴△PQC是直角三角形,
∴∠PQC=90°,
∴△PQC的面积=PQ QC=4×3=6.
故答案为:6.
11.(2021秋 章贡区期末)如图,△AOB中,OA=4,OB=6,,将△AOB绕原点O顺时针旋转90°,则旋转后点A的对应点A'的坐标是 (2,﹣2) .
【解答】解:如图,过点A作AH⊥OB于H,设OH=m,则BH=6﹣m,
∵AH2=OA2﹣OH2=AB2﹣BH2,
∴42﹣m2=(2)2﹣(6﹣m)2,
∴m=2,
∴AH==2,
∴A(2,2),
∴将△AOB绕原点O逆时针旋转90°,则旋转后点A的对应点A′(2,﹣2),
故答案为:(2,﹣2).
12.(2021秋 赤壁市期中)如图,△ABC是边长为2的等边三角形,点D为BC边上的中点,以点D为顶点作正方形DEFG,且DE=BC,连接AE,AG.若将正方形DEFG绕点D旋转一周,当AE取最小值时,AG的长为 .
【解答】解:连接AD,
∵△ABC是边长为2的等边三角形,点D为BC边上的中点,
∴BD=CD==1,AD⊥BC,
在Rt△ABD中,AD==,
当点E在DA延长线上时,AE=DE﹣AD.
此时AE取最小值,
在Rt△ADG中,AG===,
故答案为:.
13.(2021秋 天门期中)如图,在平面直角坐标系xOy中,A(4,0),B(0,3),C(4,3),I是△ABC的内心,将△ABC绕原点逆时针旋转90°后,I的对应点I′的坐标为 (﹣2,3) .
【解答】解:过点作IF⊥AC于点F,IE⊥OA于点E,
∵A(4,0),B(0,3),C(4,3),
∴BC=4,AC=3,
则AB=5,
∵I是△ABC的内心,
∴I到△ABC各边距离相等,等于其内切圆的半径,
∴IF=1,故I到BC的距离也为1,
则AE=1,
故IE=3﹣1=2,
OE=4﹣1=3,
则I(3,2),
∵△ABC绕原点逆时针旋转90°,
∴I的对应点I'的坐标为:(﹣2,3).
故答案为:(﹣2,3).
14.(2021秋 沙市区校级期中)如图,已知∠BAC=60°,AB=4,AC=6,点P在△ABC内,将△APC绕着点A逆时针方向旋转60°得到△AEF,则AE+PB+PC的最小值为 2 .
【解答】解:连接PE,BF,过点F作FH⊥BA,交BA的延长线于H,
∵将△APC绕着点A逆时针方向旋转60°得到△AEF,
∴AP=AE,AC=AF,∠PAE=∠CAF=60°,
∴△APE是等边三角形,
∴AE=PE,
∴当点B、P、E、F共线时,AE+PB+PC最小,最小值为BF的长,
∵∠BAF=∠BAC+∠CAF=60°+60°=120°,
∴∠FAH=60°,
∴AH=3,FH=3,
∴BH=AB+AH=4+3=7,
在Rt△BFH中,由勾股定理得,
BF==2,
∴AE+PB+PC的最小值为2,
故答案为:2.
15.(2021秋 汉川市期中)如图,方格纸中每个小正方形的边长都是1个单位长度,已知Rt△ABC的三个顶点A(﹣3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C;
(2)平移△ABC,使点A的对应点A2坐标为(﹣3,﹣4),请画出平移后对应的△A2B2C2;若△A1B1C绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标.
【解答】解:(1)如图,△A1B1C为所作;
(2)如图,△A2B2C2为所作;旋转中心的坐标为(0,﹣1).
16.(2021秋 汉川市期中)在等腰直角三角形ABC中,∠BAC=90°,点E、F分别为AB,AC的中点,H为线段EF上一动点(不与点E,F重合),将线段AH绕点A逆时针方向旋转90°得到AG,连接GC,HB.
(1)如图1,求证:△AHB≌△AGC;
(2)如图2,连接GF,HG,HG交AF于点Q.
①点H在运动的过程中,求证:∠HFG=90°;
②若AB=AC=4,当△AQG为等腰三角形时,EH的长为 或2 .
【解答】解:(1)证明:由旋转得:AH=AG,∠HAG=90°,
∵∠BAC=90°,
∴∠BAH=90°﹣∠HAC=∠CAG,
∴∠BAH=∠CAG,
∵AB=AC,
∴△ABH≌△ACG(SAS);
(2)①证明:在等腰直角三角形ABC中,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∵点E,F分别为AB,AC的中点,
∴EF是△ABC的中位线,
∴EF∥BC,,,
∴AE=AF,∠AEF=∠ABC=45°,∠AFE=∠ACB=45°,
∵∠EAH=∠FAG=90°﹣∠HAF,AH=AG,
∴△AEH≌△AFG(SAS),
∴∠AFG=∠AEH=45°,
∴∠HFG=45°+45°=90°;
②分两种情况:
i)如图3,AQ=QG时,
∵AQ=QG,
∴∠QAG=∠AGQ,
∵∠HAG=∠HAQ+∠QAG=∠AHG+∠AGH=90°,
∴∠QAH=∠AHQ,
∴AQ=QH=QG,
∵AH=AG,
∴AQ⊥GH,
∵∠AFG=∠AFH=45°,
∴∠FGQ=∠FHQ=45°,
∴∠HFG=∠AGF=∠AHF=90°,
∴四边形AHFG是正方形,
∵AC=4,
∴AF=2,
∴FG=EH=,
∴当EH的长度为时,△AQG为等腰三角形;
ii)如图4,当AG=QG时,∠GAQ=∠AQG,
∵∠AEH=∠AGQ=45°,∠EAH=∠GAQ,
∴∠AHE=∠AQG=∠EAH,
∴EH=AE=2,
∴当EH的长度为2时,△AQG为等腰三角形;
综上,当EH的长度为或2时,△AQG为等腰三角形.
故答案为:或2.
17.(2021秋 赤壁市期中)如图,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,将△ADF绕点A顺时针旋转90°得到△ABG.
(1)求证:△EAG≌△EAF;
(2)若正方形ABCD的边长为6,DF=3,则BE= 2 .
【解答】(1)证明:∵将△ADF绕点A顺时针旋转90°得到△ABG,
∴△ADF≌△ABG,
∴AG=AF,∠DAF=∠BAG,
∵∠DAB=90°,∠EAF=45°,
∴∠DAF+∠EAB=45°,
∴∠BAG+∠EAB=45°,
即∠EAF=∠EAG,
在△EAG和△EAF中,
,
∴△EAG≌△EAF(SAS);
(2)解:设BE=x,则EF=GE=3+x,CE=6﹣x,
∵CD=6,DF=3,
∴CF=CD﹣DF=3,
∵∠C=90°,
∴(6﹣x)2+32=(3+x)2,
解得,x=2,
即BE=2.
故答案为:2.
18.(2021 房县一模)(1)问题发现:
如图(1),△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,点B在线段AE上,点C在线段AD上,请直接写出线段BE与线段CD的数量关系: BE=CD ;
(2)操作探究:
如图(2),将图(1)中的△ABC绕点A顺时针旋转α(0°<α<360°),请判断并证明线段BE与线段CD的数量关系;
(3)解决问题:
将图(1)中的△ABC绕点A顺时针旋转α(0°<α<360°),若DE=2AC,在旋转的过程中,当以A、B、C、D四点为顶点的四边形是平行四边形时,请直接写出旋转角α的度数.
【解答】解:(1)∵△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,
∴AB=AC,AE=AD,
∴AE﹣AB=AD﹣AC,
∴BE=CD;
(2)∵△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,
∴AB=AC,AE=AD,
由旋转的性质得,∠BAE=∠CAD,
在△BAE与△CAD中,,
∴△BAE≌△CAD(SAS)
∴BE=CD;
(3)如图,
∵以A、B、C、D四点为顶点的四边形是平行四边形,△ABC和△AED都是等腰直角三角形,
∴∠ABC=∠ADC=45°,
∵ED=2AC,
∴AC=CD,
∴∠CAD=45°
或360°﹣90°﹣45°=225°,或360°﹣45°=315°
∴角α的度数是45°或225°或315°.
故答案为:BE=CD.
19.(2021秋 河口县期末)如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣4,3)、B(﹣3,1)、C(﹣1,3).
(1)请按下列要求画图:
①将△ABC先向右平移4个单位长度、再向上平移2个单位长度,得到△A1B1C1,画出△A1B1C1;
②△A2B2C2与△ABC关于原点O成中心对称,画出△A2B2C2.
(2)在(1)中所得的△A1B1C1和△A2B2C2关于点M成中心对称,请写出对称中心M点的坐标 (2,1) .
【解答】解:(1)①如图,△A1B1C1即为所求;
②如图,△A2B2C2即为所求;
(2)如图,点M即为所求,M(2,1),
故答案为:(2,1).
20.(2021秋 天门期中)如图,△ABC中,∠BAC=120°,以BC为边向外作等边△BCD,把△ABD绕着D点按顺时针方向旋转60°后到△ECD的位置,且点A、C、E在同一直线上.若AB=6,AC=4,求∠BAD的度数和AD的长.
【解答】解:∵把△ABD绕点D按顺时针方向旋转60°后到△ECD的位置,
∴AD=DE,∠ADE=60°,AB=CE,
∵∠BDC+∠BAC=60°+120°=180°,
∴∠ABD+∠ACD=180°,
∵∠ABD=∠DCE,
∴∠ACD+∠DCE=180°,
∴A,C,E在一条直线上,
∴△ADE是等边三角形,
∴∠DAE=60°,
∴∠BAD=120°﹣60°=60°;
∴AE=AD=AC+EC=AC+AB=10.
21.(2021秋 十堰期中)在等腰△OAB和等腰△OCD中,OA=OB,OC=OD,连接AC、BD交于点M.
(1)如图1.若∠AOB=∠COD=40°.则AC与BD的数量关系为 AC=BD ;∠AMB的度数为 40° ;
(2)如图2,若∠AOB=∠COD=90°,判断AC与BD之间存在怎样的关系?并说明理由;
(3)在(2)的条件下,当∠ABC=60°,且点C与点M重合时,请直接写出OD与OA之间存在的数量关系.
【解答】解:(1)∵∠AOB=∠COD,
∴∠AOB+∠AOD=∠COD+∠AOD,
∴∠BOD=∠AOC,
在△BOD和△AOC中,
,
∴△BOD≌△AOC(SAS),
∴AC=BD;∠OBD=∠OAC,
∵∠AOB=40°,
∴∠OAB+∠OBA=180°﹣∠AOB=180°﹣40°=140°,
又∵∠OAB+∠OBA=∠OAB+∠ABD+∠OBD,
∴∠OAB+∠OBA=∠OAB+∠ABD+∠OAC=140°,
∴∠MAB+ABM=140°,
∵在△ABM中,∠AMB+∠MAB+ABM=180°,
∴∠AMB=40°,
故答案为:AC=BD,40°;
(2)AC=BD,AC⊥BD,
理由如下:∵∠AOB=∠COD=90°,
∴∠AOB+∠AOD=∠COD+∠AOD,
∴∠BOD=∠AOC,
在△BOD和△AOC中,
,
∴△BOD≌△AOC(SAS),
∴BD=AC,∠OBD=∠OAC,
又∵∠OAB+∠OBA=90°,
∠ABO=∠ABM+∠OBD,
∠MAB=∠MAO+∠OAB,
∴∠MAB+∠MBA=90°,
又∵在△AMB中,∠AMB+∠ABM+∠BAM=180°,
∴∠AMB=180°﹣(∠ABM+∠BAM)=180°﹣90°=90°,
∴AC⊥BD;
(3)如图3所示,∠AOB=∠COD=90°,OA=OB,OC=OD,∠ABC=30°,
∵C,M重合,
∴B,C,D共线,
∴∠OAB=∠OBA=∠OCD=∠ODC=45°,AB=OA,CD=OC,
由(2)得△BOD≌△AOC(SAS),
∴∠ACO=∠BDO=45°,BD=AC,
∴∠ACD=∠ACO+∠OCD=90°,
∴∠ACB=90°,
∴BC=AB,
由勾股定理得:AC==AB,
∴CD=AC﹣BC=AB,
∴OC=×OA,
∴OD=OC=OA.
如图4,同上易求得OD=OC=OA,
综上所述,OD=OA或OD=OA.
22.(2019秋 铁力市期末)如图,△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=α,AC、BD交于M.
(1)如图1,当α=90°时,∠AMD的度数为 90 °;
(2)如图2,当α=60°时,求∠AMD的度数;
(3)如图3,当△OCD绕O点任意旋转时,∠AMD与α是否存在着确定的数量关系?如果存在,请你用α表示∠AMD,并用图3进行证明;若不确定,说明理由.
【解答】解:(1)如图1中,设OA交BD于K.
∵∠AOB=∠COD=α,
∴∠BOD=∠AOC,
在△BOD和△AOC中,
,
∴△BOD≌△AOC(SAS),
∴∠OBD=∠OAC,
∵∠AKM=∠BKO,
∴∠AMK=∠BOK=90°,
∴∠AMD=180°﹣90°=90°.
故答案为90.
(2)如图2中,设OA交BD于K.
∵∠AOB=∠COD=α,
∴∠BOD=∠AOC,
在△BOD和△AOC中,
,
∴△BOD≌△AOC(SAS),
∴∠OBD=∠OAC,
∵∠AKM=∠BKO,
∴∠AMK=∠BOK=60°,
∴∠AMD=180°﹣60°=120°;
(3)如图3中,设OA交BD于K.
∵∠AOB=∠COD=α,
∴∠BOD=∠AOC,
在△BOD和△AOC中,
,
∴△BOD≌△AOC(SAS),
∴∠OBD=∠OAC,
∵∠AKO=∠BKM,
∴∠AOK=∠BMK=α.
∴∠AMD=180°﹣α.
第1页(共1页)
同课章节目录
