四种命题及其相互关系

课件27张PPT。 1.1.2---1.1.3
四种命题及相互关系 ２、互否命题：如果第一个命题的条件和结论是第二个命题的条件和结论的否定，那么这两个命题叫做互否命题。如果把其中一个命题叫做原命题，那么另一个叫做原命题的否命题。 ３、互为逆否命题：如果第一个命题的条件和结论分别是第二个命题的结论的否定和条件的否定，那么这两个命题叫做互为逆否命题。 １、互逆命题：如果第一个命题的条件（或题设）是第二个命题的结论，且第一个命题的结论是第二个命题的条件，那么这两个命题叫互逆命题。如果把其中一个命题叫做原命题，那么另一个叫做原命题的逆命题。三个概念若p 则q逆否命题：原命题：逆命题：否命题：若q 则p若? p 则? q若? q 则? p判断正误,并说明理由:(1)若原命题是“对顶角相等”,
它的否命题是“对顶角不相等”。
(2)若原命题是“对顶角相等”,
它的否命题是“不成对顶关系的
两个角不相等”。
否命题与命题的否定否命题是用否定条件也否定结论的方式构成新命题。
命题的否定是逻辑联结词“非”作用于判断,只否定结论不否定条件。
对于原命题: 若 p , 则 q 有
否命题: 若┐p , 则┐q 。
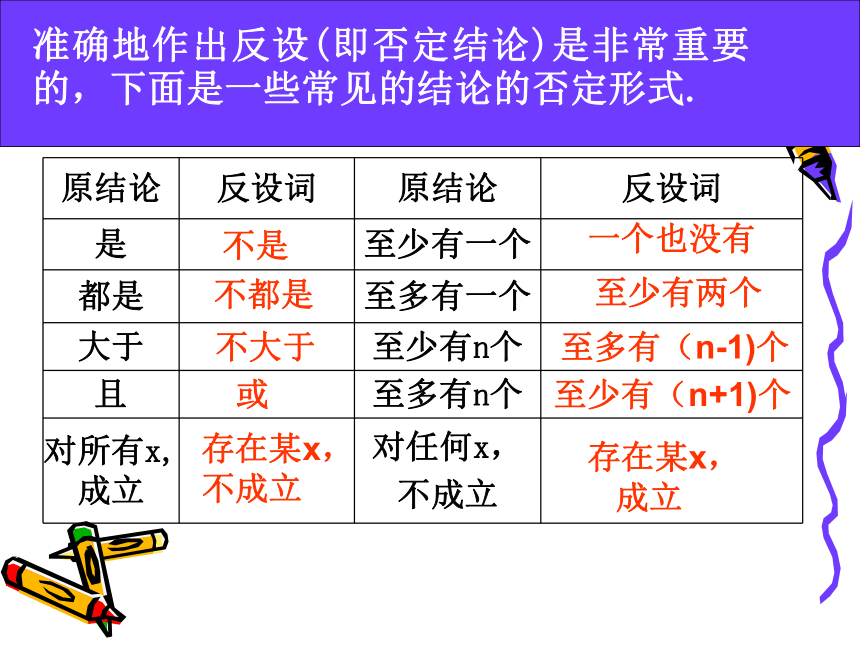
命题的否定: 若 p ，则┐q 。准确地作出反设(即否定结论)是非常重要的，下面是一些常见的结论的否定形式. ?不是不都是不大于或一个也没有至少有两个至多有（n-1)个至少有（n+1)个存在某x，
不成立存在某x，
成立你能说出其中任意两个命题之间的关系吗?
1、四种命题之间的 关系原命题
若p则q逆命题
若q则p否命题
若﹁p则﹁q逆否命题
若﹁q则﹁p互逆互否互否互逆互为 逆否2）原命题：若a=0, 则ab=0。逆命题：若ab=0, 则a=0。否命题：若a≠ 0, 则ab≠0。逆否命题：若ab≠0,则a≠0。(真)(假)(假)(真)(真)2.四种命题的真假看下面的例子：1）原命题：若x=2或x=3, 则x2-5x+6=0。逆命题：若x2-5x+6=0, 则x=2或x=3。否命题：若x≠2且x≠3, 则x2-5x+6≠0 。逆否命题：若x2-5x+6≠0，则x≠2且x≠3。(真)(真)(真)3) 原命题：若a > b, 则 ac2>bc2。逆命题：若ac2>bc2,则a>b。否命题：若a≤b,则ac2≤bc2。逆否命题：若ac2≤bc2,则a≤b。（假）（真）（真）（假） 一般地,四种命题的真假性,有而且仅有下面四种情况:想一想？（2） 若其逆命题为真，则其否命题一定为真。但其原命题、逆否命题不一定为真。由以上三例及总结我们能发现什么？即(1)原命题与逆否命题同真假。(2)原命题的逆命题与否命题同真假。（1） 原命题为真，则其逆否命题一定为真。但其逆命题、否命题不一定为真。总结：(两个命题为互逆命题或互否命题,它们的真假性没有关系).2．四种命题的真假判断
(1)原命题为真，它的逆命题可以为真，也可以为假．
(2)原命题为真，它的否命题可以为真，也可以为假．
(3)原命题为真，它的逆否命题一定为真．
(4)互为逆否的命题是等价命题，它们同真同假，同一个命题的逆命题和否命题是一对互为逆否的命题，所以它们同真同假．
[特别提醒]　原命题的逆命题和原命题的否命题的真假性相同．想一想
1.判断若x2≠9，则x≠3是否正确？
提示：正确．利用逆否命题判断．练一练1.判断下列说法是否正确。1）一个命题的逆命题为真，它的逆否命题不一定为真；（对）2）一个命题的否命题为真，它的逆命题一定为真。（对）2.四种命题真假的个数可能为（ ）个。答：0个、2个、4个。如：原命题：若A∪B=A, 则A∩B=φ。逆命题：若A∩B=φ，则A∪B=A。否命题：若A∪B≠A，则A∩B≠φ。逆否命题：若A∩B≠φ，则A∪B≠A。（假）（假）（假）（假）3）一个命题的原命题为假，它的逆命题一定为假。（错）4）一个命题的逆否命题为假，它的否命题为假。（错）例题讲解例1：设原命题是：当c>0时，若a>b,
则ac>bc. 写出它的逆命题、否命题、逆否命题。并分别判断它们的真假。解：逆命题：当c>0时，若ac>bc, 则a>b.否命题：当c>0时，若a≤b, 则ac≤bc.逆否命题：当c>0时，若ac≤bc, 则a≤b.（真）（真）（真）分析：“当c>0时”是大前提，写其它命题时应该保留。原命题的条件是“a>b”，结论是“ac>bc”。
例2 若m≤0或n≤0，则m+n≤0。写出其逆命题、否命题、逆否命题，并分别指出其假。分析：搞清四种命题的定义及其关系，注意“且” “或”的
否定为“或” “且”。解：逆命题：若m+n≤0，则m≤0或n≤0。否命题：若m>0且n>0, 则m+n>0.逆否命题：若m+n>0, 则m>0且n>0.（真）（真）（假）小结：在判断四种命题的真假时，只需判断两种命题的
真假。因为逆命题与否命题真假等价，逆否命题与原命
题真假等价。 证明：已知函数f(x)是(－∞，＋∞)上的增函数，a、b∈R，若f(a)＋f(b)≥f(－a)＋f(－b)，则a＋b≥0.
【思路点拨】　借助互为逆否的两个命题的真假性相同证明．法二：假设a＋b<0，则a<－b，b<－a，
又∵f(x)在(－∞，＋∞)上是增函数，
∴f(a)∴f(a)＋f(b)这与已知条件f(a)＋f(b)≥f(－a)＋f(－b)相矛盾．因此假设不成立，故a＋b≥0【证明】　法一：原命题的逆否命题为“已知函数f(x)是(－∞，＋∞)上的增函数，a、b∈R，
若a＋b<0，则f(a)＋f(b)若a＋b<0，则a<－b，b<－a，
利用逆否命题可是本题的关键！又∵f(x)在(－∞，＋∞)上是增函数，
∴f(a)∴f(a)＋f(b)即逆否命题为真命题．∴原命题为真命题．【名师点评】　由于原命题和它的逆否命题有相同的真假性，即互为逆否命题的命题具有等价性，所以我们在直接证明某一个命题为真命题有困难时，可以通过证明它的逆否命题为真命题，来间接地证明原命题为真命题．证明：一个三角形中不能有
两个角是直角．已知：△ABC．引例求证：∠A、∠B、∠C中不能
有两个角是直角．3.反证法的一般步骤：假设命题的结论不成立,即假
设结论的反面成立； 从这个假设出发，经过推理论证，得出矛盾； (3) 由矛盾判定假设不正确，
从而肯定命题的结论正确。 反
证
法证： 假设
若_________时,则___________,
∴x2+y2>0与 x2+y2=0矛盾,
若_________时,则___________,
∴x2+y2>0与 x2+y2=0矛盾,
所以假设不成立,
从而______________成立。x、y至少有一个不为0x ≠ 0x2 > 0例3 证明：若x2+y2=0, 则y ≠ 0y2 > 0x =y=0。x =y=0。反证法证明证： 假设_________或_________,
由于____________时,_________________,
与 (x-a)(x-b)≠0矛盾,
又_________时,_________________,
与(x-a)(x-b)≠0矛盾,
所以假设不成立,
从而_________________。x=a x=bx=a (x-a)(x-b)=0x=b(x-a)(x-b)=0x ≠a且x ≠b用反证法证明,若(x-a)(x-b)≠0,则x ≠a且x ≠b. 证明：已知函数f(x)是(－∞，＋∞)上的增函数，a、b∈R，若f(a)＋f(b)≥f(－a)＋f(－b)，则a＋b≥0.
【思路点拨】　借助互为逆否的两个命题的真假性相同证明．法二：假设a＋b<0，则a<－b，b<－a，
又∵f(x)在(－∞，＋∞)上是增函数，
∴f(a)∴f(a)＋f(b)这与已知条件f(a)＋f(b)≥f(－a)＋f(－b)相矛盾．因此假设不成立，故a＋b≥0总结提炼1.用反证法证明命题的一般步骤是什么? 用反证法在归谬中所导出的矛盾可以是与题设矛盾,与假设矛盾,与已知定义、公理、定理矛盾，自相矛盾等．①反设 ②归谬 ③结论2.用反证法证题,矛盾的主要类型有哪些?小结： 1. 四种命题的关系
2. 四种命题的真假关系
3. 一种思想:利用等价性证明