轴对称2[上学期]
图片预览




文档简介
课件26张PPT。§14.1 轴对称(第二课时)
线段的垂直平分线轴
对
称
图
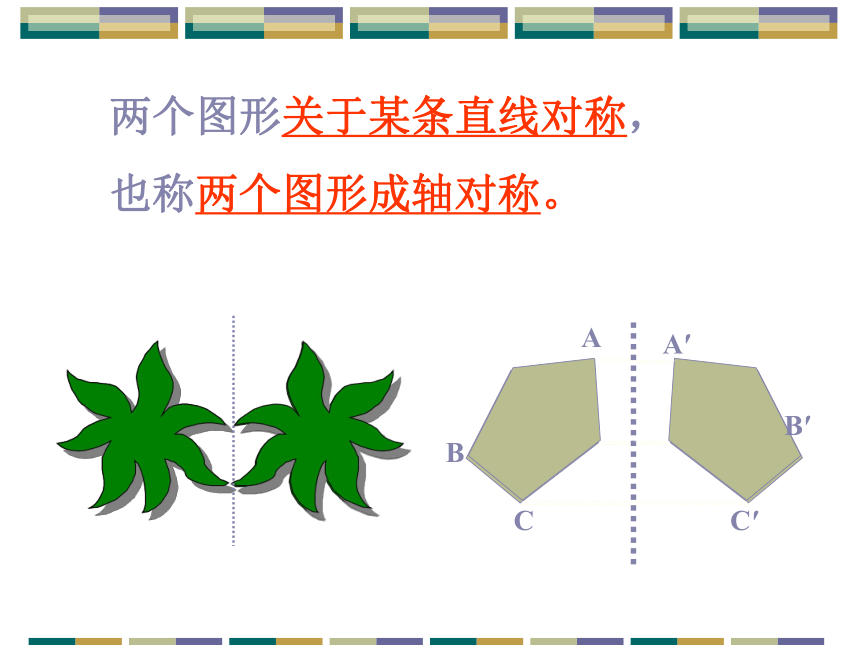
形车标设计本田丰田大众奥迪三菱奔驰一汽神龙富康A′ABCB′C′ 两个图形关于某条直线对称,
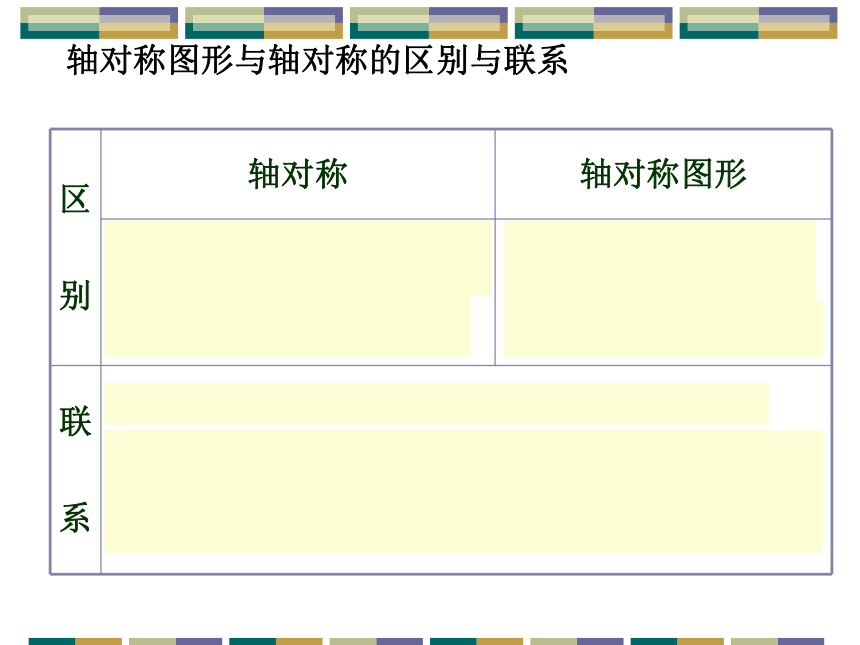
也称两个图形成轴对称。轴对称图形与轴对称的区别与联系实验探究1..折一折:
2.说一说:
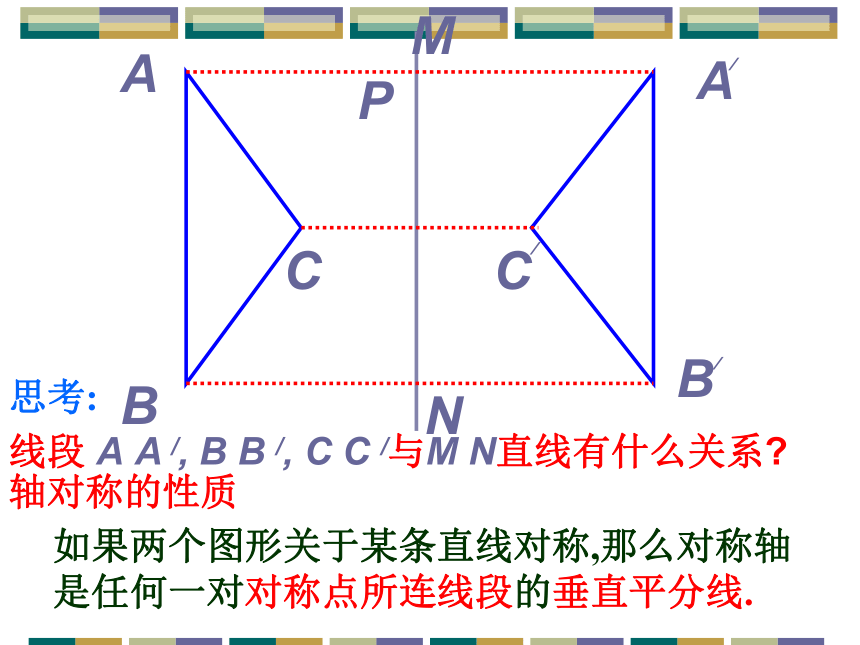
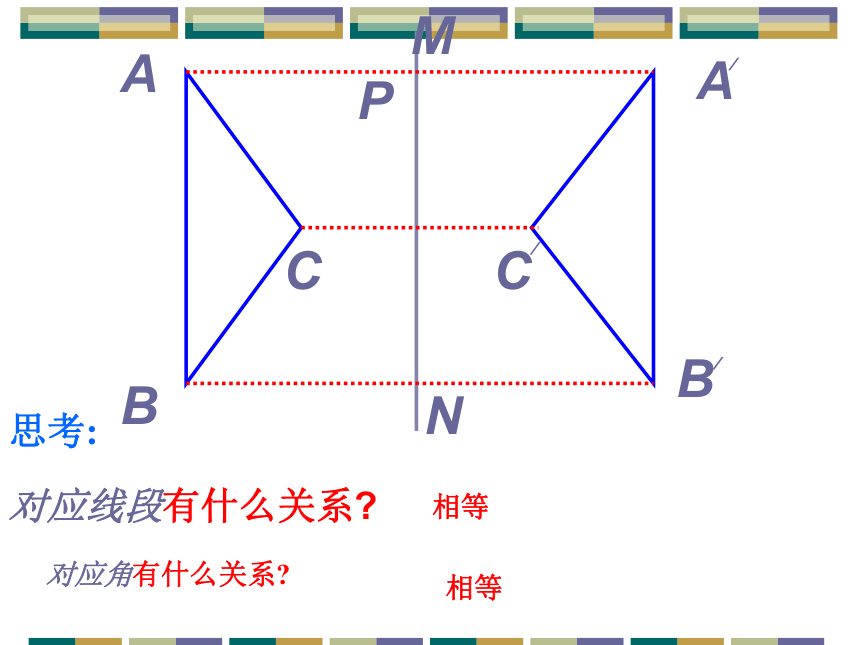
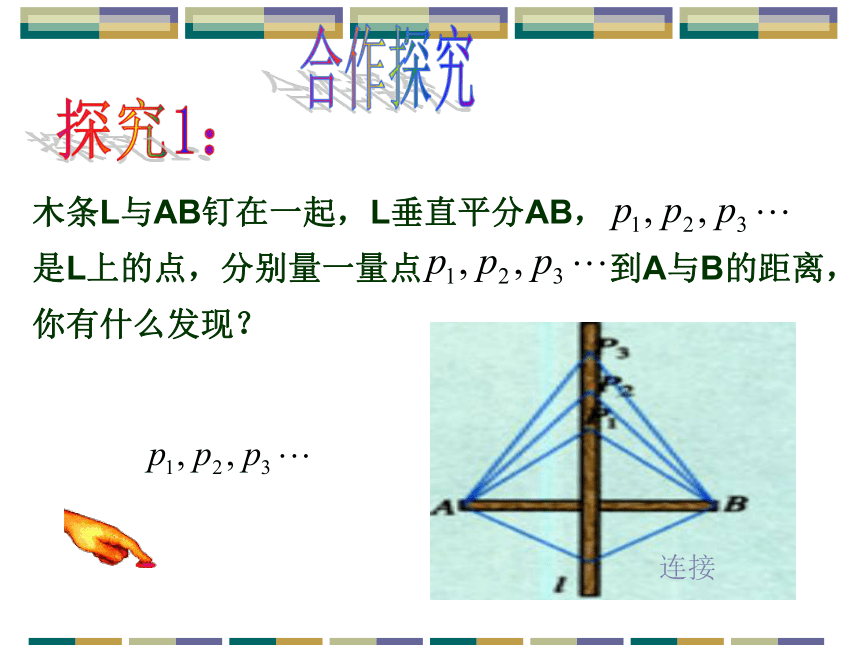
观察图形,线段AB与m的位置关系?p轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线.轴对称图形的性质ABA CBCPMN线段 A A /, B B /, C C /与M N直线有什么关系?///思考:轴对称的性质如果两个图形关于某条直线对称,那么对称轴是任何一对对称点所连线段的垂直平分线.ABA CBCPMN对应线段有什么关系?///思考:对应角有什么关系?相等相等连接木条L与AB钉在一起,L垂直平分AB, 是L上的点,分别量一量点 到A与B的距离,你有什么发现? 合作探究探究1:命题:线段垂直平分线上的点和这条线段两个 端点的距离相等。CC点P在线段AB的垂直平分线上PA=PB∵ ∴
∵AC=BC,MN⊥AB,P是MN上任意一点
∴PA=PB
( ).线段垂直平分线上的点
与这条线段两个端点距离相等www.czsx.com.cn拓展:如图所示,在△ABC中,AB=AC=32,MN是AB的垂直平分线,且有BC=21,求△BCN的周长。∵MN是AB的垂直平分线
∴AN=BN∴△BCN的周长=
BC+BN+CN=BC+AN+CN
=AC+BC=32+21=53C性质:线段垂直平分线上的点和这条线段两个端 点的距离相等。 思考: 和一条线段两个端点距离相等的点,是否一定在这条线段的垂直平分线上。垂直平分线判定:和一条线段两个端点距离相等的点,
在这条线段的垂直平分线上。已知:PA=PB
求证:点P在AB的垂直平分线上证:在过P点作AB的垂线段PC,垂足为C在Rt△ACP和Rt△BCP中PC=PCPA=PB∴Rt△ACP≌Rt△BCP∴AC=BC又∵PC⊥AB点P在AB的垂直平分线上判定:和一条线段两个端点距离相等的点,在这条线段的垂直平分线上。性质:线段垂直平分线上的点和这条线段两个端点的距离相等。三、 线段的垂直平分线的集合定义:
线段的垂直平分线可以看作是和线段 两个端点距离相等的所有点的集合用一根木棒和一根弹性均匀的橡皮筋,做一 个简易的“弓”,“箭”通过木棒中央的孔射出去,怎样才能保持射出去的方向与木棒垂直呢?为什么
CBA只要AB=BC就可以ACB∵AC=BC,MA=MB∴C,M都在线段AB的
垂直平分线上根据:两点确定一条直线M∴直线CM就是AB的
垂直平分线平分线三、 线段的垂直平分线的集合定义:
线段的垂直平分线可以看作是和线段两个端点距离相等的所有点的集合例1 已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P.
求证:PA=PB=PC;证∵点P在线段AB的垂直平分线上∴PA=PB∵点P在线段BC的垂直平分线上∴PB=PC∴PA=PB=PC你能依据例1得到什么结论?结论: 三角形三边垂直平分线交于一点,
这一点到三角形三个顶点的距离相等。 椒江区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等。ABC实际问题1求作一点P,使它和已知△ABC的三个顶点距离相等.小结:一、性质:线段垂直平分线上的点
和这条线段两个端点的距离相等。二、判定:和一条线段两个端点距离
相等的点,在这条线段的垂直平分线上。三、线段的垂直平分线的集合定义:
线段的垂直平分线可以看作是和线段两个端点距离相等的所有点的集合在角的平分线上的点到这个角的两边的距离相等。到一个角的两边的距离相等的点,在这个角的平分线上。 角的平分线是到角的两边距离相等的所有点的集合线段的垂直平分线线段垂直平分线上的点和这条线段两个端点的距离相等。和一条线段两个端点距离相等的点,在这条线段的垂直平分线上。 线段的垂直平分线可以看作是和线段两上端点距离相等的所有点的集合ABMNP点的集合是一条射线点的集合是一条直线上 三 高 速 公 路ABL实际问题2 在某高速公路L的同侧,有两个化工厂A、B,为了便于两厂的工人看病,市政府计划在公路边上修建一所医院,使得两个工厂的工人都没意见,问医院的院址应选在何处?运
用
新
知2、如图,在直线L上求作一点P,使PA=PB.数学问题源于生活实践,反过来数学又为生活实践服务实际问题2京 石 高 速 公 路AL实际问题2的变形 运用新知:在某高速公路L的同侧,有两个化工厂A、B,市政府计划在公路边上修建一所医院,问医院的院址应选在何处使总路程最短?BA’C3.如图,在L上找一点,使AC+CB
是最小值。数学问题源于生活实践,反过来数学又为生活实践服务这节课你学会了什么?你有什么新的收获?ABA CBCPMN线段 A A /, B B /, C C /与M N直线有什么关系?///思考:
线段的垂直平分线轴
对
称
图
形车标设计本田丰田大众奥迪三菱奔驰一汽神龙富康A′ABCB′C′ 两个图形关于某条直线对称,
也称两个图形成轴对称。轴对称图形与轴对称的区别与联系实验探究1..折一折:
2.说一说:
观察图形,线段AB与m的位置关系?p轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线.轴对称图形的性质ABA CBCPMN线段 A A /, B B /, C C /与M N直线有什么关系?///思考:轴对称的性质如果两个图形关于某条直线对称,那么对称轴是任何一对对称点所连线段的垂直平分线.ABA CBCPMN对应线段有什么关系?///思考:对应角有什么关系?相等相等连接木条L与AB钉在一起,L垂直平分AB, 是L上的点,分别量一量点 到A与B的距离,你有什么发现? 合作探究探究1:命题:线段垂直平分线上的点和这条线段两个 端点的距离相等。CC点P在线段AB的垂直平分线上PA=PB∵ ∴
∵AC=BC,MN⊥AB,P是MN上任意一点
∴PA=PB
( ).线段垂直平分线上的点
与这条线段两个端点距离相等www.czsx.com.cn拓展:如图所示,在△ABC中,AB=AC=32,MN是AB的垂直平分线,且有BC=21,求△BCN的周长。∵MN是AB的垂直平分线
∴AN=BN∴△BCN的周长=
BC+BN+CN=BC+AN+CN
=AC+BC=32+21=53C性质:线段垂直平分线上的点和这条线段两个端 点的距离相等。 思考: 和一条线段两个端点距离相等的点,是否一定在这条线段的垂直平分线上。垂直平分线判定:和一条线段两个端点距离相等的点,
在这条线段的垂直平分线上。已知:PA=PB
求证:点P在AB的垂直平分线上证:在过P点作AB的垂线段PC,垂足为C在Rt△ACP和Rt△BCP中PC=PCPA=PB∴Rt△ACP≌Rt△BCP∴AC=BC又∵PC⊥AB点P在AB的垂直平分线上判定:和一条线段两个端点距离相等的点,在这条线段的垂直平分线上。性质:线段垂直平分线上的点和这条线段两个端点的距离相等。三、 线段的垂直平分线的集合定义:
线段的垂直平分线可以看作是和线段 两个端点距离相等的所有点的集合用一根木棒和一根弹性均匀的橡皮筋,做一 个简易的“弓”,“箭”通过木棒中央的孔射出去,怎样才能保持射出去的方向与木棒垂直呢?为什么
CBA只要AB=BC就可以ACB∵AC=BC,MA=MB∴C,M都在线段AB的
垂直平分线上根据:两点确定一条直线M∴直线CM就是AB的
垂直平分线平分线三、 线段的垂直平分线的集合定义:
线段的垂直平分线可以看作是和线段两个端点距离相等的所有点的集合例1 已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P.
求证:PA=PB=PC;证∵点P在线段AB的垂直平分线上∴PA=PB∵点P在线段BC的垂直平分线上∴PB=PC∴PA=PB=PC你能依据例1得到什么结论?结论: 三角形三边垂直平分线交于一点,
这一点到三角形三个顶点的距离相等。 椒江区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等。ABC实际问题1求作一点P,使它和已知△ABC的三个顶点距离相等.小结:一、性质:线段垂直平分线上的点
和这条线段两个端点的距离相等。二、判定:和一条线段两个端点距离
相等的点,在这条线段的垂直平分线上。三、线段的垂直平分线的集合定义:
线段的垂直平分线可以看作是和线段两个端点距离相等的所有点的集合在角的平分线上的点到这个角的两边的距离相等。到一个角的两边的距离相等的点,在这个角的平分线上。 角的平分线是到角的两边距离相等的所有点的集合线段的垂直平分线线段垂直平分线上的点和这条线段两个端点的距离相等。和一条线段两个端点距离相等的点,在这条线段的垂直平分线上。 线段的垂直平分线可以看作是和线段两上端点距离相等的所有点的集合ABMNP点的集合是一条射线点的集合是一条直线上 三 高 速 公 路ABL实际问题2 在某高速公路L的同侧,有两个化工厂A、B,为了便于两厂的工人看病,市政府计划在公路边上修建一所医院,使得两个工厂的工人都没意见,问医院的院址应选在何处?运
用
新
知2、如图,在直线L上求作一点P,使PA=PB.数学问题源于生活实践,反过来数学又为生活实践服务实际问题2京 石 高 速 公 路AL实际问题2的变形 运用新知:在某高速公路L的同侧,有两个化工厂A、B,市政府计划在公路边上修建一所医院,问医院的院址应选在何处使总路程最短?BA’C3.如图,在L上找一点,使AC+CB
是最小值。数学问题源于生活实践,反过来数学又为生活实践服务这节课你学会了什么?你有什么新的收获?ABA CBCPMN线段 A A /, B B /, C C /与M N直线有什么关系?///思考:
