华师大版九年级数学上册 第23章图形的相似 单元测试(含解析)
文档属性
| 名称 | 华师大版九年级数学上册 第23章图形的相似 单元测试(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-19 18:56:46 | ||
图片预览

文档简介
华师大版九年级数学上册单元测试
第23章图形的相似
一、选择题(每题3分,共24分)
1.已知三条线段的长分别为3,4,6,则下列线段中不能与它们组成比例线段的是 ( )
A.2 B.4.5 C.5 D.8
2.若,,则的值为 ( )
A.1 B.2 C.3 D.4
3.如图,直线a∥b∥c,直线AC分别交a,b,c于点A,B,C,直线DF分别交a,b,c于点D,E,F.若DE=2EF,AC=6,则AB的长为 ( )
A.2 B.3 C.4 D.5
4.如图,测量小玻璃管口径的量具ABC上,AB的长为10毫米,AC被分为60等份,如果小管口中DE正好对着量具上20份处(DEAB),那么小管口径DE的长度是 ( )
A.5毫米 B.毫米 C.毫米 D.2毫米
5.如图,已知点G是△ABC的重心,分别延长线段BG、CG,交边AC、AB于点E,D.若BE=15,则BG的长是 ( )
A.5 B.7.5 C.9 D.10
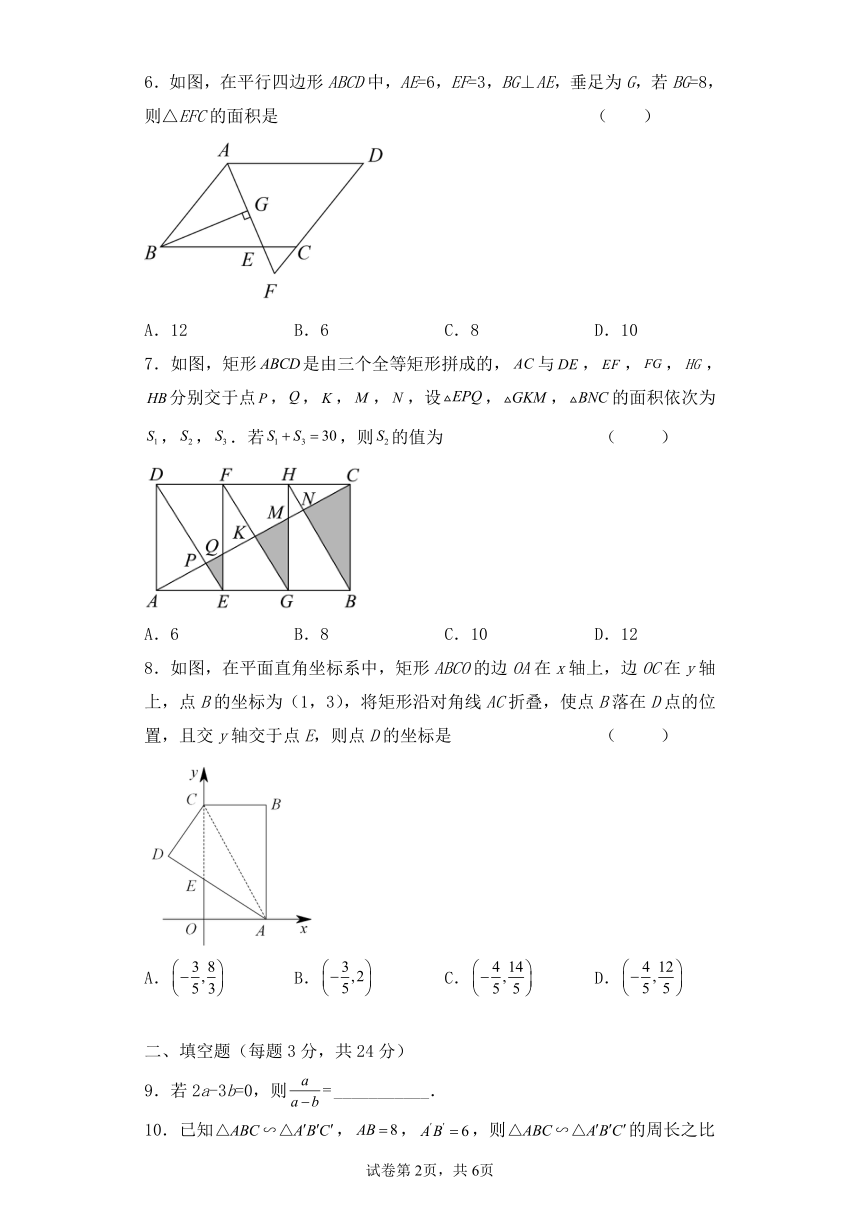
6.如图,在平行四边形ABCD中,AE=6,EF=3,BG⊥AE,垂足为G,若BG=8,则△EFC的面积是 ( )
A.12 B.6 C.8 D.10
7.如图,矩形是由三个全等矩形拼成的,与,,,,分别交于点,,,,,设,,的面积依次为,,.若,则的值为 ( )
A.6 B.8 C.10 D.12
8.如图,在平面直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC折叠,使点B落在D点的位置,且交y轴交于点E,则点D的坐标是 ( )
A. B. C. D.
二、填空题(每题3分,共24分)
9.若2a-3b=0,则___________.
10.已知,,,则的周长之比为____.
11.若a=4cm,b=9cm,则线段a,b的比例中项是______cm.
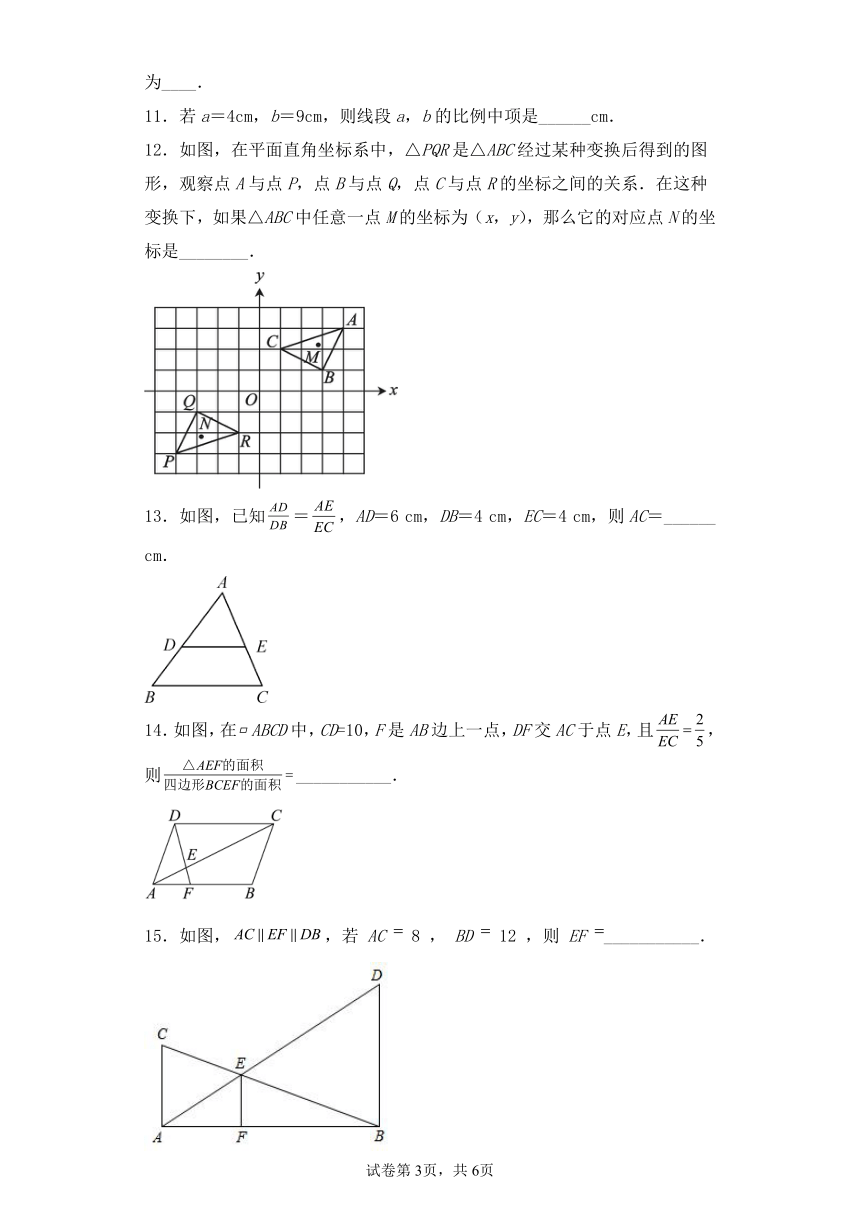
12.如图,在平面直角坐标系中,△PQR是△ABC经过某种变换后得到的图形,观察点A与点P,点B与点Q,点C与点R的坐标之间的关系.在这种变换下,如果△ABC中任意一点M的坐标为(x,y),那么它的对应点N的坐标是________.
13.如图,已知=,AD=6 cm,DB=4 cm,EC=4 cm,则AC=______ cm.
14.如图,在ABCD中,CD=10,F是AB边上一点,DF交AC于点E,且,则___________.
15.如图,,若 AC 8 , BD 12 ,则 EF ___________.
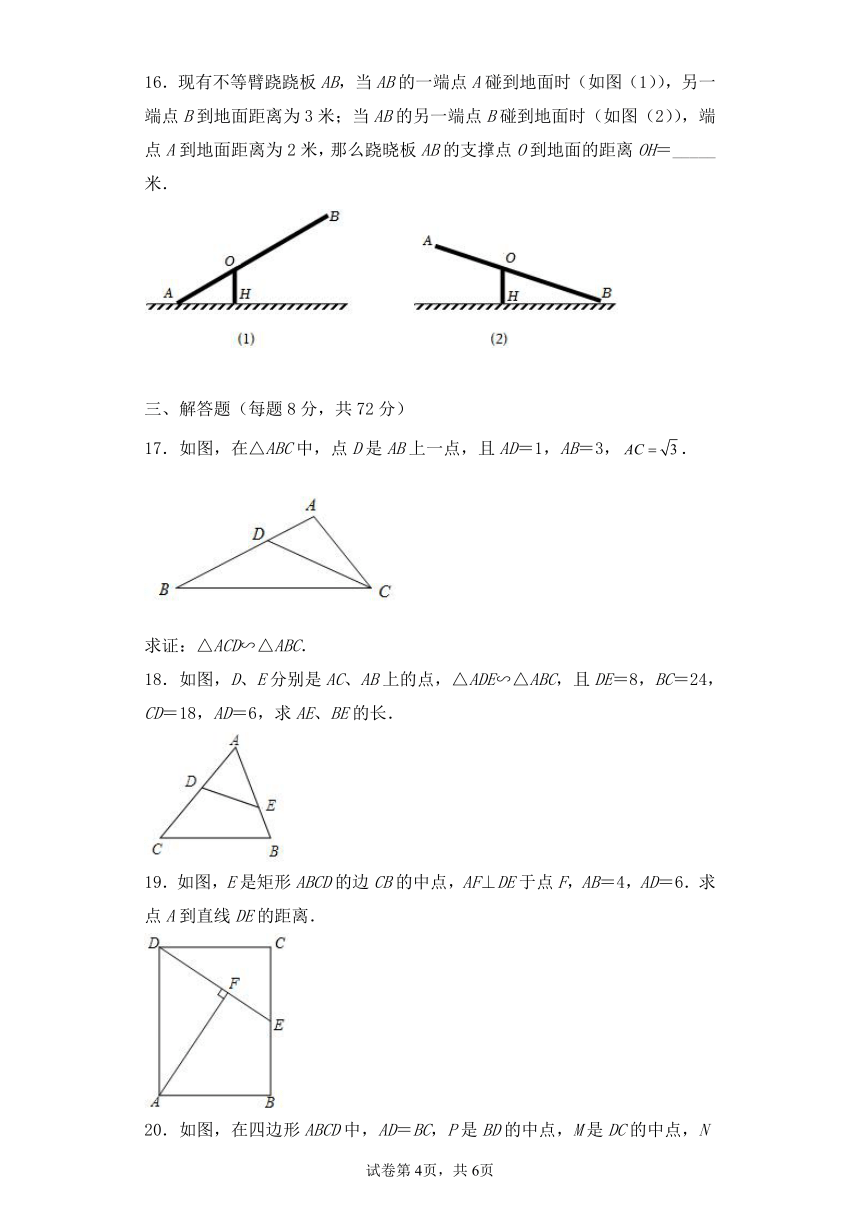
16.现有不等臂跷跷板AB,当AB的一端点A碰到地面时(如图(1)),另一端点B到地面距离为3米;当AB的另一端点B碰到地面时(如图(2)),端点A到地面距离为2米,那么跷晓板AB的支撑点O到地面的距离OH=_____米.
三、解答题(每题8分,共72分)
17.如图,在△ABC中,点D是AB上一点,且AD=1,AB=3,.
求证:△ACD∽△ABC.
18.如图,D、E分别是AC、AB上的点,△ADE∽△ABC,且DE=8,BC=24,CD=18,AD=6,求AE、BE的长.
19.如图,E是矩形ABCD的边CB的中点,AF⊥DE于点F,AB=4,AD=6.求点A到直线DE的距离.
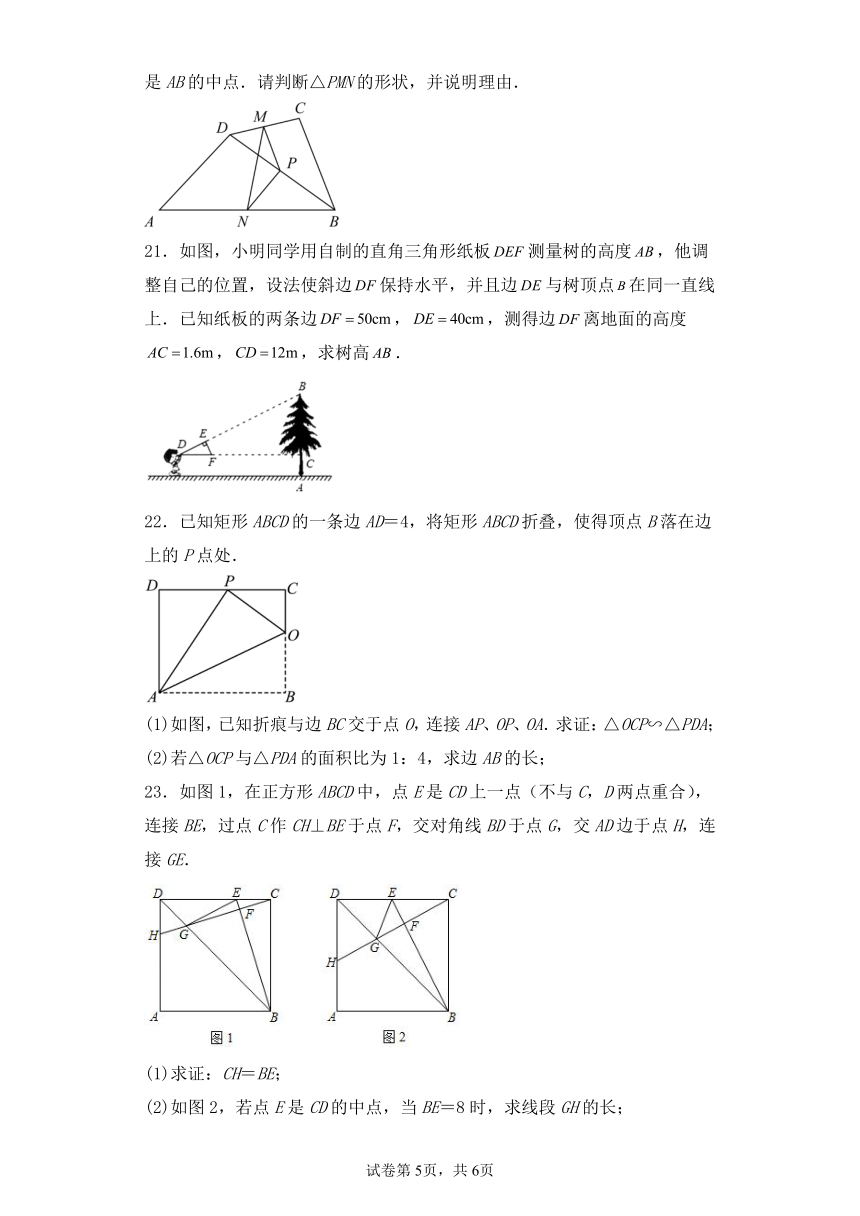
20.如图,在四边形ABCD中,AD=BC,P是BD的中点,M是DC的中点,N是AB的中点.请判断△PMN的形状,并说明理由.
21.如图,小明同学用自制的直角三角形纸板测量树的高度,他调整自己的位置,设法使斜边保持水平,并且边与树顶点在同一直线上.已知纸板的两条边,,测得边离地面的高度,,求树高.
22.已知矩形ABCD的一条边AD=4,将矩形ABCD折叠,使得顶点B落在边上的P点处.
(1)如图,已知折痕与边BC交于点O,连接AP、OP、OA.求证:△OCP∽△PDA;
(2)若△OCP与△PDA的面积比为1:4,求边AB的长;
23.如图1,在正方形ABCD中,点E是CD上一点(不与C,D两点重合),连接BE,过点C作CH⊥BE于点F,交对角线BD于点G,交AD边于点H,连接GE.
(1)求证:CH=BE;
(2)如图2,若点E是CD的中点,当BE=8时,求线段GH的长;
(3)设正方形ABCD的面积为S1,四边形DEGH的面积为S2,当的值为时,求的值.
24.在△ABC中,AC>BC,D为AB的中点,E为线段AC上的一点.
(1)如图1,若AE=AC,∠C=90°,BC=2,AC=4,求DE的长;
(2)如图2,若AE=BC且F为EC中点,求证:∠AFD=∠C;
(3)若2∠AED-∠C=180°,试探究AE、BC、AC的数量关系,并证明.
25.已知在Rt△ABC中,∠BAC=90°,AB=2,AC=6,D为BC边上的一点.过点D作射线DE⊥DF,分别交边AB,AC于点E,F.
(1)当D为BC的中点,且DE⊥AB,DF⊥AC时,如图①,______.
(2)①若D为BC的中点,将∠EDF绕点D旋转到图②位置时,______.
②若改变点D的位置,且时,求的值,请就图③的情形写出解答过程.
(3)如图③连接EF,当BD=______时,△DEF与△ABC相似.
试卷第2页,共2页
试卷第2页,共6页
参考答案:
1.
解:A、∵2×6=3×4,∴四条线段能组成比例线段,故选项不符合题意;
B、∵3×6=4×4.5,∴四条线段能组成比例线段,故选项不符合题意;
C、∵3×6≠4×5,∴四条线段不能组成比例线段,故选项符合题意;
D、∵3×8=4×6,∴四条线段能组成比例线段,故选项不符合题意.
故选:C.
2.
解:设,则,,,
,即,
,
,
故选:D.
3.
解:∵abc,
∴=,
∵DE=2EF,AC=6,
∴=2,
解得:AB=4,
故选:C.
4.
∵DEAB,
∴△CDE∽△CAB,
∴,即,
解得:DE=,
故选B.
5.
解:∵点G是△ABC的重心,
∴BG=2GE,
∵BE=BG+GE=15,
∴BG=10,
故选:D.
6.
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠F=∠BAE,
∵∠FEC=∠AEB,
∴△EFC∽△EAB,
∴;
∵BG⊥AE,BG=8,
∴,
∴,
故选:B.
7.
解:∵矩形ABCD是由三个全等矩形拼成,
∴,
∴∠AED=∠EGF=∠GBH,
∴∠DEF=∠FGH=∠HBC,
∵FEHGBC,
∴∠AQE=∠AMG=∠ACB,
∴△EPQ∽△GKM∽△BNC,
∵QEMG,
∴△AEQ∽△AGM,
∴
∵MGCB,
∴△AGM∽△ABC,
∴则
∵
∴
∴,
故选D.
8.
解:如图,过D作DF⊥AO于F,
∵点B的坐标为(1,3),
∴AO=1,AB=3,
根据折叠可知:CD=OA,
而∠D=∠AOE=90°,∠DEC=∠AEO,
∴,
∴OE=DE,OA=CD=1,
设OE=m,那么CE=3-m,DE=m,
∴在Rt△DCE中,,
∴,
解得,
∵DF⊥AF,
∴,
∴,
而AD=AB=3,
∴,
∴,
即,
∴,
∴,
∴D的坐标为.
故选:D.
9.
解:∵2a-3b=0,
∴2a=3b,即,
∴.
故答案为:3
10.
解:∵,,,
∴;
故答案为:4∶3.
11.
解:设线段a,b的比例中项是xcm,
∵a=4cm,b=9cm,
∴,
∴x=6cm.
故答案为:6
12.
解:观察图形可知C(1,2)、P(﹣4,﹣3)、Q(﹣3,﹣1)、A(4,3)、B(3,1)、R(﹣1,﹣2),
∴C、R关于原点对称,A、P关于原点对称,B、Q关于原点对称,
∴△PQR和△ABC关于原点对称.
∵△PQR和△ABC关于原点对称, M(x,y)与N对称点,
∴N点坐标为:(﹣x,﹣y).
故答案为:(﹣x,﹣y).
13.
解:∵=,且AD=6 cm,DB=4 cm,EC=4 cm,
∴=,
∴AE=6cm,
∴AC=AE+EC=6+4=10cm,
故答案为:10.
14.
解:如图所示,平行四边形,过点作交于点,交于点,,,
∴,
∴,,,
∴,
∴,
∴,,
∴,则,
∵,,
∴,
∴,
故答案是:.
15.
解:∵,
∴△BEF∽△BCA,
∴,
∵,
∴△AEF∽△ADB,
∴,
∴,
即,
∴,
∵AC 8 , BD 12 ,
∴,
解得:.
故答案为:
16.
解:如图所示:过点B作BN⊥AH于点N,AM⊥BH于点M,
∴,
∴,,
∴△AOH∽△ABN,
∴,
即①,
同理可得:△BOH∽△BAM,
∴,
即②,
①+②,得,
∴OH=1.2(米),
故答案为:1.2.
17.
证明:AD=1,AB=3,AC=
,
又
∽
18.
解:∵△ADE∽△ABC,
∴,
∵DE=8,BC=24,CD=18,AD=6,
∴AC=AD+CD=24,
∴AE=8,AB=18,
∴BE=AB-AE=10.
19.
解:∵四边形ABCD是矩形,
∴AD=BC=6,CD=AB=4,∠ADC=∠C=90°,
∵点E为BC的中点,
∴CE=3,
由勾股定理得,,
∵AF⊥DE,
∴∠AFD=90°,
∴∠ADF+∠DAF=∠ADF+∠CDE=90°,
∴∠DAF=∠CDE,
∵∠DFA=∠C,
∴,
∴,
∴,
∴AF=,
即点A到直线DE的距离为.
20.
解:△PMN是等腰三角形,
理由如下:∵P是BD的中点,M是DC的中点,
∴PM是△DBC的中位线,
∴PM=BC,
同理,PN=AD,
∵AD=BC,
∴PM=PN,
∴△PMN是等腰三角形.
21.
解:在中, ,,
由勾股定理得:,
∴,
根据题意得:∠BCD=∠DEF=90°,∠D=∠D,
∴,
∴,
∵,,
∴,解得:,
∵,
∴.
22.
(1)∵四边形ABCD是矩形,
∴.
由折叠的性质可知,
∴,
∴,
∴,
∴△PDA∽△OCP;
(2)∵,△PDA∽△OCP,
∴,即,
∴.
设,则,
由折叠可知,
∵,
∴,
解得:,
∴,
∴,
∴,
∴.
23.
(1)解:∵四边形ABCD是正方形,
∴CD=BC,∠HDC=∠BCE=90°,
∴∠DHC+∠DCH=90°,
∵CH⊥BE,
∴∠EFC=90°,
∴∠ECF+∠BEC=90°,
∴∠CHD=∠BEC,
∴△DHC≌△CEB(AAS),
∴CH=BE;
(2)解:∵△DHC≌△CEB,
∴CH=BE,DH=CE,
∵CE=DE=CD,CD=CB,
∴DH=BC,
∵DHBC,
∴,
∴GC=2GH,
设GH=x,则CG=2x,
∴3x=8,
∴x=.
即GH=;
(3)解:当的值为时,则,
∵DH=CE,DC=BC,
,
∵DHBC,
,
,
设S△DGH=9a,则S△BCG=49a,S△DCG=21a,
∴S△BCD=49a+21a=70a,
∴S1=2S△BCD=140a,
∵S△DEG:S△CEG=4:3,
∴S△DEG=12a,
∴S2=12a+9a=21a.
∴.
24.
(1)证明:取AC的中点G,连接DG,(如图1)
∵D为AB的中点,
∴DG为△ACB的中位线,
∴DG=BC=1,DGBC,
∵∠C=90°,
∴DG⊥BC,
∵AE=AC,AC=4,
∴AE=1,
在Rt△DGE中,DE=;
(2)证明:连接BE,取BE中点M,再连接MF、MD.(如图2)
∵F为EC中点,D为AB中点,
∴MFBC且MF=BC,MDAB且MD=AE,
∴MF=MD,
∴∠MDF=∠MFD,
又∵MDAE,
∴∠AFD=∠MDF,
∴∠AFD=∠AFM,
∵MFAC,
∴∠AFM=∠ACB,
∴∠AFD=∠ACB,
即:∠AFD=∠C;
(3)解:AC=2AE+BC,(如图3)
证明:在EC上截取EM=AE,连接BM,作CH⊥BM,
∵AE=EM,AD=DB,
∴DEBM,
∴∠AED=∠AMB=∠MHC+∠MCH=90°+∠MCH,
∵2∠AED-∠ACB =180°,
∴∠AED=90°+∠ACB,
∴∠MCH=∠ACB,
∴∠ACB =2∠MCH,
∴△CHM≌△CHB,
∴BC=MC,
∴AC=2AE+BC.
25.
(1)解:,,,
,,
点是的中点,
、是的中位线,
,,
,
故答案为:3;
(2)①过点作于点,于点,如图2所示:
则,
四边形是矩形,
,即,
,
,即,
,
,
,
同(1)得:,
,
故答案为:3;
②过点作于点,于点,如图3所示:
,
四边形是矩形,
,,,,
,
,,
,,
,,
,,
,,
与①同理得:,
;
(3)如图所示:
在中,由勾股定理得:,
,
与相似分两种情况:
①,则,即,整理得:,
,
;
②,则,即,整理得:,
,
;
综上所述,当或时,与相似;
故答案为:或.
答案第1页,共2页
第23章图形的相似
一、选择题(每题3分,共24分)
1.已知三条线段的长分别为3,4,6,则下列线段中不能与它们组成比例线段的是 ( )
A.2 B.4.5 C.5 D.8
2.若,,则的值为 ( )
A.1 B.2 C.3 D.4
3.如图,直线a∥b∥c,直线AC分别交a,b,c于点A,B,C,直线DF分别交a,b,c于点D,E,F.若DE=2EF,AC=6,则AB的长为 ( )
A.2 B.3 C.4 D.5
4.如图,测量小玻璃管口径的量具ABC上,AB的长为10毫米,AC被分为60等份,如果小管口中DE正好对着量具上20份处(DEAB),那么小管口径DE的长度是 ( )
A.5毫米 B.毫米 C.毫米 D.2毫米
5.如图,已知点G是△ABC的重心,分别延长线段BG、CG,交边AC、AB于点E,D.若BE=15,则BG的长是 ( )
A.5 B.7.5 C.9 D.10
6.如图,在平行四边形ABCD中,AE=6,EF=3,BG⊥AE,垂足为G,若BG=8,则△EFC的面积是 ( )
A.12 B.6 C.8 D.10
7.如图,矩形是由三个全等矩形拼成的,与,,,,分别交于点,,,,,设,,的面积依次为,,.若,则的值为 ( )
A.6 B.8 C.10 D.12
8.如图,在平面直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC折叠,使点B落在D点的位置,且交y轴交于点E,则点D的坐标是 ( )
A. B. C. D.
二、填空题(每题3分,共24分)
9.若2a-3b=0,则___________.
10.已知,,,则的周长之比为____.
11.若a=4cm,b=9cm,则线段a,b的比例中项是______cm.
12.如图,在平面直角坐标系中,△PQR是△ABC经过某种变换后得到的图形,观察点A与点P,点B与点Q,点C与点R的坐标之间的关系.在这种变换下,如果△ABC中任意一点M的坐标为(x,y),那么它的对应点N的坐标是________.
13.如图,已知=,AD=6 cm,DB=4 cm,EC=4 cm,则AC=______ cm.
14.如图,在ABCD中,CD=10,F是AB边上一点,DF交AC于点E,且,则___________.
15.如图,,若 AC 8 , BD 12 ,则 EF ___________.
16.现有不等臂跷跷板AB,当AB的一端点A碰到地面时(如图(1)),另一端点B到地面距离为3米;当AB的另一端点B碰到地面时(如图(2)),端点A到地面距离为2米,那么跷晓板AB的支撑点O到地面的距离OH=_____米.
三、解答题(每题8分,共72分)
17.如图,在△ABC中,点D是AB上一点,且AD=1,AB=3,.
求证:△ACD∽△ABC.
18.如图,D、E分别是AC、AB上的点,△ADE∽△ABC,且DE=8,BC=24,CD=18,AD=6,求AE、BE的长.
19.如图,E是矩形ABCD的边CB的中点,AF⊥DE于点F,AB=4,AD=6.求点A到直线DE的距离.
20.如图,在四边形ABCD中,AD=BC,P是BD的中点,M是DC的中点,N是AB的中点.请判断△PMN的形状,并说明理由.
21.如图,小明同学用自制的直角三角形纸板测量树的高度,他调整自己的位置,设法使斜边保持水平,并且边与树顶点在同一直线上.已知纸板的两条边,,测得边离地面的高度,,求树高.
22.已知矩形ABCD的一条边AD=4,将矩形ABCD折叠,使得顶点B落在边上的P点处.
(1)如图,已知折痕与边BC交于点O,连接AP、OP、OA.求证:△OCP∽△PDA;
(2)若△OCP与△PDA的面积比为1:4,求边AB的长;
23.如图1,在正方形ABCD中,点E是CD上一点(不与C,D两点重合),连接BE,过点C作CH⊥BE于点F,交对角线BD于点G,交AD边于点H,连接GE.
(1)求证:CH=BE;
(2)如图2,若点E是CD的中点,当BE=8时,求线段GH的长;
(3)设正方形ABCD的面积为S1,四边形DEGH的面积为S2,当的值为时,求的值.
24.在△ABC中,AC>BC,D为AB的中点,E为线段AC上的一点.
(1)如图1,若AE=AC,∠C=90°,BC=2,AC=4,求DE的长;
(2)如图2,若AE=BC且F为EC中点,求证:∠AFD=∠C;
(3)若2∠AED-∠C=180°,试探究AE、BC、AC的数量关系,并证明.
25.已知在Rt△ABC中,∠BAC=90°,AB=2,AC=6,D为BC边上的一点.过点D作射线DE⊥DF,分别交边AB,AC于点E,F.
(1)当D为BC的中点,且DE⊥AB,DF⊥AC时,如图①,______.
(2)①若D为BC的中点,将∠EDF绕点D旋转到图②位置时,______.
②若改变点D的位置,且时,求的值,请就图③的情形写出解答过程.
(3)如图③连接EF,当BD=______时,△DEF与△ABC相似.
试卷第2页,共2页
试卷第2页,共6页
参考答案:
1.
解:A、∵2×6=3×4,∴四条线段能组成比例线段,故选项不符合题意;
B、∵3×6=4×4.5,∴四条线段能组成比例线段,故选项不符合题意;
C、∵3×6≠4×5,∴四条线段不能组成比例线段,故选项符合题意;
D、∵3×8=4×6,∴四条线段能组成比例线段,故选项不符合题意.
故选:C.
2.
解:设,则,,,
,即,
,
,
故选:D.
3.
解:∵abc,
∴=,
∵DE=2EF,AC=6,
∴=2,
解得:AB=4,
故选:C.
4.
∵DEAB,
∴△CDE∽△CAB,
∴,即,
解得:DE=,
故选B.
5.
解:∵点G是△ABC的重心,
∴BG=2GE,
∵BE=BG+GE=15,
∴BG=10,
故选:D.
6.
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠F=∠BAE,
∵∠FEC=∠AEB,
∴△EFC∽△EAB,
∴;
∵BG⊥AE,BG=8,
∴,
∴,
故选:B.
7.
解:∵矩形ABCD是由三个全等矩形拼成,
∴,
∴∠AED=∠EGF=∠GBH,
∴∠DEF=∠FGH=∠HBC,
∵FEHGBC,
∴∠AQE=∠AMG=∠ACB,
∴△EPQ∽△GKM∽△BNC,
∵QEMG,
∴△AEQ∽△AGM,
∴
∵MGCB,
∴△AGM∽△ABC,
∴则
∵
∴
∴,
故选D.
8.
解:如图,过D作DF⊥AO于F,
∵点B的坐标为(1,3),
∴AO=1,AB=3,
根据折叠可知:CD=OA,
而∠D=∠AOE=90°,∠DEC=∠AEO,
∴,
∴OE=DE,OA=CD=1,
设OE=m,那么CE=3-m,DE=m,
∴在Rt△DCE中,,
∴,
解得,
∵DF⊥AF,
∴,
∴,
而AD=AB=3,
∴,
∴,
即,
∴,
∴,
∴D的坐标为.
故选:D.
9.
解:∵2a-3b=0,
∴2a=3b,即,
∴.
故答案为:3
10.
解:∵,,,
∴;
故答案为:4∶3.
11.
解:设线段a,b的比例中项是xcm,
∵a=4cm,b=9cm,
∴,
∴x=6cm.
故答案为:6
12.
解:观察图形可知C(1,2)、P(﹣4,﹣3)、Q(﹣3,﹣1)、A(4,3)、B(3,1)、R(﹣1,﹣2),
∴C、R关于原点对称,A、P关于原点对称,B、Q关于原点对称,
∴△PQR和△ABC关于原点对称.
∵△PQR和△ABC关于原点对称, M(x,y)与N对称点,
∴N点坐标为:(﹣x,﹣y).
故答案为:(﹣x,﹣y).
13.
解:∵=,且AD=6 cm,DB=4 cm,EC=4 cm,
∴=,
∴AE=6cm,
∴AC=AE+EC=6+4=10cm,
故答案为:10.
14.
解:如图所示,平行四边形,过点作交于点,交于点,,,
∴,
∴,,,
∴,
∴,
∴,,
∴,则,
∵,,
∴,
∴,
故答案是:.
15.
解:∵,
∴△BEF∽△BCA,
∴,
∵,
∴△AEF∽△ADB,
∴,
∴,
即,
∴,
∵AC 8 , BD 12 ,
∴,
解得:.
故答案为:
16.
解:如图所示:过点B作BN⊥AH于点N,AM⊥BH于点M,
∴,
∴,,
∴△AOH∽△ABN,
∴,
即①,
同理可得:△BOH∽△BAM,
∴,
即②,
①+②,得,
∴OH=1.2(米),
故答案为:1.2.
17.
证明:AD=1,AB=3,AC=
,
又
∽
18.
解:∵△ADE∽△ABC,
∴,
∵DE=8,BC=24,CD=18,AD=6,
∴AC=AD+CD=24,
∴AE=8,AB=18,
∴BE=AB-AE=10.
19.
解:∵四边形ABCD是矩形,
∴AD=BC=6,CD=AB=4,∠ADC=∠C=90°,
∵点E为BC的中点,
∴CE=3,
由勾股定理得,,
∵AF⊥DE,
∴∠AFD=90°,
∴∠ADF+∠DAF=∠ADF+∠CDE=90°,
∴∠DAF=∠CDE,
∵∠DFA=∠C,
∴,
∴,
∴,
∴AF=,
即点A到直线DE的距离为.
20.
解:△PMN是等腰三角形,
理由如下:∵P是BD的中点,M是DC的中点,
∴PM是△DBC的中位线,
∴PM=BC,
同理,PN=AD,
∵AD=BC,
∴PM=PN,
∴△PMN是等腰三角形.
21.
解:在中, ,,
由勾股定理得:,
∴,
根据题意得:∠BCD=∠DEF=90°,∠D=∠D,
∴,
∴,
∵,,
∴,解得:,
∵,
∴.
22.
(1)∵四边形ABCD是矩形,
∴.
由折叠的性质可知,
∴,
∴,
∴,
∴△PDA∽△OCP;
(2)∵,△PDA∽△OCP,
∴,即,
∴.
设,则,
由折叠可知,
∵,
∴,
解得:,
∴,
∴,
∴,
∴.
23.
(1)解:∵四边形ABCD是正方形,
∴CD=BC,∠HDC=∠BCE=90°,
∴∠DHC+∠DCH=90°,
∵CH⊥BE,
∴∠EFC=90°,
∴∠ECF+∠BEC=90°,
∴∠CHD=∠BEC,
∴△DHC≌△CEB(AAS),
∴CH=BE;
(2)解:∵△DHC≌△CEB,
∴CH=BE,DH=CE,
∵CE=DE=CD,CD=CB,
∴DH=BC,
∵DHBC,
∴,
∴GC=2GH,
设GH=x,则CG=2x,
∴3x=8,
∴x=.
即GH=;
(3)解:当的值为时,则,
∵DH=CE,DC=BC,
,
∵DHBC,
,
,
设S△DGH=9a,则S△BCG=49a,S△DCG=21a,
∴S△BCD=49a+21a=70a,
∴S1=2S△BCD=140a,
∵S△DEG:S△CEG=4:3,
∴S△DEG=12a,
∴S2=12a+9a=21a.
∴.
24.
(1)证明:取AC的中点G,连接DG,(如图1)
∵D为AB的中点,
∴DG为△ACB的中位线,
∴DG=BC=1,DGBC,
∵∠C=90°,
∴DG⊥BC,
∵AE=AC,AC=4,
∴AE=1,
在Rt△DGE中,DE=;
(2)证明:连接BE,取BE中点M,再连接MF、MD.(如图2)
∵F为EC中点,D为AB中点,
∴MFBC且MF=BC,MDAB且MD=AE,
∴MF=MD,
∴∠MDF=∠MFD,
又∵MDAE,
∴∠AFD=∠MDF,
∴∠AFD=∠AFM,
∵MFAC,
∴∠AFM=∠ACB,
∴∠AFD=∠ACB,
即:∠AFD=∠C;
(3)解:AC=2AE+BC,(如图3)
证明:在EC上截取EM=AE,连接BM,作CH⊥BM,
∵AE=EM,AD=DB,
∴DEBM,
∴∠AED=∠AMB=∠MHC+∠MCH=90°+∠MCH,
∵2∠AED-∠ACB =180°,
∴∠AED=90°+∠ACB,
∴∠MCH=∠ACB,
∴∠ACB =2∠MCH,
∴△CHM≌△CHB,
∴BC=MC,
∴AC=2AE+BC.
25.
(1)解:,,,
,,
点是的中点,
、是的中位线,
,,
,
故答案为:3;
(2)①过点作于点,于点,如图2所示:
则,
四边形是矩形,
,即,
,
,即,
,
,
,
同(1)得:,
,
故答案为:3;
②过点作于点,于点,如图3所示:
,
四边形是矩形,
,,,,
,
,,
,,
,,
,,
,,
与①同理得:,
;
(3)如图所示:
在中,由勾股定理得:,
,
与相似分两种情况:
①,则,即,整理得:,
,
;
②,则,即,整理得:,
,
;
综上所述,当或时,与相似;
故答案为:或.
答案第1页,共2页
