轴对称[下学期]
图片预览






文档简介
课件15张PPT。课 题: 轴 对 称课 题: 轴 对 称学习目标1 理解并掌握轴对称和轴对称图形的性质。
2 了解线段垂直平分线的概念。
3 灵活掌握线段垂直平分线的性质定理及逆 定理。
能灵活运用线段垂直平分线的性质定理及 逆定理,进行简单的推理和计算。
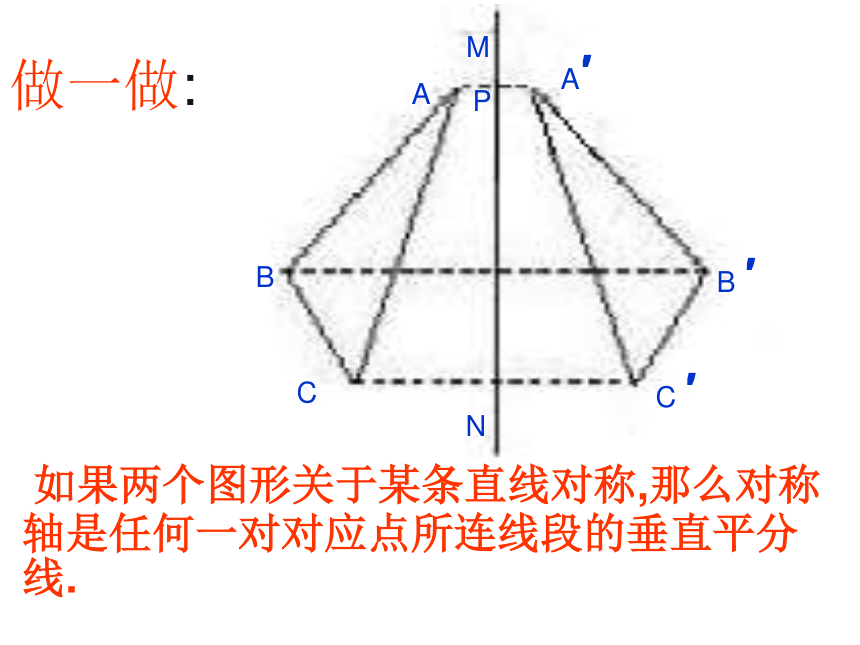
通过观察比较总结归纳猜想验证图形的性质掌握科学高效的学习方法,养成良好的学习习惯。A′ABCC ′B ′MNP做一做: 如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线. 轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线.观察与总结 如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线. 轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线.轴对称及轴对称图形的性质:如图,木条AB与L钉在一起,L垂直平分AB,P1 ,P2,P3…是L上的点,分别量一量点P1 ,P2,P3…到A与B的距离,你有什么发现?ABP1P2P3L线段垂直平分线上的点与这条线段两个端点的距离相等。如图,用一根木棒和一根弹性均匀的橡皮筋,作一个简易的“弓”,“箭”通过木棒中央的孔射出去,怎样才能保持射出去的箭的方向与木棒垂直呢?为什么?想一想:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上。例题: 如图AD⊥BC,BD=DC,点C在AE的垂直平分线上,AB、AC、CE的长度有什么关系?AB+BD与DE有什么关系?我会用!解:∵AD⊥BC,BD=DC
∴AD是BC的垂直平分线
∴AB=AC
∵点C在AE的垂直平分线上
∴AC=CE
∴ AB=AC=CE
∴ AB+BD=CE+CD=DE
即 AB+BD=DE
第一题图 第二题图 1 如图:点A和点A‘关于直线CD对称,则 __ ⊥__ , __ = __
2 如图:C是线段AB的垂直平分线上的一点,垂足为D,则下列结论中正确的有( )
①AD=BD ②AC=BC ③∠A=∠B ④∠ACD=∠BCD
⑤∠ADC=∠BDC=90°
A 2个 B 3个 C 4个 D 5个AA′ CDAO O A ′ D看看我最棒3 如图:有一块三角形田地,AB=AC=10m,作AB的垂直平分线,ED交AC于D,交AB于E,量得△BDC的周长为17m,请你帮测量人员计算BC的长.第三题图
解:∵DE垂直平分AB
∴AD=BD
∵BD+DC+BC=17
∴AD+DC+BC=17 即:AC+BC=17
又∵AC=10
∴BC=7比比谁的收获多作业:125页第3题和第5题 谢谢
2 了解线段垂直平分线的概念。
3 灵活掌握线段垂直平分线的性质定理及逆 定理。
能灵活运用线段垂直平分线的性质定理及 逆定理,进行简单的推理和计算。
通过观察比较总结归纳猜想验证图形的性质掌握科学高效的学习方法,养成良好的学习习惯。A′ABCC ′B ′MNP做一做: 如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线. 轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线.观察与总结 如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线. 轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线.轴对称及轴对称图形的性质:如图,木条AB与L钉在一起,L垂直平分AB,P1 ,P2,P3…是L上的点,分别量一量点P1 ,P2,P3…到A与B的距离,你有什么发现?ABP1P2P3L线段垂直平分线上的点与这条线段两个端点的距离相等。如图,用一根木棒和一根弹性均匀的橡皮筋,作一个简易的“弓”,“箭”通过木棒中央的孔射出去,怎样才能保持射出去的箭的方向与木棒垂直呢?为什么?想一想:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上。例题: 如图AD⊥BC,BD=DC,点C在AE的垂直平分线上,AB、AC、CE的长度有什么关系?AB+BD与DE有什么关系?我会用!解:∵AD⊥BC,BD=DC
∴AD是BC的垂直平分线
∴AB=AC
∵点C在AE的垂直平分线上
∴AC=CE
∴ AB=AC=CE
∴ AB+BD=CE+CD=DE
即 AB+BD=DE
第一题图 第二题图 1 如图:点A和点A‘关于直线CD对称,则 __ ⊥__ , __ = __
2 如图:C是线段AB的垂直平分线上的一点,垂足为D,则下列结论中正确的有( )
①AD=BD ②AC=BC ③∠A=∠B ④∠ACD=∠BCD
⑤∠ADC=∠BDC=90°
A 2个 B 3个 C 4个 D 5个AA′ CDAO O A ′ D看看我最棒3 如图:有一块三角形田地,AB=AC=10m,作AB的垂直平分线,ED交AC于D,交AB于E,量得△BDC的周长为17m,请你帮测量人员计算BC的长.第三题图
解:∵DE垂直平分AB
∴AD=BD
∵BD+DC+BC=17
∴AD+DC+BC=17 即:AC+BC=17
又∵AC=10
∴BC=7比比谁的收获多作业:125页第3题和第5题 谢谢
