等腰三角形判定zlp[上学期]
文档属性
| 名称 | 等腰三角形判定zlp[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 514.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-11-17 19:17:00 | ||
图片预览


文档简介
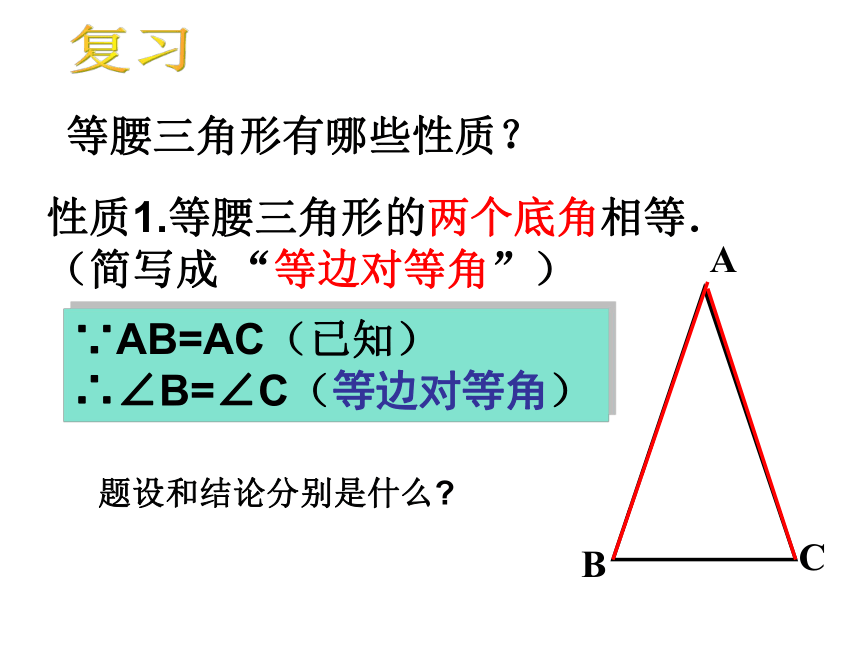
课件26张PPT。14.3.1等腰三角形(2)等腰三角形有哪些性质?性质1.等腰三角形的两个底角相等.
(简写成 “等边对等角”) ABC∵AB=AC(已知)
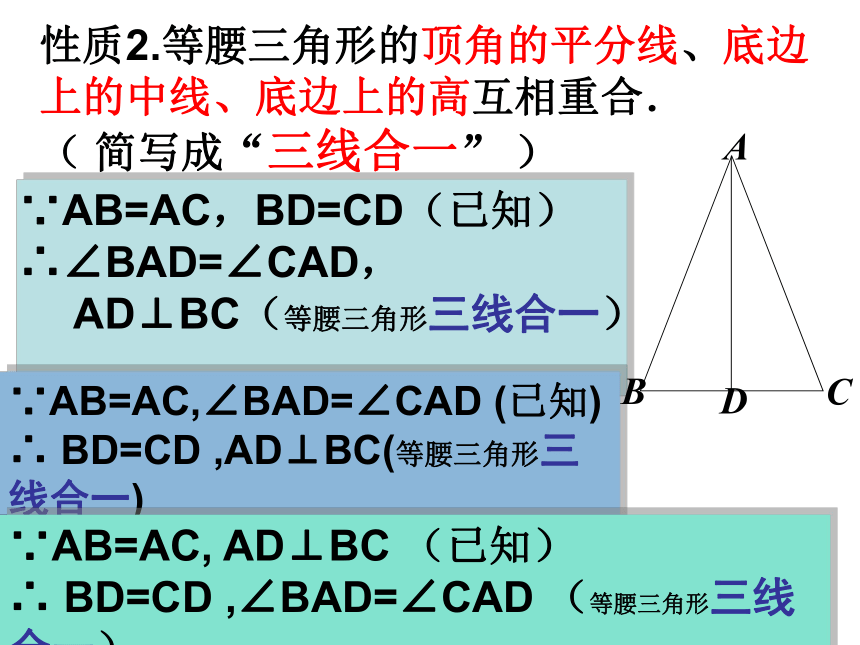
∴∠B=∠C(等边对等角)复习题设和结论分别是什么?性质2.等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合.
( 简写成“三线合一” )∵AB=AC,BD=CD(已知)
∴∠BAD=∠CAD,
AD⊥BC(等腰三角形三线合一)∵AB=AC,∠BAD=∠CAD (已知)
∴ BD=CD ,AD⊥BC(等腰三角形三线合一)∵AB=AC, AD⊥BC (已知)
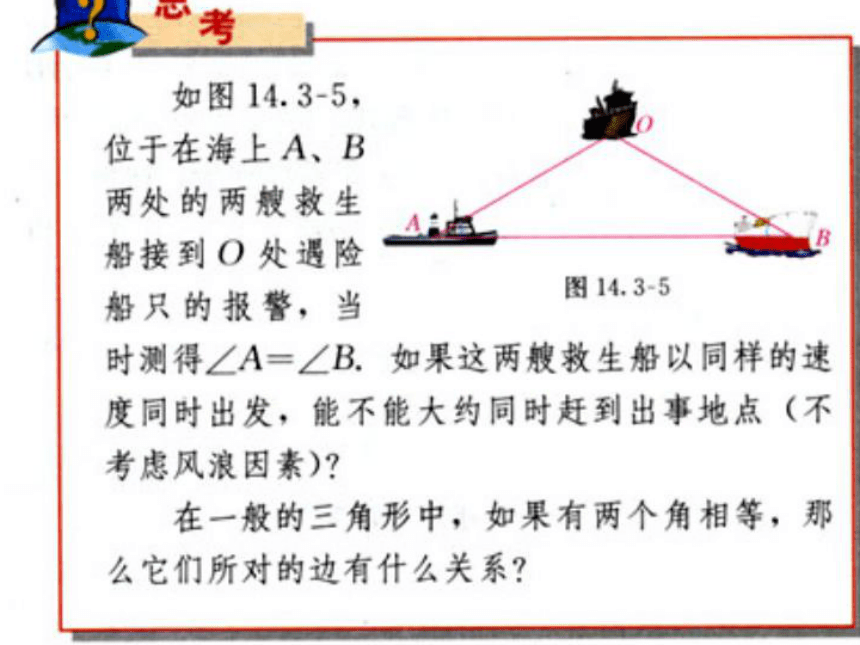
∴ BD=CD ,∠BAD=∠CAD (等腰三角形三线合一)如果一个三角形有两个角相等,
那么这两个角所对的边也相等。那么这个命题与性质1有什么关系?性质1.等腰三角形的两个底角相等.
(简写成 “等边对等角”)
它是正确的吗?你能证明吗?
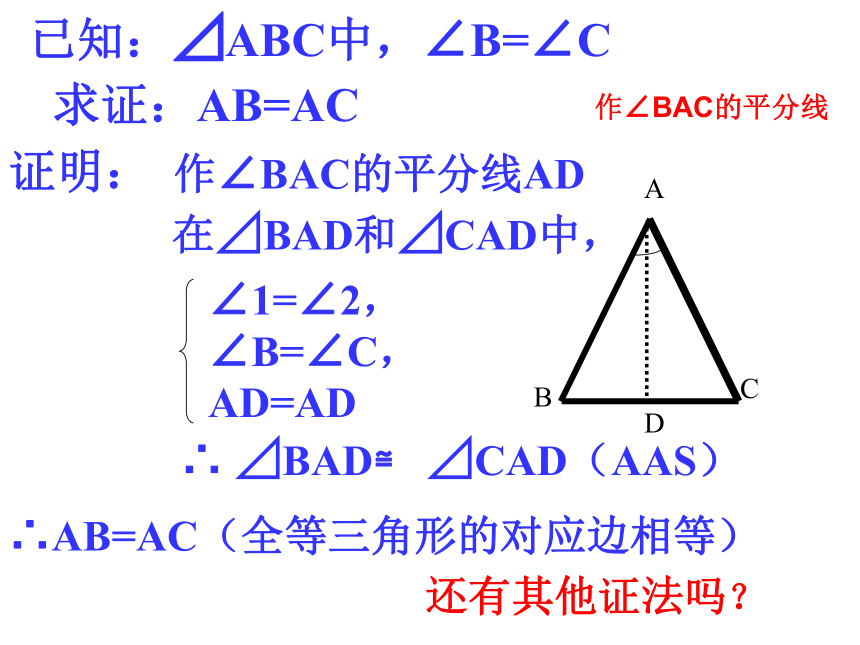
互为逆命题已知:⊿ABC中,∠B=∠C求证:AB=AC证明:作∠BAC的平分线AD在⊿BAD和⊿CAD中,∠1=∠2,
∠B=∠C,
AD=AD∴ ⊿BAD≌ ⊿CAD(AAS)∴AB=AC(全等三角形的对应边相等)还有其他证法吗?作∠BAC的平分线证明: 作BC边上的高AD.
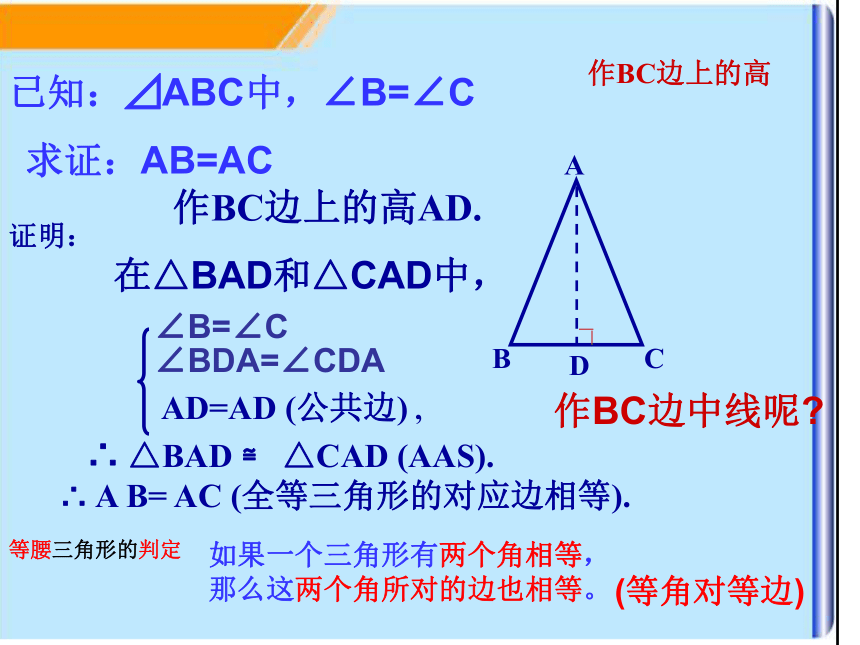
AD=AD (公共边) ,∴ △BAD ≌ △CAD (AAS).∴ A B= AC (全等三角形的对应边相等).D作BC边上的高已知:⊿ABC中,∠B=∠C求证:AB=AC在△BAD和△CAD中,∠B=∠C
∠BDA=∠CDA
作BC边中线呢?如果一个三角形有两个角相等,
那么这两个角所对的边也相等。
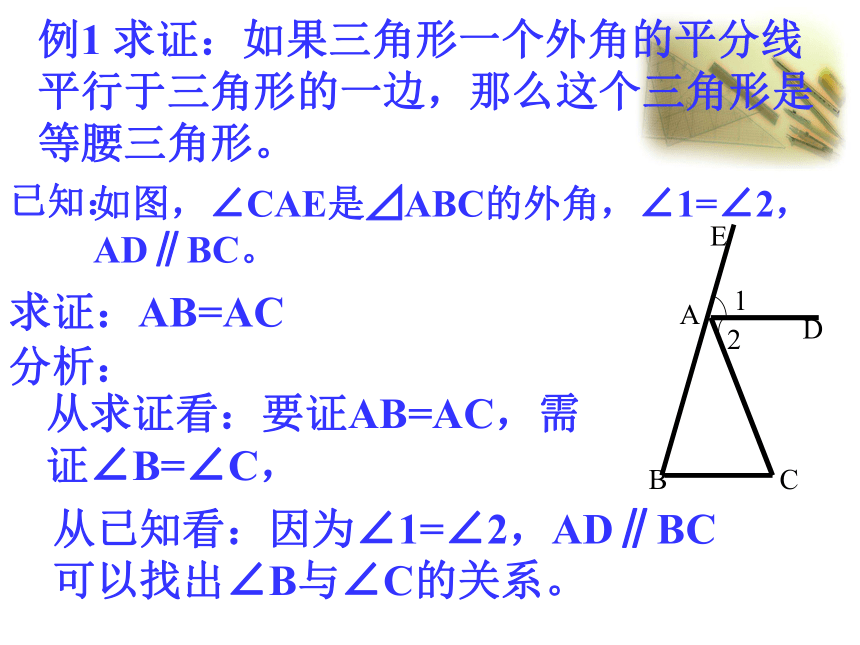
(等角对等边)等腰三角形的判定例1 求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形。求证:AB=AC分析:从求证看:要证AB=AC,需证∠B=∠C,从已知看:因为∠1=∠2,AD∥BC
可以找出∠B与∠C的关系。证明:∵AD∥BC,
∴∠1=∠B(两直线平行, 同位角相等),
∠2=∠C(两直线平行, 内错角相等)。
∵∠1=∠2,
∴∠B=∠C,
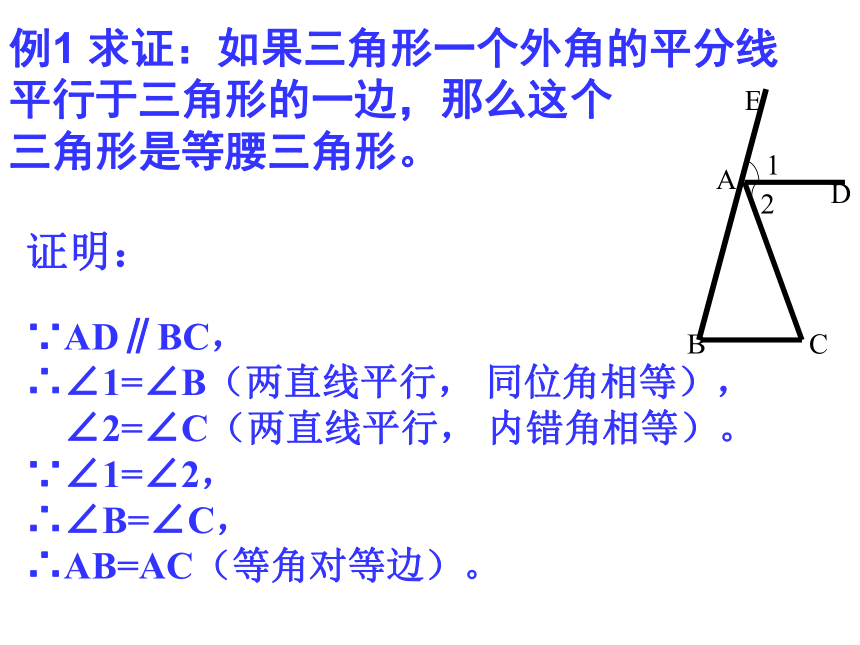
∴AB=AC(等角对等边)。例1 求证:如果三角形一个外角的平分线
平行于三角形的一边,那么这个
三角形是等腰三角形。
如图,标杆AB高为5m,为了将它固定,需要由它的中点C向地面上与点B距离相等的D、E两点拉两条绳子,使得点D、B、E在一条直线上,量得DE=4m,绳子CD和CE要多长?练习1练习1等腰直角三角形有:
⊿ABC , ⊿ACD , ⊿BCD。
练习2证明: ∵ AD ∥BC
∴∠ADB=∠DBC
∵∠ABD=∠DBC
∴∠ABD=∠ADB
∴AB=AD思考:在△ABC中,已知 ,BO平分∠ABC,CO平分∠ACB.(1)请问图中有多少个等腰三角形?说明理由.(2)线段EF和线段EB,FC之间有没有关系?若有是什么关系?AB=ACAB≠ACEF过点O作直线EF//BC交AB于E,交AC于F.研究性学习 请把这个等腰三角形纸片折成两个等腰三角形?36°⌒
ABC探究1(折成3个等腰三角形呢?…)能否把这个三角形纸片折成两个等腰三角形?探究21、对∠A进行讨论2、对∠B进行讨论3、对∠C进行讨论(分类讨论)探究220°结论:此三角形折成两个等腰三角形只有一种折法如图, △ABC中,AB=AC,D为AB上一点,E为AC延长线上一点,且BD=CE,DE交BC于G.求证:DG=EG.思路
因为△GDB和△GEC不全等,所以考虑在△GDB内作出一个与△GEC全等的三角形。★★思考题: 还有其它方法吗?ABCD已知:△ABC中,AB=AC, AD=ED=EC.CD=BC
求△ABC各角的度数。EABCD已知:如图,AB=BC=CD=ED=EF.EFMN∠MEF=105°,你能求出∠ A的度数?练习.已知:如图,在△ABC中,AB=AC,O是△ABC内一点,且OB=OC。 求证:AO⊥BCC1、今天你学会了什么?2、还有什么不懂的吗?3、有什么和老师、同学探讨的吗?作业:见作业本小结:
(简写成 “等边对等角”) ABC∵AB=AC(已知)
∴∠B=∠C(等边对等角)复习题设和结论分别是什么?性质2.等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合.
( 简写成“三线合一” )∵AB=AC,BD=CD(已知)
∴∠BAD=∠CAD,
AD⊥BC(等腰三角形三线合一)∵AB=AC,∠BAD=∠CAD (已知)
∴ BD=CD ,AD⊥BC(等腰三角形三线合一)∵AB=AC, AD⊥BC (已知)
∴ BD=CD ,∠BAD=∠CAD (等腰三角形三线合一)如果一个三角形有两个角相等,
那么这两个角所对的边也相等。那么这个命题与性质1有什么关系?性质1.等腰三角形的两个底角相等.
(简写成 “等边对等角”)
它是正确的吗?你能证明吗?
互为逆命题已知:⊿ABC中,∠B=∠C求证:AB=AC证明:作∠BAC的平分线AD在⊿BAD和⊿CAD中,∠1=∠2,
∠B=∠C,
AD=AD∴ ⊿BAD≌ ⊿CAD(AAS)∴AB=AC(全等三角形的对应边相等)还有其他证法吗?作∠BAC的平分线证明: 作BC边上的高AD.
AD=AD (公共边) ,∴ △BAD ≌ △CAD (AAS).∴ A B= AC (全等三角形的对应边相等).D作BC边上的高已知:⊿ABC中,∠B=∠C求证:AB=AC在△BAD和△CAD中,∠B=∠C
∠BDA=∠CDA
作BC边中线呢?如果一个三角形有两个角相等,
那么这两个角所对的边也相等。
(等角对等边)等腰三角形的判定例1 求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形。求证:AB=AC分析:从求证看:要证AB=AC,需证∠B=∠C,从已知看:因为∠1=∠2,AD∥BC
可以找出∠B与∠C的关系。证明:∵AD∥BC,
∴∠1=∠B(两直线平行, 同位角相等),
∠2=∠C(两直线平行, 内错角相等)。
∵∠1=∠2,
∴∠B=∠C,
∴AB=AC(等角对等边)。例1 求证:如果三角形一个外角的平分线
平行于三角形的一边,那么这个
三角形是等腰三角形。
如图,标杆AB高为5m,为了将它固定,需要由它的中点C向地面上与点B距离相等的D、E两点拉两条绳子,使得点D、B、E在一条直线上,量得DE=4m,绳子CD和CE要多长?练习1练习1等腰直角三角形有:
⊿ABC , ⊿ACD , ⊿BCD。
练习2证明: ∵ AD ∥BC
∴∠ADB=∠DBC
∵∠ABD=∠DBC
∴∠ABD=∠ADB
∴AB=AD思考:在△ABC中,已知 ,BO平分∠ABC,CO平分∠ACB.(1)请问图中有多少个等腰三角形?说明理由.(2)线段EF和线段EB,FC之间有没有关系?若有是什么关系?AB=ACAB≠ACEF过点O作直线EF//BC交AB于E,交AC于F.研究性学习 请把这个等腰三角形纸片折成两个等腰三角形?36°⌒
ABC探究1(折成3个等腰三角形呢?…)能否把这个三角形纸片折成两个等腰三角形?探究21、对∠A进行讨论2、对∠B进行讨论3、对∠C进行讨论(分类讨论)探究220°结论:此三角形折成两个等腰三角形只有一种折法如图, △ABC中,AB=AC,D为AB上一点,E为AC延长线上一点,且BD=CE,DE交BC于G.求证:DG=EG.思路
因为△GDB和△GEC不全等,所以考虑在△GDB内作出一个与△GEC全等的三角形。★★思考题: 还有其它方法吗?ABCD已知:△ABC中,AB=AC, AD=ED=EC.CD=BC
求△ABC各角的度数。EABCD已知:如图,AB=BC=CD=ED=EF.EFMN∠MEF=105°,你能求出∠ A的度数?练习.已知:如图,在△ABC中,AB=AC,O是△ABC内一点,且OB=OC。 求证:AO⊥BCC1、今天你学会了什么?2、还有什么不懂的吗?3、有什么和老师、同学探讨的吗?作业:见作业本小结:
