等腰三角形一[上学期]
图片预览






文档简介
课件30张PPT。义务教育课程标准实验教科书(人教版)第八册路桥实验中学 王万丰
2006.12.13等腰三角形教材分析评价分析学法、教法分析目标分析过程分析义务教育课程标准实验教科书(人教版)1.1 教材的地位和作用一、教材分析 小学时就接触过
等腰三角形三角形以及
全等三角形轴对称图形等腰三角形证明边角相等的
重要依据等边三角形1.2 新老教材比较一、教材分析 新教材:学习完轴对称图形、轴对称变换等之后来学习等腰三角形.
等腰三角形是轴对称图形,借助轴对称来研究等腰三角形的
一些特殊性质.老教材:介绍完等腰三角形概念和性质之后,再介绍轴对称图形有关概
念,是利用等腰三角形这种对称性来介绍轴对称图形.新教材的目的;是要将图形的变换与图形的认识、图形的性质有机的整合,利用变换
研究图形,得到图形的性质,再通过推理证明这些结论.观察图
形变换猜想推理证明性质2.1 知识与技能目标1.了解等腰三角形的概念,探索并掌握等腰三角形的特征:等腰三角形的两底角相等,底边上的高、中线及顶角平分线三线合一;
2.初步培养学生的观察-分析和归纳-概括能力,使学生初步认识特殊与一般的辩证关系.
3.能运用其特征进行对实际问题的证明与计算; 二、目标分析2.2 过程与方法目标1.培养动手能力、抽象概括能力、创新能力及用数学的意识;
2.体会一般到特殊、具体到抽象的思想方法;
3.强化类比、分类讨论、方程等思想. 2.3 情感、态度与价值观1.感受图形中的动态美、和谐美、对称美;
2.感受合作交流带来的成功感,树立自信心. 二、目标分析2.4 教学的重点和难点分析 重点:等腰三角形“等边对等角”、“三线合一”特征
的发现、探索过程; 二、目标分析难点:通过操作,如何观察、分析、归纳得出等腰三角形
的特征.3.1 学法分析 学习数学不应只是单调刻板的简单模仿、机械背诵与操练,而应该采用设置现实的问题情景,有意义的,富有挑战性的学习内容来引起学习者的兴趣。为达到提升学生的学习兴趣,我们应强调探究学习、发现学习、研究学习、合作学习才能改变学生原来的那种“学而无思,思而无疑,有疑不问”的旧学习方式.要达到学生主动的学习,本节课采用学生小组合作,实验操作,观察发现,师生互动,学生互动的学习方式.学生通过小组合作学会主动探究―――主动总结―――主动提高。突出学生是学习的主体,他们在感知知识的过程中,无疑提高了探究-发现-联想-概括的能力.三、学法、教法分析3.2 教法分析 我们在以学生为主体,展现获取知识和方法的思维过程。基于本节课的特点:课堂教学采用“情境—问题—探究—发现—创新”,使学生初步体验到数学是一个充满着观察、实验、归纳、类比和猜测的探索过程,先通过剪纸认识等腰三角形、再通过折纸发现等腰三角形性质、通过全等三角形证明。由感性认识上升到理性认识。使学生的思维由形象直观过度到抽象的逻辑演绎,层层展开,步步深入。
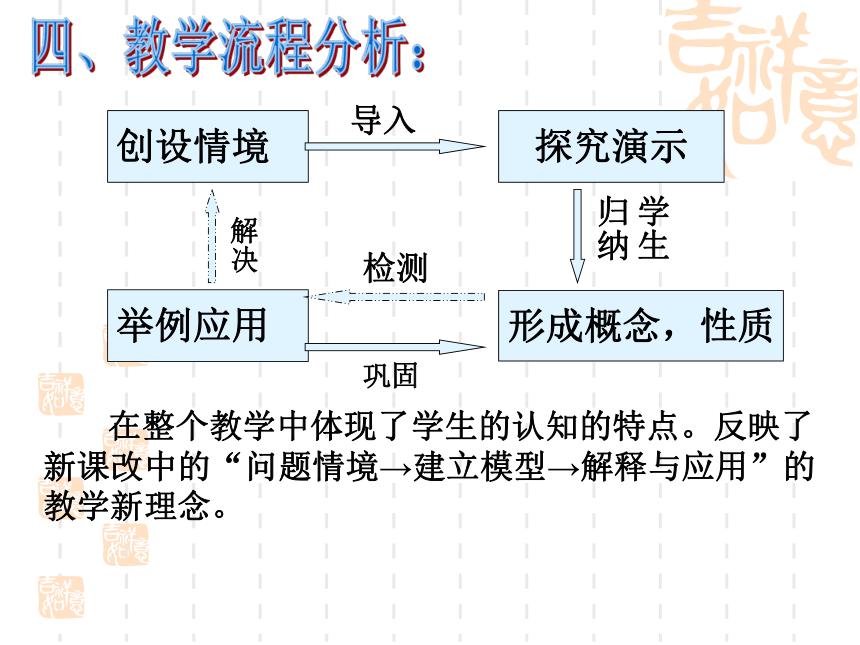
根据教材分析和目标分析,贯彻新课程改革下的课堂教学方法,确定本课主要的教法为探究发现法:学生在教师营造的“可探索”的环境里,积极参与,生动活泼地获取知识,掌握规律、主动发现、主动创新 。三、学法、教法分析创设情境探究演示举例应用形成概念,性质导入学生
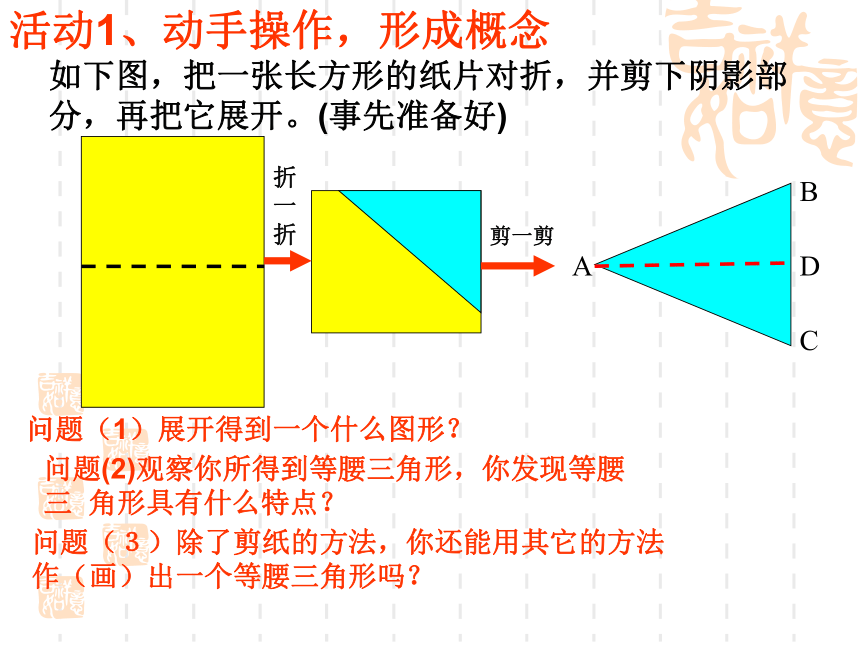
归纳巩固检测解决 在整个教学中体现了学生的认知的特点。反映了新课改中的“问题情境→建立模型→解释与应用”的教学新理念。四、教学流程分析:问题(2)观察你所得到等腰三角形,你发现等腰三 角形具有什么特点?折一折剪一剪问题(3)除了剪纸的方法,你还能用其它的方法
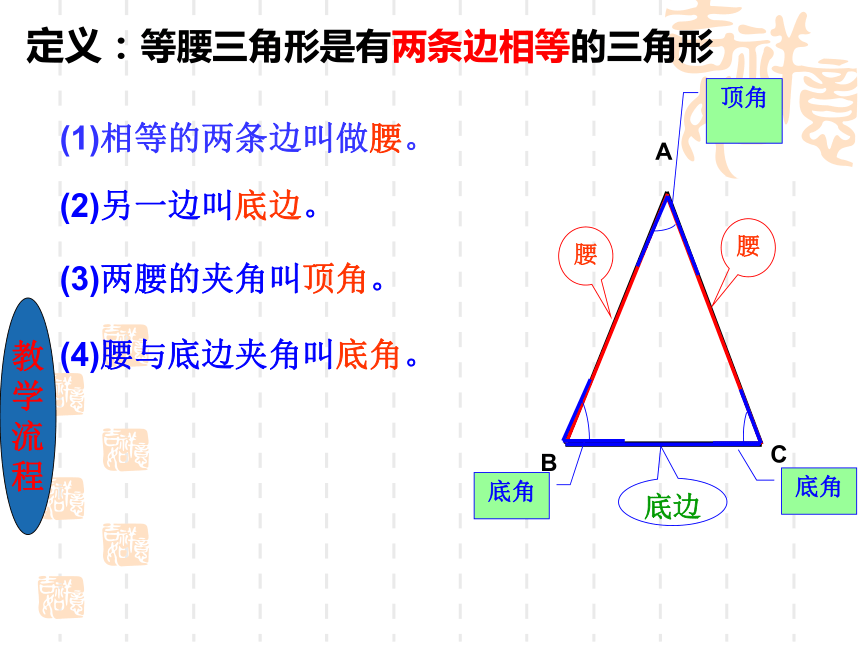
作(画)出一个等腰三角形吗?问题(1)展开得到一个什么图形? 如下图,把一张长方形的纸片对折,并剪下阴影部分,再把它展开。(事先准备好)活动1、动手操作,形成概念(1)相等的两条边叫做腰。(2)另一边叫底边。(3)两腰的夹角叫顶角。(4)腰与底边夹角叫底角。定义:等腰三角形是有两条边相等的三角形教
学
流
程 培养学生动手能力,概括表达能力,让学生知道学习数学唯一正确的方法是实行再创造,也是由学生本人把要学的东西自己去发现、动手或创造出来,教师的任务是引导和帮助学生进行这种再创造的工作,而不是把现成的知识灌输给学生.设计意图活动2、实验探索、猜想、归纳、论证特征问题1.剪出的等腰三角形是一个轴对称图形?问题2.把剪出的等腰三角形ABC沿折痕对折,找出重合的线段和角,并记录
在黑板上.问题3,根据刚刚的记录你有什么发现吗?教
学
流
程等腰三角形顶角的平分线,底边上的中线,底边上的高互相重合(三线合一).等腰三角形的两个底角相等教
学
流
程发现一:发现二:设计意图: 提高学生观察、分析问题的能力,也培养了学生归纳、概括能力。同时也要明白,观察出来东西只能作为我们的发现,它是一种特殊的情况,要说明它的正确性,还
必须经过严密的证明和逻辑推理.等腰三角形的两个底角相等。
(简写成“ 等边对等角”) AB = AC.? ? B = ?C(全等三角形的对应角相等)。已知:? A BC中, 求证: ? B =?C证明:?BAD ≌ ?CAD(SAS), ? 作? BAC 的角平分线AD教
学
流
程发现一:等腰三角形的性质一:活动3,逻辑推理,形成结论已知:
求证:△ABC中,AB = AC∠B = ∠C(1)作顶角∠ BAC的角平分线,使得∠1 = ∠ 2 , (2)作底边BC的中线 ,使得BD=CD , 教
学
流
程等腰三角形的两个底角相等(简写成“等边对等角”)在△ABC中,
∵ AC=AB( )
∴ ∠B=∠C ( )已知等边对等角教
学
流
程等腰三角形的性质一:等腰三角形的性质二:等腰三角形顶角的平分线,底边上的中线,底边上的高互相重合(三线合一).几何语言:在△ABC中
(1)∵AB=AC,AD⊥BC,
∴∠___=∠___,____=____;
(2)∵AB=AC,AD是中线,
∴∠_=∠_,____⊥____;
(3)∵AB=AC,AD是角平分线,
∴____⊥____,____=____。 12B DCD12ADBCADBCB DCD教
学
流
程几何语言:设计意图:1、让学生经历命题证明的过程,
2、培养分析、推理论证能力
3、体验辅助线在几何证明中的作用。(1)如果等腰三角形的一个底角为500,则其余两个角为____和____.(2)如果等腰三角形的顶角为800,则它的一个底角为____.5008005001.填空题(3)如果等腰三角形的一个角为800,则其余两个角为___________________.800和200(4)如果等腰三角形的一个角为1000,则其余两个角为_________.400和400或500和500活动4:应用性质,巩固新知2. 判断下列语句是否正确.(1)等腰三角形的角平分线、中线和高互相重合.( )××(5)等腰三角形的一个外角为1300,则三个内角分别:_______________________________.650、650、500或500、500、800(3)等腰三角形的底角都是锐角. ( ) (2)有一个角是60°的等腰三角形,其它两个内角也为60°. ( ) (4)钝角三角形不可能是等腰三角形 . ( )活动4:应用性质,巩固新知 例2:如图:在△ABC中,AB=AC,点D在AC上,且BC=AD=BD,求△ABC各角的度数。 灵活运用新知,巩固新知,用方程去解决几何问题,更重要是渗透方程思想,另外培养学生转化能力,如何把边的关系转化为角的关系。设计意图是:活动5:讨论探究,继续深化猜想一下,等腰三角形底边中点
到两腰的距离相等吗?你可将等腰三角形沿对称轴折
叠,观察他们的关系.继续讨论: 如果DE,DF分别是AB,AC上的中线或∠ADB, ∠ADC的平分线,他们还相等吗?由于等腰三角形是轴对称图形,利用类似的方法,还可以得到等腰三角形中那些线段相等?设计意图: 通过动手实践,增强学生的动手能力,在此过程中启迪发散学生发散思维.
同时通过引导学生合作探究,更深入
地认识等腰三角形.活动5、回顾小结,整体感知 1.知识点等腰三角形的有关概念等腰三角形的
特征轴对称图形等边对等角三线合一设计意图 引导学生自
己总结知识点、思想方法上的收获,帮助学生建构起比较完善的知识结构,归纳数学学习中常用的思想方法,从而提高他们自主学习、独立学习的能力. 这样会扼杀许多学生的学习兴趣,因而对于学生要多鼓励,以赏识教育为主,这样才能唤起学生的自信心和发展学生的潜能,所以要注重学生在数学学习过程中的评价,特别是重视学生对发现问题,解决问题的评价,五、评价分析 本设计始终体现以学生为中心的教育理念,通过数学实验激发了学生探究的兴趣,提高了他们实验、分析、探究的能力,让学生体会到实验观察、猜想、归纳、验证的思想和数形结合的思想,学生的创造力得到充分发挥,从而得出新的结论和新的猜想,因为教学过程也就是学生的认知过程,只有学生积极参与才能达到教学目的,同时通过提问、多媒体演示来突破重点,降低难点。让学生在一定情景中去经历、感悟知识,才是学生最有价值的收获,体现了学生从维持性学习走向研究性学习,从而走向自主创新性学习的转变和进步。再见谢谢指导!
2006.12.13等腰三角形教材分析评价分析学法、教法分析目标分析过程分析义务教育课程标准实验教科书(人教版)1.1 教材的地位和作用一、教材分析 小学时就接触过
等腰三角形三角形以及
全等三角形轴对称图形等腰三角形证明边角相等的
重要依据等边三角形1.2 新老教材比较一、教材分析 新教材:学习完轴对称图形、轴对称变换等之后来学习等腰三角形.
等腰三角形是轴对称图形,借助轴对称来研究等腰三角形的
一些特殊性质.老教材:介绍完等腰三角形概念和性质之后,再介绍轴对称图形有关概
念,是利用等腰三角形这种对称性来介绍轴对称图形.新教材的目的;是要将图形的变换与图形的认识、图形的性质有机的整合,利用变换
研究图形,得到图形的性质,再通过推理证明这些结论.观察图
形变换猜想推理证明性质2.1 知识与技能目标1.了解等腰三角形的概念,探索并掌握等腰三角形的特征:等腰三角形的两底角相等,底边上的高、中线及顶角平分线三线合一;
2.初步培养学生的观察-分析和归纳-概括能力,使学生初步认识特殊与一般的辩证关系.
3.能运用其特征进行对实际问题的证明与计算; 二、目标分析2.2 过程与方法目标1.培养动手能力、抽象概括能力、创新能力及用数学的意识;
2.体会一般到特殊、具体到抽象的思想方法;
3.强化类比、分类讨论、方程等思想. 2.3 情感、态度与价值观1.感受图形中的动态美、和谐美、对称美;
2.感受合作交流带来的成功感,树立自信心. 二、目标分析2.4 教学的重点和难点分析 重点:等腰三角形“等边对等角”、“三线合一”特征
的发现、探索过程; 二、目标分析难点:通过操作,如何观察、分析、归纳得出等腰三角形
的特征.3.1 学法分析 学习数学不应只是单调刻板的简单模仿、机械背诵与操练,而应该采用设置现实的问题情景,有意义的,富有挑战性的学习内容来引起学习者的兴趣。为达到提升学生的学习兴趣,我们应强调探究学习、发现学习、研究学习、合作学习才能改变学生原来的那种“学而无思,思而无疑,有疑不问”的旧学习方式.要达到学生主动的学习,本节课采用学生小组合作,实验操作,观察发现,师生互动,学生互动的学习方式.学生通过小组合作学会主动探究―――主动总结―――主动提高。突出学生是学习的主体,他们在感知知识的过程中,无疑提高了探究-发现-联想-概括的能力.三、学法、教法分析3.2 教法分析 我们在以学生为主体,展现获取知识和方法的思维过程。基于本节课的特点:课堂教学采用“情境—问题—探究—发现—创新”,使学生初步体验到数学是一个充满着观察、实验、归纳、类比和猜测的探索过程,先通过剪纸认识等腰三角形、再通过折纸发现等腰三角形性质、通过全等三角形证明。由感性认识上升到理性认识。使学生的思维由形象直观过度到抽象的逻辑演绎,层层展开,步步深入。
根据教材分析和目标分析,贯彻新课程改革下的课堂教学方法,确定本课主要的教法为探究发现法:学生在教师营造的“可探索”的环境里,积极参与,生动活泼地获取知识,掌握规律、主动发现、主动创新 。三、学法、教法分析创设情境探究演示举例应用形成概念,性质导入学生
归纳巩固检测解决 在整个教学中体现了学生的认知的特点。反映了新课改中的“问题情境→建立模型→解释与应用”的教学新理念。四、教学流程分析:问题(2)观察你所得到等腰三角形,你发现等腰三 角形具有什么特点?折一折剪一剪问题(3)除了剪纸的方法,你还能用其它的方法
作(画)出一个等腰三角形吗?问题(1)展开得到一个什么图形? 如下图,把一张长方形的纸片对折,并剪下阴影部分,再把它展开。(事先准备好)活动1、动手操作,形成概念(1)相等的两条边叫做腰。(2)另一边叫底边。(3)两腰的夹角叫顶角。(4)腰与底边夹角叫底角。定义:等腰三角形是有两条边相等的三角形教
学
流
程 培养学生动手能力,概括表达能力,让学生知道学习数学唯一正确的方法是实行再创造,也是由学生本人把要学的东西自己去发现、动手或创造出来,教师的任务是引导和帮助学生进行这种再创造的工作,而不是把现成的知识灌输给学生.设计意图活动2、实验探索、猜想、归纳、论证特征问题1.剪出的等腰三角形是一个轴对称图形?问题2.把剪出的等腰三角形ABC沿折痕对折,找出重合的线段和角,并记录
在黑板上.问题3,根据刚刚的记录你有什么发现吗?教
学
流
程等腰三角形顶角的平分线,底边上的中线,底边上的高互相重合(三线合一).等腰三角形的两个底角相等教
学
流
程发现一:发现二:设计意图: 提高学生观察、分析问题的能力,也培养了学生归纳、概括能力。同时也要明白,观察出来东西只能作为我们的发现,它是一种特殊的情况,要说明它的正确性,还
必须经过严密的证明和逻辑推理.等腰三角形的两个底角相等。
(简写成“ 等边对等角”) AB = AC.? ? B = ?C(全等三角形的对应角相等)。已知:? A BC中, 求证: ? B =?C证明:?BAD ≌ ?CAD(SAS), ? 作? BAC 的角平分线AD教
学
流
程发现一:等腰三角形的性质一:活动3,逻辑推理,形成结论已知:
求证:△ABC中,AB = AC∠B = ∠C(1)作顶角∠ BAC的角平分线,使得∠1 = ∠ 2 , (2)作底边BC的中线 ,使得BD=CD , 教
学
流
程等腰三角形的两个底角相等(简写成“等边对等角”)在△ABC中,
∵ AC=AB( )
∴ ∠B=∠C ( )已知等边对等角教
学
流
程等腰三角形的性质一:等腰三角形的性质二:等腰三角形顶角的平分线,底边上的中线,底边上的高互相重合(三线合一).几何语言:在△ABC中
(1)∵AB=AC,AD⊥BC,
∴∠___=∠___,____=____;
(2)∵AB=AC,AD是中线,
∴∠_=∠_,____⊥____;
(3)∵AB=AC,AD是角平分线,
∴____⊥____,____=____。 12B DCD12ADBCADBCB DCD教
学
流
程几何语言:设计意图:1、让学生经历命题证明的过程,
2、培养分析、推理论证能力
3、体验辅助线在几何证明中的作用。(1)如果等腰三角形的一个底角为500,则其余两个角为____和____.(2)如果等腰三角形的顶角为800,则它的一个底角为____.5008005001.填空题(3)如果等腰三角形的一个角为800,则其余两个角为___________________.800和200(4)如果等腰三角形的一个角为1000,则其余两个角为_________.400和400或500和500活动4:应用性质,巩固新知2. 判断下列语句是否正确.(1)等腰三角形的角平分线、中线和高互相重合.( )××(5)等腰三角形的一个外角为1300,则三个内角分别:_______________________________.650、650、500或500、500、800(3)等腰三角形的底角都是锐角. ( ) (2)有一个角是60°的等腰三角形,其它两个内角也为60°. ( ) (4)钝角三角形不可能是等腰三角形 . ( )活动4:应用性质,巩固新知 例2:如图:在△ABC中,AB=AC,点D在AC上,且BC=AD=BD,求△ABC各角的度数。 灵活运用新知,巩固新知,用方程去解决几何问题,更重要是渗透方程思想,另外培养学生转化能力,如何把边的关系转化为角的关系。设计意图是:活动5:讨论探究,继续深化猜想一下,等腰三角形底边中点
到两腰的距离相等吗?你可将等腰三角形沿对称轴折
叠,观察他们的关系.继续讨论: 如果DE,DF分别是AB,AC上的中线或∠ADB, ∠ADC的平分线,他们还相等吗?由于等腰三角形是轴对称图形,利用类似的方法,还可以得到等腰三角形中那些线段相等?设计意图: 通过动手实践,增强学生的动手能力,在此过程中启迪发散学生发散思维.
同时通过引导学生合作探究,更深入
地认识等腰三角形.活动5、回顾小结,整体感知 1.知识点等腰三角形的有关概念等腰三角形的
特征轴对称图形等边对等角三线合一设计意图 引导学生自
己总结知识点、思想方法上的收获,帮助学生建构起比较完善的知识结构,归纳数学学习中常用的思想方法,从而提高他们自主学习、独立学习的能力. 这样会扼杀许多学生的学习兴趣,因而对于学生要多鼓励,以赏识教育为主,这样才能唤起学生的自信心和发展学生的潜能,所以要注重学生在数学学习过程中的评价,特别是重视学生对发现问题,解决问题的评价,五、评价分析 本设计始终体现以学生为中心的教育理念,通过数学实验激发了学生探究的兴趣,提高了他们实验、分析、探究的能力,让学生体会到实验观察、猜想、归纳、验证的思想和数形结合的思想,学生的创造力得到充分发挥,从而得出新的结论和新的猜想,因为教学过程也就是学生的认知过程,只有学生积极参与才能达到教学目的,同时通过提问、多媒体演示来突破重点,降低难点。让学生在一定情景中去经历、感悟知识,才是学生最有价值的收获,体现了学生从维持性学习走向研究性学习,从而走向自主创新性学习的转变和进步。再见谢谢指导!
