第20课《谈创造性思维》课件(共64张PPT)
文档属性
| 名称 | 第20课《谈创造性思维》课件(共64张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 统编版 | ||
| 科目 | 语文 | ||
| 更新时间 | 2022-10-20 21:10:53 | ||
图片预览










文档简介
(共64张PPT)
导入新课
“横看成岭侧成峰,远近高低各不同”说明了同一事物在不同的观察角度下会有不同的理解和感受。由此可见,事物的正确答案并不是唯一的。这是为什么呢?带着这个疑问,我们一起来学习19课吧。
课文的题目是作者要论述的观点。题目用了一个判断句,通俗易懂而又旗帜鲜明地表明:同一个问题从不同的角度考虑会有不同的答案.作者是在借此阐述创造性思维的问题。
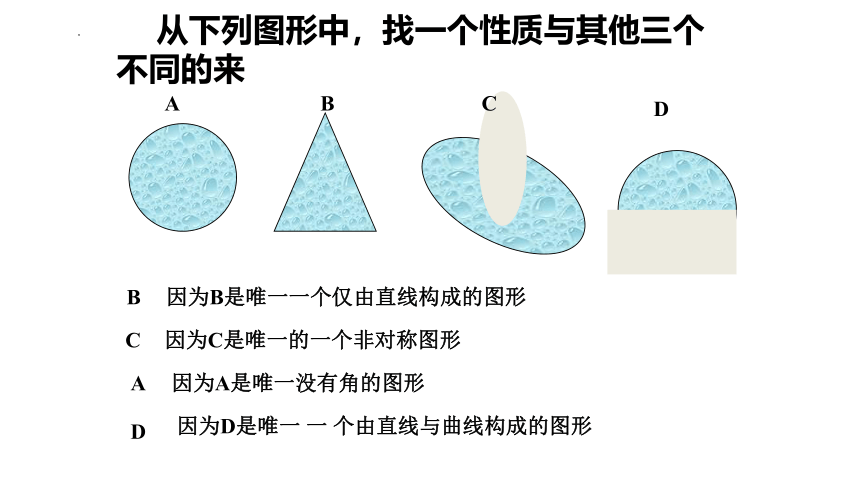
从下列图形中,找一个性质与其他三个不同的来
因为C是唯一的一个非对称图形
因为B是唯一一个仅由直线构成的图形
因为A是唯一没有角的图形
因为D是唯一 一 个由直线与曲线构成的图形
B
C
A
D
A
B
C
D
6
是“6”
不,是“9”
漫画:《谁也没有错》
看一看:图中是什么?
1+1=?
“一把锯子 + 一片森林
一支笔 + 一张纸
一个李白+ 一壶酒”
生活实例
一片荒漠…
一幅画、一首诗、一首歌、一个世界…
诗百篇
1、赵本山出题:“1+1在什么情况下不等于2”?
范伟答:“1+1在任何情况下都等于2”。
来看小品《卖车》中的一段话
高秀敏纠正:“1+1在答错的情况下不等于2。”
2、赵本山问:“你家养了一只小狗,为什么不生跳蚤?”
范伟答:“因为我们家小狗讲卫生。”
赵本山:“错。媳妇答。”
高秀敏答:“因为狗只能生狗。”
3、赵本山问:“一位80岁的老奶奶上了公共汽车,车上没一个人给他让座,为什么?”
范伟答:“因为车上的人不讲文明礼貌。”
高秀敏纠正:“因为车上有的是空座。”
题西林壁
横看成岭侧成峰,
远近高低各不同。
不识庐山真面目,
只缘身在此山中。
《题西林壁》:“横看成岭侧成峰,远近高低各不同。不识庐山真面目,只缘身在此山中。”“横看成岭侧成峰,远近高低各不同”说明什么?对同一事物在不同的观察角度下会有不同的理解和感受。由此可见,事物的正确答案并不是唯一的,这是为什么呢?带着这个疑问我们一起来学习《谈创造性思维》。
导入新知
谈创造性思维
罗迦.费.因格
1.学习课文的论证方式及其方法。
2.认真赏析本文语言,体会设问的作用。
3.理解富有创造力的人与缺乏创造力的人之间的区别,并领会创造性思维在实际生活中的重大意义。
学习目标
罗迦·费·因格,1948年生,当代美
国实业家、学者、创造学家,是“创意思
考顾问公司”的创立人与总裁。曾任加利
福利亚创意顾问。著作有《当头棒喝》、
《创造性纸牌》等,“唯一真正快乐的人
们是儿童和富有创造性的那一部分人”是他的名言。
简介作者
许多人在生活、学习的过程中因受传统思想的影响,容易形成固定的思维模式,他们只知道死学知识而不知活用,不会跳出圈外去思考问题。生活中还有许多人以为搞发明和创造的都是天才人物,不相信自己也能有所发明和创造,结果导致创造性被自我压制,最终丧失。本文正是针对这种情况而写的。作者想要说明,有过许多发明创造的人最初也是和大家一样的普通人,而普通人只要有自信,不断学习知识,活用知识,敢于打破常规思考问题,就会成为一个有所发明、有所创造的人。
简介背景
读准字音
罗迦jiā 模mó式
汲jí取 恭gōng喜
依赖lài 波澜lán壮阔
根深蒂dì固 孜zī孜不倦
锲qiè而不舍 不言而喻yù
渊博bó 对称chèn
压榨zhà 推敲qiāo
学习词语
探求tàn qiú探索追求。
创意chuàng yì创造性的见解或意境。
压榨yā zhà挤出汁水或内含物。或比喻剥削或搜刮
根深蒂固gēn shēn dì gù比喻根基牢固,不可动摇。
行之有效xíng zhī yǒu xiào实行起来有成效。多指方法或措施被实践证明有效。
孜孜不倦zī zī bú juàn勤奋努力,不知疲倦。孜孜:勤勉。
持之以恒chí zhī yǐ héng长久地坚持下去。恒,恒心。
不言而喻bù yán ér yù不用说就可以明白。喻,明白。
轻而易举qīng ér yì jǔ形容做事毫不费劲,非常容易。
模式mó shì某种事物的标准形式或使人可以照着做的标准样式。
汲取jí qǔ吸取。汲,从下往上打水。
一事无成yī shì wú chéng一件事也没有办成。形容毫无成绩。
灵感líng gǎn一种人们无法控制。创造力高度发挥的突发性心理现象。
推敲tuī qiāo比喻斟酌字句,反复琢磨。
锲而不舍qiè ér bù shě雕刻一件东西,一直刻下去不放手。比喻有恒心,有毅力。锲,雕刻。
快速读课文,思考:
1.根据课文内容,说说作者首先告诉了我们一个什么观点。
2.读完课文,归纳一下本文提出的观点。
整体感知
作者在文章中首先告诉了我们事物的正确答案不止一个。
1. 根据课文内容,说说作者首先告诉了我们一个什么观点。
2.读完课文,归纳一下本文提出的观点。
(1) 事物的正确答案不止一个 (1-3)
(2) 创造性思维必需的要素(4-8)
(3) 是否人人都有创造力( 9-12)
(4) 怎样成为有创造力的人(13)
浏览课文内容,思考下面问题:
1.本文的开头有什么特点?有什么好处?
3.创造性思维有哪些必要的要素?
2.为什么说“事物的正确答案不止一个”?
4.是否拥有创造力的依据是什么?
精读细研
画出四个图形,提出一个问题。用问题引出论点,结合问题讲道理。
从下列四种图形中,找出一个性质与其他三个不同的来。
1.本文的开头有什么特点?
A 唯一的没有角的图形。
B 唯一的仅由直线构成的图形。
C 唯一的非对称性图形。
D 唯一由直线和曲线构成的图形。
结论:由于看图形的角度不同,四种答案全都正确。
即:事物的正确答案不止一个(提出论点)
说一说:这种开头方法有什么好处
新颖别致,使抽象的议论显得生动形象,通俗易懂,能引起读者的阅读兴趣。
不满足于一个答案,不放弃探求
这一点非常重要
“正确答案只有一个”这种思维模式,在我们头脑中已不知不觉地根深蒂固。这篇课文却提出相反观点,要求我们:
2.为什么说“事物的正确答案不止一个”?
由于背景的不同,考虑问题角度的变化,知识积累的差异等原因,事物的正确答案往往不止一个。
3.创造性思维有哪些必要的要素?
(1)有渊博的知识。
(2)有探求新事物,并为此而活用知识的态度和意识。
(3)有持之以恒的精神和毅力(不断地尝试)。
有渊博的知识 。
“这种情况可能出现在6分钟之后……”。“这种情况”指代什么?“它”指代什么?
“这种情况”指代“这些知识随时都可以进行组合,形成新的创意”。“它”指代“新的创意”。
有渊博的知识。
“我对此完全赞同”的“此”指什么?
富有创造力的人总是孜孜不倦地汲取知识,使自己学识渊博。
为什么“我对此完全赞同”?
因为“知识是形成新创意的素材”。
作者是如何来论证他的观点的?
举例论证
B.罗兰·布歇内尔把电视接收器作为试验对象,发明了交互式的乒乓球电子游戏,从此开始了游戏机的革命。
发挥创造力的真正关键,在于如何运用知识。
②有探求新事物并为此而活用知识的态度和意识。
A.谷登堡将葡萄压榨机和硬币打制器组合起来,发明了印刷机和排版术。
③有持之以恒的精神和毅力(不断地尝试)。
请补充一些例子来证明创造必须要有持之以恒的精神和毅力。
A.丁肇中在两年多的夜以继日的实验中发现了J粒子。
B.爱迪生用多种金属丝做实验,前后试过的材料不下1600种,终于发明了电灯。
C.居里夫人从几十吨的矿渣中提炼出不到1克的镭!
方法指导
补充论据
考点解说:
论据,是支撑论点的材料,是作者用来证明论点的理由和根据。根据论点补充论据,是近年来常见的题型,看起来要求比较宽泛,但补写的论据也要求典型,有代表性,说服力强。补写的论据不外乎两种形式:事实论据和道理论据。
考查方式:
你能否为要证明的论点再补充一个典型事例或一句名言警句?请选出最能证明论点的论据或请选出不能作为论据的一项。
方法点拨:
做这类题目,要注意以下两个方面:
1.看清楚要求补充的论据类型。
即看清楚要求补充的是名言还是事例;
2.补充名人事例要注意字数限制。
在日常学习生活中,我们可准备些关于“勤奋”“处世”“诚信”
“责任”“信念”等常见主题的名人事例和名言。名言的字数要少,事例要熟悉,不要为求新而准备那些较长的名言或不熟悉的名人事例。
补充原则:真实、典型,能够证明论点。
答题方式:人物+事例+简短评价。
4.是否拥有创造力的依据是什么?
不过,这种创造性的思维是否任何人都具备呢?是否存在富有创造力的人和缺乏创造力的人的区别呢?
由两个问句引出下文论述的具体内容。在结构上起承接、过渡作用。
不认为自己具有创造力
区分二者的根据之一是
拥有创造力的人留意自己细小的想法
区分一个人是否拥有创造力的主要依据:
富于创造力的人
缺乏创造力的人
认为自己具有创造力
结论:人人都具有创造力
1.有人说只有贝多芬、爱因斯坦以及莎士比亚才具备创造性思维,你同意这种观点吗?联系自己的生活经验谈谈你的看法。
合作探究
不同意。在大多数情况下,即便是他们,也并非轻而易举就能获得如此非凡的灵感。相反,这种非凡的灵感,往往产生于这样的过程:关注极其普通,甚至一闪念的想法,并对它反复推敲,逐渐充实。
我们每个人都有无限的潜能和创造力,而这个创造力可以无止境地运用于我们生活中的每个角落。我们最需要问自己的一个问题并非我们是否有创造力,而是如何能够发现并发挥他的潜能和创造力,这也是影响自身创造力是否发挥的根本。
示例:
2.怎样才能做一个富有创造力的人呢?
(1)要经常保持好奇心,不断积累知识。
(2)不满足于一个答案,而去探求新思路,去运用所获得的知识。
(3)一旦产生小的灵感,相信它的价值,并锲而不舍地把它发展下去。
3.你认为发挥创造力的关键是什么?
如何运用知识
首先坚信任何人都拥有创造力,留意自己细小的想法,小的创意会打开大的突破口,并坚信自己一定能使之变为现实。
主要论述怎样才能拥有创造力的问题。
关于创造性必需的三个要素,经过课文逐层论述,最后才给出答案,这合乎“分→总”这种思维规律,便于读者理解和把握。
4.本文主要论述了什么问题?关于创造性思维所必需的要素,为什么到篇末才给出全部答案?
①然而在大多数情况下,即便是他们,也并非轻而易举就能获得如此非凡的灵感。
5.赏析语言,说说下列句子中画横线的词语能否删去?为什么?
不能删去。“大多数”一词强调了获得灵感多数情况下并非轻而易举,但也有轻而易举获得灵感的时候。这一词语体现了议论文语言的严密性。
②富有创造力的人总是孜孜不倦地汲取知识,使自己学识渊博。
不能删去。“总是”强调了富有创造性的人能够长时间的、孜孜不倦地汲取知识,如果删去了就没有强调的意味,表示的范围也不明确。
③发挥创造力的真正关键,在于如何运用知识。
不能删去。“真正关键”强调了“如何运用知识”是发挥创造力的最重要的必需的要素,如果删去,则表明该要素是一般的, 无突出强调的效果。
④区分一个人是否拥有创造力,主要根据之一是,拥有创造力的人留意自己细小的想法。
不能删去。“之一”表示区分一个人是否具有创造力,除了这一根据之外,还有别的根据,如果删去,就显得太绝对,体现不了议论文语言的严密性。
本文由一个选择题入手,阐述什么是创造性思维,以及怎样才能成为一个有创造力的人,号召人们坚信自己的创造力,努力保持好奇心,不断探求,成为富有创造力的人。
概括主题
长期以来,人们习惯了“正确答案只有一个”的思维模式,其实在我们的生活中,很多事物的答案并不是唯一的。同一个事物,从不同的角度来观察,会得出不同的结论。生活是五彩缤纷的,我们要处处留心,关注细节,成为一个富有创造力的人。
学后感悟
课文先用四个图形提出一个题,引出“事物的正确答案不止一个”的观点。接着,作者从“事物的正确答案不止一个”,引申出了“不满足于一个答案,不放弃探求,这一点非常重要”。既然不满足于一个答案,就需要寻求其他答案,那么怎样寻求呢?于是课文顺理成章地提出“有赖于创造性的思维”。紧接着,又引申出如下问题:“不过,这种创造性的思维是否任何人都具备呢?是否存在富有创造力的人和缺乏创造力的人的区别呢?”接下来的论述就是回答这个问题的。最后,课文得出结论:“任何人都拥有创造力”。只要具备几个关键性的要素,就能成为一个富有创造力的人。
围绕中心,逐层论述。
写作特色
例如:“若是某种数学问题的话,说正确答案只有一个是对的。”在此强调数学问题,这种用语是非常准确、严密的。因为数学问题的答案,一就是一,二就是二,思维的方式可以多样,但问题的答案只有一个。
语言准确、严密。
1.数学问题→生活问题:“事物的正确答案不止一个”
2.探求第二种答案有赖于创造性思维。
3. 任何人都拥有创造力,关键要具备三个要素。
必需要素
区分根据
a. 渊博的知识
b. 活用知识的态度和意识
c. 持之以恒的毅力
a.缺乏的人:自我压制
b.拥有的人:留意细小的想法,并相信自己
谈创造性思维
板书设计
A. 孜孜不倦(勤勉) 汲取(吸)
B. 持之以恒(恒心) 素材(材料)
C. 不言而喻(明白) 创意(创造性)
D. 锲而不舍(雕刻) 根深蒂固(花或瓜果与枝茎相连的部分)
1. 下列画线词语解释有误的一项是( )
【解析】“素”的意思是未经提炼和加工的;原始的。
B
课堂练习
(1)富有创造力的人总是孜孜不倦地 (汲取 学习)知识,使自己 (学识 学问)渊博。
(2)知识是形成新创意的 (材料 素材)。 但这并不是说,光凭知识就能拥有 (创造性 创造力)。
2.选词填空。
汲取
学识
素材
创造力
3.同一个问题,从不同的角度分析,可以得出不同的结论,正如罗迦·费·因格所说的“事物的正确答案不止一个”请你以不同角度从《龟兔赛跑》的故事中提炼观点(至少两个)。
示例:
1.万物没有绝对的
2.只要努力就有可能
B
课后练习
A
B
不能。如果把“主要”和“之一”去掉,就变成了“留意自己细小的想法”是拥有创造力的唯一根据,这与事实不符;这两个词很好地体现了议论文语言的准确性。
“并非轻而易举”体现了议论文语言的准确性、严密性,它准确地说明了灵感的产生是积累、活用知识的产物。
示例:说明了国家重视科技创新,全社会积极创新。
示例一:第一幅更好。第一幅图简洁明了,要素是“创”字和两只手,意思是用双手创造。双手造型像展开的双翼,寓意是“创客很棒”,比喻进步腾飞。示例二:第二幅更好。第二幅图上有许多人,年龄、性别、身份不同,表示大众创业、万众创新;上面有灯光,表明创新、创造给人们的生活带来光明,照亮每个人的未来。这幅图寓意更深刻,引人沉思。
想一想:
玩24点扑克牌的游戏:用5、6、
3、3、四 张牌通过加减乘除的运算得
出24这个结果, 每张牌只能用一次。
考考你
发挥想象,下面的图形会是什么
关于小鸡过马路的话题
拿破仑:不想过马路的鸡不是好鸡。
爱因斯坦:小鸡的成功=勇敢的穿越+正确的方法+少说空话。
达尔文:鸡从森林来到人家再发展到马路,这是优胜劣汰的进化法则。
阿基米德:只要给我一条马路,我就能让小鸡走过去。
导入新课
“横看成岭侧成峰,远近高低各不同”说明了同一事物在不同的观察角度下会有不同的理解和感受。由此可见,事物的正确答案并不是唯一的。这是为什么呢?带着这个疑问,我们一起来学习19课吧。
课文的题目是作者要论述的观点。题目用了一个判断句,通俗易懂而又旗帜鲜明地表明:同一个问题从不同的角度考虑会有不同的答案.作者是在借此阐述创造性思维的问题。
从下列图形中,找一个性质与其他三个不同的来
因为C是唯一的一个非对称图形
因为B是唯一一个仅由直线构成的图形
因为A是唯一没有角的图形
因为D是唯一 一 个由直线与曲线构成的图形
B
C
A
D
A
B
C
D
6
是“6”
不,是“9”
漫画:《谁也没有错》
看一看:图中是什么?
1+1=?
“一把锯子 + 一片森林
一支笔 + 一张纸
一个李白+ 一壶酒”
生活实例
一片荒漠…
一幅画、一首诗、一首歌、一个世界…
诗百篇
1、赵本山出题:“1+1在什么情况下不等于2”?
范伟答:“1+1在任何情况下都等于2”。
来看小品《卖车》中的一段话
高秀敏纠正:“1+1在答错的情况下不等于2。”
2、赵本山问:“你家养了一只小狗,为什么不生跳蚤?”
范伟答:“因为我们家小狗讲卫生。”
赵本山:“错。媳妇答。”
高秀敏答:“因为狗只能生狗。”
3、赵本山问:“一位80岁的老奶奶上了公共汽车,车上没一个人给他让座,为什么?”
范伟答:“因为车上的人不讲文明礼貌。”
高秀敏纠正:“因为车上有的是空座。”
题西林壁
横看成岭侧成峰,
远近高低各不同。
不识庐山真面目,
只缘身在此山中。
《题西林壁》:“横看成岭侧成峰,远近高低各不同。不识庐山真面目,只缘身在此山中。”“横看成岭侧成峰,远近高低各不同”说明什么?对同一事物在不同的观察角度下会有不同的理解和感受。由此可见,事物的正确答案并不是唯一的,这是为什么呢?带着这个疑问我们一起来学习《谈创造性思维》。
导入新知
谈创造性思维
罗迦.费.因格
1.学习课文的论证方式及其方法。
2.认真赏析本文语言,体会设问的作用。
3.理解富有创造力的人与缺乏创造力的人之间的区别,并领会创造性思维在实际生活中的重大意义。
学习目标
罗迦·费·因格,1948年生,当代美
国实业家、学者、创造学家,是“创意思
考顾问公司”的创立人与总裁。曾任加利
福利亚创意顾问。著作有《当头棒喝》、
《创造性纸牌》等,“唯一真正快乐的人
们是儿童和富有创造性的那一部分人”是他的名言。
简介作者
许多人在生活、学习的过程中因受传统思想的影响,容易形成固定的思维模式,他们只知道死学知识而不知活用,不会跳出圈外去思考问题。生活中还有许多人以为搞发明和创造的都是天才人物,不相信自己也能有所发明和创造,结果导致创造性被自我压制,最终丧失。本文正是针对这种情况而写的。作者想要说明,有过许多发明创造的人最初也是和大家一样的普通人,而普通人只要有自信,不断学习知识,活用知识,敢于打破常规思考问题,就会成为一个有所发明、有所创造的人。
简介背景
读准字音
罗迦jiā 模mó式
汲jí取 恭gōng喜
依赖lài 波澜lán壮阔
根深蒂dì固 孜zī孜不倦
锲qiè而不舍 不言而喻yù
渊博bó 对称chèn
压榨zhà 推敲qiāo
学习词语
探求tàn qiú探索追求。
创意chuàng yì创造性的见解或意境。
压榨yā zhà挤出汁水或内含物。或比喻剥削或搜刮
根深蒂固gēn shēn dì gù比喻根基牢固,不可动摇。
行之有效xíng zhī yǒu xiào实行起来有成效。多指方法或措施被实践证明有效。
孜孜不倦zī zī bú juàn勤奋努力,不知疲倦。孜孜:勤勉。
持之以恒chí zhī yǐ héng长久地坚持下去。恒,恒心。
不言而喻bù yán ér yù不用说就可以明白。喻,明白。
轻而易举qīng ér yì jǔ形容做事毫不费劲,非常容易。
模式mó shì某种事物的标准形式或使人可以照着做的标准样式。
汲取jí qǔ吸取。汲,从下往上打水。
一事无成yī shì wú chéng一件事也没有办成。形容毫无成绩。
灵感líng gǎn一种人们无法控制。创造力高度发挥的突发性心理现象。
推敲tuī qiāo比喻斟酌字句,反复琢磨。
锲而不舍qiè ér bù shě雕刻一件东西,一直刻下去不放手。比喻有恒心,有毅力。锲,雕刻。
快速读课文,思考:
1.根据课文内容,说说作者首先告诉了我们一个什么观点。
2.读完课文,归纳一下本文提出的观点。
整体感知
作者在文章中首先告诉了我们事物的正确答案不止一个。
1. 根据课文内容,说说作者首先告诉了我们一个什么观点。
2.读完课文,归纳一下本文提出的观点。
(1) 事物的正确答案不止一个 (1-3)
(2) 创造性思维必需的要素(4-8)
(3) 是否人人都有创造力( 9-12)
(4) 怎样成为有创造力的人(13)
浏览课文内容,思考下面问题:
1.本文的开头有什么特点?有什么好处?
3.创造性思维有哪些必要的要素?
2.为什么说“事物的正确答案不止一个”?
4.是否拥有创造力的依据是什么?
精读细研
画出四个图形,提出一个问题。用问题引出论点,结合问题讲道理。
从下列四种图形中,找出一个性质与其他三个不同的来。
1.本文的开头有什么特点?
A 唯一的没有角的图形。
B 唯一的仅由直线构成的图形。
C 唯一的非对称性图形。
D 唯一由直线和曲线构成的图形。
结论:由于看图形的角度不同,四种答案全都正确。
即:事物的正确答案不止一个(提出论点)
说一说:这种开头方法有什么好处
新颖别致,使抽象的议论显得生动形象,通俗易懂,能引起读者的阅读兴趣。
不满足于一个答案,不放弃探求
这一点非常重要
“正确答案只有一个”这种思维模式,在我们头脑中已不知不觉地根深蒂固。这篇课文却提出相反观点,要求我们:
2.为什么说“事物的正确答案不止一个”?
由于背景的不同,考虑问题角度的变化,知识积累的差异等原因,事物的正确答案往往不止一个。
3.创造性思维有哪些必要的要素?
(1)有渊博的知识。
(2)有探求新事物,并为此而活用知识的态度和意识。
(3)有持之以恒的精神和毅力(不断地尝试)。
有渊博的知识 。
“这种情况可能出现在6分钟之后……”。“这种情况”指代什么?“它”指代什么?
“这种情况”指代“这些知识随时都可以进行组合,形成新的创意”。“它”指代“新的创意”。
有渊博的知识。
“我对此完全赞同”的“此”指什么?
富有创造力的人总是孜孜不倦地汲取知识,使自己学识渊博。
为什么“我对此完全赞同”?
因为“知识是形成新创意的素材”。
作者是如何来论证他的观点的?
举例论证
B.罗兰·布歇内尔把电视接收器作为试验对象,发明了交互式的乒乓球电子游戏,从此开始了游戏机的革命。
发挥创造力的真正关键,在于如何运用知识。
②有探求新事物并为此而活用知识的态度和意识。
A.谷登堡将葡萄压榨机和硬币打制器组合起来,发明了印刷机和排版术。
③有持之以恒的精神和毅力(不断地尝试)。
请补充一些例子来证明创造必须要有持之以恒的精神和毅力。
A.丁肇中在两年多的夜以继日的实验中发现了J粒子。
B.爱迪生用多种金属丝做实验,前后试过的材料不下1600种,终于发明了电灯。
C.居里夫人从几十吨的矿渣中提炼出不到1克的镭!
方法指导
补充论据
考点解说:
论据,是支撑论点的材料,是作者用来证明论点的理由和根据。根据论点补充论据,是近年来常见的题型,看起来要求比较宽泛,但补写的论据也要求典型,有代表性,说服力强。补写的论据不外乎两种形式:事实论据和道理论据。
考查方式:
你能否为要证明的论点再补充一个典型事例或一句名言警句?请选出最能证明论点的论据或请选出不能作为论据的一项。
方法点拨:
做这类题目,要注意以下两个方面:
1.看清楚要求补充的论据类型。
即看清楚要求补充的是名言还是事例;
2.补充名人事例要注意字数限制。
在日常学习生活中,我们可准备些关于“勤奋”“处世”“诚信”
“责任”“信念”等常见主题的名人事例和名言。名言的字数要少,事例要熟悉,不要为求新而准备那些较长的名言或不熟悉的名人事例。
补充原则:真实、典型,能够证明论点。
答题方式:人物+事例+简短评价。
4.是否拥有创造力的依据是什么?
不过,这种创造性的思维是否任何人都具备呢?是否存在富有创造力的人和缺乏创造力的人的区别呢?
由两个问句引出下文论述的具体内容。在结构上起承接、过渡作用。
不认为自己具有创造力
区分二者的根据之一是
拥有创造力的人留意自己细小的想法
区分一个人是否拥有创造力的主要依据:
富于创造力的人
缺乏创造力的人
认为自己具有创造力
结论:人人都具有创造力
1.有人说只有贝多芬、爱因斯坦以及莎士比亚才具备创造性思维,你同意这种观点吗?联系自己的生活经验谈谈你的看法。
合作探究
不同意。在大多数情况下,即便是他们,也并非轻而易举就能获得如此非凡的灵感。相反,这种非凡的灵感,往往产生于这样的过程:关注极其普通,甚至一闪念的想法,并对它反复推敲,逐渐充实。
我们每个人都有无限的潜能和创造力,而这个创造力可以无止境地运用于我们生活中的每个角落。我们最需要问自己的一个问题并非我们是否有创造力,而是如何能够发现并发挥他的潜能和创造力,这也是影响自身创造力是否发挥的根本。
示例:
2.怎样才能做一个富有创造力的人呢?
(1)要经常保持好奇心,不断积累知识。
(2)不满足于一个答案,而去探求新思路,去运用所获得的知识。
(3)一旦产生小的灵感,相信它的价值,并锲而不舍地把它发展下去。
3.你认为发挥创造力的关键是什么?
如何运用知识
首先坚信任何人都拥有创造力,留意自己细小的想法,小的创意会打开大的突破口,并坚信自己一定能使之变为现实。
主要论述怎样才能拥有创造力的问题。
关于创造性必需的三个要素,经过课文逐层论述,最后才给出答案,这合乎“分→总”这种思维规律,便于读者理解和把握。
4.本文主要论述了什么问题?关于创造性思维所必需的要素,为什么到篇末才给出全部答案?
①然而在大多数情况下,即便是他们,也并非轻而易举就能获得如此非凡的灵感。
5.赏析语言,说说下列句子中画横线的词语能否删去?为什么?
不能删去。“大多数”一词强调了获得灵感多数情况下并非轻而易举,但也有轻而易举获得灵感的时候。这一词语体现了议论文语言的严密性。
②富有创造力的人总是孜孜不倦地汲取知识,使自己学识渊博。
不能删去。“总是”强调了富有创造性的人能够长时间的、孜孜不倦地汲取知识,如果删去了就没有强调的意味,表示的范围也不明确。
③发挥创造力的真正关键,在于如何运用知识。
不能删去。“真正关键”强调了“如何运用知识”是发挥创造力的最重要的必需的要素,如果删去,则表明该要素是一般的, 无突出强调的效果。
④区分一个人是否拥有创造力,主要根据之一是,拥有创造力的人留意自己细小的想法。
不能删去。“之一”表示区分一个人是否具有创造力,除了这一根据之外,还有别的根据,如果删去,就显得太绝对,体现不了议论文语言的严密性。
本文由一个选择题入手,阐述什么是创造性思维,以及怎样才能成为一个有创造力的人,号召人们坚信自己的创造力,努力保持好奇心,不断探求,成为富有创造力的人。
概括主题
长期以来,人们习惯了“正确答案只有一个”的思维模式,其实在我们的生活中,很多事物的答案并不是唯一的。同一个事物,从不同的角度来观察,会得出不同的结论。生活是五彩缤纷的,我们要处处留心,关注细节,成为一个富有创造力的人。
学后感悟
课文先用四个图形提出一个题,引出“事物的正确答案不止一个”的观点。接着,作者从“事物的正确答案不止一个”,引申出了“不满足于一个答案,不放弃探求,这一点非常重要”。既然不满足于一个答案,就需要寻求其他答案,那么怎样寻求呢?于是课文顺理成章地提出“有赖于创造性的思维”。紧接着,又引申出如下问题:“不过,这种创造性的思维是否任何人都具备呢?是否存在富有创造力的人和缺乏创造力的人的区别呢?”接下来的论述就是回答这个问题的。最后,课文得出结论:“任何人都拥有创造力”。只要具备几个关键性的要素,就能成为一个富有创造力的人。
围绕中心,逐层论述。
写作特色
例如:“若是某种数学问题的话,说正确答案只有一个是对的。”在此强调数学问题,这种用语是非常准确、严密的。因为数学问题的答案,一就是一,二就是二,思维的方式可以多样,但问题的答案只有一个。
语言准确、严密。
1.数学问题→生活问题:“事物的正确答案不止一个”
2.探求第二种答案有赖于创造性思维。
3. 任何人都拥有创造力,关键要具备三个要素。
必需要素
区分根据
a. 渊博的知识
b. 活用知识的态度和意识
c. 持之以恒的毅力
a.缺乏的人:自我压制
b.拥有的人:留意细小的想法,并相信自己
谈创造性思维
板书设计
A. 孜孜不倦(勤勉) 汲取(吸)
B. 持之以恒(恒心) 素材(材料)
C. 不言而喻(明白) 创意(创造性)
D. 锲而不舍(雕刻) 根深蒂固(花或瓜果与枝茎相连的部分)
1. 下列画线词语解释有误的一项是( )
【解析】“素”的意思是未经提炼和加工的;原始的。
B
课堂练习
(1)富有创造力的人总是孜孜不倦地 (汲取 学习)知识,使自己 (学识 学问)渊博。
(2)知识是形成新创意的 (材料 素材)。 但这并不是说,光凭知识就能拥有 (创造性 创造力)。
2.选词填空。
汲取
学识
素材
创造力
3.同一个问题,从不同的角度分析,可以得出不同的结论,正如罗迦·费·因格所说的“事物的正确答案不止一个”请你以不同角度从《龟兔赛跑》的故事中提炼观点(至少两个)。
示例:
1.万物没有绝对的
2.只要努力就有可能
B
课后练习
A
B
不能。如果把“主要”和“之一”去掉,就变成了“留意自己细小的想法”是拥有创造力的唯一根据,这与事实不符;这两个词很好地体现了议论文语言的准确性。
“并非轻而易举”体现了议论文语言的准确性、严密性,它准确地说明了灵感的产生是积累、活用知识的产物。
示例:说明了国家重视科技创新,全社会积极创新。
示例一:第一幅更好。第一幅图简洁明了,要素是“创”字和两只手,意思是用双手创造。双手造型像展开的双翼,寓意是“创客很棒”,比喻进步腾飞。示例二:第二幅更好。第二幅图上有许多人,年龄、性别、身份不同,表示大众创业、万众创新;上面有灯光,表明创新、创造给人们的生活带来光明,照亮每个人的未来。这幅图寓意更深刻,引人沉思。
想一想:
玩24点扑克牌的游戏:用5、6、
3、3、四 张牌通过加减乘除的运算得
出24这个结果, 每张牌只能用一次。
考考你
发挥想象,下面的图形会是什么
关于小鸡过马路的话题
拿破仑:不想过马路的鸡不是好鸡。
爱因斯坦:小鸡的成功=勇敢的穿越+正确的方法+少说空话。
达尔文:鸡从森林来到人家再发展到马路,这是优胜劣汰的进化法则。
阿基米德:只要给我一条马路,我就能让小鸡走过去。
同课章节目录
- 第一单元
- 1 沁园春·雪
- 2 我爱这土地
- 3 乡愁(余光中)
- 4 你是人间的四月天
- 5 我看
- 任务二 自由朗诵
- 任务三 尝试创作
- 名著导读(一)《艾青诗选》:如何读诗
- 第二单元
- 6 敬业与乐业
- 7 就英法联军远征中国致巴特勒上尉的信
- 8* 论教养
- 9* 精神的三间小屋
- 写作 观点要明确
- 第三单元
- 10 岳阳楼记
- 11 醉翁亭记
- 12* 湖心亭看雪
- 13 诗词三首
- 写作 议论要言之有据
- 课外古诗词诵读(一)
- 第四单元
- 14 故乡
- 15 我的叔叔于勒
- 16* 孤独之旅
- 写作 学习缩写
- 第五单元
- 17 中国人失掉自信力了吗
- 18 怀疑与学问
- 19 谈创造性思维
- 20* 创造宣言
- 写作 论证要合理
- 口语交际 讨论
- 第六单元
- 21 智取生辰纲
- 22 范进中举
- 23* 三顾茅庐
- 24* 刘姥姥进大观园
- 写作 学习改写
- 名著导读(二) 《水浒传》:古典小说的阅读
- 课外古诗词诵读(二)
