等腰三角形的复习课[上学期]
文档属性
| 名称 | 等腰三角形的复习课[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 870.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-11-19 00:00:00 | ||
图片预览



文档简介
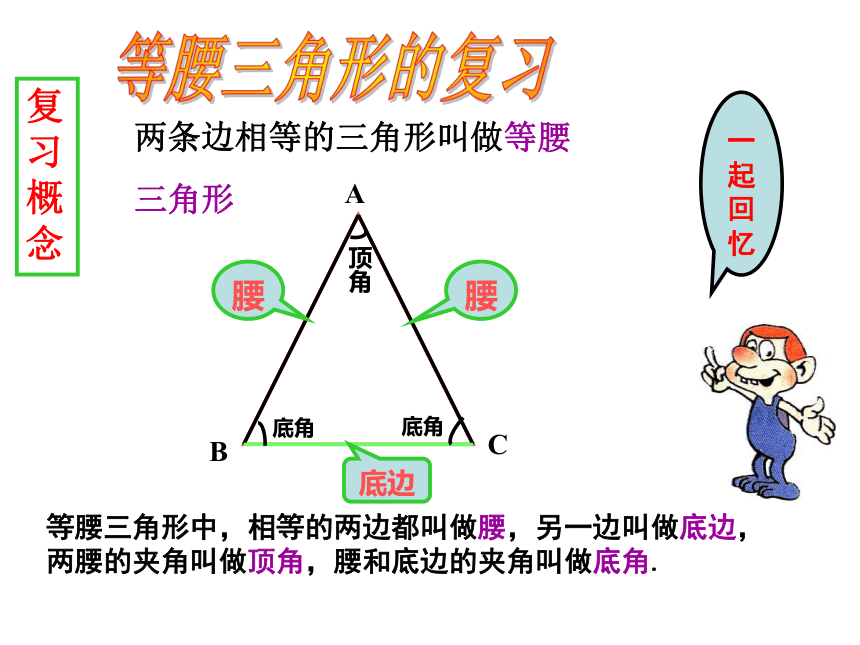
课件18张PPT。等腰三角形的复习课温中实验学校 钟凌峰等腰三角形的复习两条边相等的三角形叫做等腰
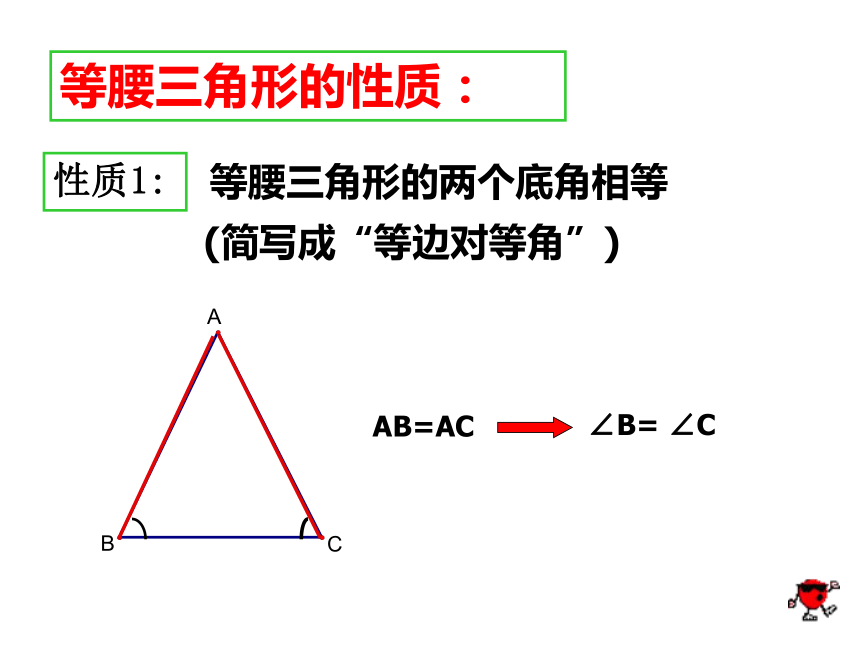
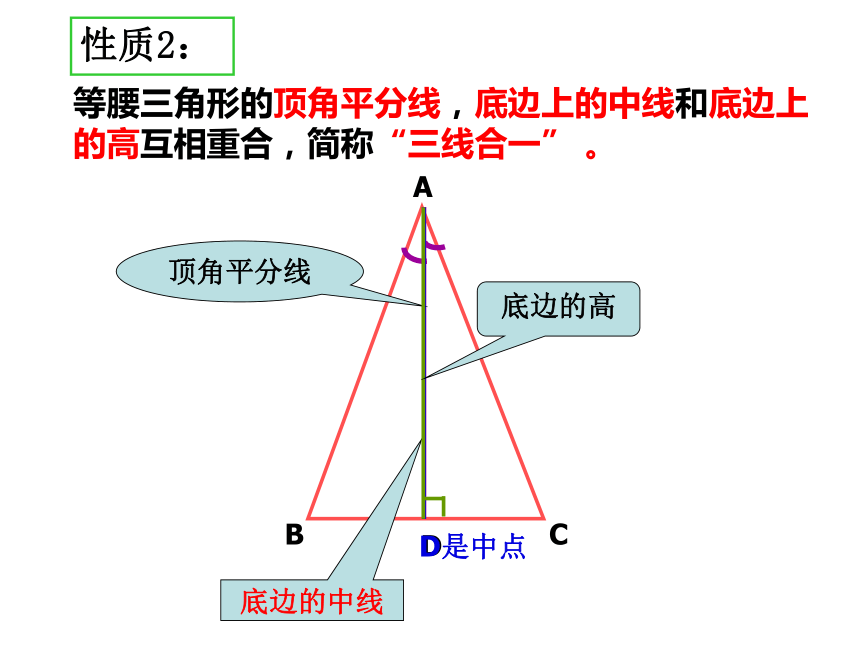
三角形 等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.底边一起回忆复习概念性质1:等腰三角形的性质:等腰三角形的两个底角相等(简写成“等边对等角”)AB=AC ∠B= ∠C性质2:等腰三角形的顶角平分线,底边上的中线和底边上的高互相重合,简称“三线合一” 。在同一个三角形中,有两条边相等。(利用定义)等腰三角形的识别:如果一个三角形中有两个角相等,那么这两个角所对的边也相等,(简写成“等角对等边”)
(1)如果等腰三角形的一个底角为50°,
那么其余两个角为_____和_____.
(2)如果等腰三角形的顶角为80°,
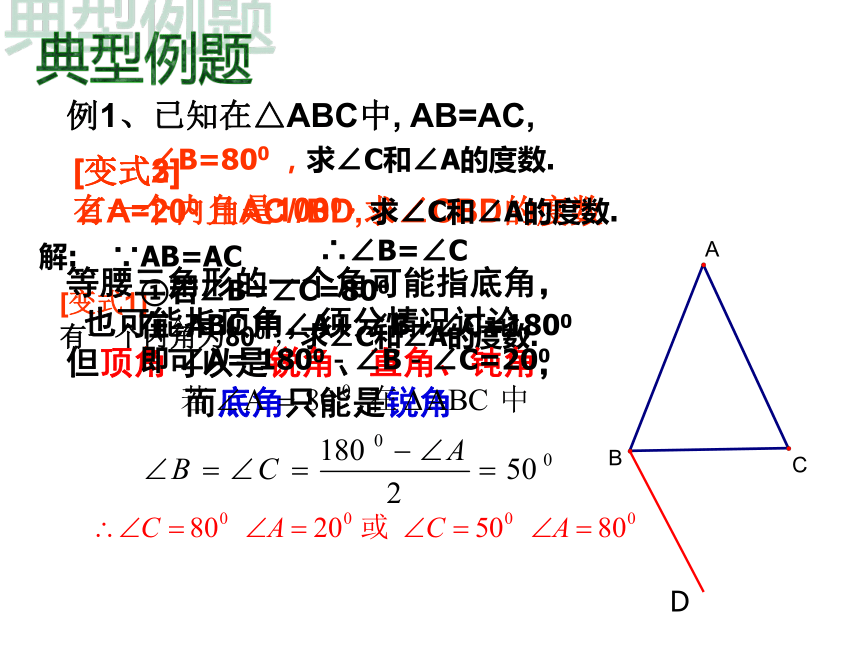
那么它的一个底角为______. 80° 50° 50° 先热身,比一比谁更快!练习:例1、已知在△ABC中, AB=AC, [变式3] ∠A=200 且AC//BD,求∠CBD的度数[变式1] 有一个内角为800 ,求∠C和∠A的度数. [变式2] 有一个内角是1000 ,求∠C和∠A的度数. 典型例题∠B=800 ,求∠C和∠A的度数.等腰三角形的一个角可能指底角,也可能指顶角,须分情况讨论,但顶角可以是锐角、直角、钝角,而底角只能是锐角
解: ∵AB=AC∴∠B=∠C①若∠B=∠C=800
在△ABC 中∠A+ ∠B+∠C=1800
即 ∠A= 1800-∠B-∠C=200 例2、 如图:△ABC中,D是AC上的一点,且AD=DB=BC,∠DBC=20°,试求∠A的度数。
变式练习:如果AB=AC,AD=DB=BC,求∠A的度数。典型例题AB=AC例3:已知在△ABC中, AB=AC, BE、CD分别平分 ∠ABC、 ∠ACB,且相交于点O,
试说明△BOC是等腰三角形。外角的角平分线典型例题1212ODEODE 在△ABC中,已知 , BO平分∠ABC,CO平分∠ACB.(1)请问图中有多少个等腰三角形?说明理由。(2)线段EF和线段EB,FC之间有没有关系? 若有是什么关系?你会吗AB=ACAB≠ACEF过点O作直线EF//BC 交 AB 于 E,交 AC 于 F。(1)五个,分别是△ABC、 △OBC、 △AEF、 △EOB、 △FOC(2)EF=2EB=2CF:EF=EB+FC 如图在△ABC中,∠ABC=∠ACB,BO平分∠ABC,CO平分∠ACB,由这两个已知条件,自己能导出什么结论?ABCO∠OBC=∠OCB , OB=OC在这张图上,过O作一直线EF和边BC平行,与AB交于E,与AC交于F.请同学们考虑:EF12345(1)仔细寻找一下,这张图中有几个等腰三角形?为什么?
(2)添上去的这条线段和线段BE、CF之间有没有关系?有的话,是怎样一种关系?(1)五个,分别是△ABC、 △OBC、 △AEF、 △EOB、 △FOC(2)EF=2EB=2CF:EF=EB+FCABDEC1.在△ABC中,AB=AC,D是AC上的一点,使BD=BC,
E是AB上一点使AD=DE=BE,则∠A=2、如图:△ABC中,AB=AC,BD=CE 求证:∠1=∠2方法一:BD=CE
∠B=∠C
AB=AC△ABD≌ △ACE AD=AE ∠1=∠2ABCDE12△ABD≌ △ACE ∠ADB=∠AEC ∠1=∠2方法三:BE=CD
∠B=∠C
AB=AC△ABE≌△ACD ∠1=∠2AB=AC
AB=AC
BD=CE方法二:3、如图:已知D、E在BC上,AB=AC,
AD=AE
求证:BD=CE ABDEC考考你: 1、如果一个等腰三角形一腰上的高与另一腰的
夹角为40度,那么它的底角为 。 2、等腰三角形底边长为5厘米,一腰上的中线把
其周长分为两部分之差为2厘米,则腰长为 . 25°或 65°7cm或3cm3、等腰三角形一腰上的中线把其周长分为12厘米和9厘米两部分,则腰长为 . 8cm或6cm4、等腰三角形一腰上的中线把其周长分为12厘米和6厘米两部分,则腰长为 . 8cmAFCDBE1、如图,AD是△ABC中∠BAC的平分线,E是AB上
的一点,AE=AC,EF∥BC交AC于点F,
求证;CE平分∠DEF想一想2、如图,在△ABC中,AB=AC,点E在AB上,
点D在AC的
延长线上,DC=EB,ED交BC于M。
求证:EM=DMA BCDEM小结:一、在等腰三角形中求角在具体计算时利用: ① 等边对等角
② 三角形的内角和
③ 三角形的外角的性质二、等腰三角形的识别方法:①两边相等(定义)
②在同一个三角形中,有两个角相等注:说明两角相等的途径: ①等边对等角
②在两条平行线中的同位角,内错角。
③角平分线的定义 。 ④利用等量代换。
三、数学思想: ①分类讨论的思想 ② 转化的思想祝同学们
学习进步再见
三角形 等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.底边一起回忆复习概念性质1:等腰三角形的性质:等腰三角形的两个底角相等(简写成“等边对等角”)AB=AC ∠B= ∠C性质2:等腰三角形的顶角平分线,底边上的中线和底边上的高互相重合,简称“三线合一” 。在同一个三角形中,有两条边相等。(利用定义)等腰三角形的识别:如果一个三角形中有两个角相等,那么这两个角所对的边也相等,(简写成“等角对等边”)
(1)如果等腰三角形的一个底角为50°,
那么其余两个角为_____和_____.
(2)如果等腰三角形的顶角为80°,
那么它的一个底角为______. 80° 50° 50° 先热身,比一比谁更快!练习:例1、已知在△ABC中, AB=AC, [变式3] ∠A=200 且AC//BD,求∠CBD的度数[变式1] 有一个内角为800 ,求∠C和∠A的度数. [变式2] 有一个内角是1000 ,求∠C和∠A的度数. 典型例题∠B=800 ,求∠C和∠A的度数.等腰三角形的一个角可能指底角,也可能指顶角,须分情况讨论,但顶角可以是锐角、直角、钝角,而底角只能是锐角
解: ∵AB=AC∴∠B=∠C①若∠B=∠C=800
在△ABC 中∠A+ ∠B+∠C=1800
即 ∠A= 1800-∠B-∠C=200 例2、 如图:△ABC中,D是AC上的一点,且AD=DB=BC,∠DBC=20°,试求∠A的度数。
变式练习:如果AB=AC,AD=DB=BC,求∠A的度数。典型例题AB=AC例3:已知在△ABC中, AB=AC, BE、CD分别平分 ∠ABC、 ∠ACB,且相交于点O,
试说明△BOC是等腰三角形。外角的角平分线典型例题1212ODEODE 在△ABC中,已知 , BO平分∠ABC,CO平分∠ACB.(1)请问图中有多少个等腰三角形?说明理由。(2)线段EF和线段EB,FC之间有没有关系? 若有是什么关系?你会吗AB=ACAB≠ACEF过点O作直线EF//BC 交 AB 于 E,交 AC 于 F。(1)五个,分别是△ABC、 △OBC、 △AEF、 △EOB、 △FOC(2)EF=2EB=2CF:EF=EB+FC 如图在△ABC中,∠ABC=∠ACB,BO平分∠ABC,CO平分∠ACB,由这两个已知条件,自己能导出什么结论?ABCO∠OBC=∠OCB , OB=OC在这张图上,过O作一直线EF和边BC平行,与AB交于E,与AC交于F.请同学们考虑:EF12345(1)仔细寻找一下,这张图中有几个等腰三角形?为什么?
(2)添上去的这条线段和线段BE、CF之间有没有关系?有的话,是怎样一种关系?(1)五个,分别是△ABC、 △OBC、 △AEF、 △EOB、 △FOC(2)EF=2EB=2CF:EF=EB+FCABDEC1.在△ABC中,AB=AC,D是AC上的一点,使BD=BC,
E是AB上一点使AD=DE=BE,则∠A=2、如图:△ABC中,AB=AC,BD=CE 求证:∠1=∠2方法一:BD=CE
∠B=∠C
AB=AC△ABD≌ △ACE AD=AE ∠1=∠2ABCDE12△ABD≌ △ACE ∠ADB=∠AEC ∠1=∠2方法三:BE=CD
∠B=∠C
AB=AC△ABE≌△ACD ∠1=∠2AB=AC
AB=AC
BD=CE方法二:3、如图:已知D、E在BC上,AB=AC,
AD=AE
求证:BD=CE ABDEC考考你: 1、如果一个等腰三角形一腰上的高与另一腰的
夹角为40度,那么它的底角为 。 2、等腰三角形底边长为5厘米,一腰上的中线把
其周长分为两部分之差为2厘米,则腰长为 . 25°或 65°7cm或3cm3、等腰三角形一腰上的中线把其周长分为12厘米和9厘米两部分,则腰长为 . 8cm或6cm4、等腰三角形一腰上的中线把其周长分为12厘米和6厘米两部分,则腰长为 . 8cmAFCDBE1、如图,AD是△ABC中∠BAC的平分线,E是AB上
的一点,AE=AC,EF∥BC交AC于点F,
求证;CE平分∠DEF想一想2、如图,在△ABC中,AB=AC,点E在AB上,
点D在AC的
延长线上,DC=EB,ED交BC于M。
求证:EM=DMA BCDEM小结:一、在等腰三角形中求角在具体计算时利用: ① 等边对等角
② 三角形的内角和
③ 三角形的外角的性质二、等腰三角形的识别方法:①两边相等(定义)
②在同一个三角形中,有两个角相等注:说明两角相等的途径: ①等边对等角
②在两条平行线中的同位角,内错角。
③角平分线的定义 。 ④利用等量代换。
三、数学思想: ①分类讨论的思想 ② 转化的思想祝同学们
学习进步再见
