等腰三角形的性质[上学期]
文档属性
| 名称 | 等腰三角形的性质[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 228.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-12-20 10:42:00 | ||
图片预览






文档简介
课件18张PPT。等腰三角形的性质高青县实验中学 李冰等腰三角形的性质
知识讲解
课堂练习
课堂小结
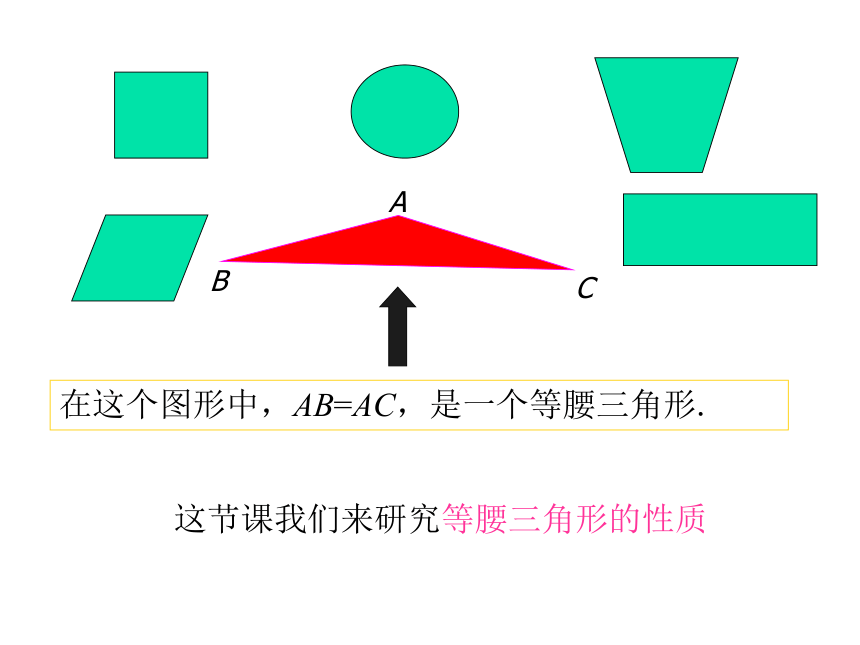
观察下列图片,找出你所熟悉的几何图形课题引入在这个图形中,AB=AC,是一个等腰三角形.ABC这节课我们来研究等腰三角形的性质观察与思考 等腰三角形不同与一般的三角形,它的各元素之间有什么更特殊或独特的性质?我们该从哪些方面去考虑?两个底角相等;
两个腰相等;
两个腰上的角平分线相等;
两个腰上的高相等;
两个腰上的中线相等. 通过观察、测量,你发现等腰三角形的边、角、线等各元素之间有什么特殊的性质? 已知:△ABC中,AB=AC
求证:∠B=∠CABC分析: 要证明两个角相等,根据已知条件需要构造两个全等的三角形. 已知:△ABC中,AB=AC
求证:∠B=∠CABCD证明:作顶角的平分线AD在△BAD和△CAD中AB=AC(已知)∠BAD=∠CAD(辅助线做法)AD=AD(公共边)∴△BAD≌△CAD(SAS)∴∠B=∠C(全等三角形的对应角相等)思考:1、有无其他方法来构造两个全等的三角形?
2、为什么顶角的角平分线、底边上的高和中线重合
在一起?
3、等边三角形的三个内角有何关系?为什么?等腰三角形的性质定理等腰三角形的两个底角相等(等边对等角)
ABC12AC=BC∠1=∠2小结等腰三角形的性质定理推论1 等腰三角形顶角平分线平分底边
并且垂直于底边.AD=BD∠ADC=∠BDC
DC⊥AB
AC=BC等腰三角形的性质定理推论2
等边三角形的各角都相等,并且每一个角都等于60度.CABAC=CB=BA∠A=∠B=∠C=600例1已知:房屋的顶角∠BAC=1000, 过屋顶A的立柱AD⊥BC,屋椽AB=AC. 求顶架上∠B、∠C、∠BAD、∠CAD的度数.解:在△ABC中,
∵AB=AC(已知)
∴∠B=∠C(等边对等角)
∴∠B=∠C=(1800-∠A)=400(三角形内角和定理).
又∵AD⊥BC(已知),
∴∠BAD=∠CAD(等腰三角形的平分线与底边上的高互相重合)
∴∠BAD=∠CAD=500题组训练一、填空题
1.在△ABC中,AB=AC,若顶角为80°,则底角的外角为_________.
2.在△ABC中,若AB=AC,∠B=∠A,则∠C=_____________.
3.在△ABC中,若AB=AC,∠B的余角为25°,则∠A=____________.
课后练习已知:如下图,在△ABC中,D是AB边
上的一点,AD=DC,∠B=35°,
∠ACD=43° 求:∠BCD的度数
ADC 本节学习了等腰三角形的性质定理和两个推论,还通过例题学习了如何分析几何证题的思路.
课堂小结再见
知识讲解
课堂练习
课堂小结
观察下列图片,找出你所熟悉的几何图形课题引入在这个图形中,AB=AC,是一个等腰三角形.ABC这节课我们来研究等腰三角形的性质观察与思考 等腰三角形不同与一般的三角形,它的各元素之间有什么更特殊或独特的性质?我们该从哪些方面去考虑?两个底角相等;
两个腰相等;
两个腰上的角平分线相等;
两个腰上的高相等;
两个腰上的中线相等. 通过观察、测量,你发现等腰三角形的边、角、线等各元素之间有什么特殊的性质? 已知:△ABC中,AB=AC
求证:∠B=∠CABC分析: 要证明两个角相等,根据已知条件需要构造两个全等的三角形. 已知:△ABC中,AB=AC
求证:∠B=∠CABCD证明:作顶角的平分线AD在△BAD和△CAD中AB=AC(已知)∠BAD=∠CAD(辅助线做法)AD=AD(公共边)∴△BAD≌△CAD(SAS)∴∠B=∠C(全等三角形的对应角相等)思考:1、有无其他方法来构造两个全等的三角形?
2、为什么顶角的角平分线、底边上的高和中线重合
在一起?
3、等边三角形的三个内角有何关系?为什么?等腰三角形的性质定理等腰三角形的两个底角相等(等边对等角)
ABC12AC=BC∠1=∠2小结等腰三角形的性质定理推论1 等腰三角形顶角平分线平分底边
并且垂直于底边.AD=BD∠ADC=∠BDC
DC⊥AB
AC=BC等腰三角形的性质定理推论2
等边三角形的各角都相等,并且每一个角都等于60度.CABAC=CB=BA∠A=∠B=∠C=600例1已知:房屋的顶角∠BAC=1000, 过屋顶A的立柱AD⊥BC,屋椽AB=AC. 求顶架上∠B、∠C、∠BAD、∠CAD的度数.解:在△ABC中,
∵AB=AC(已知)
∴∠B=∠C(等边对等角)
∴∠B=∠C=(1800-∠A)=400(三角形内角和定理).
又∵AD⊥BC(已知),
∴∠BAD=∠CAD(等腰三角形的平分线与底边上的高互相重合)
∴∠BAD=∠CAD=500题组训练一、填空题
1.在△ABC中,AB=AC,若顶角为80°,则底角的外角为_________.
2.在△ABC中,若AB=AC,∠B=∠A,则∠C=_____________.
3.在△ABC中,若AB=AC,∠B的余角为25°,则∠A=____________.
课后练习已知:如下图,在△ABC中,D是AB边
上的一点,AD=DC,∠B=35°,
∠ACD=43° 求:∠BCD的度数
ADC 本节学习了等腰三角形的性质定理和两个推论,还通过例题学习了如何分析几何证题的思路.
课堂小结再见
