14.3.1等腰三角形[上学期]
文档属性
| 名称 | 14.3.1等腰三角形[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 107.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-01-19 11:45:00 | ||
图片预览




文档简介
课件18张PPT。14.3.1
等腰三角形学习目标:
1、理解等腰三角形的有关概念
2、掌握等边对等角和等腰三角形三线合一的性质自学指导
阅读课文:140页到142页
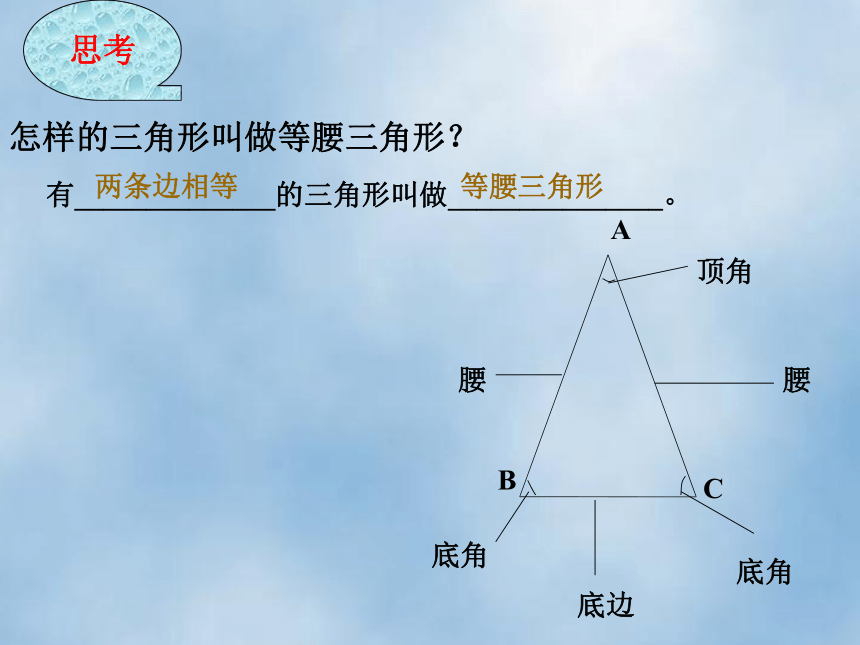
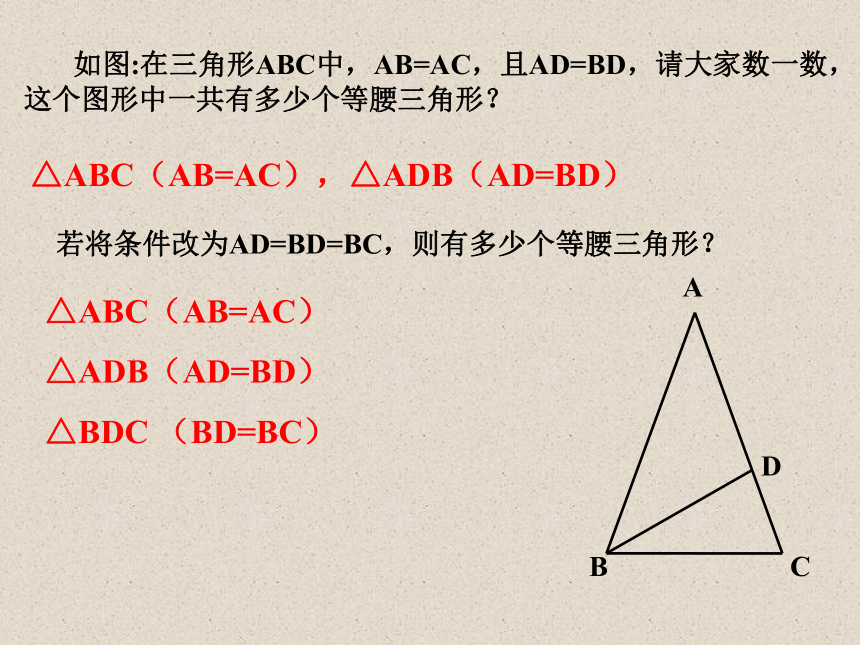
自学要求:理解等腰三角形定义,掌握等腰三角形两个性质定理。怎样的三角形叫做等腰三角形?有______________的三角形叫做_______________。思考两条边相等等腰三角形 如图:在三角形ABC中,AB=AC,且AD=BD,请大家数一数,这个图形中一共有多少个等腰三角形?△ABC(AB=AC),△ADB(AD=BD)若将条件改为AD=BD=BC,则有多少个等腰三角形?△ABC(AB=AC)
△ADB(AD=BD)
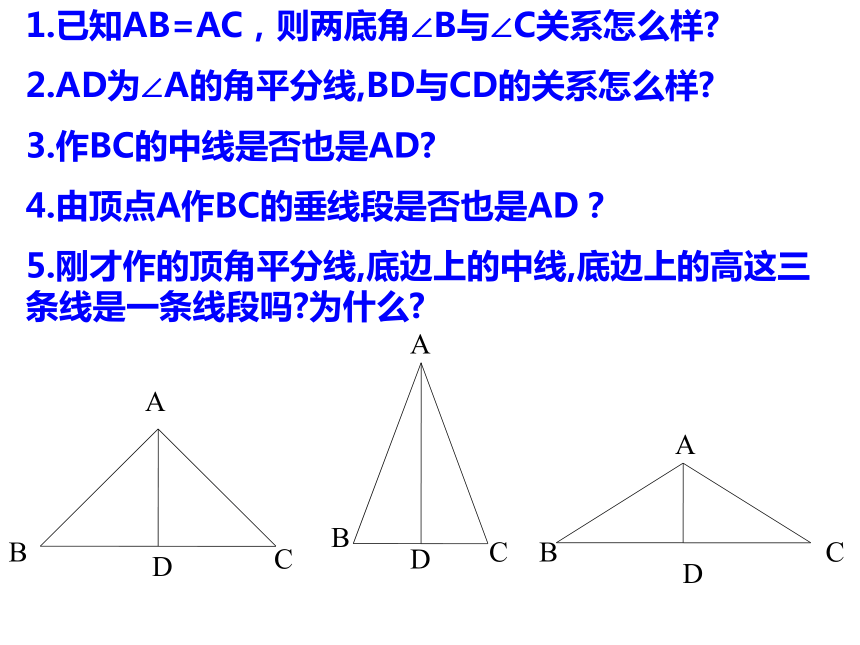
△BDC (BD=BC)1.已知AB=AC,则两底角∠B与∠C关系怎么样?
2.AD为∠A的角平分线,BD与CD的关系怎么样?
3.作BC的中线是否也是AD?
4.由顶点A作BC的垂线段是否也是AD?
5.刚才作的顶角平分线,底边上的中线,底边上的高这三条线是一条线段吗?为什么? 等腰三角形的性质
1 等腰三角形的两个底角相等(等边对等角)
2等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)例1 在三角形ABC中,已知AB=AC,且
∠B=80° ,则∠C=——度,∠A=——度?∵AB=AC(已知)
∴∠B=∠C(等边对等角)
∵∠B=80° (已知)
∴∠C=80°
又∵∠A+∠B+∠C=180° (三角形内角和为180° )
∴∠A=180°- ∠B-∠C
∠A=20°等腰三角形的性质
1 等腰三角形的两个底角相等(等边对等角)
2等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)
操练1 在三角形ABC中,已知AB=AC,且
∠ A=50° ,则∠B=——度,∠C=——度?∵AB=AC(已知)
∴∠B=∠C(等边对等角)又∵∠A+∠B+∠C=180° (三角形内角和为180° )
∠A=50° (已知)
∴∠B=65°
∠C=65°
等腰三角形的性质
1 等腰三角形的两个底角相等(等边对等角)
2等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)
操练2 在等腰三角形ABC中,如果AB=AC,且一个角等于70° ,求另两个角的度数。若顶角即∠A=70° 则∠B=55 ° ∠C=55 °
若底角即∠B=70° 则∠C=70° ∠A=40°
若底角即∠C=70° 则∠B=70° ∠A=40°在等腰三角形中,我们只要知道任一个角,就可以求出另外两个角!若改为90°呢?例1 如图:在△ABC中,AB=AC,点D在AC上,且BC=AD=BD,求△ABC各角的度数。解:∵AB=AC,BC=AD=BD)∴∠ABC=∠C=∠BDC
∠A=∠ABD (等边对等角)设∠A=x,则∠BDC=∠A+∠ABD=2X从而∠ABC=∠C=∠BDC=2X于是在△ABC中,有
∠A+∠ABC+∠C=X+2X+2X=1800解得 X=360在△ABC中,∠A=360,∠ABC=∠C=720趣味数学: 如图:点B、C、D、E、F在∠MAN的边上, ∠A=15°,AB=BC=CD=DE=EF,求∠ MEF的度数。 已知在等腰三角形ABC中,A=36° ,B=72° ,C=72° ,请同学们想一想,如何添一条线,将等腰三角形ABC分成两个等腰三角形?成功后,如何再添一条线,多得到一个等腰三角形?还可以继续吗?只要将做∠ B的角平分线即可!
只要再做∠ BDE的角平分线即可!
以下步骤重复下去即可!
等腰三角形的性质
1 等腰三角形的两个底角相等(等边对等角)
2等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)
例2 在三角形ABC中,AB=AC,且AD ⊥BC,已知BD=2cm,求DC=___cm, BC=___cm?∵AD ⊥BC(已知)
∴BD=CD(等腰三角形的高与底边上的中线重合)
即(等腰三角形三线
合一)
∵BD=2cm(已知)
∴CD=2cm等腰三角形的性质
1 等腰三角形的两个底角相等(等边对等角)
2等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)
例3 在三角形ABC中,AB=AC,且AD ⊥BC,已知∠ 1=20°,求∠ 2=_____度∠ A=______度?∵AD ⊥BC(已知)
∴ ∠ 1= ∠ 2 (等腰三角形的高与顶角的平分线重合)
即(等腰三角形三线
合一)
∵ ∠ 1=20° (已知)
∴ ∠ A=40°等腰三角形的性质
1 等腰三角形的两个底角相等(等边对等角)
2等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)操练3 在三角形ABC中,AB=AC=5cm,AD=4cm,且BD=CD,求点A到线段BC的距离。∵AB=AC(已知)
∴△ABC是等腰三角形
∵BD=CD(已知)
∴BD⊥CD(等腰三角形三线合一)
∴线段AD的长度
就是点A
到线段BC的距离
即为4 cm等腰三角形的性质
1 等腰三角形的两个底角相等(等边对等角)
2等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)例4已知AD⊥ BC,试找出等腰三角形ABC (AB=AC)中,存在相等关系的量。∠B=∠C
∠1=∠2
∠BDA=∠CDA=90°
BD=CD等腰三角形的性质
1 等腰三角形的两个底角相等(等边对等角)
2等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)一休学数学
在三角形ABC中,已知AB=AC,且
要证∠1=∠2,如何去证?
这道题因被墨水遮去了
一个条件,一休无从下手,
现在请同学们帮一休补
上这个条件,使一休
能做出这道题。怎么办?小结:
本堂课主要学习了等腰三角形的两个性质:即等边对等角和等腰三角形三线合一。
只要知道等腰三角形的一个角的度数,我们就可以求出另外两个角的度数!
只要知道等腰三角形底边上的中线,底边上的高,顶角的平分线中任一个条件,我们就可以知道另外两个条件!作业:149页
第1、2、3题
等腰三角形学习目标:
1、理解等腰三角形的有关概念
2、掌握等边对等角和等腰三角形三线合一的性质自学指导
阅读课文:140页到142页
自学要求:理解等腰三角形定义,掌握等腰三角形两个性质定理。怎样的三角形叫做等腰三角形?有______________的三角形叫做_______________。思考两条边相等等腰三角形 如图:在三角形ABC中,AB=AC,且AD=BD,请大家数一数,这个图形中一共有多少个等腰三角形?△ABC(AB=AC),△ADB(AD=BD)若将条件改为AD=BD=BC,则有多少个等腰三角形?△ABC(AB=AC)
△ADB(AD=BD)
△BDC (BD=BC)1.已知AB=AC,则两底角∠B与∠C关系怎么样?
2.AD为∠A的角平分线,BD与CD的关系怎么样?
3.作BC的中线是否也是AD?
4.由顶点A作BC的垂线段是否也是AD?
5.刚才作的顶角平分线,底边上的中线,底边上的高这三条线是一条线段吗?为什么? 等腰三角形的性质
1 等腰三角形的两个底角相等(等边对等角)
2等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)例1 在三角形ABC中,已知AB=AC,且
∠B=80° ,则∠C=——度,∠A=——度?∵AB=AC(已知)
∴∠B=∠C(等边对等角)
∵∠B=80° (已知)
∴∠C=80°
又∵∠A+∠B+∠C=180° (三角形内角和为180° )
∴∠A=180°- ∠B-∠C
∠A=20°等腰三角形的性质
1 等腰三角形的两个底角相等(等边对等角)
2等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)
操练1 在三角形ABC中,已知AB=AC,且
∠ A=50° ,则∠B=——度,∠C=——度?∵AB=AC(已知)
∴∠B=∠C(等边对等角)又∵∠A+∠B+∠C=180° (三角形内角和为180° )
∠A=50° (已知)
∴∠B=65°
∠C=65°
等腰三角形的性质
1 等腰三角形的两个底角相等(等边对等角)
2等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)
操练2 在等腰三角形ABC中,如果AB=AC,且一个角等于70° ,求另两个角的度数。若顶角即∠A=70° 则∠B=55 ° ∠C=55 °
若底角即∠B=70° 则∠C=70° ∠A=40°
若底角即∠C=70° 则∠B=70° ∠A=40°在等腰三角形中,我们只要知道任一个角,就可以求出另外两个角!若改为90°呢?例1 如图:在△ABC中,AB=AC,点D在AC上,且BC=AD=BD,求△ABC各角的度数。解:∵AB=AC,BC=AD=BD)∴∠ABC=∠C=∠BDC
∠A=∠ABD (等边对等角)设∠A=x,则∠BDC=∠A+∠ABD=2X从而∠ABC=∠C=∠BDC=2X于是在△ABC中,有
∠A+∠ABC+∠C=X+2X+2X=1800解得 X=360在△ABC中,∠A=360,∠ABC=∠C=720趣味数学: 如图:点B、C、D、E、F在∠MAN的边上, ∠A=15°,AB=BC=CD=DE=EF,求∠ MEF的度数。 已知在等腰三角形ABC中,A=36° ,B=72° ,C=72° ,请同学们想一想,如何添一条线,将等腰三角形ABC分成两个等腰三角形?成功后,如何再添一条线,多得到一个等腰三角形?还可以继续吗?只要将做∠ B的角平分线即可!
只要再做∠ BDE的角平分线即可!
以下步骤重复下去即可!
等腰三角形的性质
1 等腰三角形的两个底角相等(等边对等角)
2等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)
例2 在三角形ABC中,AB=AC,且AD ⊥BC,已知BD=2cm,求DC=___cm, BC=___cm?∵AD ⊥BC(已知)
∴BD=CD(等腰三角形的高与底边上的中线重合)
即(等腰三角形三线
合一)
∵BD=2cm(已知)
∴CD=2cm等腰三角形的性质
1 等腰三角形的两个底角相等(等边对等角)
2等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)
例3 在三角形ABC中,AB=AC,且AD ⊥BC,已知∠ 1=20°,求∠ 2=_____度∠ A=______度?∵AD ⊥BC(已知)
∴ ∠ 1= ∠ 2 (等腰三角形的高与顶角的平分线重合)
即(等腰三角形三线
合一)
∵ ∠ 1=20° (已知)
∴ ∠ A=40°等腰三角形的性质
1 等腰三角形的两个底角相等(等边对等角)
2等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)操练3 在三角形ABC中,AB=AC=5cm,AD=4cm,且BD=CD,求点A到线段BC的距离。∵AB=AC(已知)
∴△ABC是等腰三角形
∵BD=CD(已知)
∴BD⊥CD(等腰三角形三线合一)
∴线段AD的长度
就是点A
到线段BC的距离
即为4 cm等腰三角形的性质
1 等腰三角形的两个底角相等(等边对等角)
2等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)例4已知AD⊥ BC,试找出等腰三角形ABC (AB=AC)中,存在相等关系的量。∠B=∠C
∠1=∠2
∠BDA=∠CDA=90°
BD=CD等腰三角形的性质
1 等腰三角形的两个底角相等(等边对等角)
2等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)一休学数学
在三角形ABC中,已知AB=AC,且
要证∠1=∠2,如何去证?
这道题因被墨水遮去了
一个条件,一休无从下手,
现在请同学们帮一休补
上这个条件,使一休
能做出这道题。怎么办?小结:
本堂课主要学习了等腰三角形的两个性质:即等边对等角和等腰三角形三线合一。
只要知道等腰三角形的一个角的度数,我们就可以求出另外两个角的度数!
只要知道等腰三角形底边上的中线,底边上的高,顶角的平分线中任一个条件,我们就可以知道另外两个条件!作业:149页
第1、2、3题
