北师大版九年级数学上册试题第六章 反比例函数 单元测试卷(含答案)
文档属性
| 名称 | 北师大版九年级数学上册试题第六章 反比例函数 单元测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 873.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-20 08:28:35 | ||
图片预览

文档简介
第六章 《反比例函数》单元测试卷
一、选择题:本题共12个小题,每小题3分,共36分。在每小题给出的四个选项中,只有一项是符合题目要求的。
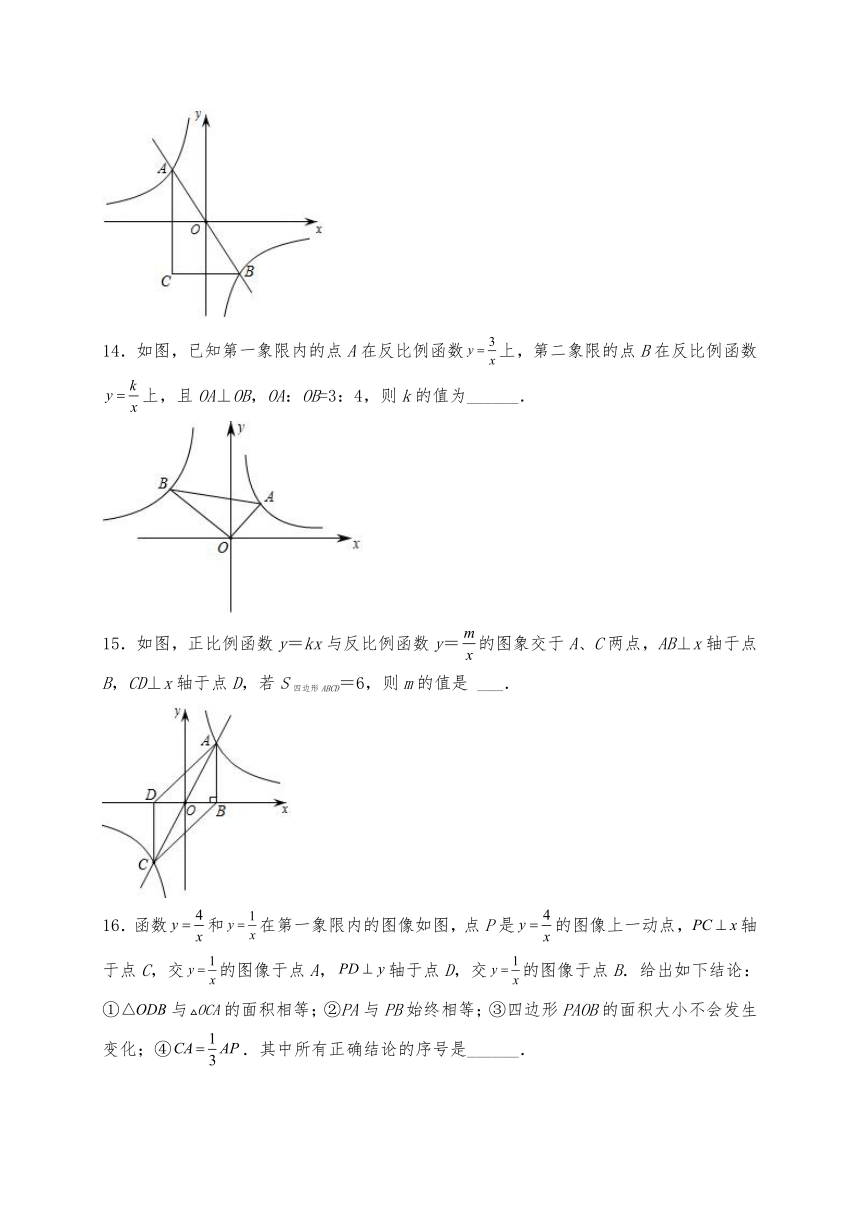
1.下面四个关系式中,y是x的反比例函数的是( )
A. B. C.y=5x+6 D.
2.如图,点P在反比例函数y=的图象上,PA⊥x轴于点A,PB⊥y轴于点B,且△APB的面积为2,则k等于( )
A.-4 B.-2 C.2 D.4
3.已知函数,当函数值为3时,自变量x的值为( )
A.﹣2 B.﹣ C.﹣2或﹣ D.﹣2或﹣
4.若M(-2,a),N(2,b),P(4,c)三点都在函数y=的图象上, 则a、b、c的大小关系为( )
A.a>b>c B.b>c>a C. c>a>b D.c>b>a
5.一个各面分别标有数字1、2、3、4、5、6的骰子,连续投掷二次,分别出现数字、,得到一个点,则既在直线上,又在双曲线上的概率为( )
A. B. C. D.
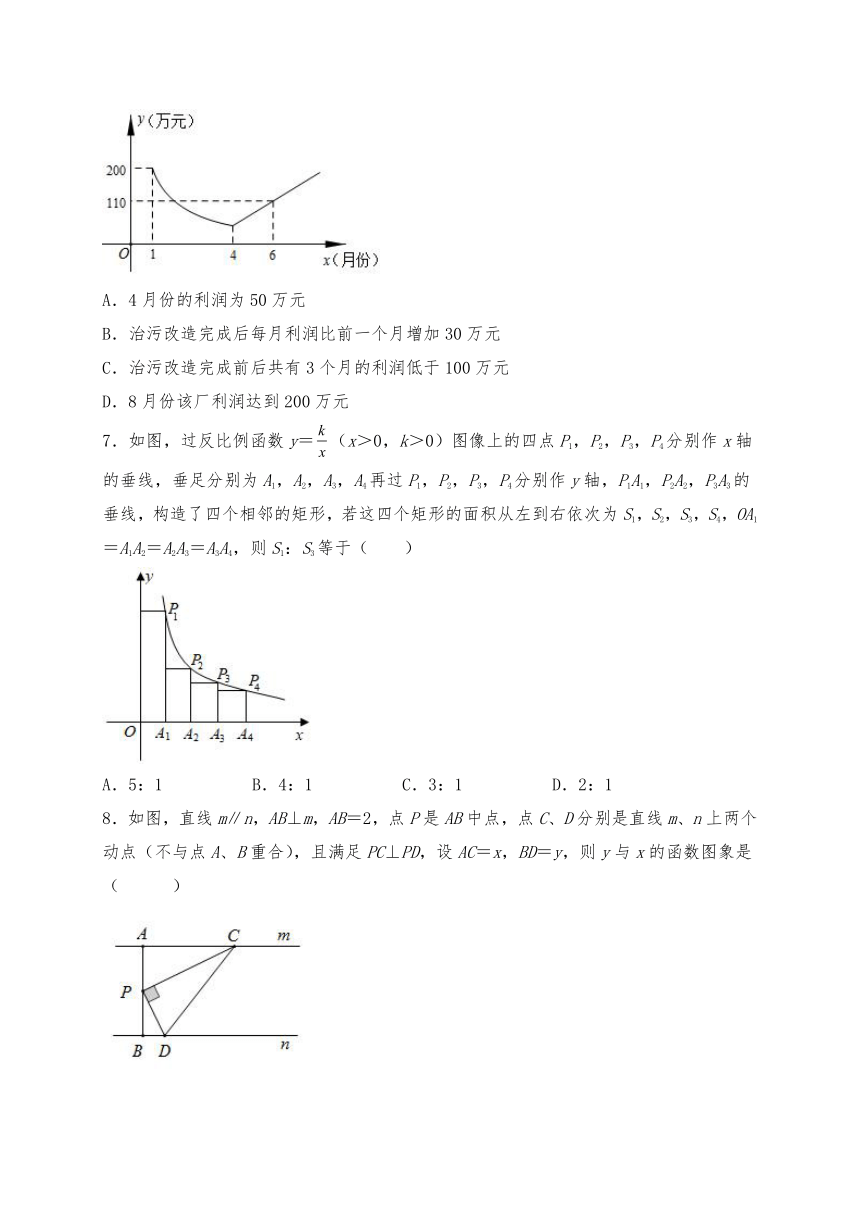
6.为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2019年1月开始限产进行治污改造,其月利润y(万元)与月份x之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的一部分,下列选项错误的是( )
A.4月份的利润为50万元
B.治污改造完成后每月利润比前一个月增加30万元
C.治污改造完成前后共有3个月的利润低于100万元
D.8月份该厂利润达到200万元
7.如图,过反比例函数y=(x>0,k>0)图像上的四点P1,P2,P3,P4分别作x轴的垂线,垂足分别为A1,A2,A3,A4再过P1,P2,P3,P4分别作y轴,P1A1,P2A2,P3A3的垂线,构造了四个相邻的矩形,若这四个矩形的面积从左到右依次为S1,S2,S3,S4,OA1=A1A2=A2A3=A3A4,则S1:S3等于( )
A.5:1 B.4:1 C.3:1 D.2:1
8.如图,直线m∥n,AB⊥m,AB=2,点P是AB中点,点C、D分别是直线m、n上两个动点(不与点A、B重合),且满足PC⊥PD,设AC=x,BD=y,则y与x的函数图象是( )
A. B. C. D.
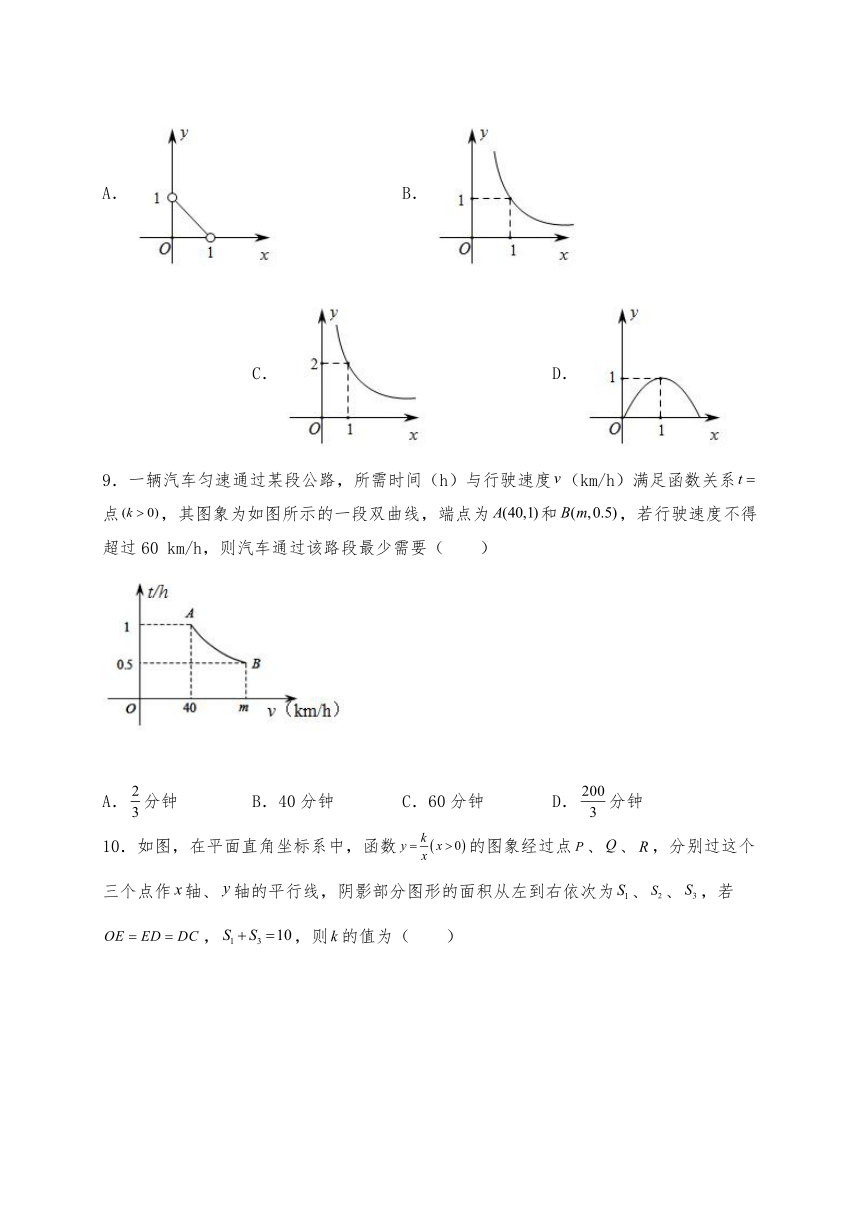
9.一辆汽车匀速通过某段公路,所需时间(h)与行驶速度(km/h)满足函数关系点,其图象为如图所示的一段双曲线,端点为和,若行驶速度不得超过60 km/h,则汽车通过该路段最少需要( )
A.分钟 B.40分钟 C.60分钟 D.分钟
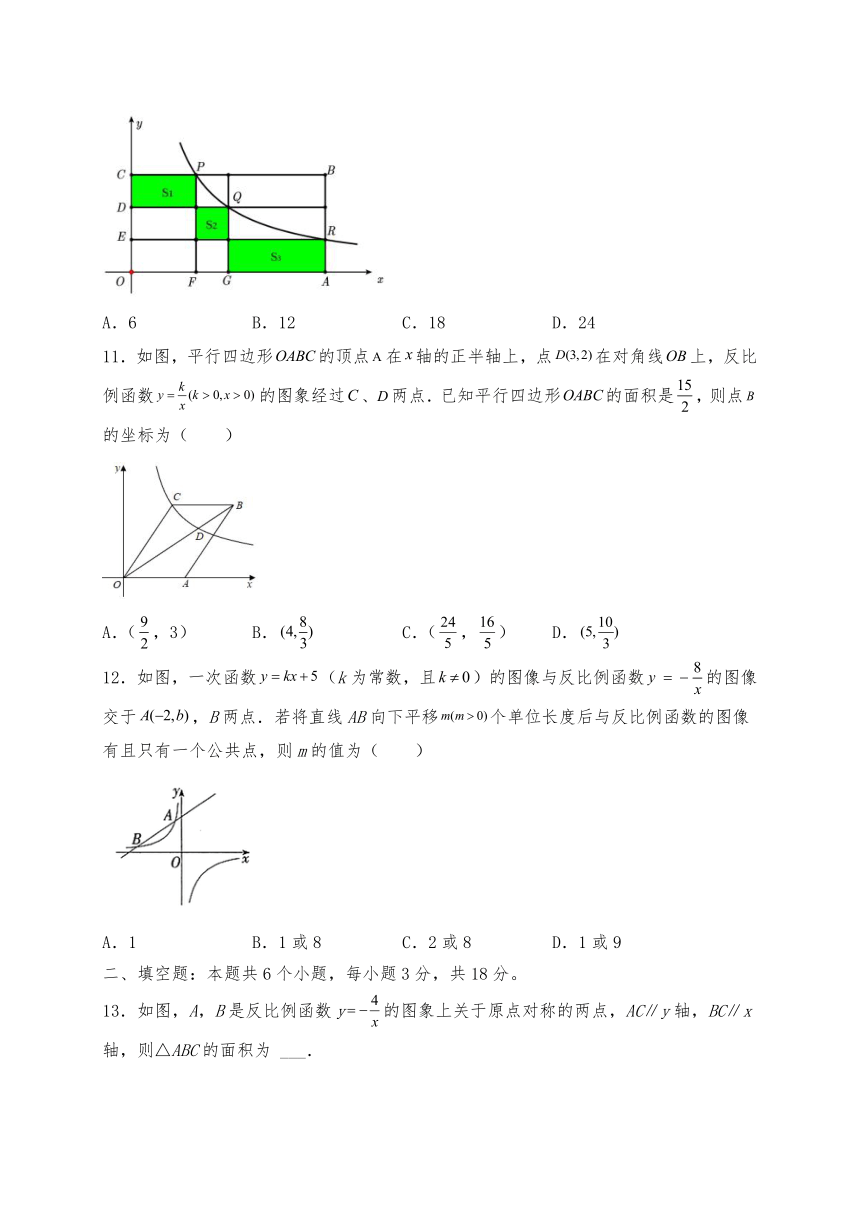
10.如图,在平面直角坐标系中,函数的图象经过点、、,分别过这个三个点作轴、轴的平行线,阴影部分图形的面积从左到右依次为、、,若,,则的值为( )
A.6 B.12 C.18 D.24
11.如图,平行四边形的顶点在轴的正半轴上,点在对角线上,反比例函数的图象经过、两点.已知平行四边形的面积是,则点的坐标为( )
A.(,3) B. C.(,) D.
12.如图,一次函数(k为常数,且)的图像与反比例函数的图像交于,B两点.若将直线AB向下平移个单位长度后与反比例函数的图像有且只有一个公共点,则m的值为( )
A.1 B.1或8 C.2或8 D.1或9
二、填空题:本题共6个小题,每小题3分,共18分。
13.如图,A,B是反比例函数y的图象上关于原点对称的两点,AC∥y轴,BC∥x轴,则△ABC的面积为 ___.
14.如图,已知第一象限内的点A在反比例函数上,第二象限的点B在反比例函数上,且OA⊥OB,OA:OB=3:4,则k的值为______.
15.如图,正比例函数y=kx与反比例函数y=的图象交于A、C两点,AB⊥x轴于点B,CD⊥x轴于点D,若S四边形ABCD=6,则m的值是 ___.
16.函数和在第一象限内的图像如图,点P是的图像上一动点,轴于点C,交的图像于点A,轴于点D,交的图像于点B.给出如下结论:①与的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④.其中所有正确结论的序号是______.
17.如图,在直角坐标系中,正方形的中心在原点O,且正方形的一组对边与x轴平行,点P(2a,a)是反比例函数的图象上与正方形的一个交点.若图中阴影部分的面积等于4,则这个反比例函数的解析式为_______.
18.如图是4个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作(为1~4的整数),函数()的图象为曲线.若曲线使得,这些点分布在它的两侧,每侧各2个点,则的取值范围是______.
三、解答题(19题6分,其余每题8分,共46分)
19.如图,点A(﹣2,y1)、B(﹣6,y2)在反比例函数y=(k<0)的图象上,AC⊥x轴,BD⊥y轴,垂足分别为C、D,AC与BD相交于点E.
(1)根据图象直接写出y1、y2的大小关系,并通过计算加以验证;
(2)结合以上信息,从①四边形OCED的面积为2,②BE=2AE这两个条件中任选一个作为补充条件,求k的值.你选择的条件是 (只填序号).
20.如图,设反比例函数的解析式为y=(k>0).
(1)若反比例函数与正比例函数y=2x的图象有一个交点的纵坐标为2,求k的值;
(2)若反比例函数的图象与过点M(﹣2,0)的直线l:y=kx+b的图象交于A、B两点,如图,当△ABO的面积为12时,求直线l的解析式.
21.已知一次函数的图象与反比例函数的图象在第一象限交于点,与轴交于点,与轴交于点,若,且.
(1)求反比例函数与一次函数的解析式;
(2)直接写出的解集;
(3)若点为轴上一点,求使的点的坐标.
22.某医药研究所研制了一种新药,在试验药效时发现:成人按规定剂量服用后,检测到从第5分钟起每分钟每毫升血液中含药量增加0.2微克,第100分钟达到最高,接着开始衰退.血液中含药量(微克)与时间(分钟)的函数关系如图.并发现衰退时与成反比例函数关系.
(1) ;
(2)当5≤x≤100时,与之间的函数关系式为 ;当时,与之间的函数关系式为 ;
(3)如果每毫升血液中含药量不低于10微克时是有效的,求出一次服药后的有效时间多久?
23.(2021·江苏泗阳·八年级期末)如图,已知反比例函数经过中、两点,直线交轴、轴于、两点.
(1)若、两点坐标分别为,,则__________,__________;
(2)若是中点且,求的面积.
(3)若,是否存在菱形,其中、两点横纵坐标均为正整数,如果存在,直接写出此时点坐标,如果不存在,简要说明一下理由.
24.在平面直角坐标系中,点绕点旋转得到点,我们称点是点的“影射点”
(1)若,则点的“影射点”的坐标是_________;点的“影射点”的坐标是_________;
(2)若点在一次函数的图像上,其“影射点”在一次函数的图像上,则的值是________;
(3)如图,已知点是点的“影射点",点是反比例函数图像上一点,若是以为直角边的等腰直角三角形,求的值.
答案
一、选择题。
D.A.A.B.C.D.C.B.B.B.AD.
二、填空题。
13.8
14.
15.3.
16.①③④
17..
18.
三、解答题
19.
(1)由于图象从左往右是上升的,即自变量增大,函数值也随之增大,故;
当x=-6时,;当x=-2时,
∵,k<0
∴
即
(2)选择条件①
∵AC⊥x轴,BD⊥y轴,OC⊥OD
∴四边形OCED是矩形
∴OD OC=2
∵OC=2
∴OD=1
即
∴点B的坐标为(-6,1)
把点B的坐标代入y=中,得k=-6
若选择条件②,即BE=2AE
∵AC⊥x轴,BD⊥y轴,OC⊥OD
∴四边形OCED是矩形
∴DE=OC,CE=OD
∵OC=2,DB=6
∴BE=DB-DE=DB-OC=4
∴
∵AE=AC-CE=AC-OD=
即
由(1)知:
∴k=-6
20.
解:(1)∵反比例函数与正比例函数y=2x的图象有一个交点的纵坐标为2,
把y=2代入y=2x求得x=1,
∴A(1,2),
把A(1,2)代入y=(k>0),得到3k=2,
∴k=;
(2)把M(﹣2,0)代入y=kx+b,可得b=2k,
∴y=kx+2k,
由消去y得到x2+2x﹣3=0,
解得x=﹣3或1,
∴B(﹣3,﹣k),A(1,3k),
∵△ABO的面积为12,
∴ 2 3k+ 2 k=12,
解得k=3,
∴直线l的解析式为y=3x+6.
21.
解:(1)如图,过点作轴于点
在和中
,
反比例函数解析式为
点坐标为,
点纵坐标为
将点纵坐标代入反比例函数解析式中,得点坐标为
将点坐标为,点坐标为代入一次函数得,
解得
一次函数解析式为
(2)或
(3)如图,过点作轴于点,连接、
设点坐标为,当时,
得
又点坐标为;点坐标为
解得:,
点坐标为或
22.
解:(1);
(2)当≤x≤100时,设与之间的函数关系式为
经过点,
解得:,
解析式为;
当时,与之间的函数关系式为,
经过点,
解得:,
函数的解析式为;
(3)令解得:,
令,解得:
分钟,
服药后能持续135分钟.
23.
解:(1)将A(2,3)代入反比例函数得,
即3=,
解得:k=6,
∴y=,
将B(6,b),代入y=得,
b==1,
故答案为:6,1.
(2)设B点坐标为(xB,),D点坐标为(0,b),A点坐标(xA,),
∵点A是BD的中点,
∴xA=,=,
得xA=,b=,
∴S△OAD=×xA×yD
=××
=6,
∵A为线段BD的中点,
∴S△OAD=S△OAB=6,
∴S平行四边形OACB=2×S△OAB=12.
(3)当k=12时,且A、B两点横纵坐标均为正整数,
∵12=1×12,12=2×6,12=3×4,
∴有以下可能:
①A(1,12),B(12,1),
此时C点坐标为,即(13,13),
②A(2,6),B(6,2),
此时C点坐标为,即(8,8),
③A(3,4),B(4,3),
此时C点坐标为,即(7,7).
24.
(1)设的坐标是的坐标是,
,绕点旋转180°,
,
,,
,
;,
故答案为:;,
(2)根据定义,是轴上的点,设,
点在一次函数,令,得,则与轴的交点为,
其“影射点”在一次函数,令,得,则与轴的交点为,
,
解得:,
故答案为:2,
(3)①如图,当时,连接 ,分别过向轴作垂线,垂足为,
,
,,
,
,
,
,
,
,
,
,
,
,
,
在上,
,
解得 或者,
,
,
,
,
②如图,当时,过点作轴,分别过向作垂线,垂足为,
,
,
,
,
,,
,
,
,,,
,
,
解得:,
,
,,
即,
,
在上,
,
解得 .
综上所述,或.
一、选择题:本题共12个小题,每小题3分,共36分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下面四个关系式中,y是x的反比例函数的是( )
A. B. C.y=5x+6 D.
2.如图,点P在反比例函数y=的图象上,PA⊥x轴于点A,PB⊥y轴于点B,且△APB的面积为2,则k等于( )
A.-4 B.-2 C.2 D.4
3.已知函数,当函数值为3时,自变量x的值为( )
A.﹣2 B.﹣ C.﹣2或﹣ D.﹣2或﹣
4.若M(-2,a),N(2,b),P(4,c)三点都在函数y=的图象上, 则a、b、c的大小关系为( )
A.a>b>c B.b>c>a C. c>a>b D.c>b>a
5.一个各面分别标有数字1、2、3、4、5、6的骰子,连续投掷二次,分别出现数字、,得到一个点,则既在直线上,又在双曲线上的概率为( )
A. B. C. D.
6.为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2019年1月开始限产进行治污改造,其月利润y(万元)与月份x之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的一部分,下列选项错误的是( )
A.4月份的利润为50万元
B.治污改造完成后每月利润比前一个月增加30万元
C.治污改造完成前后共有3个月的利润低于100万元
D.8月份该厂利润达到200万元
7.如图,过反比例函数y=(x>0,k>0)图像上的四点P1,P2,P3,P4分别作x轴的垂线,垂足分别为A1,A2,A3,A4再过P1,P2,P3,P4分别作y轴,P1A1,P2A2,P3A3的垂线,构造了四个相邻的矩形,若这四个矩形的面积从左到右依次为S1,S2,S3,S4,OA1=A1A2=A2A3=A3A4,则S1:S3等于( )
A.5:1 B.4:1 C.3:1 D.2:1
8.如图,直线m∥n,AB⊥m,AB=2,点P是AB中点,点C、D分别是直线m、n上两个动点(不与点A、B重合),且满足PC⊥PD,设AC=x,BD=y,则y与x的函数图象是( )
A. B. C. D.
9.一辆汽车匀速通过某段公路,所需时间(h)与行驶速度(km/h)满足函数关系点,其图象为如图所示的一段双曲线,端点为和,若行驶速度不得超过60 km/h,则汽车通过该路段最少需要( )
A.分钟 B.40分钟 C.60分钟 D.分钟
10.如图,在平面直角坐标系中,函数的图象经过点、、,分别过这个三个点作轴、轴的平行线,阴影部分图形的面积从左到右依次为、、,若,,则的值为( )
A.6 B.12 C.18 D.24
11.如图,平行四边形的顶点在轴的正半轴上,点在对角线上,反比例函数的图象经过、两点.已知平行四边形的面积是,则点的坐标为( )
A.(,3) B. C.(,) D.
12.如图,一次函数(k为常数,且)的图像与反比例函数的图像交于,B两点.若将直线AB向下平移个单位长度后与反比例函数的图像有且只有一个公共点,则m的值为( )
A.1 B.1或8 C.2或8 D.1或9
二、填空题:本题共6个小题,每小题3分,共18分。
13.如图,A,B是反比例函数y的图象上关于原点对称的两点,AC∥y轴,BC∥x轴,则△ABC的面积为 ___.
14.如图,已知第一象限内的点A在反比例函数上,第二象限的点B在反比例函数上,且OA⊥OB,OA:OB=3:4,则k的值为______.
15.如图,正比例函数y=kx与反比例函数y=的图象交于A、C两点,AB⊥x轴于点B,CD⊥x轴于点D,若S四边形ABCD=6,则m的值是 ___.
16.函数和在第一象限内的图像如图,点P是的图像上一动点,轴于点C,交的图像于点A,轴于点D,交的图像于点B.给出如下结论:①与的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④.其中所有正确结论的序号是______.
17.如图,在直角坐标系中,正方形的中心在原点O,且正方形的一组对边与x轴平行,点P(2a,a)是反比例函数的图象上与正方形的一个交点.若图中阴影部分的面积等于4,则这个反比例函数的解析式为_______.
18.如图是4个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作(为1~4的整数),函数()的图象为曲线.若曲线使得,这些点分布在它的两侧,每侧各2个点,则的取值范围是______.
三、解答题(19题6分,其余每题8分,共46分)
19.如图,点A(﹣2,y1)、B(﹣6,y2)在反比例函数y=(k<0)的图象上,AC⊥x轴,BD⊥y轴,垂足分别为C、D,AC与BD相交于点E.
(1)根据图象直接写出y1、y2的大小关系,并通过计算加以验证;
(2)结合以上信息,从①四边形OCED的面积为2,②BE=2AE这两个条件中任选一个作为补充条件,求k的值.你选择的条件是 (只填序号).
20.如图,设反比例函数的解析式为y=(k>0).
(1)若反比例函数与正比例函数y=2x的图象有一个交点的纵坐标为2,求k的值;
(2)若反比例函数的图象与过点M(﹣2,0)的直线l:y=kx+b的图象交于A、B两点,如图,当△ABO的面积为12时,求直线l的解析式.
21.已知一次函数的图象与反比例函数的图象在第一象限交于点,与轴交于点,与轴交于点,若,且.
(1)求反比例函数与一次函数的解析式;
(2)直接写出的解集;
(3)若点为轴上一点,求使的点的坐标.
22.某医药研究所研制了一种新药,在试验药效时发现:成人按规定剂量服用后,检测到从第5分钟起每分钟每毫升血液中含药量增加0.2微克,第100分钟达到最高,接着开始衰退.血液中含药量(微克)与时间(分钟)的函数关系如图.并发现衰退时与成反比例函数关系.
(1) ;
(2)当5≤x≤100时,与之间的函数关系式为 ;当时,与之间的函数关系式为 ;
(3)如果每毫升血液中含药量不低于10微克时是有效的,求出一次服药后的有效时间多久?
23.(2021·江苏泗阳·八年级期末)如图,已知反比例函数经过中、两点,直线交轴、轴于、两点.
(1)若、两点坐标分别为,,则__________,__________;
(2)若是中点且,求的面积.
(3)若,是否存在菱形,其中、两点横纵坐标均为正整数,如果存在,直接写出此时点坐标,如果不存在,简要说明一下理由.
24.在平面直角坐标系中,点绕点旋转得到点,我们称点是点的“影射点”
(1)若,则点的“影射点”的坐标是_________;点的“影射点”的坐标是_________;
(2)若点在一次函数的图像上,其“影射点”在一次函数的图像上,则的值是________;
(3)如图,已知点是点的“影射点",点是反比例函数图像上一点,若是以为直角边的等腰直角三角形,求的值.
答案
一、选择题。
D.A.A.B.C.D.C.B.B.B.AD.
二、填空题。
13.8
14.
15.3.
16.①③④
17..
18.
三、解答题
19.
(1)由于图象从左往右是上升的,即自变量增大,函数值也随之增大,故;
当x=-6时,;当x=-2时,
∵,k<0
∴
即
(2)选择条件①
∵AC⊥x轴,BD⊥y轴,OC⊥OD
∴四边形OCED是矩形
∴OD OC=2
∵OC=2
∴OD=1
即
∴点B的坐标为(-6,1)
把点B的坐标代入y=中,得k=-6
若选择条件②,即BE=2AE
∵AC⊥x轴,BD⊥y轴,OC⊥OD
∴四边形OCED是矩形
∴DE=OC,CE=OD
∵OC=2,DB=6
∴BE=DB-DE=DB-OC=4
∴
∵AE=AC-CE=AC-OD=
即
由(1)知:
∴k=-6
20.
解:(1)∵反比例函数与正比例函数y=2x的图象有一个交点的纵坐标为2,
把y=2代入y=2x求得x=1,
∴A(1,2),
把A(1,2)代入y=(k>0),得到3k=2,
∴k=;
(2)把M(﹣2,0)代入y=kx+b,可得b=2k,
∴y=kx+2k,
由消去y得到x2+2x﹣3=0,
解得x=﹣3或1,
∴B(﹣3,﹣k),A(1,3k),
∵△ABO的面积为12,
∴ 2 3k+ 2 k=12,
解得k=3,
∴直线l的解析式为y=3x+6.
21.
解:(1)如图,过点作轴于点
在和中
,
反比例函数解析式为
点坐标为,
点纵坐标为
将点纵坐标代入反比例函数解析式中,得点坐标为
将点坐标为,点坐标为代入一次函数得,
解得
一次函数解析式为
(2)或
(3)如图,过点作轴于点,连接、
设点坐标为,当时,
得
又点坐标为;点坐标为
解得:,
点坐标为或
22.
解:(1);
(2)当≤x≤100时,设与之间的函数关系式为
经过点,
解得:,
解析式为;
当时,与之间的函数关系式为,
经过点,
解得:,
函数的解析式为;
(3)令解得:,
令,解得:
分钟,
服药后能持续135分钟.
23.
解:(1)将A(2,3)代入反比例函数得,
即3=,
解得:k=6,
∴y=,
将B(6,b),代入y=得,
b==1,
故答案为:6,1.
(2)设B点坐标为(xB,),D点坐标为(0,b),A点坐标(xA,),
∵点A是BD的中点,
∴xA=,=,
得xA=,b=,
∴S△OAD=×xA×yD
=××
=6,
∵A为线段BD的中点,
∴S△OAD=S△OAB=6,
∴S平行四边形OACB=2×S△OAB=12.
(3)当k=12时,且A、B两点横纵坐标均为正整数,
∵12=1×12,12=2×6,12=3×4,
∴有以下可能:
①A(1,12),B(12,1),
此时C点坐标为,即(13,13),
②A(2,6),B(6,2),
此时C点坐标为,即(8,8),
③A(3,4),B(4,3),
此时C点坐标为,即(7,7).
24.
(1)设的坐标是的坐标是,
,绕点旋转180°,
,
,,
,
;,
故答案为:;,
(2)根据定义,是轴上的点,设,
点在一次函数,令,得,则与轴的交点为,
其“影射点”在一次函数,令,得,则与轴的交点为,
,
解得:,
故答案为:2,
(3)①如图,当时,连接 ,分别过向轴作垂线,垂足为,
,
,,
,
,
,
,
,
,
,
,
,
,
,
在上,
,
解得 或者,
,
,
,
,
②如图,当时,过点作轴,分别过向作垂线,垂足为,
,
,
,
,
,,
,
,
,,,
,
,
解得:,
,
,,
即,
,
在上,
,
解得 .
综上所述,或.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
