北师大版九年级数学上册试题第四章 图形的相似 复习卷(含答案)
文档属性
| 名称 | 北师大版九年级数学上册试题第四章 图形的相似 复习卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 312.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-20 08:29:25 | ||
图片预览


文档简介
第四章 《图形的相似》复习卷
一、选择题。
1.若(,,,均不为0),则( )
A. B. C. D.
2.如图,在平面直角坐标系中,以原点O为位似中心,将△ABO扩大到原来的2倍,得,到△A'B'O.若点B的坐标为(2,1),则点B'的坐标为( )
A.(2,4) B.(4.2)
C.(2,4)或(﹣2,﹣4) D.(4,2)或(﹣4,﹣2)
3.如图,两条直线被三条平行线所截,若DE=3,EF=6,BC=8,则AC=( )
A.4 B.8 C.12 D.9
4.下列说法不正确的是( )
A.将一个矩形风景画的四周镶上宽度相等的金边后得到的新矩形与原矩形相似
B.若线段a=5cm,b=2cm,则a:b=5:2
C.若线段AB=cm,C是线段AB的黄金分割点,且AC>BC,则AC=cm
D.若两个相似多边形的面积比为16:9,那么这两个相似多边形的周长比是4:3
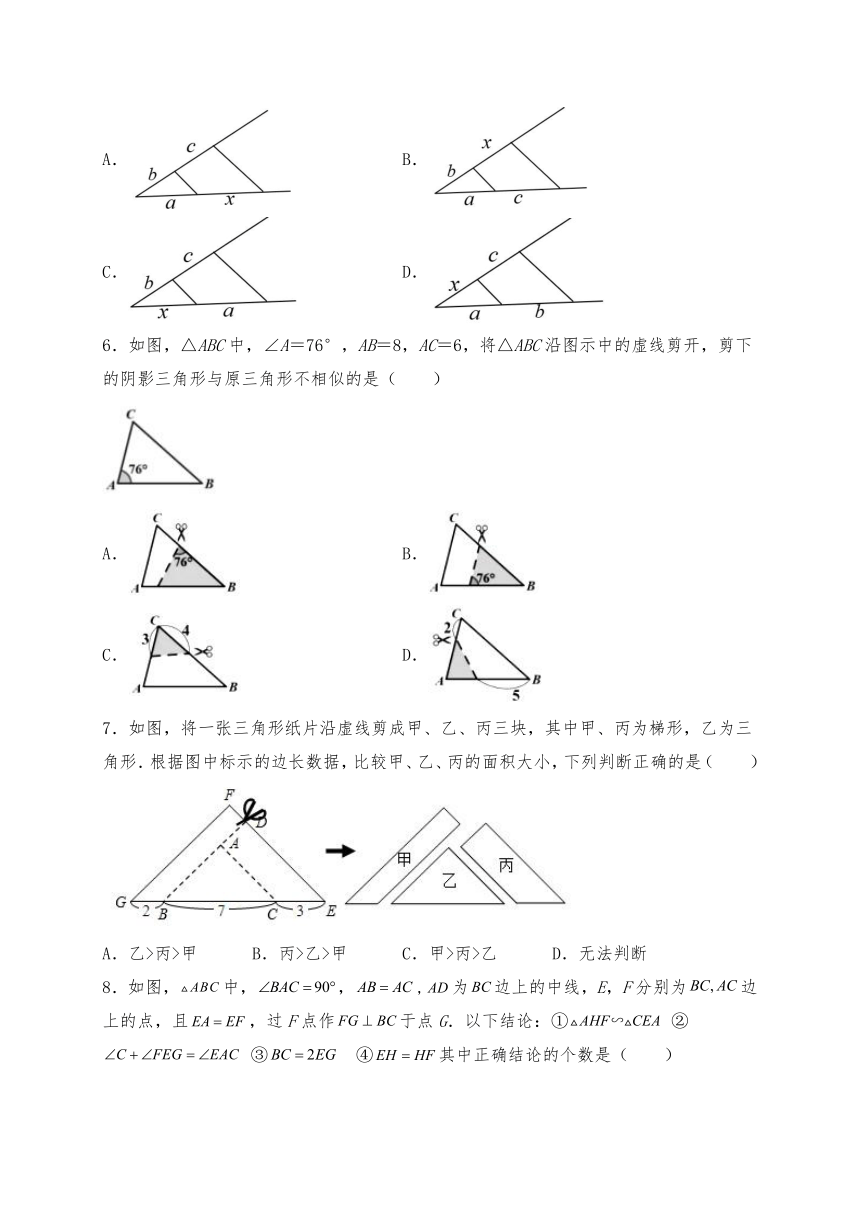
5.已知线段a、b、c,作线段x,使b:a=x:c,则正确的作法是( )
A. B.
C. D.
6.如图,△ABC中,∠A=76°,AB=8,AC=6,将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
A. B.
C. D.
7.如图,将一张三角形纸片沿虚线剪成甲、乙、丙三块,其中甲、丙为梯形,乙为三角形.根据图中标示的边长数据,比较甲、乙、丙的面积大小,下列判断正确的是( )
A.乙>丙>甲 B.丙>乙>甲 C.甲>丙>乙 D.无法判断
8.如图,中,,,为边上的中线,E,F分别为边上的点,且,过F点作于点G.以下结论:① ② ③ ④其中正确结论的个数是( )
A.1 B.2 C.3 D.4
二、填空题。
9.如图,主持人主持节目时,站在舞台的黄金分割点处最自然得体.如果舞台AB的长为10米,一名主持人现在站在A处,若她想最自然得体,则她至少走________________.
10.如图:中,是AB边上一点(与AB不重合),过点作直线截,所截得的三角形与原相似,满足这样条件的直线共有____条.
11.如图所示,一般书本的纸张是原纸张多次对开得到,矩形沿对开后,再把矩形沿对开,依次类推,若各种开本的矩形都相似,那么的值为________.
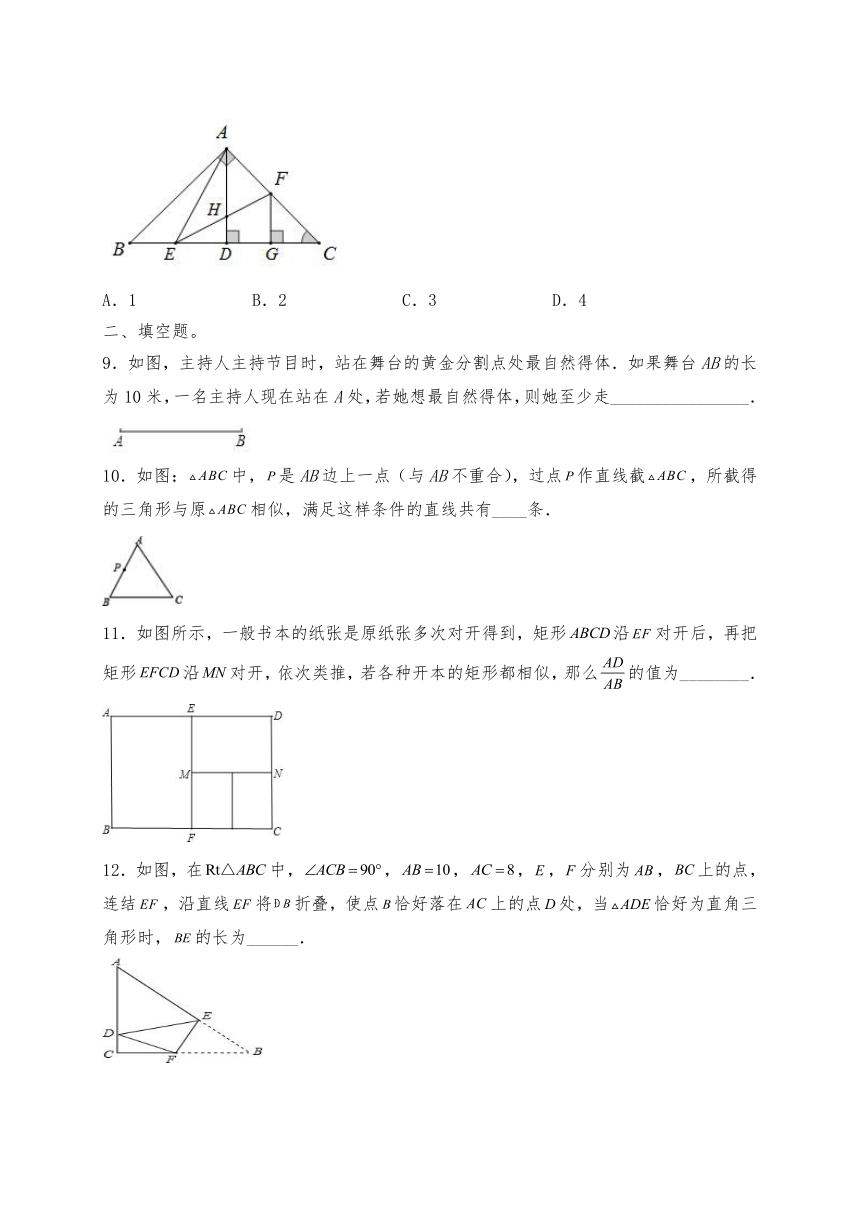
12.如图,在中,,,,,分别为,上的点,连结,沿直线将折叠,使点恰好落在上的点处,当恰好为直角三角形时,的长为______.
三、解答题。
13.如图,已知直线l1、l2、l3分别截直线l4于点A、B、C,截直线l5于点D、E、F,且
(1)如果AB=3,BC=6,DE=4,求EF的长;
(2)如果DE:EF=2:3,AC=25,求AB的长.
14.已知:如图,有一块锐角三角形余料ABC,它的边BC=12cm,高AH=8cm,要把它加工成矩形零件,使矩形零件的一边DE在BC边上,其余两个顶点G、F分别在边AB和AC上.
(1)当加工的矩形零件的两边EF:GF=2:3时,求这个矩形零件的面积;
(2)当矩形零件DEFG与△ABC的面积之比为4:9时,求此时矩形零件DEFG的两边EF:GF的值.
15.已知四边形ABCD中,E,F分别是AB,AD边上的点,DE与CF交于点G.
(1)问题提出:如图1,如果四边形ABCD是正方形,当E、F分别是AB、AD的中点时,则DE与CF的数量关系为 ,位置关系为 .
(2)问题探究:如图2,若四边形ABCD是矩形,且DE⊥CF.求证:.
(3)应用拓展:某农庄有如图2的一块矩形菜园,BC边长40米,AB边长24米.两条互相垂直的过道DE、CF将菜园分成四块种植区,其中过道一端F距菜园顶点D3.6米.已知AD边紧挨着一条河流,现需从AD边上某处M挖两条直直的引水渠,将河水分别引至E、C两处浇灌蔬菜,问两条水渠长度之和ME+MC的最小值是多少?
答案
一、选择题。
C.D.C.A.B.C.B.D.
二、填空题。
9.米.
10.4.
11..
12.或.
三、解答题。
13.
解(1),
AB=3,BC=6,DE=4,
经检验:符合题意;
(2),
而DE:EF=2:3,
14.
解:(1)∵矩形零件的两边EF:GF=2:3,
∴设EF=2x,GF=3x,
∵FG∥BC,
∴△AGF∽△ABC,
∴,
则,
解得:x=2,
则EF=4cm,FG=6cm,
故这个矩形零件的面积为:24cm2;
(2)∵BC=12cm,高AH=8cm,
∴S△ABC=×12×8=48(cm2),
∵矩形零件DEFG与△ABC的面积之比为4:9,
∴矩形零件DEFG的面积为:(cm2),
设EF=acm,则cm,
∵由(1)得:,
∴,
解得:,,
当,则FG=8,此时;
当,则FG=4,此时.
15.
解:(1)∵四边形ABCD是正方形,
∴AB=AD=CD=BC,
∴∠A=∠CDF=90°,
∵E、F分别是AB、AD的中点,
∴AE=DF,
在△ADE和△DCF中,
∴△ADE≌△DCF(SAS),
∴DE=CF,∠ADE=∠DCF,
∴∠ADE+∠CDG=∠ADC=90 ,
∴∠DCF+∠CDG=90°,
∴∠CGD=90 ,
∴DE⊥CF,
(2)∵四边形ABCD是矩形,
∴∠A=∠CDF=90°,
∴∠ADE+∠AED=90° ,
∴DE⊥CF,
∴∠DGF=90°,
∴∠ADE+∠DFG=90°,
∴∠AED=∠DFC,
∴△ADE∽△DCF,
∴
(3)矩形ABCD中,AD=BC=40米,DC=AB=24米,DF=3.6米,
由(2)知:△ADE∽△DCF,
∴,
∴(米),
延长BA到点E ,使AE =AE=6米,则AD垂直平分EE ,
∴EM=E M,
由“两点之间,线段最短”可知:当点M在CE 与AD的交点处时,E M+CM的值最小,从而EM+CM的值最小,最小值为CE 的长,
在Rt△BCE 中,
BE =AB+AE =24+6=30(米),由勾股定理,得
(米),
即两条水渠长度之和EM+CM的最小值是50米.
一、选择题。
1.若(,,,均不为0),则( )
A. B. C. D.
2.如图,在平面直角坐标系中,以原点O为位似中心,将△ABO扩大到原来的2倍,得,到△A'B'O.若点B的坐标为(2,1),则点B'的坐标为( )
A.(2,4) B.(4.2)
C.(2,4)或(﹣2,﹣4) D.(4,2)或(﹣4,﹣2)
3.如图,两条直线被三条平行线所截,若DE=3,EF=6,BC=8,则AC=( )
A.4 B.8 C.12 D.9
4.下列说法不正确的是( )
A.将一个矩形风景画的四周镶上宽度相等的金边后得到的新矩形与原矩形相似
B.若线段a=5cm,b=2cm,则a:b=5:2
C.若线段AB=cm,C是线段AB的黄金分割点,且AC>BC,则AC=cm
D.若两个相似多边形的面积比为16:9,那么这两个相似多边形的周长比是4:3
5.已知线段a、b、c,作线段x,使b:a=x:c,则正确的作法是( )
A. B.
C. D.
6.如图,△ABC中,∠A=76°,AB=8,AC=6,将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
A. B.
C. D.
7.如图,将一张三角形纸片沿虚线剪成甲、乙、丙三块,其中甲、丙为梯形,乙为三角形.根据图中标示的边长数据,比较甲、乙、丙的面积大小,下列判断正确的是( )
A.乙>丙>甲 B.丙>乙>甲 C.甲>丙>乙 D.无法判断
8.如图,中,,,为边上的中线,E,F分别为边上的点,且,过F点作于点G.以下结论:① ② ③ ④其中正确结论的个数是( )
A.1 B.2 C.3 D.4
二、填空题。
9.如图,主持人主持节目时,站在舞台的黄金分割点处最自然得体.如果舞台AB的长为10米,一名主持人现在站在A处,若她想最自然得体,则她至少走________________.
10.如图:中,是AB边上一点(与AB不重合),过点作直线截,所截得的三角形与原相似,满足这样条件的直线共有____条.
11.如图所示,一般书本的纸张是原纸张多次对开得到,矩形沿对开后,再把矩形沿对开,依次类推,若各种开本的矩形都相似,那么的值为________.
12.如图,在中,,,,,分别为,上的点,连结,沿直线将折叠,使点恰好落在上的点处,当恰好为直角三角形时,的长为______.
三、解答题。
13.如图,已知直线l1、l2、l3分别截直线l4于点A、B、C,截直线l5于点D、E、F,且
(1)如果AB=3,BC=6,DE=4,求EF的长;
(2)如果DE:EF=2:3,AC=25,求AB的长.
14.已知:如图,有一块锐角三角形余料ABC,它的边BC=12cm,高AH=8cm,要把它加工成矩形零件,使矩形零件的一边DE在BC边上,其余两个顶点G、F分别在边AB和AC上.
(1)当加工的矩形零件的两边EF:GF=2:3时,求这个矩形零件的面积;
(2)当矩形零件DEFG与△ABC的面积之比为4:9时,求此时矩形零件DEFG的两边EF:GF的值.
15.已知四边形ABCD中,E,F分别是AB,AD边上的点,DE与CF交于点G.
(1)问题提出:如图1,如果四边形ABCD是正方形,当E、F分别是AB、AD的中点时,则DE与CF的数量关系为 ,位置关系为 .
(2)问题探究:如图2,若四边形ABCD是矩形,且DE⊥CF.求证:.
(3)应用拓展:某农庄有如图2的一块矩形菜园,BC边长40米,AB边长24米.两条互相垂直的过道DE、CF将菜园分成四块种植区,其中过道一端F距菜园顶点D3.6米.已知AD边紧挨着一条河流,现需从AD边上某处M挖两条直直的引水渠,将河水分别引至E、C两处浇灌蔬菜,问两条水渠长度之和ME+MC的最小值是多少?
答案
一、选择题。
C.D.C.A.B.C.B.D.
二、填空题。
9.米.
10.4.
11..
12.或.
三、解答题。
13.
解(1),
AB=3,BC=6,DE=4,
经检验:符合题意;
(2),
而DE:EF=2:3,
14.
解:(1)∵矩形零件的两边EF:GF=2:3,
∴设EF=2x,GF=3x,
∵FG∥BC,
∴△AGF∽△ABC,
∴,
则,
解得:x=2,
则EF=4cm,FG=6cm,
故这个矩形零件的面积为:24cm2;
(2)∵BC=12cm,高AH=8cm,
∴S△ABC=×12×8=48(cm2),
∵矩形零件DEFG与△ABC的面积之比为4:9,
∴矩形零件DEFG的面积为:(cm2),
设EF=acm,则cm,
∵由(1)得:,
∴,
解得:,,
当,则FG=8,此时;
当,则FG=4,此时.
15.
解:(1)∵四边形ABCD是正方形,
∴AB=AD=CD=BC,
∴∠A=∠CDF=90°,
∵E、F分别是AB、AD的中点,
∴AE=DF,
在△ADE和△DCF中,
∴△ADE≌△DCF(SAS),
∴DE=CF,∠ADE=∠DCF,
∴∠ADE+∠CDG=∠ADC=90 ,
∴∠DCF+∠CDG=90°,
∴∠CGD=90 ,
∴DE⊥CF,
(2)∵四边形ABCD是矩形,
∴∠A=∠CDF=90°,
∴∠ADE+∠AED=90° ,
∴DE⊥CF,
∴∠DGF=90°,
∴∠ADE+∠DFG=90°,
∴∠AED=∠DFC,
∴△ADE∽△DCF,
∴
(3)矩形ABCD中,AD=BC=40米,DC=AB=24米,DF=3.6米,
由(2)知:△ADE∽△DCF,
∴,
∴(米),
延长BA到点E ,使AE =AE=6米,则AD垂直平分EE ,
∴EM=E M,
由“两点之间,线段最短”可知:当点M在CE 与AD的交点处时,E M+CM的值最小,从而EM+CM的值最小,最小值为CE 的长,
在Rt△BCE 中,
BE =AB+AE =24+6=30(米),由勾股定理,得
(米),
即两条水渠长度之和EM+CM的最小值是50米.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
