北师大版九年级数学上册试题第五章 投影与视图 单元测试卷(含答案)
文档属性
| 名称 | 北师大版九年级数学上册试题第五章 投影与视图 单元测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 546.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-20 08:30:14 | ||
图片预览

文档简介
第五章 《投影与视图》单元测试卷
一、选择题:本题共12个小题,每小题3分,共36分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.如图所示的六角螺栓,其俯视图是( )
A. B.
C. D.
2.当你在笔直的公路上乘车由A至E的过程中(如图所示),发现路边有两栋建筑物,那么不能看到较高建筑物PD的路段是( )
A.AB B.BC C.CD D.DE
3.下列四个几何体中,左视图形状与其它三个不同的是( )
A. B. C. D.
4.如图是小红在某天四个时刻看到一根木棒及其影子的情况,那么她看到的先后顺序是( )
A.①②③④ B.④③①② C.④①③② D.②①③④
5.图(1)表示一个正五棱柱形状的高大建筑物,图(2)是它的俯视图.小健站在地面观察该建筑物,当他在图(2)中的阴影部分所表示的区域活动时,能同时看到建筑物的三个侧面,图中∠MPN的度数为( )
A.30° B.36° C.45° D.72°
6.如图是由10个大小完全相同的小正方体搭成的几何体的俯视图,小正方体上的数字为对应位置上小正方体的数量,将数字“3”上的小正方体向数字“2”上的位置平移一个,下面说法正确的是( )
A.主视图与俯视图不变 B.左视图与俯视图不变
C.主视图与左视图改变 D.三种视图都不变
7.小明同学拿着一个如图所示的三角形木架在太阳光下玩,他不断变换三角形木架的位置,他说他发现了三角形木架在地上出现过的影子有四种:①点;②线段;③三角形;④四边形.你认为小明说法中正确的个数有( )
A.4个 B.3个 C.2个 D.1个
8.长方体的主视图和左视图如图所示(单位:cm),则其俯视图的面积是( )
A.10cm2 B.12cm2 C.15cm2 D.20cm2
9.我们知道,面动成体!如图,正方形ABCD边长为3cm,以直线AB为轴将正方形旋转一周所得几何体,从正面看到的形状图的面积是( ).
A.9 cm2 B.18 cm2
C.9π cm2 D.27π cm2
10.由若干个相同的小立方体搭成的一个几何体的主视图和俯视图如图所示,俯视图的方格中的字母和数字表示该位置上小立方体的个数,则以下说法正确的是( )
A.x=1或2,y=3 B.x=1或2,y=1或3
C.x=1,y=1或3 D.x=2,y=1或3
11.圆桌面(桌面中间有一个直径为1m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为2m,桌面离地面1m,若灯泡离地面2m,则地面圆环形阴影的面积是( )
A.2πm2 B.3πm2 C.6πm2 D.12πm2
12.如图是一个圆锥的三视图,俯视图是直径为的圆,主视图和左视图都是底为,腰为的等腰三角形,这个圆锥的体积是=( )
A. B. C. D.
二、填空题:本题共6个小题,每小题3分,共18分。
13.广场上一个大型艺术字板块在地上的投影如图所示,则该投影属于_____.(填写“平行投影”或“中心投影”)
14.如图,一棵树(AB)的高度为7.5米,下午某一个时刻它在水平地面上形成的树影长(BE)为10米,现在小明想要站这棵树下乘凉,他的身高为1.5米,那么他最多可以离开树干多少米才可以不被阳光晒到?____.
15.如图,上、下底面为全等的正六边形礼盒,其主视图与左视图均由矩形构成,主视图中大矩形边长如图,左视图中包含两个全等的矩形,如果用彩色胶带按如图包扎礼盒,所需胶带长度至少为___________ cm.(精确到0.001 cm)
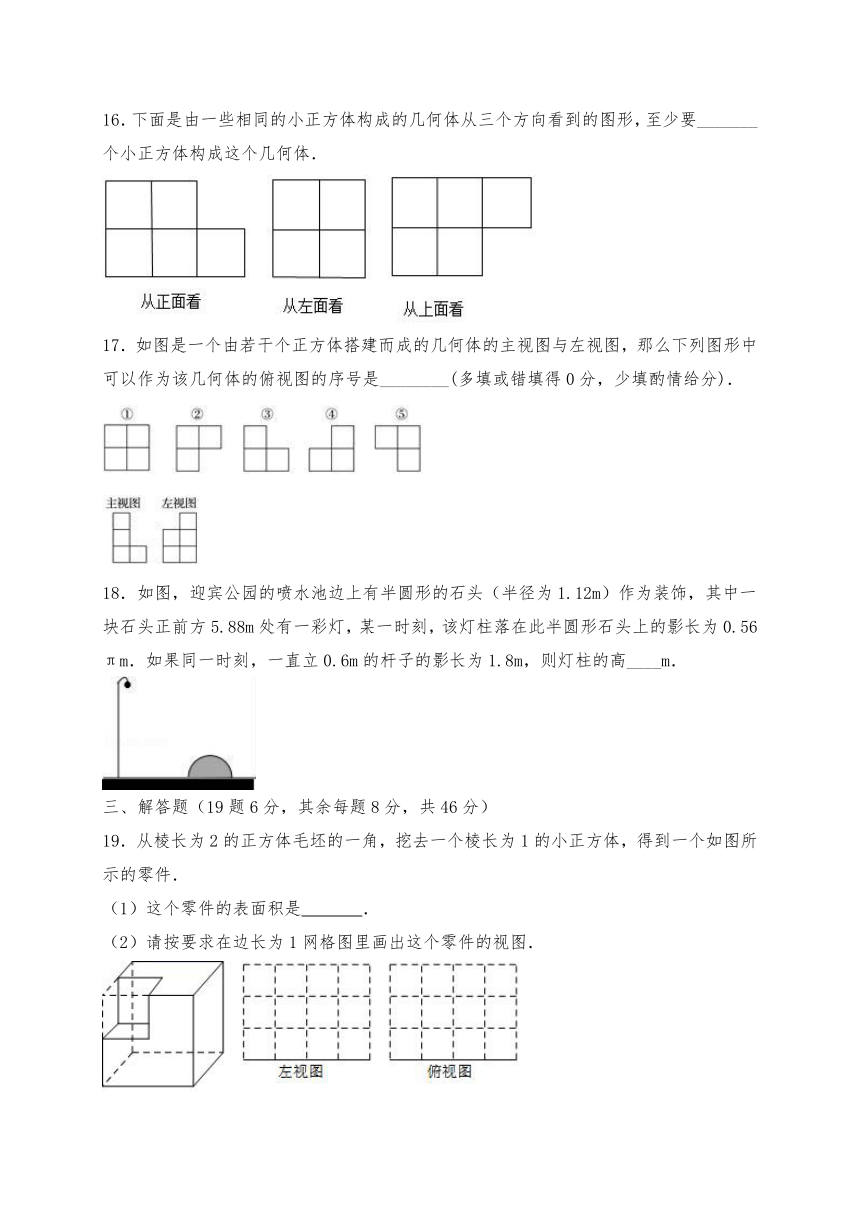
16.下面是由一些相同的小正方体构成的几何体从三个方向看到的图形,至少要_______个小正方体构成这个几何体.
17.如图是一个由若干个正方体搭建而成的几何体的主视图与左视图,那么下列图形中可以作为该几何体的俯视图的序号是________(多填或错填得0分,少填酌情给分).
18.如图,迎宾公园的喷水池边上有半圆形的石头(半径为1.12m)作为装饰,其中一块石头正前方5.88m处有一彩灯,某一时刻,该灯柱落在此半圆形石头上的影长为0.56πm.如果同一时刻,一直立0.6m的杆子的影长为1.8m,则灯柱的高____m.
三、解答题(19题6分,其余每题8分,共46分)
19.从棱长为2的正方体毛坯的一角,挖去一个棱长为1的小正方体,得到一个如图所示的零件.
(1)这个零件的表面积是 .
(2)请按要求在边长为1网格图里画出这个零件的视图.
20.如图1,国庆期间某广场旗杆附近搭建了一座花篮.图2为从该场景抽象出的数学模型,已知花篮高度,某一时刻花篮在阳光下的投影.
(1)请你用尺规作图法在图2中作出此时旗杆在阳光下的投影;(不写作法,保留作图痕迹)
(2)在测量的投影时,同时测出旗杆在阳光下的投影,请你计算的长.
21.如图,是某公园的一个圆形桌面的主视图,是该桌面在一路灯下的影子,是一个圆形凳面的主视图.(桌面、凳面均与地面平行)
(1)请标出路灯的位置,并画出在该路灯下的影子;(保留画图痕迹,光线用虚线表示)
(2)若桌面直径和桌面与地面的距离均为,并测得影子,求路灯与地面的距离.
22.一透明的敞口正方体容器装有一些液体,棱AB始终在水平桌面上,容器底部的倾斜角为α,(∠CBE=α,如图1所示),此时液面刚好过棱CD,并与棱BB'交于点Q,此时液体的形状为直三棱柱,三视图及尺寸如图2所示,求当正方体平放(正方形ABCD在桌面上)时,液体的深度.
23.如图,如图几何体是由若干棱长为1的小立方体按一定规律在地面上摆成的,若将露出的表面都涂上颜色(底面不涂色),观察该图,探究其中的规律.
(1)第1个几何体中只有2个面涂色的小立方体共有 个;第2个几何体中只有2个面涂色的小立方体共有 个;第3个几何体中只有2个面涂色的小立方体共有 个.
(2)求出第10个几何体中只有2个面涂色的小立方体的块数.
(3)求出前100个几何体中只有2个面涂色的小立方体的块数的和.
24.图1至图7中的网格图均是20×20的等距网格图(每个小方格的边长均为1个单位长).侦察兵王凯在P点观察区域MNCD内的活动情况.当5个单位长的列车(图中的)以每秒1个单位长的速度在铁路线MN上通过时,列车将阻挡王凯的部分视线,在区域MNCD内形成盲区(不考虑列车的宽度和车厢间的缝隙).设列车车头运行到M点的时刻为0,列车从M点向N点方向运行的时间为t(秒).
(1)在区域MNCD内,请你针对图1,图2,图3,图4中列车位于不同位置的情形分别画出相应的盲区,并在盲区内涂上阴影.
(2)只考虑在区域ABCD内开成的盲区.设在这个区域内的盲区面积是y(平方单位).
①如图5,当5≤t≤10时,请你求出用t表示y的函数关系式;
②如图6,当10≤t≤15时,请你求出用t表示y的函数关系式;
③如图7,当15≤t≤20时,请你求出用t表示y的函数关系式;
④根据①~③中得到的结论,请你简单概括y随t的变化而变化的情况.
(3)根据上述研究过程,请你按不同的时段,就列车行驶过程中在区域MNCD内所形成盲区的面积大小的变化情况提出一个综合的猜想.
答案
一、选择题。
A.B.B.B.B.B.C.B.B.A.B.A
二、填空题。
13.中心投影
14.8.
15.431.769.
16.7
17.①②③
18.(m).
三、解答题
19.
解:(1)2×2×6=24.
这个零件的表面积是24,
故答案为:24.
(2)如图所示:
20.
解:(1)如图就是的投影.
(2)由作图可知,
,
,
∴△ABC∽△DEF,
,即,
.
答:的长为.
21.
解:(1)如图,路灯和线段即为所画.
(2)如图,过点作,交于点,
∵,
∴,,.
∴∽,
∴.
∵,,,
∴,
∴.
答:路灯与地面的距离为.
22.
解:∵CQ=5dm,AB=4dm,
是正方体
∴BQ===3(dm),
∴液体的体积为:V液=×3×4×4=24(dm3),
正方形的面积为
∴液体的深度是24÷16=1.5(dm).
23.
解:(1)观察图形可知:图①中,两面涂色的小立方体共有4个;
图②中,两面涂色的小立方体共有12个;
图③中,两面涂色的小立方体共有20个;
故答案为:4,12,20;
(2)观察图形可知:图①中,只有2个面涂色的小立方体共有4个;
图②中,只有2个面涂色的小立方体共有12个;
图③中,只有2个面涂色的小立方体共有20个.
4,12,20都是4的倍数,可分别写成4×1,4×3,4×5的形式,
因此,第n个图中两面涂色的小立方体共有4(2n-1)=8n-4,
则第100个几何体中只有2个面涂色的小立方体共有8×100-4=796个;
(3)(8×1-4)+(8×2-4)+(8×3-4)+(8×4-4)+(8×5-4)+…+(8×100-4)
=8×(1+2+3+4+…+100)-100×4
=40000(个).
故前100个几何体中只有2个面涂色的小立方体的个数的和为40000个.
24.
(1)在P视点看不见的列车后的区域就是盲区,也就是过P和列车的两端的射线交CD于两点,这两点和列车两端构成的梯形就是所指的盲区.如图1的梯形AA1D1D,图2的梯形A2B2C2D2,图3的梯形B3BCC3.
(2)①如图1,当5≤t≤10时,盲区是梯形AA1D1D
∵O是PQ中点,且OA∥QD,
∴A1,A分别是PD1和PD中点
∴A1A是△PD1D的中位线.
又∵A1A=t-5,∴D1D=2(t-5)
而梯形AA1D1D的高OQ=10,
∴y= [(t-5)+2(t-5)]×10=15t-75
∴y=15t-75.
②如图2,当10≤t≤15时,盲区是梯形A2B2C2D2,
易知A2B2是△PC2D2的中位线,且A2B2=5,
∴C2D2=10
又∵梯形A2B2C2D2的高OQ=10,
∴y=(5+10)×10=75
∴y=75.
③如图3,当15≤t≤20时,盲区是梯形B3BCC3
易知BB3是△PCC3的中位线
且BB3=5-(t-15)=20-t
又∵梯形B3BCC3的高OQ=10,
∴y= [(20-t)+2(20-t)]×10=300-15t
∴y=300-15t.
④当5≤t≤10时,由一次函数y=15t-75的性质可知,盲区的面积由0逐渐增大到75;
当10≤t≤15时,盲区的面积y为定值75;
当15≤t≤20时,由一次函数y=300-15t的性质可知,盲区的面积由75逐渐减小到0.
(3)通过上述研究可知,列车从M点向N点方向运行的过程中,在区域MNCD内盲区面积大小的变化是:
①在0≤t≤10时段内,盲区面积从0逐渐增大到75;
②在10≤t≤15时段内,盲区的面积为定值75;
③在15≤t≤20时段内,盲区面积从75逐渐减小到0.
一、选择题:本题共12个小题,每小题3分,共36分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.如图所示的六角螺栓,其俯视图是( )
A. B.
C. D.
2.当你在笔直的公路上乘车由A至E的过程中(如图所示),发现路边有两栋建筑物,那么不能看到较高建筑物PD的路段是( )
A.AB B.BC C.CD D.DE
3.下列四个几何体中,左视图形状与其它三个不同的是( )
A. B. C. D.
4.如图是小红在某天四个时刻看到一根木棒及其影子的情况,那么她看到的先后顺序是( )
A.①②③④ B.④③①② C.④①③② D.②①③④
5.图(1)表示一个正五棱柱形状的高大建筑物,图(2)是它的俯视图.小健站在地面观察该建筑物,当他在图(2)中的阴影部分所表示的区域活动时,能同时看到建筑物的三个侧面,图中∠MPN的度数为( )
A.30° B.36° C.45° D.72°
6.如图是由10个大小完全相同的小正方体搭成的几何体的俯视图,小正方体上的数字为对应位置上小正方体的数量,将数字“3”上的小正方体向数字“2”上的位置平移一个,下面说法正确的是( )
A.主视图与俯视图不变 B.左视图与俯视图不变
C.主视图与左视图改变 D.三种视图都不变
7.小明同学拿着一个如图所示的三角形木架在太阳光下玩,他不断变换三角形木架的位置,他说他发现了三角形木架在地上出现过的影子有四种:①点;②线段;③三角形;④四边形.你认为小明说法中正确的个数有( )
A.4个 B.3个 C.2个 D.1个
8.长方体的主视图和左视图如图所示(单位:cm),则其俯视图的面积是( )
A.10cm2 B.12cm2 C.15cm2 D.20cm2
9.我们知道,面动成体!如图,正方形ABCD边长为3cm,以直线AB为轴将正方形旋转一周所得几何体,从正面看到的形状图的面积是( ).
A.9 cm2 B.18 cm2
C.9π cm2 D.27π cm2
10.由若干个相同的小立方体搭成的一个几何体的主视图和俯视图如图所示,俯视图的方格中的字母和数字表示该位置上小立方体的个数,则以下说法正确的是( )
A.x=1或2,y=3 B.x=1或2,y=1或3
C.x=1,y=1或3 D.x=2,y=1或3
11.圆桌面(桌面中间有一个直径为1m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为2m,桌面离地面1m,若灯泡离地面2m,则地面圆环形阴影的面积是( )
A.2πm2 B.3πm2 C.6πm2 D.12πm2
12.如图是一个圆锥的三视图,俯视图是直径为的圆,主视图和左视图都是底为,腰为的等腰三角形,这个圆锥的体积是=( )
A. B. C. D.
二、填空题:本题共6个小题,每小题3分,共18分。
13.广场上一个大型艺术字板块在地上的投影如图所示,则该投影属于_____.(填写“平行投影”或“中心投影”)
14.如图,一棵树(AB)的高度为7.5米,下午某一个时刻它在水平地面上形成的树影长(BE)为10米,现在小明想要站这棵树下乘凉,他的身高为1.5米,那么他最多可以离开树干多少米才可以不被阳光晒到?____.
15.如图,上、下底面为全等的正六边形礼盒,其主视图与左视图均由矩形构成,主视图中大矩形边长如图,左视图中包含两个全等的矩形,如果用彩色胶带按如图包扎礼盒,所需胶带长度至少为___________ cm.(精确到0.001 cm)
16.下面是由一些相同的小正方体构成的几何体从三个方向看到的图形,至少要_______个小正方体构成这个几何体.
17.如图是一个由若干个正方体搭建而成的几何体的主视图与左视图,那么下列图形中可以作为该几何体的俯视图的序号是________(多填或错填得0分,少填酌情给分).
18.如图,迎宾公园的喷水池边上有半圆形的石头(半径为1.12m)作为装饰,其中一块石头正前方5.88m处有一彩灯,某一时刻,该灯柱落在此半圆形石头上的影长为0.56πm.如果同一时刻,一直立0.6m的杆子的影长为1.8m,则灯柱的高____m.
三、解答题(19题6分,其余每题8分,共46分)
19.从棱长为2的正方体毛坯的一角,挖去一个棱长为1的小正方体,得到一个如图所示的零件.
(1)这个零件的表面积是 .
(2)请按要求在边长为1网格图里画出这个零件的视图.
20.如图1,国庆期间某广场旗杆附近搭建了一座花篮.图2为从该场景抽象出的数学模型,已知花篮高度,某一时刻花篮在阳光下的投影.
(1)请你用尺规作图法在图2中作出此时旗杆在阳光下的投影;(不写作法,保留作图痕迹)
(2)在测量的投影时,同时测出旗杆在阳光下的投影,请你计算的长.
21.如图,是某公园的一个圆形桌面的主视图,是该桌面在一路灯下的影子,是一个圆形凳面的主视图.(桌面、凳面均与地面平行)
(1)请标出路灯的位置,并画出在该路灯下的影子;(保留画图痕迹,光线用虚线表示)
(2)若桌面直径和桌面与地面的距离均为,并测得影子,求路灯与地面的距离.
22.一透明的敞口正方体容器装有一些液体,棱AB始终在水平桌面上,容器底部的倾斜角为α,(∠CBE=α,如图1所示),此时液面刚好过棱CD,并与棱BB'交于点Q,此时液体的形状为直三棱柱,三视图及尺寸如图2所示,求当正方体平放(正方形ABCD在桌面上)时,液体的深度.
23.如图,如图几何体是由若干棱长为1的小立方体按一定规律在地面上摆成的,若将露出的表面都涂上颜色(底面不涂色),观察该图,探究其中的规律.
(1)第1个几何体中只有2个面涂色的小立方体共有 个;第2个几何体中只有2个面涂色的小立方体共有 个;第3个几何体中只有2个面涂色的小立方体共有 个.
(2)求出第10个几何体中只有2个面涂色的小立方体的块数.
(3)求出前100个几何体中只有2个面涂色的小立方体的块数的和.
24.图1至图7中的网格图均是20×20的等距网格图(每个小方格的边长均为1个单位长).侦察兵王凯在P点观察区域MNCD内的活动情况.当5个单位长的列车(图中的)以每秒1个单位长的速度在铁路线MN上通过时,列车将阻挡王凯的部分视线,在区域MNCD内形成盲区(不考虑列车的宽度和车厢间的缝隙).设列车车头运行到M点的时刻为0,列车从M点向N点方向运行的时间为t(秒).
(1)在区域MNCD内,请你针对图1,图2,图3,图4中列车位于不同位置的情形分别画出相应的盲区,并在盲区内涂上阴影.
(2)只考虑在区域ABCD内开成的盲区.设在这个区域内的盲区面积是y(平方单位).
①如图5,当5≤t≤10时,请你求出用t表示y的函数关系式;
②如图6,当10≤t≤15时,请你求出用t表示y的函数关系式;
③如图7,当15≤t≤20时,请你求出用t表示y的函数关系式;
④根据①~③中得到的结论,请你简单概括y随t的变化而变化的情况.
(3)根据上述研究过程,请你按不同的时段,就列车行驶过程中在区域MNCD内所形成盲区的面积大小的变化情况提出一个综合的猜想.
答案
一、选择题。
A.B.B.B.B.B.C.B.B.A.B.A
二、填空题。
13.中心投影
14.8.
15.431.769.
16.7
17.①②③
18.(m).
三、解答题
19.
解:(1)2×2×6=24.
这个零件的表面积是24,
故答案为:24.
(2)如图所示:
20.
解:(1)如图就是的投影.
(2)由作图可知,
,
,
∴△ABC∽△DEF,
,即,
.
答:的长为.
21.
解:(1)如图,路灯和线段即为所画.
(2)如图,过点作,交于点,
∵,
∴,,.
∴∽,
∴.
∵,,,
∴,
∴.
答:路灯与地面的距离为.
22.
解:∵CQ=5dm,AB=4dm,
是正方体
∴BQ===3(dm),
∴液体的体积为:V液=×3×4×4=24(dm3),
正方形的面积为
∴液体的深度是24÷16=1.5(dm).
23.
解:(1)观察图形可知:图①中,两面涂色的小立方体共有4个;
图②中,两面涂色的小立方体共有12个;
图③中,两面涂色的小立方体共有20个;
故答案为:4,12,20;
(2)观察图形可知:图①中,只有2个面涂色的小立方体共有4个;
图②中,只有2个面涂色的小立方体共有12个;
图③中,只有2个面涂色的小立方体共有20个.
4,12,20都是4的倍数,可分别写成4×1,4×3,4×5的形式,
因此,第n个图中两面涂色的小立方体共有4(2n-1)=8n-4,
则第100个几何体中只有2个面涂色的小立方体共有8×100-4=796个;
(3)(8×1-4)+(8×2-4)+(8×3-4)+(8×4-4)+(8×5-4)+…+(8×100-4)
=8×(1+2+3+4+…+100)-100×4
=40000(个).
故前100个几何体中只有2个面涂色的小立方体的个数的和为40000个.
24.
(1)在P视点看不见的列车后的区域就是盲区,也就是过P和列车的两端的射线交CD于两点,这两点和列车两端构成的梯形就是所指的盲区.如图1的梯形AA1D1D,图2的梯形A2B2C2D2,图3的梯形B3BCC3.
(2)①如图1,当5≤t≤10时,盲区是梯形AA1D1D
∵O是PQ中点,且OA∥QD,
∴A1,A分别是PD1和PD中点
∴A1A是△PD1D的中位线.
又∵A1A=t-5,∴D1D=2(t-5)
而梯形AA1D1D的高OQ=10,
∴y= [(t-5)+2(t-5)]×10=15t-75
∴y=15t-75.
②如图2,当10≤t≤15时,盲区是梯形A2B2C2D2,
易知A2B2是△PC2D2的中位线,且A2B2=5,
∴C2D2=10
又∵梯形A2B2C2D2的高OQ=10,
∴y=(5+10)×10=75
∴y=75.
③如图3,当15≤t≤20时,盲区是梯形B3BCC3
易知BB3是△PCC3的中位线
且BB3=5-(t-15)=20-t
又∵梯形B3BCC3的高OQ=10,
∴y= [(20-t)+2(20-t)]×10=300-15t
∴y=300-15t.
④当5≤t≤10时,由一次函数y=15t-75的性质可知,盲区的面积由0逐渐增大到75;
当10≤t≤15时,盲区的面积y为定值75;
当15≤t≤20时,由一次函数y=300-15t的性质可知,盲区的面积由75逐渐减小到0.
(3)通过上述研究可知,列车从M点向N点方向运行的过程中,在区域MNCD内盲区面积大小的变化是:
①在0≤t≤10时段内,盲区面积从0逐渐增大到75;
②在10≤t≤15时段内,盲区的面积为定值75;
③在15≤t≤20时段内,盲区面积从75逐渐减小到0.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
