等腰三角形[上学期]
图片预览




文档简介
课件14张PPT。14.3.1
等腰三角形乌市第六十五中学 孙华
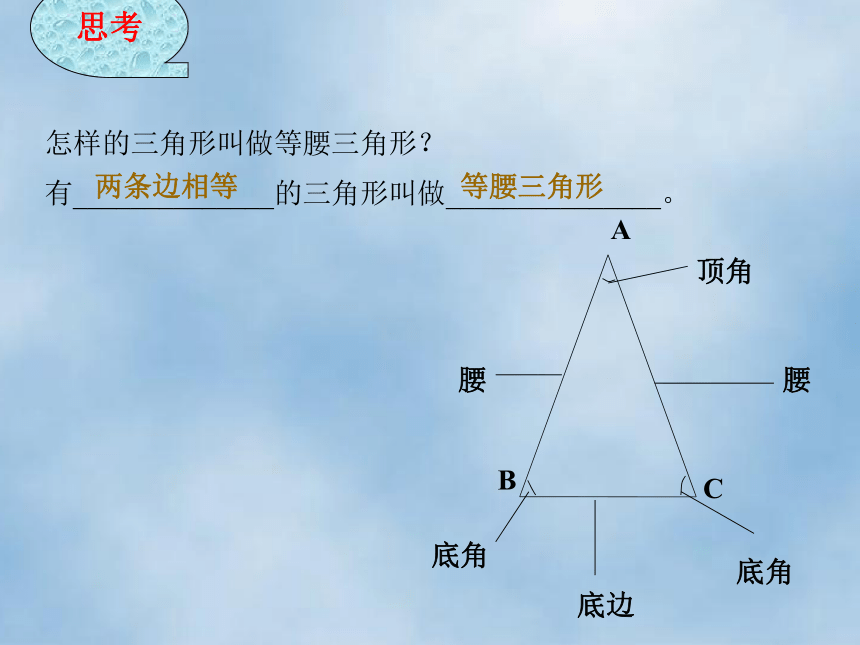
2006.4探究 如图14.3-1,把一张长方形的纸按图中虚线对折,并减去阴影部分,再把它展开得到的 △ABC有什么特点? 怎样的三角形叫做等腰三角形?有______________的三角形叫做_______________。思考两条边相等等腰三角形思考?上面剪出的三角形是等腰三角形吗?
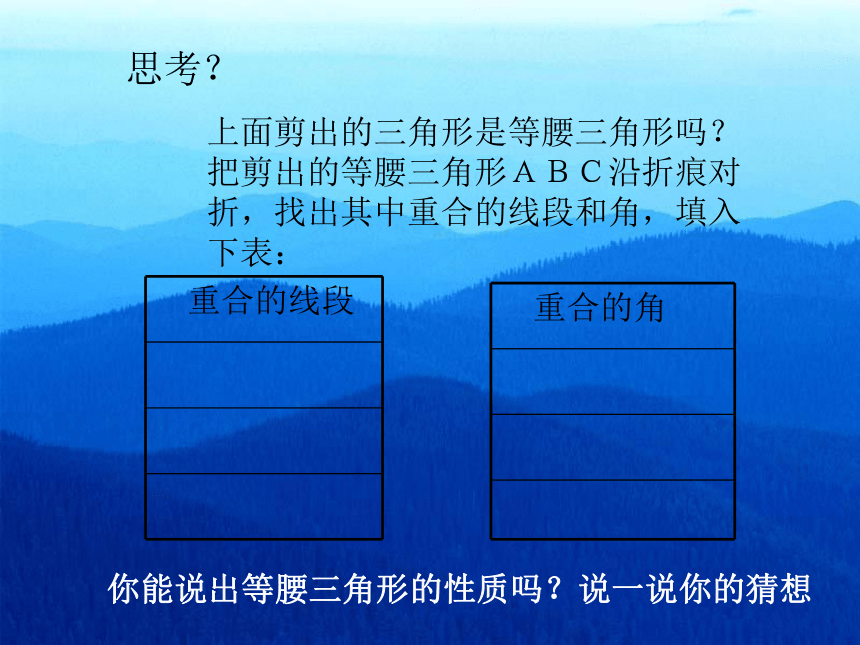
把剪出的等腰三角形ABC沿折痕对
折,找出其中重合的线段和角,填入
下表:你能说出等腰三角形的性质吗?说一说你的猜想性质1
等腰三角形的两个底角相等(简写成"等边对等角")性质2
等腰三角形的顶角平分线、底边
上的中线、底边上的高相互重合等腰三角形的性质
1 等腰三角形的两个底角相等(等边对等角)
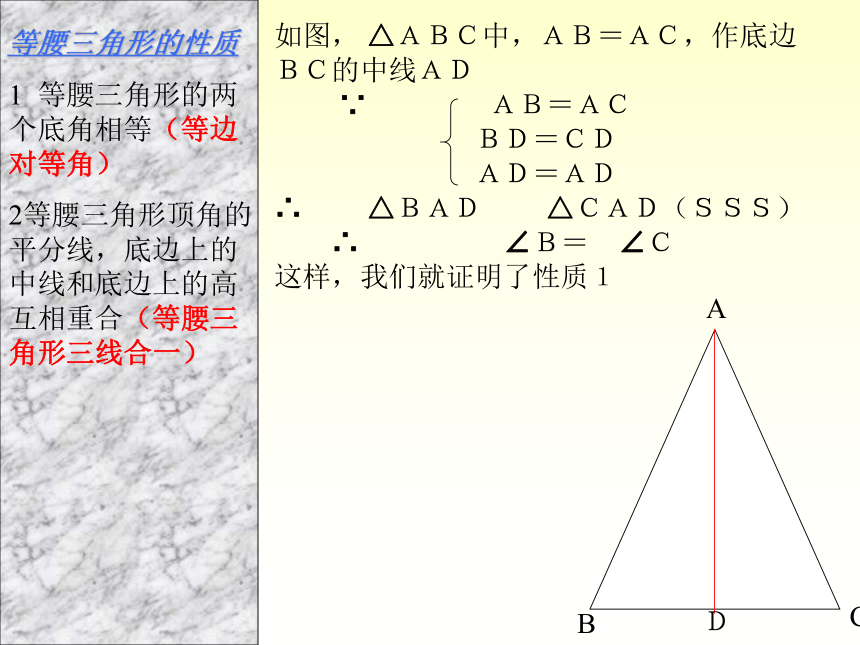
2等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)如图, △ABC中,AB=AC,作底边 BC的中线AD
∵ AB=AC
BD=CD
AD=AD
∴ △BAD △CAD(SSS)
∴ ∠B= ∠C
这样,我们就证明了性质1
D等腰三角形的性质
1 等腰三角形的两个底角相等(等边对等角)
2等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)
? 思考
受性质1证明的启发,你能证明性质2吗?等腰三角形的性质
1 等腰三角形的两个底角相等(等边对等角)
2等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)
(1)如图1,等腰三角形的顶角是36°,则它的底角是 度。
(2)在△ABC中,AB=AC,∠BAC=90°,AD是BC边上的高,∠BAD=____,BD=_______=__________.
(1)D等腰三角形的性质
1 等腰三角形的两个底角相等(等边对等角)
2等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)例1 如图:在△ABC中,AB=AC,点D在AC上,且BC=AD=BD,求△ABC各角的度数。解:∵AB=AC,BC=AD=BD)∴∠ABC=∠C=∠BDC
∠A=∠ABD (等边对等角)设∠A=x,则∠BDC=∠A+∠ABD=2X从而∠ABC=∠C=∠BDC=2X 于是在△ABC中,有
∠A+∠ABC+∠C=X+2X+2X=180 °解得 X=36 °在△ABC中,∠A=36 ° ,∠ABC=∠C=72°(四)感悟收获
通过本节课的探索研究,你收获到了什么?有何感受?(五)布置作业:
1、课本P149-150习题14.3 1(必作),3(必作),7(选作)
2、实验感悟(选作):画线段BC,分别以B、C为顶点作两个相等的角,两角终边的交点为A,再作△ABC的中线AD,然后沿AD翻折,试试看你有新的发现吗? 七、设计说明
1、本设计始终体现以学生为中心的教育理念,通过数学实验激发了学生探究的兴趣,提高了他们实验、分析、探究的能力,让学生体会到实验观察、猜想、归纳、验证的思想和数形结合的思想,学生的创造力得到充分发挥,从而得出新的结论和新的猜想,因为教学过程也就是学生的认知过程,只有学生积极参与才能达到教学目的,同时遵循学生学习数学的心理规律,让学生在一定情景中去经历、感悟知识,才是学生最有价值的收获,体现了学生从维持性学习走向研究性学习,从而走向自主创新性学习的转变和进步。2板书设计:投影屏幕 概念 例题
定理
证明 练习
3时间安排:
“复习引入” 约3分钟, “探索、发现、验证过程”约17分钟。 “技能演练与拓展”约20分钟。“感悟收获”约4分钟,“布置作业”约1分钟。
(注: 45分钟一课时) 再见
等腰三角形乌市第六十五中学 孙华
2006.4探究 如图14.3-1,把一张长方形的纸按图中虚线对折,并减去阴影部分,再把它展开得到的 △ABC有什么特点? 怎样的三角形叫做等腰三角形?有______________的三角形叫做_______________。思考两条边相等等腰三角形思考?上面剪出的三角形是等腰三角形吗?
把剪出的等腰三角形ABC沿折痕对
折,找出其中重合的线段和角,填入
下表:你能说出等腰三角形的性质吗?说一说你的猜想性质1
等腰三角形的两个底角相等(简写成"等边对等角")性质2
等腰三角形的顶角平分线、底边
上的中线、底边上的高相互重合等腰三角形的性质
1 等腰三角形的两个底角相等(等边对等角)
2等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)如图, △ABC中,AB=AC,作底边 BC的中线AD
∵ AB=AC
BD=CD
AD=AD
∴ △BAD △CAD(SSS)
∴ ∠B= ∠C
这样,我们就证明了性质1
D等腰三角形的性质
1 等腰三角形的两个底角相等(等边对等角)
2等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)
? 思考
受性质1证明的启发,你能证明性质2吗?等腰三角形的性质
1 等腰三角形的两个底角相等(等边对等角)
2等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)
(1)如图1,等腰三角形的顶角是36°,则它的底角是 度。
(2)在△ABC中,AB=AC,∠BAC=90°,AD是BC边上的高,∠BAD=____,BD=_______=__________.
(1)D等腰三角形的性质
1 等腰三角形的两个底角相等(等边对等角)
2等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)例1 如图:在△ABC中,AB=AC,点D在AC上,且BC=AD=BD,求△ABC各角的度数。解:∵AB=AC,BC=AD=BD)∴∠ABC=∠C=∠BDC
∠A=∠ABD (等边对等角)设∠A=x,则∠BDC=∠A+∠ABD=2X从而∠ABC=∠C=∠BDC=2X 于是在△ABC中,有
∠A+∠ABC+∠C=X+2X+2X=180 °解得 X=36 °在△ABC中,∠A=36 ° ,∠ABC=∠C=72°(四)感悟收获
通过本节课的探索研究,你收获到了什么?有何感受?(五)布置作业:
1、课本P149-150习题14.3 1(必作),3(必作),7(选作)
2、实验感悟(选作):画线段BC,分别以B、C为顶点作两个相等的角,两角终边的交点为A,再作△ABC的中线AD,然后沿AD翻折,试试看你有新的发现吗? 七、设计说明
1、本设计始终体现以学生为中心的教育理念,通过数学实验激发了学生探究的兴趣,提高了他们实验、分析、探究的能力,让学生体会到实验观察、猜想、归纳、验证的思想和数形结合的思想,学生的创造力得到充分发挥,从而得出新的结论和新的猜想,因为教学过程也就是学生的认知过程,只有学生积极参与才能达到教学目的,同时遵循学生学习数学的心理规律,让学生在一定情景中去经历、感悟知识,才是学生最有价值的收获,体现了学生从维持性学习走向研究性学习,从而走向自主创新性学习的转变和进步。2板书设计:投影屏幕 概念 例题
定理
证明 练习
3时间安排:
“复习引入” 约3分钟, “探索、发现、验证过程”约17分钟。 “技能演练与拓展”约20分钟。“感悟收获”约4分钟,“布置作业”约1分钟。
(注: 45分钟一课时) 再见
