等腰三角形的性质[下学期]
图片预览



文档简介
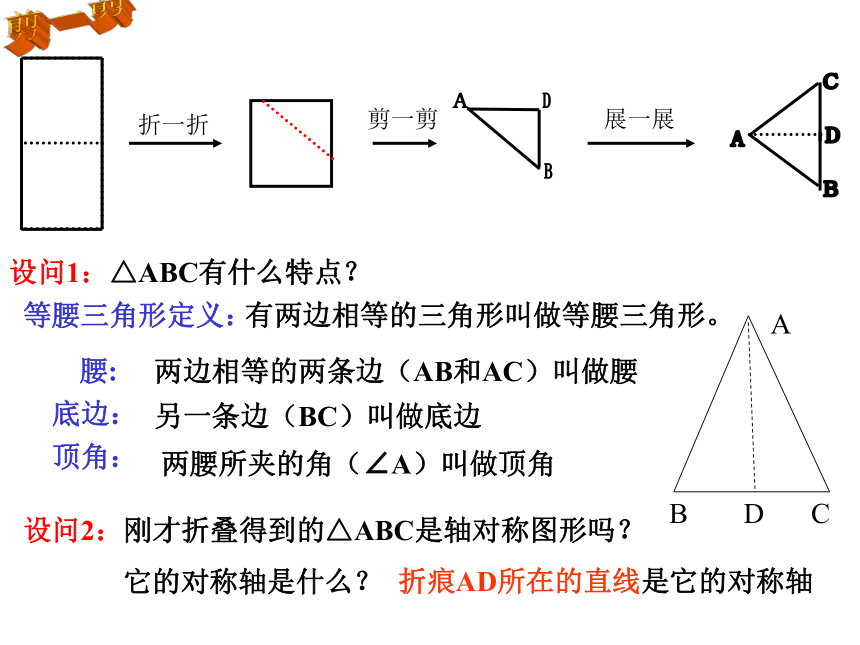
课件13张PPT。等腰三角形的性质设问1:△ABC有什么特点? 等腰三角形定义:有两边相等的三角形叫做等腰三角形。两边相等的两条边(AB和AC)叫做腰另一条边(BC)叫做底边两腰所夹的角(∠A)叫做顶角剪一剪设问2:刚才折叠得到的△ABC是轴对称图形吗?
它的对称轴是什么?折痕AD所在的直线是它的对称轴 设问3:由折叠,你能发现等腰三角形有什么性质?
① ∠B = ∠C
② BD = CD
③ ∠BAD=∠CDA
④∠ADC= ∠ADB=900
⑤ AB=AC等腰三角形性质:
性质1 等腰三角形的两个底角相等。性质2 等腰三角形的顶角平分线、底边上的中线、底 边
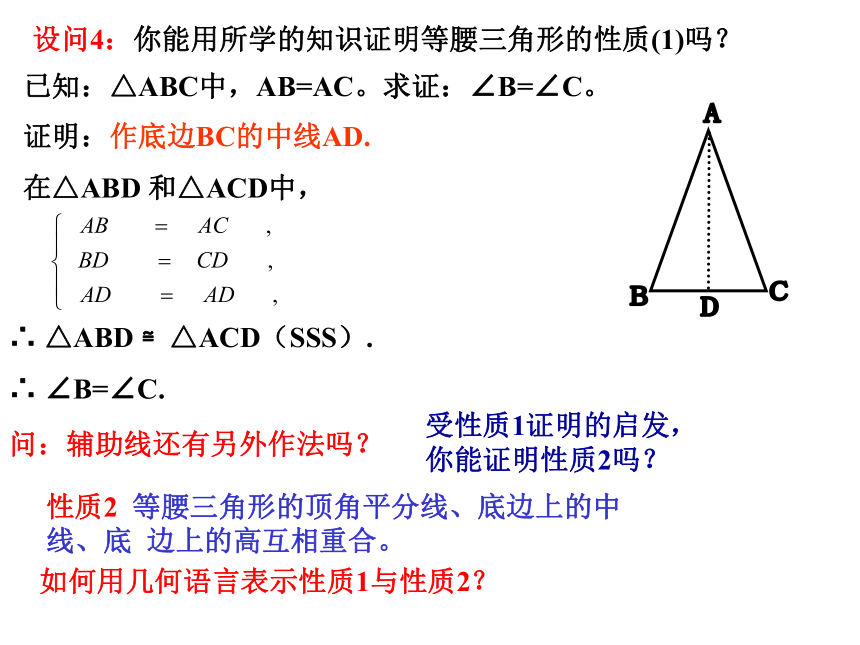
上的高互相重合。(可简记为“三线合一”)(简写成“等边对等角”);→ 两个底角相等→ AD为底边BC上的中线→ AD为顶角∠BAC的平分线→ AD为底边BC上的高→ 等腰三角形的两腰相等设问4:你能用所学的知识证明等腰三角形的性质(1)吗? 已知:△ABC中,AB=AC。求证:∠B=∠C。证明:作底边BC的中线AD.
在△ABD 和△ACD中,∴ △ABD ≌△ACD(SSS).
∴ ∠B=∠C.受性质1证明的启发,你能证明性质2吗?问:辅助线还有另外作法吗? 如何用几何语言表示性质1与性质2?性质2 等腰三角形的顶角平分线、底边上的中线、底 边上的高互相重合。等腰三角形性质:
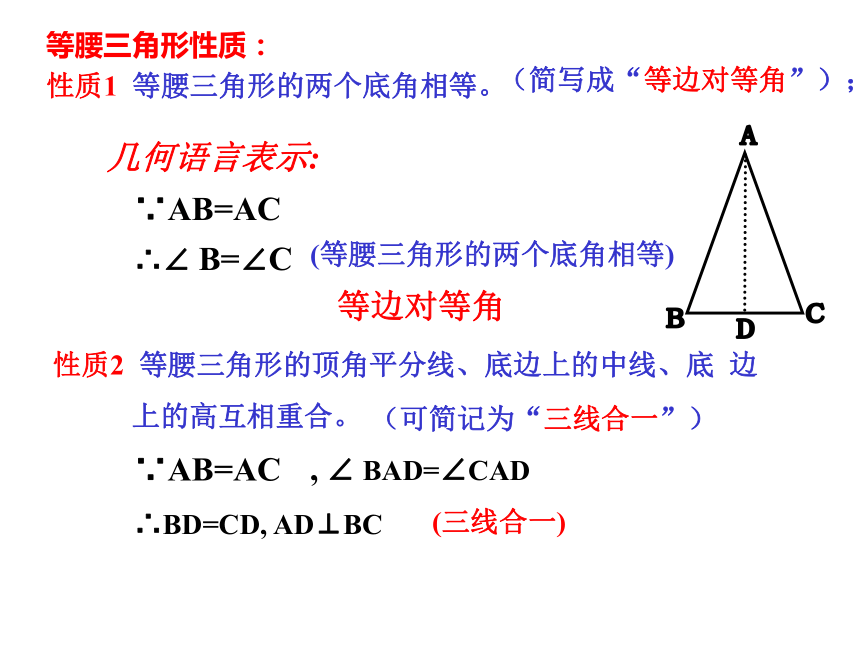
性质1 等腰三角形的两个底角相等。性质2 等腰三角形的顶角平分线、底边上的中线、底 边
上的高互相重合。(可简记为“三线合一”)(简写成“等边对等角”);几何语言表示:∵AB=AC∴∠ B=∠C (等腰三角形的两个底角相等)∵AB=AC, ∠ BAD=∠CAD ∴BD=CD, AD⊥BC (三线合一)等边对等角 在等腰三角形中,
(1)已知顶角为70°,其余两个角分别为__。
(2)已知底角为70°,其余两个角分别为__。 (3)已知一个角为70°, 其余两个角分别为__
(4)已知一个角为100°,其余两个角分别为_(5)已知等腰三角形的两边长分别是4和6,则它的周长是( )
A、14 B、15 C、16 D、14或16
55°,55°70°,40° 例1、在△ABC中,AB=AC,点D在AC上,且BD=BC=AD。
(1)图中共有几个等腰三角形?分别写出它们的顶角和底角。
(2)你能求出△ABC各角的度数吗? 练习: 已知:如图,房屋的顶角∠BAC=100 o, 过屋顶A的立柱AD ? BC , 屋椽AB=AC. 求顶架上∠B、∠C、∠BAD、
∠CAD的度数.
∴∠BAD=∠CAD=50°ABCD已知:如图,AB=BC=CD=ED=EF.EFMN∠A=15°,试求∠ FEM的度数? 已知:点D、E在△ABC中, AB=AC,AD=AE. 求证:BD=CE。ABCDE猜想一下,等腰三角形底边中点到两腰的距离相等吗?(高DE=DF?)(中线DE=DF?)(角平线DE=DF?)1、研究有关等腰三角形的问题,
顶角平分线、底边中线,底边的
高是常用的辅助线;2、熟练求解等腰三角形的顶
角、底角的度数;
共同特点
它的对称轴是什么?折痕AD所在的直线是它的对称轴 设问3:由折叠,你能发现等腰三角形有什么性质?
① ∠B = ∠C
② BD = CD
③ ∠BAD=∠CDA
④∠ADC= ∠ADB=900
⑤ AB=AC等腰三角形性质:
性质1 等腰三角形的两个底角相等。性质2 等腰三角形的顶角平分线、底边上的中线、底 边
上的高互相重合。(可简记为“三线合一”)(简写成“等边对等角”);→ 两个底角相等→ AD为底边BC上的中线→ AD为顶角∠BAC的平分线→ AD为底边BC上的高→ 等腰三角形的两腰相等设问4:你能用所学的知识证明等腰三角形的性质(1)吗? 已知:△ABC中,AB=AC。求证:∠B=∠C。证明:作底边BC的中线AD.
在△ABD 和△ACD中,∴ △ABD ≌△ACD(SSS).
∴ ∠B=∠C.受性质1证明的启发,你能证明性质2吗?问:辅助线还有另外作法吗? 如何用几何语言表示性质1与性质2?性质2 等腰三角形的顶角平分线、底边上的中线、底 边上的高互相重合。等腰三角形性质:
性质1 等腰三角形的两个底角相等。性质2 等腰三角形的顶角平分线、底边上的中线、底 边
上的高互相重合。(可简记为“三线合一”)(简写成“等边对等角”);几何语言表示:∵AB=AC∴∠ B=∠C (等腰三角形的两个底角相等)∵AB=AC, ∠ BAD=∠CAD ∴BD=CD, AD⊥BC (三线合一)等边对等角 在等腰三角形中,
(1)已知顶角为70°,其余两个角分别为__。
(2)已知底角为70°,其余两个角分别为__。 (3)已知一个角为70°, 其余两个角分别为__
(4)已知一个角为100°,其余两个角分别为_(5)已知等腰三角形的两边长分别是4和6,则它的周长是( )
A、14 B、15 C、16 D、14或16
55°,55°70°,40° 例1、在△ABC中,AB=AC,点D在AC上,且BD=BC=AD。
(1)图中共有几个等腰三角形?分别写出它们的顶角和底角。
(2)你能求出△ABC各角的度数吗? 练习: 已知:如图,房屋的顶角∠BAC=100 o, 过屋顶A的立柱AD ? BC , 屋椽AB=AC. 求顶架上∠B、∠C、∠BAD、
∠CAD的度数.
∴∠BAD=∠CAD=50°ABCD已知:如图,AB=BC=CD=ED=EF.EFMN∠A=15°,试求∠ FEM的度数? 已知:点D、E在△ABC中, AB=AC,AD=AE. 求证:BD=CE。ABCDE猜想一下,等腰三角形底边中点到两腰的距离相等吗?(高DE=DF?)(中线DE=DF?)(角平线DE=DF?)1、研究有关等腰三角形的问题,
顶角平分线、底边中线,底边的
高是常用的辅助线;2、熟练求解等腰三角形的顶
角、底角的度数;
共同特点
