4.3.2 独立性检验 同步练习——2022-2023学年高二上学期数学人教B版(2019)选择性必修第二册(含答案)
文档属性
| 名称 | 4.3.2 独立性检验 同步练习——2022-2023学年高二上学期数学人教B版(2019)选择性必修第二册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 187.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-20 15:58:19 | ||
图片预览




文档简介
4.3.2 独立性检验——2022-2023学年高二数学人教B版(2019)选择性必修第二册同步课时训练
一、概念练习
1.某校随机调查了110名不同的高中生是否喜欢篮球,得到如下的列联表:
男 女
喜欢篮球 40 20
不喜欢篮球 20 30
附:
0.050 0.010 0.001
3.841 6.635 10.828
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过0.1%的前提下,认为“喜欢篮球与性别有关”
B.在犯错误的概率不超过0.1%的前提下,认为“喜欢篮球与性别无关”
C.有99%以上的把握认为“喜欢篮球与性别有关”
D.有99%以上的把握认为“喜欢篮球与性别无关”
2.第24届冬季奥林匹克运动会将于2022年在北京举办.为了解某城市居民对冰雪运动的关注情况,随机抽取了该市100人进行调查统计,得到如下列联表.
男 女 合计
关注冰雪运动 35 25 60
不关注冰雪运动 15 25 40
合计 50 50 100
参考公式:,其中.
附表:
0.100 0.050 0.010 0.001
2.706 3.841 6.635 10.828
根据列联表可知( )
A.该市女性居民中大约有的人关注冰雪运动
B.该市男性届民中大约有的人关注冰雪运动
C.有的把握认为该市居民是否关注冰雪运动与性别有关
D.有的把握认为该市居民是否关注冰雪运动与性别有关
3.已知两个分类变量X与Y,它们的列联表如下:
总计
10 21 31
c d 35
总计 66
若有90%的把握认为X与Y有关系,则( )
附:
0.1 0.05 0.01 0.005 0.001
k 2.706 3.841 6.635 7.879 10.828
A.4 B.5 C.6 D.7
4.某品牌公司在海外设立了多个分支机构,现需要国内公司外派大量中、青年员工该企业为了解这两个年龄层的员工是否愿意被外派,采用分层抽样的方法从中、青年员工中随机抽取了100位进行调查,得到数据如下表:
愿意被外派 不愿意被外派 总计
中年员工 20 30 50
青年员工 40 10 50
总计 60 40 100
得到的正确结论是( )
A.有90%的把握认为“是否愿意被外派与年龄有关”
B.有90%的把握认为“是否愿意被外派与年龄无关”
C.有99%的把握认为“是否愿意被外派与年龄有关”
D.有99%的把握认为“是否愿意被外派与年龄无关”
5.某研究所为了检验新开发的疫苗对某疾病的预防作用,对1000名注射了疫苗的人与另外1000名未注射疫苗的人的一年健康记录进行比较,并提出假设:这种疫苗不能起到预防该疾病的作用,并计算出,则下列说法正确的是( )
A.这种疫苗能起到预防该疾病的作用的有效率为1%
B.若某人未使用该疫苗,则他在半年内有99%的可能性得该疾病
C.有1%的把握认为这种疫苗能起到预防该疾病的作用
D.有99%的把握认为这种疫苗能起到预防该疾病的作用
二、能力提升
6.某组织为研究爱好某项运动是否与性别有关进行了一个调查,得到如下列联表,若这两个变量没有关系,则a的可能值为( )
男性 女性 总计
爱好 100 a
不爱好 120 600 720
总计 220
A.720 B.500 C.300 D.200
7.对于分类变量X与Y的统计量,下列说法正确的是( )
A.越大,“X与Y有关系”的可信程度越小
B.越小,“X与Y有关系”的可信程度越小
C.越接近于0,“X与Y没有关系”的可信程度越小
D.越大,“X与Y没有关系”的可信程度越大
8. (多选)某校对“学生性别和喜欢锻炼是否有关”作了一次调查,其中被调查的男女生人数相同,男生喜欢锻炼的人数占男生总人数的,女生喜欢锻炼的人数占女生总人数的.若至少有95%的把握认为“学生性别和喜欢锻炼有关”,则被调查学生中男生的人数可能为( )
附:
0.050 0.010
3.841 6.635
A.35 B.40 C.45 D.50
9. (多选)有关独立性检验的四个命题,其中正确的是( )
A.两个变量的2×2列联表中,对角线上数据的乘积相差越大,说明两个变量有关系的可能性就越大
B.对分类变量X与Y的随机变量来说,越小,“X与Y有关系”的可信程度越小
C.从独立性检验可知:有95%的把握认为秃顶与患心脏病有关,我们说某人秃顶,那么他有95%的可能患有心脏病
D.从独立性检验可知:有99%的把握认为吸烟与患肺癌有关,是指在犯错误的概率不超过1%的前提下,认为吸烟与患肺癌有关
10. (多选)下列四个命题不正确的是( )
A.由独立性检验可知,有9%的把握认为物理成绩与数学成绩有关,若某人数学成绩优秀,则他的物理成绩一定优秀
B.两个随机变量相关性越强,则相关系数的绝对值越接近于0
C.在线性回归方程中,当变量每增加1个单位时,变量增加0.2个单位
D.线性回归直线至少经过其样本数据点中的一个点
11.2020年世界各地相继出现新冠疫情,这已经成为全球性的公共卫生问题.为了测试某种新冠疫苗的效果,某实验室随机抽取100只健康小鼠进行试验,得到如下列联表:
感染 未感染 总计
注射 10 40 50
未注射 20 30 50
总计 30 70 100
则在犯错误的概率不超过______________的前提下,可认为“注射疫苗”与“感染新冠肺炎”有关系.
附:,其中.
0.1 0.05 0.01 0.005 0.001
2.706 3.841 6.635 7.879 10.828
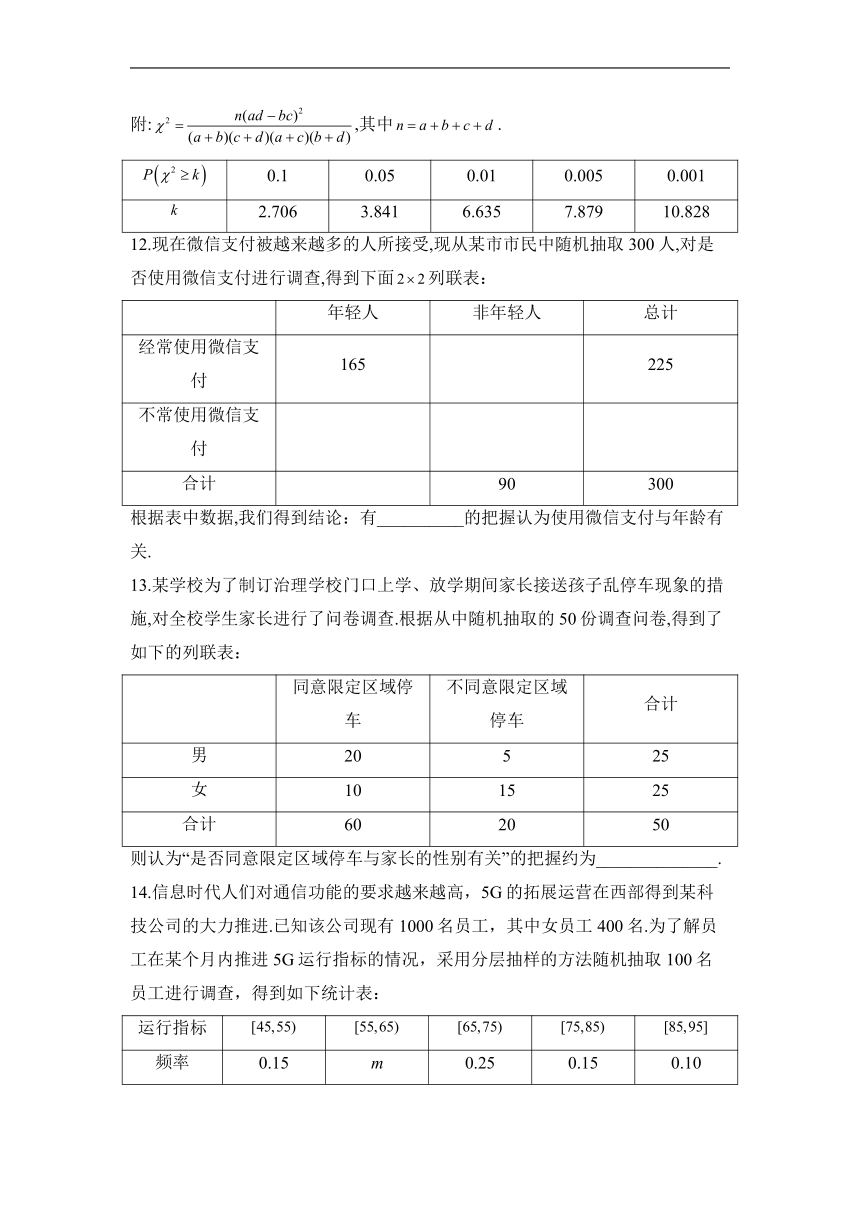
12.现在微信支付被越来越多的人所接受,现从某市市民中随机抽取300人,对是否使用微信支付进行调查,得到下面列联表:
年轻人 非年轻人 总计
经常使用微信支付 165 225
不常使用微信支付
合计 90 300
根据表中数据,我们得到结论:有__________的把握认为使用微信支付与年龄有关.
13.某学校为了制订治理学校门口上学、放学期间家长接送孩子乱停车现象的措施,对全校学生家长进行了问卷调查.根据从中随机抽取的50份调查问卷,得到了如下的列联表:
同意限定区域停车 不同意限定区域停车 合计
男 20 5 25
女 10 15 25
合计 60 20 50
则认为“是否同意限定区域停车与家长的性别有关”的把握约为______________.
14.信息时代人们对通信功能的要求越来越高,5G的拓展运营在西部得到某科技公司的大力推进.已知该公司现有1000名员工,其中女员工400名.为了解员工在某个月内推进5G运行指标的情况,采用分层抽样的方法随机抽取100名员工进行调查,得到如下统计表:
运行指标
频率 0.15 m 0.25 0.15 0.10
(1)求m的值,并估计该科技公司该月推进5G运行指标的平均数(同一组中的数据用该组区间的中点值为代表);
(2)若将推进5G运行指标不低于75的员工评为“璀璨之星”,已知该月被评为“璀璨之星”的男员工有10人,完成如下2×2列联表,并且判断是否有97.5%的把握认为被评为“璀璨之星”与性别有关.
“璀璨之星” 非“璀璨之星” 合计
男员工
女员工
合计
附:.
0.150 0.100 0.050 0.025 0.010
k 2.072 2.706 3.841 5.024 6.635
15.某食品专卖店为调查某种零售食品的受欢迎程度,通过电话回访的形式,随机调查了200名年龄在岁的顾客.以28岁为分界线,按喜欢不喜欢,得到下表,且年龄在岁间不喜欢该食品的频率是.
喜欢 不喜欢 合计
年龄岁(含28岁) 80 m
年龄岁(含40岁) n 40
合计
(I)求表中m,n的值;
(Ⅱ)能否有的把握认为顾客是否喜欢该食品与年龄有关?
附:,其中.
0.050 0.010 0.001
k 3.841 6.635 10.828
答案以及解析
1.答案:C
解析:由题意,,因此有99%以上的把握认为“喜欢篮球与性别有关”.
故选:C.
2.答案:C
解析:由列联表中的数据可得,因此,有的把握认为该市居民是否关注冰雪运动与性别有关.故选:C.
3.答案:B
解析:有90%的把握认为X与Y有关系,,,将选项代入检验,得符合题意.
4.答案:C
解析:由题意,可得,所以有99%的把握认为“是否愿意被外派与年龄有关”,故选C.
5.答案:D
解析:由,可知D正确.
6.答案:B
解析:结合选项,知当时,,所以这两个变量没有关系,故选B.
7.答案:B
解析:根据统计量的意义,知只有B正确.
8.答案:CD
解析:解:由题意被调查的男女生人数相同,设男生的人数为:5n,,由题意可列出列联表:
男生 女生 合计
喜欢锻炼 4n 3n 7n
不喜欢锻炼 n 2n 3n
合计 5n 5n 10n
.
由于有95%的把握认为“学生性别和喜欢锻炼有关”,所以;
解得:,则n的可能取值为:9、10、11、12、13;
则选项中被调查学生中男生的人数可能45或50.
故选:CD.
9.答案:ABD
解析:两个变量的2×2列联表中,对角线上数据的乘积相差越大,则越大,两个变量有关系的可能性越大,所以选项A正确;根据越小,则“X与Y有关系”的可信度越小,所以选项B正确;从独立性检验可知,有95%的把握认为秃顶与患心脏病有关,不表示某人秃顶他有95%的可能患有心脏病,所以选项C不正确;从独立性检验可知,有99%的把握认为吸烟与患肺癌有关,是指在犯错误的概率不超过1%的前提下,认为吸烟与患肺癌有关,是独立性检验的解释,所以选项D正确.故选ABD.
10.答案:ABD
解析:由独立性检验可知,他的物理成绩不一定优秀,故A命题不正确;两个随机变量相关性越强,则相关系数的绝对值越接近于1,故B命题不正确;线性回归直线可能不经过其样本数据点中的任何点,故D命题不正确;易知C命题正确.故选ABD.
11.答案:0.05
解析:由题意得,所以在犯错误的概率不超过0.05的前提下,可认为“注射疫苗”与“感染新冠肺炎”有关系.
12.答案:95%
解析:由条件可得列联表:
年轻人 非年轻人 总计
经常使用微信支付 165 60 225
不常使用微信支付 45 30 75
合计 210 90 300
有95%的把握认为使用微信支付与年龄有关.
13.答案:99.5%
解析:因为,又,所以我们有99.5%的把握认为“是否同意限定区域停车与家长的性别有关”.
14.答案:(1),平均数约为67.
(2)有97.5%的把握认为被评为“璀璨之星”与性别有关.
解析:(1)根据题意,,解得,
平均数.
所以该科技公司该月推进5G运行指标的平均数约为67.
(2)根据题意,利用分层抽样法可知所抽取的100人中男员工60人,女员工40人,被评为“璀璨之星”的有(人),则被评为“璀璨之星”的女员工有(人),
则2×2列联表如下:
“璀璨之星” 非“璀璨之星” 合计
男员工 10 50 60
女员工 15 25 40
合计 25 75 100
则.
所以有97.5%的把握认为被评为“璀璨之星”与性别有关.
15.答案:(1),(2)有
解析:(1)由题中表格中数据可得
,解得,
且,解得.
(2)由(1)可补充列联表为
喜欢 不喜欢 合计
年龄岁(含28岁) 80 20 100
年龄岁(含40岁) 60 40 100
合计 140 60 200
则,
所以有的把握认为顾客是否喜欢该食品与年龄有关.
一、概念练习
1.某校随机调查了110名不同的高中生是否喜欢篮球,得到如下的列联表:
男 女
喜欢篮球 40 20
不喜欢篮球 20 30
附:
0.050 0.010 0.001
3.841 6.635 10.828
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过0.1%的前提下,认为“喜欢篮球与性别有关”
B.在犯错误的概率不超过0.1%的前提下,认为“喜欢篮球与性别无关”
C.有99%以上的把握认为“喜欢篮球与性别有关”
D.有99%以上的把握认为“喜欢篮球与性别无关”
2.第24届冬季奥林匹克运动会将于2022年在北京举办.为了解某城市居民对冰雪运动的关注情况,随机抽取了该市100人进行调查统计,得到如下列联表.
男 女 合计
关注冰雪运动 35 25 60
不关注冰雪运动 15 25 40
合计 50 50 100
参考公式:,其中.
附表:
0.100 0.050 0.010 0.001
2.706 3.841 6.635 10.828
根据列联表可知( )
A.该市女性居民中大约有的人关注冰雪运动
B.该市男性届民中大约有的人关注冰雪运动
C.有的把握认为该市居民是否关注冰雪运动与性别有关
D.有的把握认为该市居民是否关注冰雪运动与性别有关
3.已知两个分类变量X与Y,它们的列联表如下:
总计
10 21 31
c d 35
总计 66
若有90%的把握认为X与Y有关系,则( )
附:
0.1 0.05 0.01 0.005 0.001
k 2.706 3.841 6.635 7.879 10.828
A.4 B.5 C.6 D.7
4.某品牌公司在海外设立了多个分支机构,现需要国内公司外派大量中、青年员工该企业为了解这两个年龄层的员工是否愿意被外派,采用分层抽样的方法从中、青年员工中随机抽取了100位进行调查,得到数据如下表:
愿意被外派 不愿意被外派 总计
中年员工 20 30 50
青年员工 40 10 50
总计 60 40 100
得到的正确结论是( )
A.有90%的把握认为“是否愿意被外派与年龄有关”
B.有90%的把握认为“是否愿意被外派与年龄无关”
C.有99%的把握认为“是否愿意被外派与年龄有关”
D.有99%的把握认为“是否愿意被外派与年龄无关”
5.某研究所为了检验新开发的疫苗对某疾病的预防作用,对1000名注射了疫苗的人与另外1000名未注射疫苗的人的一年健康记录进行比较,并提出假设:这种疫苗不能起到预防该疾病的作用,并计算出,则下列说法正确的是( )
A.这种疫苗能起到预防该疾病的作用的有效率为1%
B.若某人未使用该疫苗,则他在半年内有99%的可能性得该疾病
C.有1%的把握认为这种疫苗能起到预防该疾病的作用
D.有99%的把握认为这种疫苗能起到预防该疾病的作用
二、能力提升
6.某组织为研究爱好某项运动是否与性别有关进行了一个调查,得到如下列联表,若这两个变量没有关系,则a的可能值为( )
男性 女性 总计
爱好 100 a
不爱好 120 600 720
总计 220
A.720 B.500 C.300 D.200
7.对于分类变量X与Y的统计量,下列说法正确的是( )
A.越大,“X与Y有关系”的可信程度越小
B.越小,“X与Y有关系”的可信程度越小
C.越接近于0,“X与Y没有关系”的可信程度越小
D.越大,“X与Y没有关系”的可信程度越大
8. (多选)某校对“学生性别和喜欢锻炼是否有关”作了一次调查,其中被调查的男女生人数相同,男生喜欢锻炼的人数占男生总人数的,女生喜欢锻炼的人数占女生总人数的.若至少有95%的把握认为“学生性别和喜欢锻炼有关”,则被调查学生中男生的人数可能为( )
附:
0.050 0.010
3.841 6.635
A.35 B.40 C.45 D.50
9. (多选)有关独立性检验的四个命题,其中正确的是( )
A.两个变量的2×2列联表中,对角线上数据的乘积相差越大,说明两个变量有关系的可能性就越大
B.对分类变量X与Y的随机变量来说,越小,“X与Y有关系”的可信程度越小
C.从独立性检验可知:有95%的把握认为秃顶与患心脏病有关,我们说某人秃顶,那么他有95%的可能患有心脏病
D.从独立性检验可知:有99%的把握认为吸烟与患肺癌有关,是指在犯错误的概率不超过1%的前提下,认为吸烟与患肺癌有关
10. (多选)下列四个命题不正确的是( )
A.由独立性检验可知,有9%的把握认为物理成绩与数学成绩有关,若某人数学成绩优秀,则他的物理成绩一定优秀
B.两个随机变量相关性越强,则相关系数的绝对值越接近于0
C.在线性回归方程中,当变量每增加1个单位时,变量增加0.2个单位
D.线性回归直线至少经过其样本数据点中的一个点
11.2020年世界各地相继出现新冠疫情,这已经成为全球性的公共卫生问题.为了测试某种新冠疫苗的效果,某实验室随机抽取100只健康小鼠进行试验,得到如下列联表:
感染 未感染 总计
注射 10 40 50
未注射 20 30 50
总计 30 70 100
则在犯错误的概率不超过______________的前提下,可认为“注射疫苗”与“感染新冠肺炎”有关系.
附:,其中.
0.1 0.05 0.01 0.005 0.001
2.706 3.841 6.635 7.879 10.828
12.现在微信支付被越来越多的人所接受,现从某市市民中随机抽取300人,对是否使用微信支付进行调查,得到下面列联表:
年轻人 非年轻人 总计
经常使用微信支付 165 225
不常使用微信支付
合计 90 300
根据表中数据,我们得到结论:有__________的把握认为使用微信支付与年龄有关.
13.某学校为了制订治理学校门口上学、放学期间家长接送孩子乱停车现象的措施,对全校学生家长进行了问卷调查.根据从中随机抽取的50份调查问卷,得到了如下的列联表:
同意限定区域停车 不同意限定区域停车 合计
男 20 5 25
女 10 15 25
合计 60 20 50
则认为“是否同意限定区域停车与家长的性别有关”的把握约为______________.
14.信息时代人们对通信功能的要求越来越高,5G的拓展运营在西部得到某科技公司的大力推进.已知该公司现有1000名员工,其中女员工400名.为了解员工在某个月内推进5G运行指标的情况,采用分层抽样的方法随机抽取100名员工进行调查,得到如下统计表:
运行指标
频率 0.15 m 0.25 0.15 0.10
(1)求m的值,并估计该科技公司该月推进5G运行指标的平均数(同一组中的数据用该组区间的中点值为代表);
(2)若将推进5G运行指标不低于75的员工评为“璀璨之星”,已知该月被评为“璀璨之星”的男员工有10人,完成如下2×2列联表,并且判断是否有97.5%的把握认为被评为“璀璨之星”与性别有关.
“璀璨之星” 非“璀璨之星” 合计
男员工
女员工
合计
附:.
0.150 0.100 0.050 0.025 0.010
k 2.072 2.706 3.841 5.024 6.635
15.某食品专卖店为调查某种零售食品的受欢迎程度,通过电话回访的形式,随机调查了200名年龄在岁的顾客.以28岁为分界线,按喜欢不喜欢,得到下表,且年龄在岁间不喜欢该食品的频率是.
喜欢 不喜欢 合计
年龄岁(含28岁) 80 m
年龄岁(含40岁) n 40
合计
(I)求表中m,n的值;
(Ⅱ)能否有的把握认为顾客是否喜欢该食品与年龄有关?
附:,其中.
0.050 0.010 0.001
k 3.841 6.635 10.828
答案以及解析
1.答案:C
解析:由题意,,因此有99%以上的把握认为“喜欢篮球与性别有关”.
故选:C.
2.答案:C
解析:由列联表中的数据可得,因此,有的把握认为该市居民是否关注冰雪运动与性别有关.故选:C.
3.答案:B
解析:有90%的把握认为X与Y有关系,,,将选项代入检验,得符合题意.
4.答案:C
解析:由题意,可得,所以有99%的把握认为“是否愿意被外派与年龄有关”,故选C.
5.答案:D
解析:由,可知D正确.
6.答案:B
解析:结合选项,知当时,,所以这两个变量没有关系,故选B.
7.答案:B
解析:根据统计量的意义,知只有B正确.
8.答案:CD
解析:解:由题意被调查的男女生人数相同,设男生的人数为:5n,,由题意可列出列联表:
男生 女生 合计
喜欢锻炼 4n 3n 7n
不喜欢锻炼 n 2n 3n
合计 5n 5n 10n
.
由于有95%的把握认为“学生性别和喜欢锻炼有关”,所以;
解得:,则n的可能取值为:9、10、11、12、13;
则选项中被调查学生中男生的人数可能45或50.
故选:CD.
9.答案:ABD
解析:两个变量的2×2列联表中,对角线上数据的乘积相差越大,则越大,两个变量有关系的可能性越大,所以选项A正确;根据越小,则“X与Y有关系”的可信度越小,所以选项B正确;从独立性检验可知,有95%的把握认为秃顶与患心脏病有关,不表示某人秃顶他有95%的可能患有心脏病,所以选项C不正确;从独立性检验可知,有99%的把握认为吸烟与患肺癌有关,是指在犯错误的概率不超过1%的前提下,认为吸烟与患肺癌有关,是独立性检验的解释,所以选项D正确.故选ABD.
10.答案:ABD
解析:由独立性检验可知,他的物理成绩不一定优秀,故A命题不正确;两个随机变量相关性越强,则相关系数的绝对值越接近于1,故B命题不正确;线性回归直线可能不经过其样本数据点中的任何点,故D命题不正确;易知C命题正确.故选ABD.
11.答案:0.05
解析:由题意得,所以在犯错误的概率不超过0.05的前提下,可认为“注射疫苗”与“感染新冠肺炎”有关系.
12.答案:95%
解析:由条件可得列联表:
年轻人 非年轻人 总计
经常使用微信支付 165 60 225
不常使用微信支付 45 30 75
合计 210 90 300
有95%的把握认为使用微信支付与年龄有关.
13.答案:99.5%
解析:因为,又,所以我们有99.5%的把握认为“是否同意限定区域停车与家长的性别有关”.
14.答案:(1),平均数约为67.
(2)有97.5%的把握认为被评为“璀璨之星”与性别有关.
解析:(1)根据题意,,解得,
平均数.
所以该科技公司该月推进5G运行指标的平均数约为67.
(2)根据题意,利用分层抽样法可知所抽取的100人中男员工60人,女员工40人,被评为“璀璨之星”的有(人),则被评为“璀璨之星”的女员工有(人),
则2×2列联表如下:
“璀璨之星” 非“璀璨之星” 合计
男员工 10 50 60
女员工 15 25 40
合计 25 75 100
则.
所以有97.5%的把握认为被评为“璀璨之星”与性别有关.
15.答案:(1),(2)有
解析:(1)由题中表格中数据可得
,解得,
且,解得.
(2)由(1)可补充列联表为
喜欢 不喜欢 合计
年龄岁(含28岁) 80 20 100
年龄岁(含40岁) 60 40 100
合计 140 60 200
则,
所以有的把握认为顾客是否喜欢该食品与年龄有关.
