八年级 第12讲 等腰三角形的性质[上学期]
文档属性
| 名称 | 八年级 第12讲 等腰三角形的性质[上学期] |
|
|
| 格式 | rar | ||
| 文件大小 | 240.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-03-23 18:29:00 | ||
图片预览


文档简介
等腰三角形的性质
事业常成于坚忍,毁于急躁,我在沙漠中曾亲眼看见,匆忙的旅人落在从容者的后边,疾驰的骏马落在后头,缓步的骆驼继续向前。
―――萨迪:《蔷薇园》
知识纵横
若按边(角)是否相等分类,两边(角)相等的三角形是等腰三角形(isoscelestriangle).等腰三角形是一类特殊三角形,它的两底角相等;等腰三角形是轴对称图形,底边上的高、中线、顶角的平分线互相重合(简称三线合一),特别地,等边三角形(equilateraltriangle)的各边相等,各角都为60度.
解与等腰三角形相关的问题,全等三角形依然是重要的工具,但更多的是思考运用等腰三角形的特殊性质,这些性质为角度的计算、线段相等的证明、直线位置关系的证明等问题提供了新的理论依据,因此,重视全等三角形的运用,又不囿于全等三角形,善于运用等腰三角形的性质探求新的解题途径.
例题求解
【例l】 如图,AOB是一钢架,且∠AOB=100,为使钢架更加坚固,需在其内部添加一些钢管EF、FG、GH……添加的钢管长度都与OE相等,则最多能添加这样的钢管 _______根.
(山东省聊城市中考题)
思路点拨通过角度的计算,确定添加钢管数的最大值.
【例2】如图,若AB=AC,BG=BH,AK=KG,则∠BAC的度数为( ).
A.30。 B.32。 C.36。D.40。
(武汉市选拔赛试题)
思路点拨 图中有很多相关的角,用∠BAC的代数式表示这些角,建立关于∠BAC的方程.
【例3】如图,在△ABC中,已知∠A=900,AB=AC,D为AC上一点,AE⊥BD于E,延长AE交BC于F.问:当点D满足什么条件时,∠ADB=∠CDF请说明理由.
(安徽省竞赛题改编题)
思路点拨本例是探索条件的问题,可先假定结论成立,逐步逆推过去,找到相应的条件,若∠ADB=∠CDF,这一结论如何用 因∠ADB与∠CDF对应的三角形不全等,故需构造全等三角形,而作顶角的平分线或底边上的高(中线)是等腰三角形中一条常用辅助线.
【例4】如图,在△ABC中,AC=BC,∠ACB=900,D是AC上一点,AE⊥BD交BD的延长线于E,且AE=BD.求证:BD是∠ABC的角平分线.
(北京市竞赛题)
思路点拨AE边上的高与LABC的平分线重合,联想到等腰三角形,通过作辅助线构造全等三角形、等腰三角形.
【例5】 如图,在△ABC中,∠BAC=∠BCA= 440,M为△ABC内一点,使得∠MCA=300,∠MAC=160.求∠BMC的度数.
(2005年北京市竞赛题)。
思路点拨:作等腰△ABC的对称轴,通过计算,证明全等三角形.
基础夯实:
1.如图,△ABC中,已知AB=AC,要使AD=AE,需要添加的一个条件是_____.
(济南市中考题)
2.等腰三角形一腰上的中线把这个三角形的周长分成12cm和 21cm两部分,则这个等腰三角形底边的长为______.
3.一个等腰三角形的一条高等于腰长的一半,则这个等腰三角形的底角的度数为_____
(2005年河北省竞赛题)
4.如图,△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,若BF=AC,则∠ABC的大小是________ .
(烟台市中考题)
5.△ABC的一个内角的大小是40。,且∠A=∠B,那么∠C的外角的大小是( ).
A.1400 B.800或1000 C.1000或1400 D.800或1400
6.已知△ABC中,AB=AC,∠BAC=900,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③;④EF=AP.当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),上述结论中始终正确的是 ( ).
A.1个 B.2个 C.3个D.4个
(苏州市中考题)
7.如图,在△ABC中,∠ACB=900,AC=AE,BC=BF,则∠ECF=( ).
A.600 B.450 C.300 D.不确定
8.如图,在等边△ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数是( ).
A.450 B.550 C.600 D.750
(菏泽市中考题)
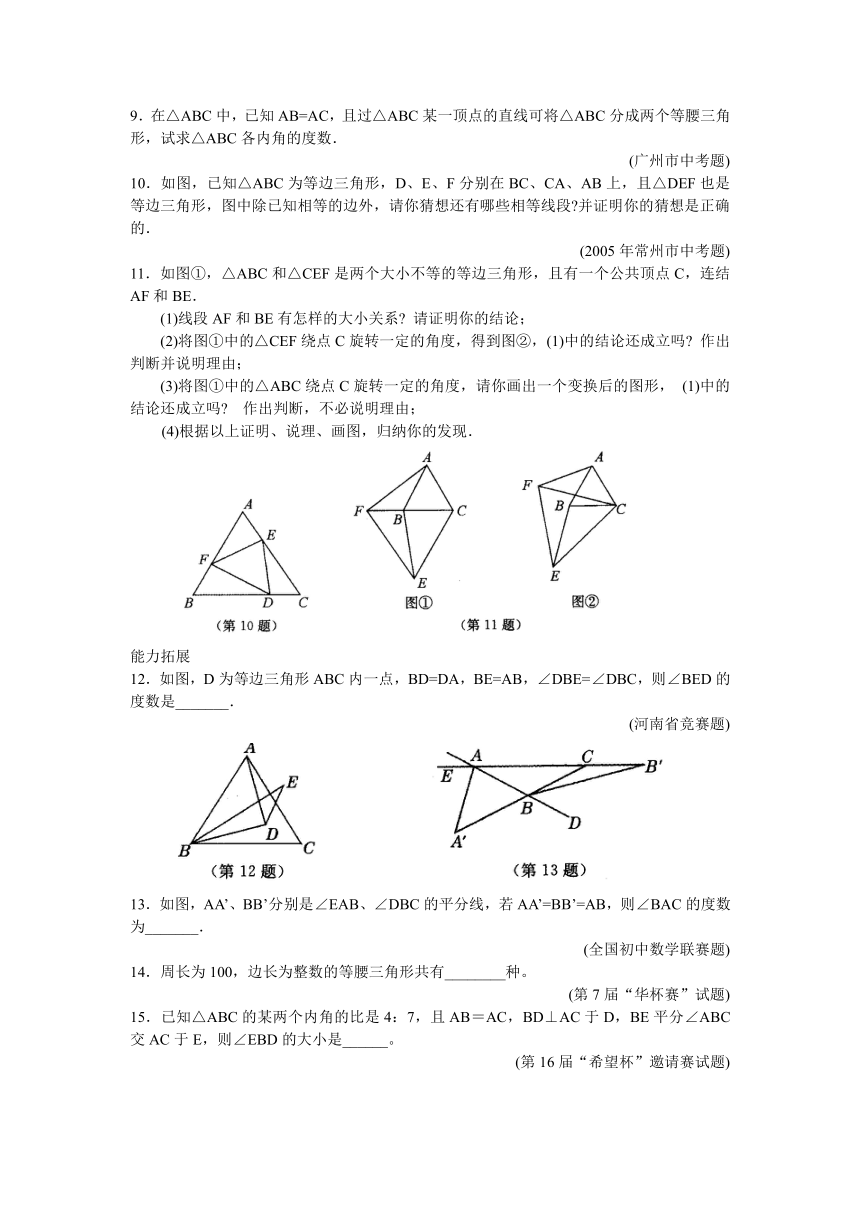
9.在△ABC中,已知AB=AC,且过△ABC某一顶点的直线可将△ABC分成两个等腰三角形,试求△ABC各内角的度数.
(广州市中考题)
10.如图,已知△ABC为等边三角形,D、E、F分别在BC、CA、AB上,且△DEF也是等边三角形,图中除已知相等的边外,请你猜想还有哪些相等线段 并证明你的猜想是正确的.
(2005年常州市中考题)
11.如图①,△ABC和△CEF是两个大小不等的等边三角形,且有一个公共顶点C,连结AF和BE.
(1)线段AF和BE有怎样的大小关系 请证明你的结论;
(2)将图①中的△CEF绕点C旋转一定的角度,得到图②,(1)中的结论还成立吗 作出判断并说明理由;
(3)将图①中的△ABC绕点C旋转一定的角度,请你画出一个变换后的图形, (1)中的结论还成立吗 作出判断,不必说明理由;
(4)根据以上证明、说理、画图,归纳你的发现.
能力拓展
12.如图,D为等边三角形ABC内一点,BD=DA,BE=AB,∠DBE=∠DBC,则∠BED的度数是_______.
(河南省竞赛题)
13.如图,AA’、BB’分别是∠EAB、∠DBC的平分线,若AA’=BB’=AB,则∠BAC的度数为_______.
(全国初中数学联赛题)
14.周长为100,边长为整数的等腰三角形共有________种。
(第7届“华杯赛”试题)
15.已知△ABC的某两个内角的比是4:7,且AB=AC,BD⊥AC于D,BE平分∠ABC交AC于E,则∠EBD的大小是______。
(第16届“希望杯”邀请赛试题)
16.如图,△ABC中,∠BAC=1200, AD⊥BC于D,且AB+BD=DC,则∠C的大小是( ).
A.200 B.250 C.300 D.450
17.如图,在等腰直角△ABC中,AD为斜边上的高,以D为端点任作两条互相垂直的射线与两腰相交于E、F,连结EF与AD相交于G,则∠AED与∠AGF的关系为( ).
A.∠AED>∠AGF B.∠AED=∠AGF
C.∠AED<∠AGF D.不能确定
(《学习报》公开赛试题)
18.如图,△ABC中,∠ACB=900, ∠A=200,将△ABC绕点C按逆时针方向旋转α角到△A’B’C’的位置,B在A’B’上,CA’交AB于D,则∠BDC的度数为 ( ).
A.400 B.450 C.500 D.600
(2004年山东省竞赛题)
19.如图,已知AC平分∠DAB,CE⊥AB于E,AB=AD+2BE,则下列结论:①AE=(AB+AD);②∠DAB+∠DCB=1800;③CD=CB ④.其中正确结论的个数是( )。
A.1个 B.2个 C.3个 D.4个
20.如图,已知△ABC是等边三角形,D、E分别在BA、BC的延长线上,且AD=BE.求证:DC=DE.
(第20题) (第21题)
21.如图,AE、AD是直线且AB=BC=CD=DE=EF=FG=GA,若∠DAE=α0求α的值.
(第20届香港中学生数学竞赛题)
22.如图,△ABC中,AB=AC,∠BAC=800,O为△ABC内一点,且∠OBC=100,∠OCA=200,求∠BAO的度数.
(天津市竞赛题)
综合创新:
23.如图,△ABC是边长为1的等边三角形,△BDC是顶角△BDC=1200的等腰三角形,以D为顶点作一个60度角,角的两边分别交AB于M,交AC于N连结MN,形成一个三角形.求证:△AMN的周长等于2.
24.如图,在△ABC中,已知∠C=600,AC>BC,又△ABC’、△BCA’、△CAB’都是△ABC形外的等边三角形,而点D在AC上,且BC=DC.
(1)证明:△C’BD≌△B’DC;
(2)证明:△AC’D≌△DB’A;
(3)对△ABC、△ABC’、△BCA’、△CAB’,从面积大小关系上,你能得出什么结论
(第17届江苏省竞赛题)
事业常成于坚忍,毁于急躁,我在沙漠中曾亲眼看见,匆忙的旅人落在从容者的后边,疾驰的骏马落在后头,缓步的骆驼继续向前。
―――萨迪:《蔷薇园》
知识纵横
若按边(角)是否相等分类,两边(角)相等的三角形是等腰三角形(isoscelestriangle).等腰三角形是一类特殊三角形,它的两底角相等;等腰三角形是轴对称图形,底边上的高、中线、顶角的平分线互相重合(简称三线合一),特别地,等边三角形(equilateraltriangle)的各边相等,各角都为60度.
解与等腰三角形相关的问题,全等三角形依然是重要的工具,但更多的是思考运用等腰三角形的特殊性质,这些性质为角度的计算、线段相等的证明、直线位置关系的证明等问题提供了新的理论依据,因此,重视全等三角形的运用,又不囿于全等三角形,善于运用等腰三角形的性质探求新的解题途径.
例题求解
【例l】 如图,AOB是一钢架,且∠AOB=100,为使钢架更加坚固,需在其内部添加一些钢管EF、FG、GH……添加的钢管长度都与OE相等,则最多能添加这样的钢管 _______根.
(山东省聊城市中考题)
思路点拨通过角度的计算,确定添加钢管数的最大值.
【例2】如图,若AB=AC,BG=BH,AK=KG,则∠BAC的度数为( ).
A.30。 B.32。 C.36。D.40。
(武汉市选拔赛试题)
思路点拨 图中有很多相关的角,用∠BAC的代数式表示这些角,建立关于∠BAC的方程.
【例3】如图,在△ABC中,已知∠A=900,AB=AC,D为AC上一点,AE⊥BD于E,延长AE交BC于F.问:当点D满足什么条件时,∠ADB=∠CDF请说明理由.
(安徽省竞赛题改编题)
思路点拨本例是探索条件的问题,可先假定结论成立,逐步逆推过去,找到相应的条件,若∠ADB=∠CDF,这一结论如何用 因∠ADB与∠CDF对应的三角形不全等,故需构造全等三角形,而作顶角的平分线或底边上的高(中线)是等腰三角形中一条常用辅助线.
【例4】如图,在△ABC中,AC=BC,∠ACB=900,D是AC上一点,AE⊥BD交BD的延长线于E,且AE=BD.求证:BD是∠ABC的角平分线.
(北京市竞赛题)
思路点拨AE边上的高与LABC的平分线重合,联想到等腰三角形,通过作辅助线构造全等三角形、等腰三角形.
【例5】 如图,在△ABC中,∠BAC=∠BCA= 440,M为△ABC内一点,使得∠MCA=300,∠MAC=160.求∠BMC的度数.
(2005年北京市竞赛题)。
思路点拨:作等腰△ABC的对称轴,通过计算,证明全等三角形.
基础夯实:
1.如图,△ABC中,已知AB=AC,要使AD=AE,需要添加的一个条件是_____.
(济南市中考题)
2.等腰三角形一腰上的中线把这个三角形的周长分成12cm和 21cm两部分,则这个等腰三角形底边的长为______.
3.一个等腰三角形的一条高等于腰长的一半,则这个等腰三角形的底角的度数为_____
(2005年河北省竞赛题)
4.如图,△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,若BF=AC,则∠ABC的大小是________ .
(烟台市中考题)
5.△ABC的一个内角的大小是40。,且∠A=∠B,那么∠C的外角的大小是( ).
A.1400 B.800或1000 C.1000或1400 D.800或1400
6.已知△ABC中,AB=AC,∠BAC=900,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③;④EF=AP.当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),上述结论中始终正确的是 ( ).
A.1个 B.2个 C.3个D.4个
(苏州市中考题)
7.如图,在△ABC中,∠ACB=900,AC=AE,BC=BF,则∠ECF=( ).
A.600 B.450 C.300 D.不确定
8.如图,在等边△ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数是( ).
A.450 B.550 C.600 D.750
(菏泽市中考题)
9.在△ABC中,已知AB=AC,且过△ABC某一顶点的直线可将△ABC分成两个等腰三角形,试求△ABC各内角的度数.
(广州市中考题)
10.如图,已知△ABC为等边三角形,D、E、F分别在BC、CA、AB上,且△DEF也是等边三角形,图中除已知相等的边外,请你猜想还有哪些相等线段 并证明你的猜想是正确的.
(2005年常州市中考题)
11.如图①,△ABC和△CEF是两个大小不等的等边三角形,且有一个公共顶点C,连结AF和BE.
(1)线段AF和BE有怎样的大小关系 请证明你的结论;
(2)将图①中的△CEF绕点C旋转一定的角度,得到图②,(1)中的结论还成立吗 作出判断并说明理由;
(3)将图①中的△ABC绕点C旋转一定的角度,请你画出一个变换后的图形, (1)中的结论还成立吗 作出判断,不必说明理由;
(4)根据以上证明、说理、画图,归纳你的发现.
能力拓展
12.如图,D为等边三角形ABC内一点,BD=DA,BE=AB,∠DBE=∠DBC,则∠BED的度数是_______.
(河南省竞赛题)
13.如图,AA’、BB’分别是∠EAB、∠DBC的平分线,若AA’=BB’=AB,则∠BAC的度数为_______.
(全国初中数学联赛题)
14.周长为100,边长为整数的等腰三角形共有________种。
(第7届“华杯赛”试题)
15.已知△ABC的某两个内角的比是4:7,且AB=AC,BD⊥AC于D,BE平分∠ABC交AC于E,则∠EBD的大小是______。
(第16届“希望杯”邀请赛试题)
16.如图,△ABC中,∠BAC=1200, AD⊥BC于D,且AB+BD=DC,则∠C的大小是( ).
A.200 B.250 C.300 D.450
17.如图,在等腰直角△ABC中,AD为斜边上的高,以D为端点任作两条互相垂直的射线与两腰相交于E、F,连结EF与AD相交于G,则∠AED与∠AGF的关系为( ).
A.∠AED>∠AGF B.∠AED=∠AGF
C.∠AED<∠AGF D.不能确定
(《学习报》公开赛试题)
18.如图,△ABC中,∠ACB=900, ∠A=200,将△ABC绕点C按逆时针方向旋转α角到△A’B’C’的位置,B在A’B’上,CA’交AB于D,则∠BDC的度数为 ( ).
A.400 B.450 C.500 D.600
(2004年山东省竞赛题)
19.如图,已知AC平分∠DAB,CE⊥AB于E,AB=AD+2BE,则下列结论:①AE=(AB+AD);②∠DAB+∠DCB=1800;③CD=CB ④.其中正确结论的个数是( )。
A.1个 B.2个 C.3个 D.4个
20.如图,已知△ABC是等边三角形,D、E分别在BA、BC的延长线上,且AD=BE.求证:DC=DE.
(第20题) (第21题)
21.如图,AE、AD是直线且AB=BC=CD=DE=EF=FG=GA,若∠DAE=α0求α的值.
(第20届香港中学生数学竞赛题)
22.如图,△ABC中,AB=AC,∠BAC=800,O为△ABC内一点,且∠OBC=100,∠OCA=200,求∠BAO的度数.
(天津市竞赛题)
综合创新:
23.如图,△ABC是边长为1的等边三角形,△BDC是顶角△BDC=1200的等腰三角形,以D为顶点作一个60度角,角的两边分别交AB于M,交AC于N连结MN,形成一个三角形.求证:△AMN的周长等于2.
24.如图,在△ABC中,已知∠C=600,AC>BC,又△ABC’、△BCA’、△CAB’都是△ABC形外的等边三角形,而点D在AC上,且BC=DC.
(1)证明:△C’BD≌△B’DC;
(2)证明:△AC’D≌△DB’A;
(3)对△ABC、△ABC’、△BCA’、△CAB’,从面积大小关系上,你能得出什么结论
(第17届江苏省竞赛题)
