4.3 解直角三角形(精讲课件)(共12张PPT)
文档属性
| 名称 | 4.3 解直角三角形(精讲课件)(共12张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 646.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-21 20:59:15 | ||
图片预览




文档简介
(共12张PPT)
4.3 解直角三角形
湘教版数学九年级上册
在直角三角形中除直角外,一共有5个元素,即3条边和2个锐角,已知哪些元素能求出其他的元素呢?
情境导入
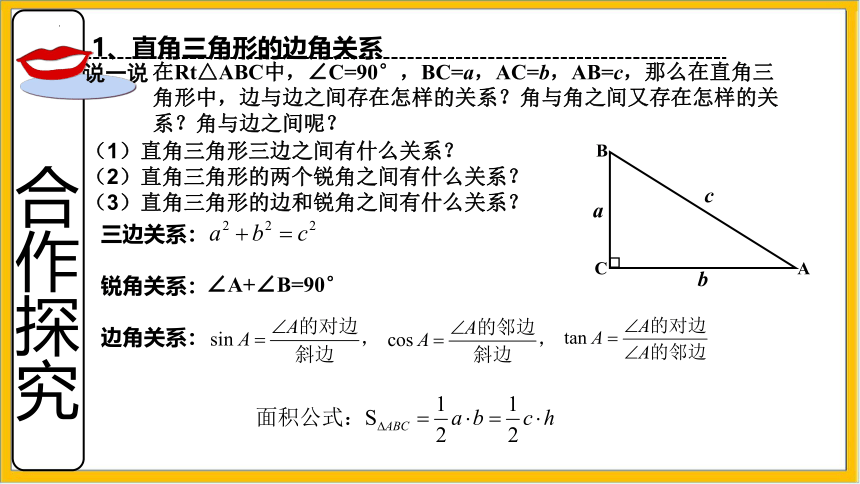
在Rt△ABC中,∠C=90°,BC=a,AC=b,AB=c,那么在直角三角形中,边与边之间存在怎样的关系?角与角之间又存在怎样的关系?角与边之间呢?
三边关系:
锐角关系:
边角关系:
A
B
C
a
b
c
∠A+∠B=90°
说一说
(1)直角三角形三边之间有什么关系?
(2)直角三角形的两个锐角之间有什么关系?
(3)直角三角形的边和锐角之间有什么关系?
1、直角三角形的边角关系
合作探究
2、解直角三角形的定义
根据下列每一组条件,能画出多少个直角三角形(全等的直角三角形算一个)?
(1)一个锐角为40°;
(2)一个锐角为40°,它的邻边长为3cm;
(3)一个锐角为40°,它的对边长为3cm;
(4)一个锐角为40°,斜边长为3cm;
(5)一个锐角为40°,一条直角边长为3cm。
做一做
以上这些问题的结论存在什么规律?这个结论正确吗?
说一说
归纳
在直角三角形中,除直角外的5个元素(3条边和2个锐角),只要知道其中的2个元素(至少有一个是边),利用上述关系式,就可以求出其余的3个未知元素,这叫作解直角三角形。
[议一议]为什么两个元素中必有一条边?在直角三角形中,若知道的2个元素都是直角,能求出直角三角形的边吗?
合作探究
例1 如图,在Rt△ABC中,∠C=90°,∠A=30°,a=5,求∠B,b,c。
举
例
解:在Rt△ABC中,∠C=90°,∠A=30°,
∴∠B=90°-∠A=60°,
∵a=5
典例解析
举
例
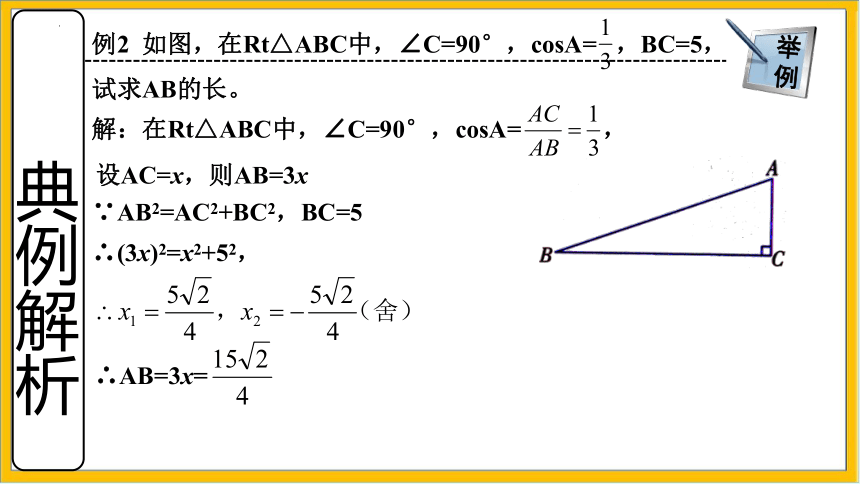
例2 如图,在Rt△ABC中,∠C=90°,cosA= ,BC=5,试求AB的长。
解:在Rt△ABC中,∠C=90°,cosA= ,
设AC=x,则AB=3x
∵AB2=AC2+BC2,BC=5
∴(3x)2=x2+52,
∴AB=3x=
典例解析
2.如图,在△ABC中,∠A=30°,∠B=45°,AC=10cm,求AB的长.
1.在△ABC中,AD是BC边上的高,∠C=45°,sinB= ,AD=1.求BC的长.
D
课堂练习
3.在△ABC中,∠C=90°,AC=16,sinB=0.8,则BC的长是( )A.12 B.16 C.20 D.24
4.△ABC中,AB=12,AC= ,∠B=30°,则△ABC的面积是 .
C
B
A
16
A
12
12
30°
30°
6
6
课堂练习
3.在△ABC中,∠C=90°,AC=16,sinB=0.8,则BC的长是( )A.12 B.16 C.20 D.24
4.△ABC中,AB=12,AC= ,∠B=30°,则△ABC的面积是 .
5.在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c.根据下列条件解直角三角形.
(1)已知a=5,∠B=60°;
(2)已知a= ,b= .
A
课堂练习
课堂小结
通过本节课的学习,你有什么收获与体会?
作业设计
1. 在Rt△ABC中,∠C=90°,∠B=45°,b=3cm,BC=5,求a,c的长度.
2. 在Rt△ABC中,∠C=90°,a=6cm,c=10cm,求b,∠A,∠B(角度精
确到1°).
3. 在Rt△ABC中,∠C=90°,∠A=30°,c=16cm,求a,b的长度.
再 见
4.3 解直角三角形
湘教版数学九年级上册
在直角三角形中除直角外,一共有5个元素,即3条边和2个锐角,已知哪些元素能求出其他的元素呢?
情境导入
在Rt△ABC中,∠C=90°,BC=a,AC=b,AB=c,那么在直角三角形中,边与边之间存在怎样的关系?角与角之间又存在怎样的关系?角与边之间呢?
三边关系:
锐角关系:
边角关系:
A
B
C
a
b
c
∠A+∠B=90°
说一说
(1)直角三角形三边之间有什么关系?
(2)直角三角形的两个锐角之间有什么关系?
(3)直角三角形的边和锐角之间有什么关系?
1、直角三角形的边角关系
合作探究
2、解直角三角形的定义
根据下列每一组条件,能画出多少个直角三角形(全等的直角三角形算一个)?
(1)一个锐角为40°;
(2)一个锐角为40°,它的邻边长为3cm;
(3)一个锐角为40°,它的对边长为3cm;
(4)一个锐角为40°,斜边长为3cm;
(5)一个锐角为40°,一条直角边长为3cm。
做一做
以上这些问题的结论存在什么规律?这个结论正确吗?
说一说
归纳
在直角三角形中,除直角外的5个元素(3条边和2个锐角),只要知道其中的2个元素(至少有一个是边),利用上述关系式,就可以求出其余的3个未知元素,这叫作解直角三角形。
[议一议]为什么两个元素中必有一条边?在直角三角形中,若知道的2个元素都是直角,能求出直角三角形的边吗?
合作探究
例1 如图,在Rt△ABC中,∠C=90°,∠A=30°,a=5,求∠B,b,c。
举
例
解:在Rt△ABC中,∠C=90°,∠A=30°,
∴∠B=90°-∠A=60°,
∵a=5
典例解析
举
例
例2 如图,在Rt△ABC中,∠C=90°,cosA= ,BC=5,试求AB的长。
解:在Rt△ABC中,∠C=90°,cosA= ,
设AC=x,则AB=3x
∵AB2=AC2+BC2,BC=5
∴(3x)2=x2+52,
∴AB=3x=
典例解析
2.如图,在△ABC中,∠A=30°,∠B=45°,AC=10cm,求AB的长.
1.在△ABC中,AD是BC边上的高,∠C=45°,sinB= ,AD=1.求BC的长.
D
课堂练习
3.在△ABC中,∠C=90°,AC=16,sinB=0.8,则BC的长是( )A.12 B.16 C.20 D.24
4.△ABC中,AB=12,AC= ,∠B=30°,则△ABC的面积是 .
C
B
A
16
A
12
12
30°
30°
6
6
课堂练习
3.在△ABC中,∠C=90°,AC=16,sinB=0.8,则BC的长是( )A.12 B.16 C.20 D.24
4.△ABC中,AB=12,AC= ,∠B=30°,则△ABC的面积是 .
5.在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c.根据下列条件解直角三角形.
(1)已知a=5,∠B=60°;
(2)已知a= ,b= .
A
课堂练习
课堂小结
通过本节课的学习,你有什么收获与体会?
作业设计
1. 在Rt△ABC中,∠C=90°,∠B=45°,b=3cm,BC=5,求a,c的长度.
2. 在Rt△ABC中,∠C=90°,a=6cm,c=10cm,求b,∠A,∠B(角度精
确到1°).
3. 在Rt△ABC中,∠C=90°,∠A=30°,c=16cm,求a,b的长度.
再 见
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
