4.1.2 余弦 (精讲课件)(共13张PPT)
文档属性
| 名称 | 4.1.2 余弦 (精讲课件)(共13张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 559.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-22 17:00:33 | ||
图片预览




文档简介
(共13张PPT)
4.1.2 余弦
湘教版数学九年级上册
上节课我们发现:只要直角三角形的锐角固定,它的对边与斜边的比值也固定。
设问:直角三角形的锐角固定,它的邻边与斜边的比值是否也固定呢?
复习导入
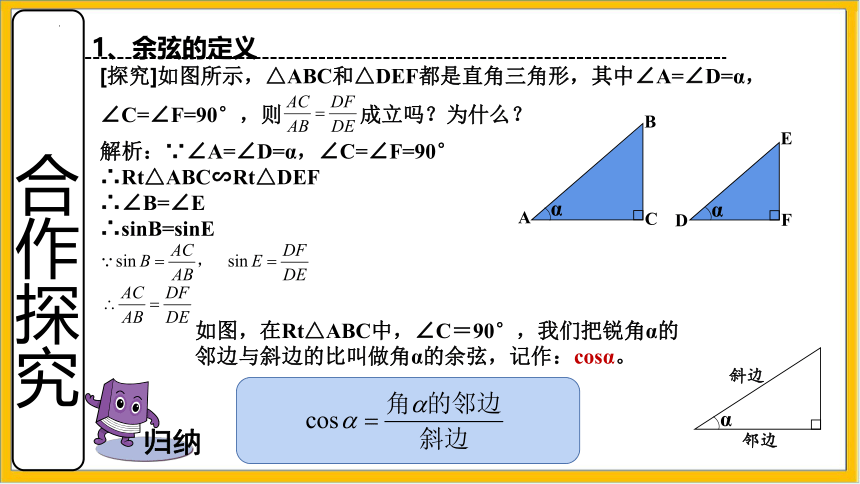
1、余弦的定义
B
A
C
α
E
D
F
α
解析:∵∠A=∠D=α,∠C=∠F=90°
∴Rt△ABC∽Rt△DEF
∴∠B=∠E
∴sinB=sinE
归纳
如图,在Rt△ABC中,∠C=90°,我们把锐角α的邻边与斜边的比叫做角α的余弦,记作:cosα。
α
斜边
邻边
[探究]如图所示,△ABC和△DEF都是直角三角形,其中∠A=∠D=α,∠C=∠F=90°,则 成立吗?为什么?
合作探究
练习
如图,在Rt△ABC中,∠C=90°,AC=5,AB=13,则:sinA= ,sinB= ,cosA= ,cosB= 。
A
C
B
5
12
13
课堂练习
2、互余两锐角的正弦值与余弦值的关系
[讨论交流]在学习了锐角的正弦函数和余弦函数之后,这两个函数之间存在着怎样的关系呢?
A
B
C
a
b
c
如图,在Rt△ABC中,∠C=90°,∠A=α
∵∠A=α,
∴∠B= 90°-α。
∵sinA =sinα= ,cosB= 。
∴sinA=cosB
∴sinα=cos(90°-α)
归纳
互余
关系
任意锐角的余弦值等于它的余角的正弦值,任意锐角的正弦值等于它的余角的余弦值。
合作探究
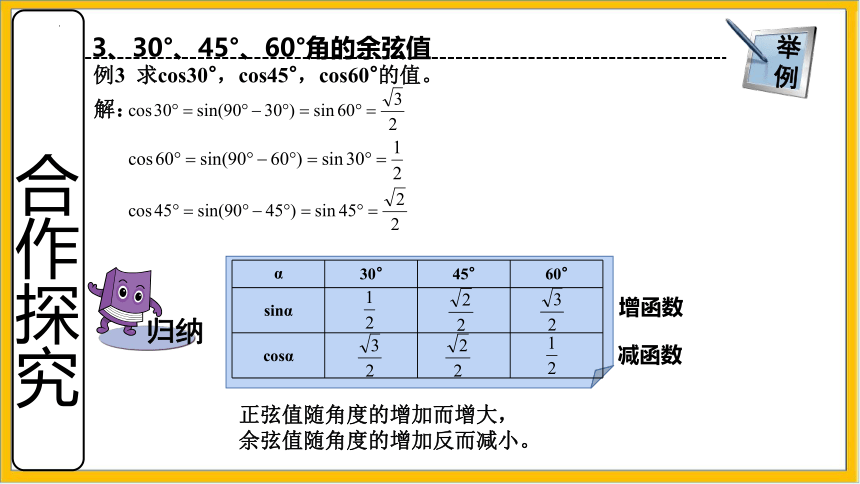
3、30°、45°、60°角的余弦值
例3 求cos30°,cos45°,cos60°的值。
解:
正弦值随角度的增加而增大,
余弦值随角度的增加反而减小。
举
例
归纳
α 30° 45° 60°
sinα
cosα
增函数
减函数
合作探究
举
例
解:原式=
4、余弦的计算
例4 计算:
典例解析
1.如图所示,已知∠A为锐角,∠C=90°sinA= ,求cosA,sinB,cosB的值.
2.已知在Rt△ABC中,∠C=90°,∠A=α,AC=2,那么AB的长等于( )
A. B. C. D.
C
课堂练习
3.△ABC中,∠A,∠B都是锐角,且sinA= ,cosB= ,则△ABC的形状是( )
A.直角三角形 B.钝角三角形
C.锐角三角形 D.锐角三角形或钝角三角形
C
4.如图,点A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( )
A. B. C. D.
5.△ABC中,若AC= ,BC= ,AB=3,则cosA= .
C
课堂练习
6.如图,在△ABC中,AB=AC,BD⊥AC于点D.AC=10,cosA= ,求BC的长.
课堂练习
课堂小结
通过本节课的学习,你有什么收获与体会?
作业设计
1. 如图,在Rt△ABC中,∠C=90°,AC=5,AB=7.求cosA,cosB的值.
2. 计算:
(1)cos260°-sin245°; (2)1-2cos30°cos45°.
再 见
4.1.2 余弦
湘教版数学九年级上册
上节课我们发现:只要直角三角形的锐角固定,它的对边与斜边的比值也固定。
设问:直角三角形的锐角固定,它的邻边与斜边的比值是否也固定呢?
复习导入
1、余弦的定义
B
A
C
α
E
D
F
α
解析:∵∠A=∠D=α,∠C=∠F=90°
∴Rt△ABC∽Rt△DEF
∴∠B=∠E
∴sinB=sinE
归纳
如图,在Rt△ABC中,∠C=90°,我们把锐角α的邻边与斜边的比叫做角α的余弦,记作:cosα。
α
斜边
邻边
[探究]如图所示,△ABC和△DEF都是直角三角形,其中∠A=∠D=α,∠C=∠F=90°,则 成立吗?为什么?
合作探究
练习
如图,在Rt△ABC中,∠C=90°,AC=5,AB=13,则:sinA= ,sinB= ,cosA= ,cosB= 。
A
C
B
5
12
13
课堂练习
2、互余两锐角的正弦值与余弦值的关系
[讨论交流]在学习了锐角的正弦函数和余弦函数之后,这两个函数之间存在着怎样的关系呢?
A
B
C
a
b
c
如图,在Rt△ABC中,∠C=90°,∠A=α
∵∠A=α,
∴∠B= 90°-α。
∵sinA =sinα= ,cosB= 。
∴sinA=cosB
∴sinα=cos(90°-α)
归纳
互余
关系
任意锐角的余弦值等于它的余角的正弦值,任意锐角的正弦值等于它的余角的余弦值。
合作探究
3、30°、45°、60°角的余弦值
例3 求cos30°,cos45°,cos60°的值。
解:
正弦值随角度的增加而增大,
余弦值随角度的增加反而减小。
举
例
归纳
α 30° 45° 60°
sinα
cosα
增函数
减函数
合作探究
举
例
解:原式=
4、余弦的计算
例4 计算:
典例解析
1.如图所示,已知∠A为锐角,∠C=90°sinA= ,求cosA,sinB,cosB的值.
2.已知在Rt△ABC中,∠C=90°,∠A=α,AC=2,那么AB的长等于( )
A. B. C. D.
C
课堂练习
3.△ABC中,∠A,∠B都是锐角,且sinA= ,cosB= ,则△ABC的形状是( )
A.直角三角形 B.钝角三角形
C.锐角三角形 D.锐角三角形或钝角三角形
C
4.如图,点A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( )
A. B. C. D.
5.△ABC中,若AC= ,BC= ,AB=3,则cosA= .
C
课堂练习
6.如图,在△ABC中,AB=AC,BD⊥AC于点D.AC=10,cosA= ,求BC的长.
课堂练习
课堂小结
通过本节课的学习,你有什么收获与体会?
作业设计
1. 如图,在Rt△ABC中,∠C=90°,AC=5,AB=7.求cosA,cosB的值.
2. 计算:
(1)cos260°-sin245°; (2)1-2cos30°cos45°.
再 见
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
