3.4.2 相似三角形的性质(1)(精讲课件)(共12张PPT)
文档属性
| 名称 | 3.4.2 相似三角形的性质(1)(精讲课件)(共12张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 555.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-22 17:01:36 | ||
图片预览



文档简介
(共12张PPT)
3.4.2 相似三角形的性质(1)
湘教版数学九年级上册
情境导入
说一说
(1)相似三角形的判定方法有哪些?
利用平行证相似;
利用两角证相似;
利用两边夹角证相似;
利用三边证相似。
情境导入
说一说
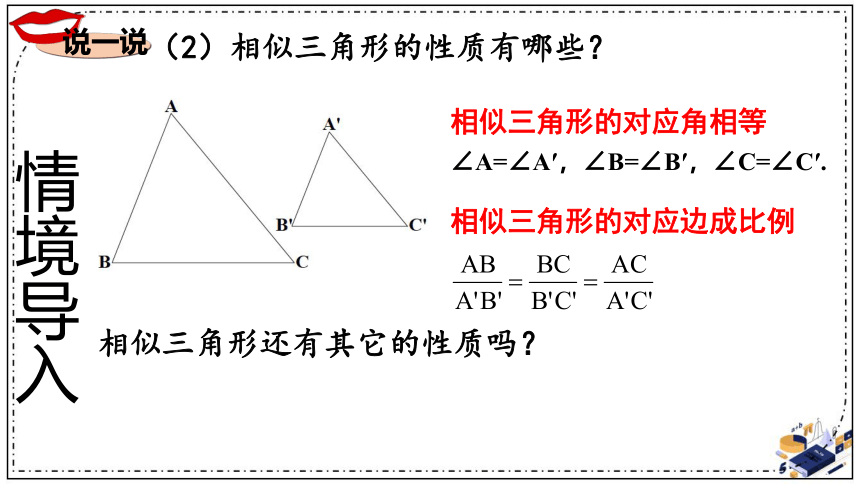
(2)相似三角形的性质有哪些?
相似三角形的对应角相等
相似三角形的对应边成比例
相似三角形还有其它的性质吗?
∠A=∠A′,∠B=∠B′,∠C=∠C′.
合作探究
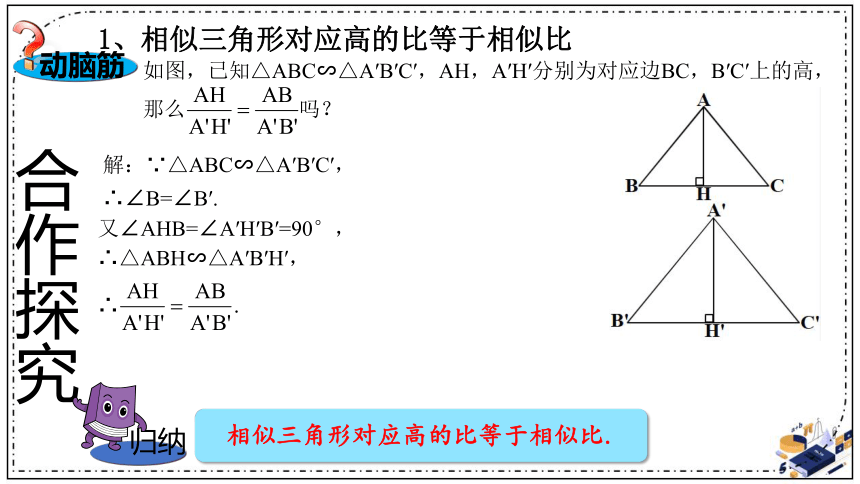
1、相似三角形对应高的比等于相似比
动脑筋
如图,已知△ABC∽△A′B′C′,AH,A′H′分别为对应边BC,B′C′上的高,那么 吗?
解:∵△ABC∽△A′B′C′,
∴∠B=∠B′.
又∠AHB=∠A′H′B′=90°,
∴△ABH∽△A′B′H′,
归纳
相似三角形对应高的比等于相似比.
∴
合作探究
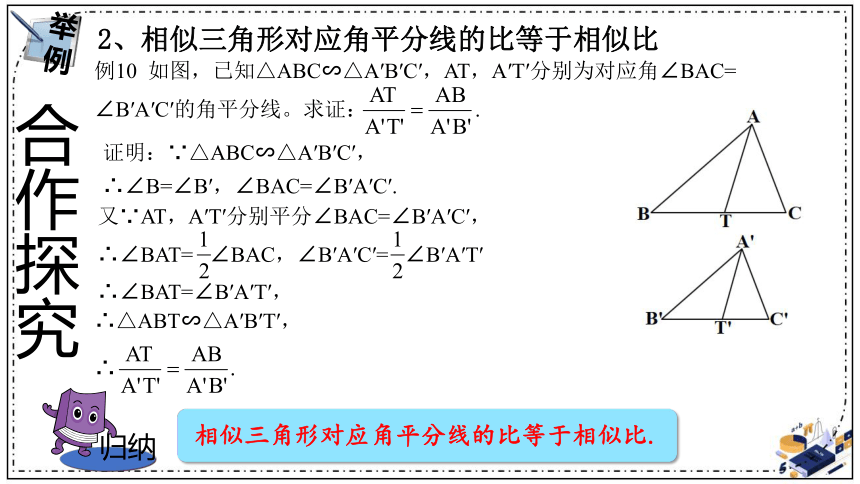
2、相似三角形对应角平分线的比等于相似比
例10 如图,已知△ABC∽△A′B′C′,AT,A′T′分别为对应角∠BAC=
∠B′A′C′的角平分线。求证: .
举
例
证明:∵△ABC∽△A′B′C′,
∴∠B=∠B′,∠BAC=∠B′A′C′.
又∵AT,A′T′分别平分∠BAC=∠B′A′C′,
∴△ABT∽△A′B′T′,
∴
∴∠BAT=∠B′A′T′,
∴∠BAT= ∠BAC,∠B′A′C′= ∠B′A′T′
归纳
相似三角形对应角平分线的比等于相似比.
合作探究
3、相似三角形对应中线的比等于相似比
已知△ABC∽△A′B′C′,若AD,A′D′分别为△ABC,△A′B′C′的中线,则 成立吗?由此你得出什么结论?
证明:∵△ABC∽△A′B′C′,
又AD,A′D′分别平分BC、B′C′,
∴△ABD∽△A′B′D′,
∴
议一议
∴BD= BC,B′D′= B′C′
归纳
相似三角形对应中线的比等于相似比.
∴∠B=∠B′,
∴
合作探究
例9 如图,AB//PQ,AB=100m,PQ=120m。点P,A,C在一条直线上,点Q,B,C也在一条直线上。若AB与PQ的距离是40m,求点C到直线PQ的距离。
解:过点C作CD⊥PQ,交PQ的延长线于D,交AB的延长线于E
∴△CAB∽△CPQ,CE⊥AB,DE=40m.
∵AB=100m,PQ=120m,CE=CD-DE,
∴CD=240m.
∴
举
例
∵AB//PQ,
答:点C到直线PQ的距离为240m.
∴
D
E
课堂练习
练习
1、要制作两个形状相同的三角形框架,其中一个三角形的三边长分别
为5cm,6cm和9cm,另一个三角形的最短边长为2.5cm,则它的最长边
为( )
A. 3cm B. 4cm C. 4.5cm D. 5cm
2、如下左图,四边形ABCD的对角线AC,BD相交于点O,AD//BC,G是BD的中点。若AD=3,BC=9,则GO︰BG等于( )
A. 1︰2 B. 1︰3 C. 2︰3 D. 11︰20
3、如上右图,在△ABC中,DE//BC, ,DE=6,则BC的长是 ;
C
A
18
课堂练习
练习
4、如图所示,某同学拿着一把刻有厘米分划的小尺,站在距旗杆约30m的地方,把手臂向前伸直且让小尺竖直,看到尺上大约有24个分划恰好遮住旗杆。已知此同学的臂长约为60cm,求旗杆的大致高度。
解:由已知得:BC=24cm=0.24m,CM=60cm=0.6m,
EN=30m,BC//DE,CM//EN,
∴△ABC∽△ADE,△ACM∽△AEN
∴DE=12m.
答:旗杆大致高12m.
课堂小结
通过本节课的学习,你有什么收获与体会?
动脑筋
作业设计
练习
1、已知△ABC∽△DEF,AM,DN分别为△ABC,△DEF的一条中线,且AM=6cm,AB=8cm,DE=4cm,求DN的长.
2、如图,△ABC∽△A′B′C′,AD,BE分别是△ABC的高和中线,A′D′,B′E′分别是△A′B′C′的高和中线,且AD=4,A′D′=3,BE=6,求B′E′的长.
DN=3cm
再 见
3.4.2 相似三角形的性质(1)
湘教版数学九年级上册
情境导入
说一说
(1)相似三角形的判定方法有哪些?
利用平行证相似;
利用两角证相似;
利用两边夹角证相似;
利用三边证相似。
情境导入
说一说
(2)相似三角形的性质有哪些?
相似三角形的对应角相等
相似三角形的对应边成比例
相似三角形还有其它的性质吗?
∠A=∠A′,∠B=∠B′,∠C=∠C′.
合作探究
1、相似三角形对应高的比等于相似比
动脑筋
如图,已知△ABC∽△A′B′C′,AH,A′H′分别为对应边BC,B′C′上的高,那么 吗?
解:∵△ABC∽△A′B′C′,
∴∠B=∠B′.
又∠AHB=∠A′H′B′=90°,
∴△ABH∽△A′B′H′,
归纳
相似三角形对应高的比等于相似比.
∴
合作探究
2、相似三角形对应角平分线的比等于相似比
例10 如图,已知△ABC∽△A′B′C′,AT,A′T′分别为对应角∠BAC=
∠B′A′C′的角平分线。求证: .
举
例
证明:∵△ABC∽△A′B′C′,
∴∠B=∠B′,∠BAC=∠B′A′C′.
又∵AT,A′T′分别平分∠BAC=∠B′A′C′,
∴△ABT∽△A′B′T′,
∴
∴∠BAT=∠B′A′T′,
∴∠BAT= ∠BAC,∠B′A′C′= ∠B′A′T′
归纳
相似三角形对应角平分线的比等于相似比.
合作探究
3、相似三角形对应中线的比等于相似比
已知△ABC∽△A′B′C′,若AD,A′D′分别为△ABC,△A′B′C′的中线,则 成立吗?由此你得出什么结论?
证明:∵△ABC∽△A′B′C′,
又AD,A′D′分别平分BC、B′C′,
∴△ABD∽△A′B′D′,
∴
议一议
∴BD= BC,B′D′= B′C′
归纳
相似三角形对应中线的比等于相似比.
∴∠B=∠B′,
∴
合作探究
例9 如图,AB//PQ,AB=100m,PQ=120m。点P,A,C在一条直线上,点Q,B,C也在一条直线上。若AB与PQ的距离是40m,求点C到直线PQ的距离。
解:过点C作CD⊥PQ,交PQ的延长线于D,交AB的延长线于E
∴△CAB∽△CPQ,CE⊥AB,DE=40m.
∵AB=100m,PQ=120m,CE=CD-DE,
∴CD=240m.
∴
举
例
∵AB//PQ,
答:点C到直线PQ的距离为240m.
∴
D
E
课堂练习
练习
1、要制作两个形状相同的三角形框架,其中一个三角形的三边长分别
为5cm,6cm和9cm,另一个三角形的最短边长为2.5cm,则它的最长边
为( )
A. 3cm B. 4cm C. 4.5cm D. 5cm
2、如下左图,四边形ABCD的对角线AC,BD相交于点O,AD//BC,G是BD的中点。若AD=3,BC=9,则GO︰BG等于( )
A. 1︰2 B. 1︰3 C. 2︰3 D. 11︰20
3、如上右图,在△ABC中,DE//BC, ,DE=6,则BC的长是 ;
C
A
18
课堂练习
练习
4、如图所示,某同学拿着一把刻有厘米分划的小尺,站在距旗杆约30m的地方,把手臂向前伸直且让小尺竖直,看到尺上大约有24个分划恰好遮住旗杆。已知此同学的臂长约为60cm,求旗杆的大致高度。
解:由已知得:BC=24cm=0.24m,CM=60cm=0.6m,
EN=30m,BC//DE,CM//EN,
∴△ABC∽△ADE,△ACM∽△AEN
∴DE=12m.
答:旗杆大致高12m.
课堂小结
通过本节课的学习,你有什么收获与体会?
动脑筋
作业设计
练习
1、已知△ABC∽△DEF,AM,DN分别为△ABC,△DEF的一条中线,且AM=6cm,AB=8cm,DE=4cm,求DN的长.
2、如图,△ABC∽△A′B′C′,AD,BE分别是△ABC的高和中线,A′D′,B′E′分别是△A′B′C′的高和中线,且AD=4,A′D′=3,BE=6,求B′E′的长.
DN=3cm
再 见
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
