4.4.2 解直角三角形的应用(2)(精讲课件)(共13张PPT)
文档属性
| 名称 | 4.4.2 解直角三角形的应用(2)(精讲课件)(共13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 794.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-22 17:02:14 | ||
图片预览





文档简介
(共13张PPT)
4.4.2 解直角三角形的应用(2)
湘教版数学九年级上册
同学们都登过山吗?我们在登山的时候,有的山坡登的比较轻松,有的山坡登的很吃力,这是为什么呢?又如何用数量关系来反映坡的倾斜程度呢?
情境导入
1、坡角、坡度的概念及关系
(1)坡度的概念:如图,从山坡脚下点A上坡走到点B时,升高的高度h(即线段BC的长)与水平前进的距离l(即线段AC的长度)的比叫作坡度,用字母i表示,即:
(2)坡度的表达形式:坡度通常写成1∶m的形式。
(3)坡角:山坡与地平面的夹角叫作坡角,如图:∠BAC。
(4)坡度i与坡角α之间的关系: ,显然坡度等于坡角的正切。
合作探究
1、坡角、坡度的概念及关系
[议一议]坡度、坡角越大,山坡越陡吗?
合作探究
例2 如图,一山坡的坡度i=1∶2,小刚从山坡脚下点A出发,沿山坡向上走了240m到达点C,这座山坡的坡角是多少度(精确到0.01°)?小刚上升了多少米(精确到0.1m)?
举
例
解:由已知得:
2、坡度、坡角的应用
分析:这是道实际应用问题,根据题意,△ABC是直角三角形,∠B=90°,斜坡的坡度i=1∶2,他上升了多少米,即求直角三角形的直角边BC的长,这座山坡的坡角是多少度,即求直角三角形的锐角∠A的度数。
∴∠A≈26.57°,
在Rt△ABC中,∠B=90°,∠A≈26.57°,AC=240m
答:这座山坡的坡角约为26.57°,小刚上升了约107.3m。
你还可以用其他方法求出BC吗?
典例解析
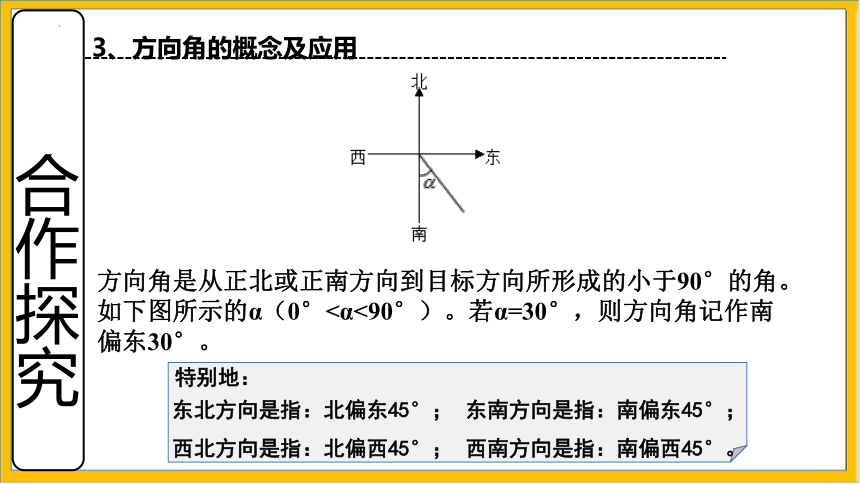
3、方向角的概念及应用
方向角是从正北或正南方向到目标方向所形成的小于90°的角。如下图所示的α(0°<α<90°)。若α=30°,则方向角记作南偏东30°。
东北方向是指:北偏东45°;
西北方向是指:北偏西45°;
东南方向是指:南偏东45°;
西南方向是指:南偏西45°。
特别地:
合作探究
例3 如图,一艘船以40km/h的速度向正东航行,在A处测得灯塔C在北偏东60°方向上,继续航行1h到达B处,这时测得灯塔C在北偏东30°方向上。已知在灯塔C的四周30km内有暗礁。问这艘船继续向东航行是否安全?
举
例
解:由已知得:∠CAB=90°-60°=30°,
∠CBD=90°-30°=60°,AB=40×1=40
3、方向角的概念及应用
在Rt△BDC中,
因此,该船能继续安全向东航行。
过点C作CD⊥AB,交AB的延长线于D
可设CD= x,则BD=x
在Rt△ADC中,
∴AD=3x
∵AB=AD-BD=40
∴3x-x=40
∴x=20
∴CD= x= >30
60°
30°
北
东
C
B
A
30°
60°
D
典例解析
3.如图,一艘轮船自西向东航行,航行到A处测得小岛C位于北偏东60°方向上,继续向东航行10海里到达点B处,测得小岛C在轮船的北偏东15°方向上,此时轮船与小岛C的距离为 海里.(结果保留根号)
1.如图,某幼儿园为了加强安全管理,决定将园内滑梯的倾斜角由45°降为30°,已知点D,B,C在同一水平地面上,且BD的长为2米,则改造后滑梯的长度是( )
A. B. C. D.
2.如图,一艘油轮在海中航行,在A点看到小岛B在A的北偏东25°方向距离60海里处,油轮沿北偏东70°方向航行到C处,看到小岛B在C的北偏西50°方向,则油轮从A航行到C处的距离是( )海里.(结果保留整数)(参考数据: ≈1.41, ≈1.74, ≈2.45)
A.66.8 B.67 C.115.8 D.116
D
60°
45°
60
x
x
2
D
30°
60°
45°
10
5
D
B
课堂练习
4.如图,点A、B、C表示某旅游景区三个缆车站的位置,线段AB、BC表示连接缆车站的钢缆,已知A、B、C三点在同一铅直平面内,它们的海拔高度AA′,BB′,CC′分别为110米、310米、710米,钢缆AB的坡度i1=1∶2,钢缆BC的坡度i2=1∶1,景区因改造缆车线路,需要从A到C直线架设一条钢缆,那么钢缆AC的长度是多少米?
课堂练习
5.如图,我渔政310船在南海海面上沿正东方向匀速航行,在A地观测到我渔船C在东北方向上的我国某传统渔场.若渔政310船航向不变,航行半小时后到达B处,此时观测到我渔船C在北偏东30°方向上.问渔政310船再航行多久,离我渔船C的距离最近?(假设我渔船C捕鱼时移动距离忽略不计,结果不取近似值.)
答:再航行 分钟离我渔船C的距离最近。
D
课堂练习
课堂小结
通过本节课的学习,你有什么收获与体会?
作业设计
1.一种等腰三角形坡屋顶的设计图如图所示.已知屋顶的宽度l为10m,坡屋顶的高度h为3.5m,求斜面AB的长度和坡角α(长度精确到0.1m,角度精确到1°).
2.某次军事演习中,有三艘船在同一时刻向指挥所报告:A船说B船在它的正东方向,C船在它的北偏东55°方向;B船说C船在它的北偏西35°方向;C船说它到A船的距离比它到B船的距离远40km.求A,B两船的距离(结果精确到0.1km).
α≈35°,AB≈6.1m.
AB≈162.9km.
再 见
4.4.2 解直角三角形的应用(2)
湘教版数学九年级上册
同学们都登过山吗?我们在登山的时候,有的山坡登的比较轻松,有的山坡登的很吃力,这是为什么呢?又如何用数量关系来反映坡的倾斜程度呢?
情境导入
1、坡角、坡度的概念及关系
(1)坡度的概念:如图,从山坡脚下点A上坡走到点B时,升高的高度h(即线段BC的长)与水平前进的距离l(即线段AC的长度)的比叫作坡度,用字母i表示,即:
(2)坡度的表达形式:坡度通常写成1∶m的形式。
(3)坡角:山坡与地平面的夹角叫作坡角,如图:∠BAC。
(4)坡度i与坡角α之间的关系: ,显然坡度等于坡角的正切。
合作探究
1、坡角、坡度的概念及关系
[议一议]坡度、坡角越大,山坡越陡吗?
合作探究
例2 如图,一山坡的坡度i=1∶2,小刚从山坡脚下点A出发,沿山坡向上走了240m到达点C,这座山坡的坡角是多少度(精确到0.01°)?小刚上升了多少米(精确到0.1m)?
举
例
解:由已知得:
2、坡度、坡角的应用
分析:这是道实际应用问题,根据题意,△ABC是直角三角形,∠B=90°,斜坡的坡度i=1∶2,他上升了多少米,即求直角三角形的直角边BC的长,这座山坡的坡角是多少度,即求直角三角形的锐角∠A的度数。
∴∠A≈26.57°,
在Rt△ABC中,∠B=90°,∠A≈26.57°,AC=240m
答:这座山坡的坡角约为26.57°,小刚上升了约107.3m。
你还可以用其他方法求出BC吗?
典例解析
3、方向角的概念及应用
方向角是从正北或正南方向到目标方向所形成的小于90°的角。如下图所示的α(0°<α<90°)。若α=30°,则方向角记作南偏东30°。
东北方向是指:北偏东45°;
西北方向是指:北偏西45°;
东南方向是指:南偏东45°;
西南方向是指:南偏西45°。
特别地:
合作探究
例3 如图,一艘船以40km/h的速度向正东航行,在A处测得灯塔C在北偏东60°方向上,继续航行1h到达B处,这时测得灯塔C在北偏东30°方向上。已知在灯塔C的四周30km内有暗礁。问这艘船继续向东航行是否安全?
举
例
解:由已知得:∠CAB=90°-60°=30°,
∠CBD=90°-30°=60°,AB=40×1=40
3、方向角的概念及应用
在Rt△BDC中,
因此,该船能继续安全向东航行。
过点C作CD⊥AB,交AB的延长线于D
可设CD= x,则BD=x
在Rt△ADC中,
∴AD=3x
∵AB=AD-BD=40
∴3x-x=40
∴x=20
∴CD= x= >30
60°
30°
北
东
C
B
A
30°
60°
D
典例解析
3.如图,一艘轮船自西向东航行,航行到A处测得小岛C位于北偏东60°方向上,继续向东航行10海里到达点B处,测得小岛C在轮船的北偏东15°方向上,此时轮船与小岛C的距离为 海里.(结果保留根号)
1.如图,某幼儿园为了加强安全管理,决定将园内滑梯的倾斜角由45°降为30°,已知点D,B,C在同一水平地面上,且BD的长为2米,则改造后滑梯的长度是( )
A. B. C. D.
2.如图,一艘油轮在海中航行,在A点看到小岛B在A的北偏东25°方向距离60海里处,油轮沿北偏东70°方向航行到C处,看到小岛B在C的北偏西50°方向,则油轮从A航行到C处的距离是( )海里.(结果保留整数)(参考数据: ≈1.41, ≈1.74, ≈2.45)
A.66.8 B.67 C.115.8 D.116
D
60°
45°
60
x
x
2
D
30°
60°
45°
10
5
D
B
课堂练习
4.如图,点A、B、C表示某旅游景区三个缆车站的位置,线段AB、BC表示连接缆车站的钢缆,已知A、B、C三点在同一铅直平面内,它们的海拔高度AA′,BB′,CC′分别为110米、310米、710米,钢缆AB的坡度i1=1∶2,钢缆BC的坡度i2=1∶1,景区因改造缆车线路,需要从A到C直线架设一条钢缆,那么钢缆AC的长度是多少米?
课堂练习
5.如图,我渔政310船在南海海面上沿正东方向匀速航行,在A地观测到我渔船C在东北方向上的我国某传统渔场.若渔政310船航向不变,航行半小时后到达B处,此时观测到我渔船C在北偏东30°方向上.问渔政310船再航行多久,离我渔船C的距离最近?(假设我渔船C捕鱼时移动距离忽略不计,结果不取近似值.)
答:再航行 分钟离我渔船C的距离最近。
D
课堂练习
课堂小结
通过本节课的学习,你有什么收获与体会?
作业设计
1.一种等腰三角形坡屋顶的设计图如图所示.已知屋顶的宽度l为10m,坡屋顶的高度h为3.5m,求斜面AB的长度和坡角α(长度精确到0.1m,角度精确到1°).
2.某次军事演习中,有三艘船在同一时刻向指挥所报告:A船说B船在它的正东方向,C船在它的北偏东55°方向;B船说C船在它的北偏西35°方向;C船说它到A船的距离比它到B船的距离远40km.求A,B两船的距离(结果精确到0.1km).
α≈35°,AB≈6.1m.
AB≈162.9km.
再 见
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
