14.3.2等腰三角形的判定[上学期]
文档属性
| 名称 | 14.3.2等腰三角形的判定[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 344.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-11-17 19:24:00 | ||
图片预览




文档简介
课件20张PPT。〖教学目标〗
◆认知目标:理解等腰三角形的判定方法的证明过程.
◆能力目标:通过定理的证明和应用,初步了解转化思想,并培养学生逻辑思维能力、分析问题和解决问题的能力.
◆情感目标:学生初步了解数学来源于实践,反过来又服务于实践的辨证唯物主义观点.
〖教学重点与难点〗
◆教学重点:等腰三角形的判定方法及其运用.
◆教学难点:等腰三角形判定方法证明中添加辅助线的思想方法以及等腰三角形性质与判定的区别.
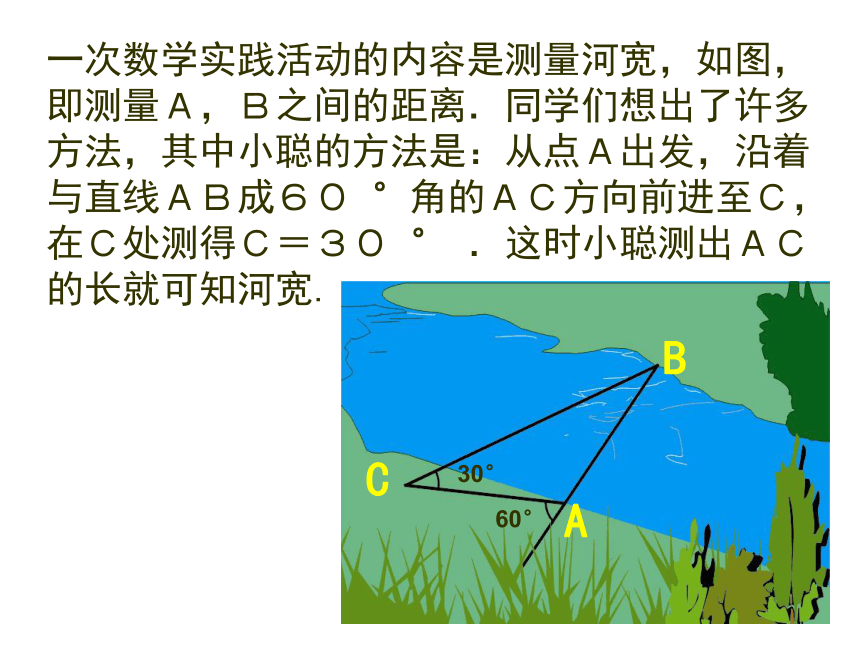
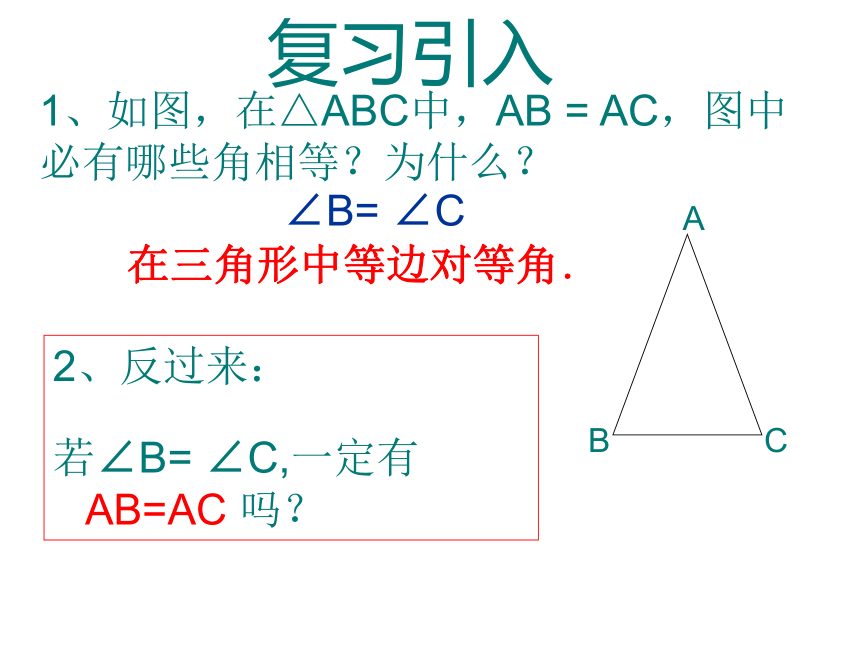
等腰三角形的判定一次数学实践活动的内容是测量河宽,如图,即测量A,B之间的距离.同学们想出了许多方法,其中小聪的方法是:从点A出发,沿着与直线AB成60 °角的AC方向前进至C,在C处测得C=30 ° .这时小聪测出AC的长就可知河宽.复习引入1、如图,在△ABC中,AB = AC,图中必有哪些角相等?为什么? 2、反过来:
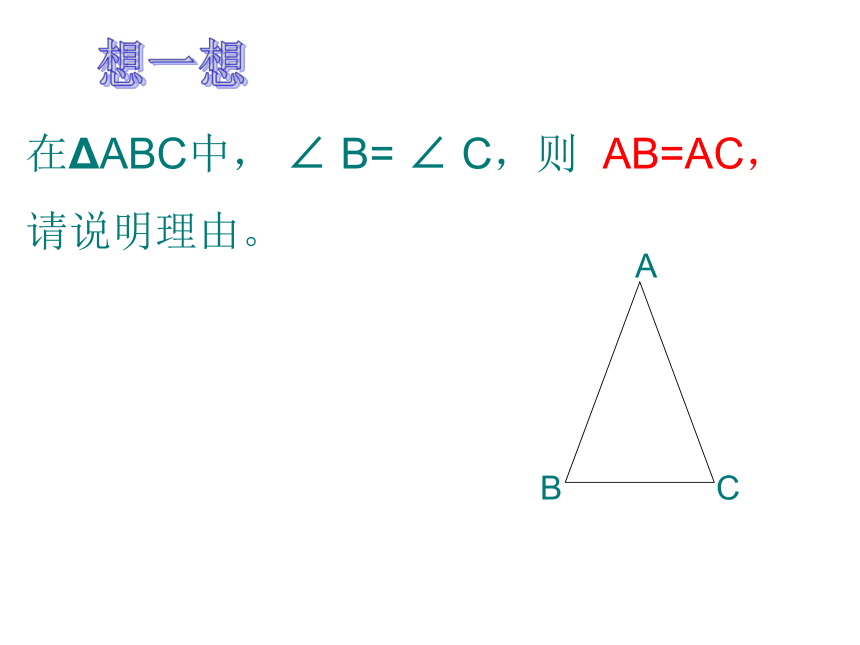
若∠B= ∠C,一定有AB=AC 吗?∠B= ∠C在三角形中等边对等角.在ΔABC中, ∠ B= ∠ C,则 AB=AC,
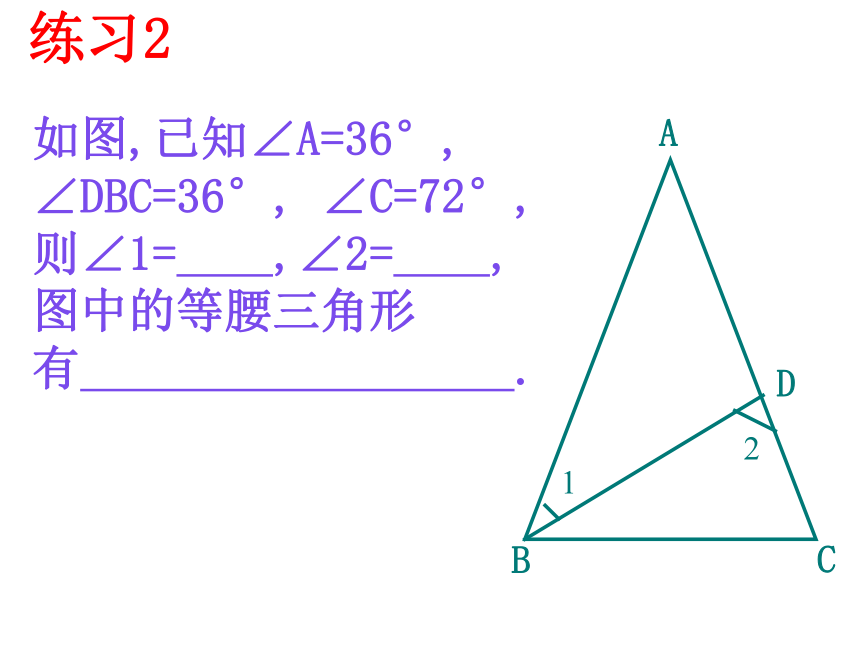
请说明理由。想一想练习1在△ABC中, 已知∠A=40°,∠B=70°,判断△ABC是什么三角形,为什么?练习2ABCD如图,已知∠A=36°, ∠DBC=36°, ∠C=72°,则∠1= ,∠2= , 图中的等腰三角形有 .12例2:上午10 时,一条船从A处出发以20海里每小时的速度向正北航行,中午12时到达B处,从A、B望灯塔C,测得∠NAC=40°, ∠NBC=80°求从B处到灯塔C的距离.NBAC80°40°北解:∵∠NBC=∠A+∠C
∴∠C=80°- 40°
= 40°= ∠A
∴ BA=BC(等角对等边)
∵AB=20(12-10)=40
∴BC=40
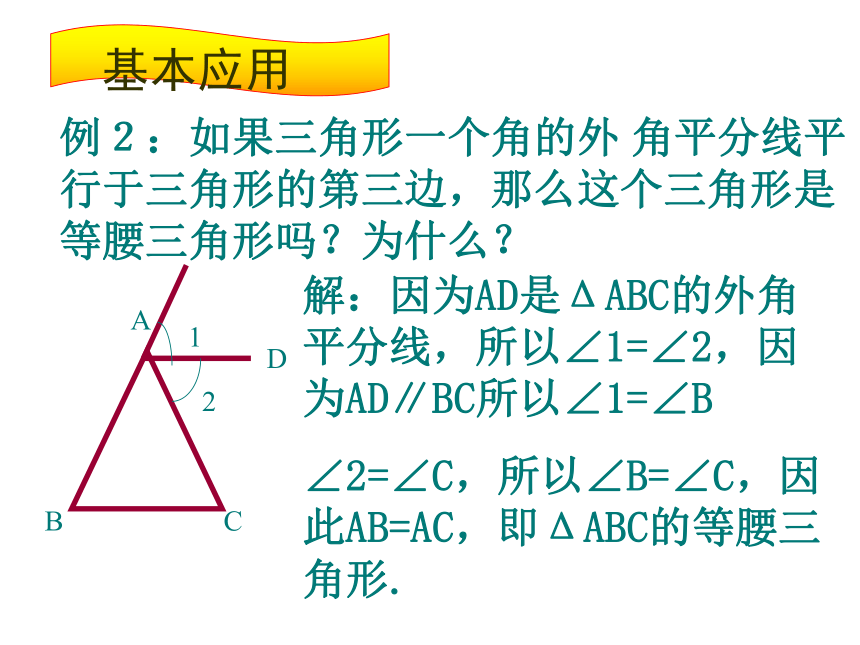
答:B处到达灯塔C40海里例2:如果三角形一个角的外 角平分线平行于三角形的第三边,那么这个三角形是等腰三角形吗?为什么?ABCD12解:因为AD是ΔABC的外角平分线,所以∠1=∠2,因为AD∥BC所以∠1=∠B
∠2=∠C,所以∠B=∠C,因此AB=AC,即ΔABC的等腰三角形.例3.如图,BD是等腰三角形ABC的底边AC上的高,DE∥BC,交AB于点E.判断△BDE是不是等腰三角形,并说明理由.练习41.已知:如图,AD∥BC,BD平分∠ABC,试判断△ABD的形状,并说明理由?练习52.如图,在等腰△ABC中,AB=AC,两底角的平分线BE和CD相交于点O,那么△OBC是什么三角形?为什么?ABCEDO小结有两边相等的三角形是等腰三角形。2.等边对等角,3. 三线合一。4.是轴对称图形.2.等角对等边,1.两边相等。1.两腰相等. 思考1:如图,在△ABC中,已知∠ABC=∠ACB,BF平分∠ABC,CF平分∠ACB,请想想看,由以上条件,你能推导出什么结论?并说明理由.ABCF与同伴交流你在探索思路的过程中的具体做法.下例各说法对吗?为什么?等腰三角形两底角的平分线相等.
等腰三角形两腰上的中线相等.
等腰三角形两腰上的高相等.
思考2:思考3 如图,折叠一张三角形纸片ABC,使点A落在BC边上的点F,且折痕DE//BC,如图,则三角形DBF和EFC是不是等腰三角形?EFD思考4 若一个三角形的三个内角分别为20度,40度,120度,你能把这个三角形分成两个等腰三角形吗? 你还有哪些疑问呢?通过这节课的学习,你有什么收获? 祝大家学习进步,天天开心.
◆认知目标:理解等腰三角形的判定方法的证明过程.
◆能力目标:通过定理的证明和应用,初步了解转化思想,并培养学生逻辑思维能力、分析问题和解决问题的能力.
◆情感目标:学生初步了解数学来源于实践,反过来又服务于实践的辨证唯物主义观点.
〖教学重点与难点〗
◆教学重点:等腰三角形的判定方法及其运用.
◆教学难点:等腰三角形判定方法证明中添加辅助线的思想方法以及等腰三角形性质与判定的区别.
等腰三角形的判定一次数学实践活动的内容是测量河宽,如图,即测量A,B之间的距离.同学们想出了许多方法,其中小聪的方法是:从点A出发,沿着与直线AB成60 °角的AC方向前进至C,在C处测得C=30 ° .这时小聪测出AC的长就可知河宽.复习引入1、如图,在△ABC中,AB = AC,图中必有哪些角相等?为什么? 2、反过来:
若∠B= ∠C,一定有AB=AC 吗?∠B= ∠C在三角形中等边对等角.在ΔABC中, ∠ B= ∠ C,则 AB=AC,
请说明理由。想一想练习1在△ABC中, 已知∠A=40°,∠B=70°,判断△ABC是什么三角形,为什么?练习2ABCD如图,已知∠A=36°, ∠DBC=36°, ∠C=72°,则∠1= ,∠2= , 图中的等腰三角形有 .12例2:上午10 时,一条船从A处出发以20海里每小时的速度向正北航行,中午12时到达B处,从A、B望灯塔C,测得∠NAC=40°, ∠NBC=80°求从B处到灯塔C的距离.NBAC80°40°北解:∵∠NBC=∠A+∠C
∴∠C=80°- 40°
= 40°= ∠A
∴ BA=BC(等角对等边)
∵AB=20(12-10)=40
∴BC=40
答:B处到达灯塔C40海里例2:如果三角形一个角的外 角平分线平行于三角形的第三边,那么这个三角形是等腰三角形吗?为什么?ABCD12解:因为AD是ΔABC的外角平分线,所以∠1=∠2,因为AD∥BC所以∠1=∠B
∠2=∠C,所以∠B=∠C,因此AB=AC,即ΔABC的等腰三角形.例3.如图,BD是等腰三角形ABC的底边AC上的高,DE∥BC,交AB于点E.判断△BDE是不是等腰三角形,并说明理由.练习41.已知:如图,AD∥BC,BD平分∠ABC,试判断△ABD的形状,并说明理由?练习52.如图,在等腰△ABC中,AB=AC,两底角的平分线BE和CD相交于点O,那么△OBC是什么三角形?为什么?ABCEDO小结有两边相等的三角形是等腰三角形。2.等边对等角,3. 三线合一。4.是轴对称图形.2.等角对等边,1.两边相等。1.两腰相等. 思考1:如图,在△ABC中,已知∠ABC=∠ACB,BF平分∠ABC,CF平分∠ACB,请想想看,由以上条件,你能推导出什么结论?并说明理由.ABCF与同伴交流你在探索思路的过程中的具体做法.下例各说法对吗?为什么?等腰三角形两底角的平分线相等.
等腰三角形两腰上的中线相等.
等腰三角形两腰上的高相等.
思考2:思考3 如图,折叠一张三角形纸片ABC,使点A落在BC边上的点F,且折痕DE//BC,如图,则三角形DBF和EFC是不是等腰三角形?EFD思考4 若一个三角形的三个内角分别为20度,40度,120度,你能把这个三角形分成两个等腰三角形吗? 你还有哪些疑问呢?通过这节课的学习,你有什么收获? 祝大家学习进步,天天开心.
