等腰三角形 习题精选3[上学期]
文档属性
| 名称 | 等腰三角形 习题精选3[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 754.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-01-24 14:10:00 | ||
图片预览


文档简介
等腰三角形 习题精选(三)
综合训练卷(90分钟,满分100分)
一、选择题(每小题4分,共36分)
1.下列命题中,假命题是. ()
A.等腰三角形被底边上的中线分成的两个三角形全等
B.底边相等的两个等腰直角三角形全等
C.高相等的两个等边三角形全等
D.腰相等的两个等腰三角形全等
2.在下列命题中,正确的命题有()
①有一个外角是120° 的等腰三角形是等边三角形
②有两个外角相等的等腰三角形是等边三角形
③有一边上的高也是这边上的中线的等腰三角形是等边三角形
④三个外角都相等的三角形是等边三角形
A.4个
B.3个
C.2个
D.1个
3.在ABC中,AB=AC,BC=5cm,作AB的垂直平分线交另一腰AC于D,连接BD,如果BCD的周长为17cm,则腰长为()
A.12cm
B.6cm
C.7cm
D.5cm
4.如果一个等腰三角形的一个底角比顶角大15°,那么顶角为()
A.45°
B.40°
C.50°
D.55°
5.等腰三角形腰上的高与底边上的夹角为,顶角为,那么有()
A.
B.
C.
D.
6.如图14-3-8所示,在 A月C中,AB=AC, B=36,D、是BC上两点,使 ADE= AED=2 BAD,则图中等腰三角形共有()
A.3个
B.4个
C.5个
D.6个
7.如图14-3-9所示,在 ABC中,AB=AC,BAC与 ACB的平分线相交于点D,ADC=115°,那么 CAB的大小是()
A.80°B.50°C.60° D.20°
8.如图14-3-10所示,D为等边ABC的AC边上的一点,BD=C正,l= 2,那么ADE是()
A.钝角三角形
B.直角三角形
C.等边三角形
D.不等边三角形
9.如果等腰三角形一腰上的高与另一个腰的夹角为45 °,那么,这个等腰三角形的底角为()
A.67.05°
B.22.5°
C.67.5°
D.22.5° 或67.5°
二、填空题(每小题4分,共20分)
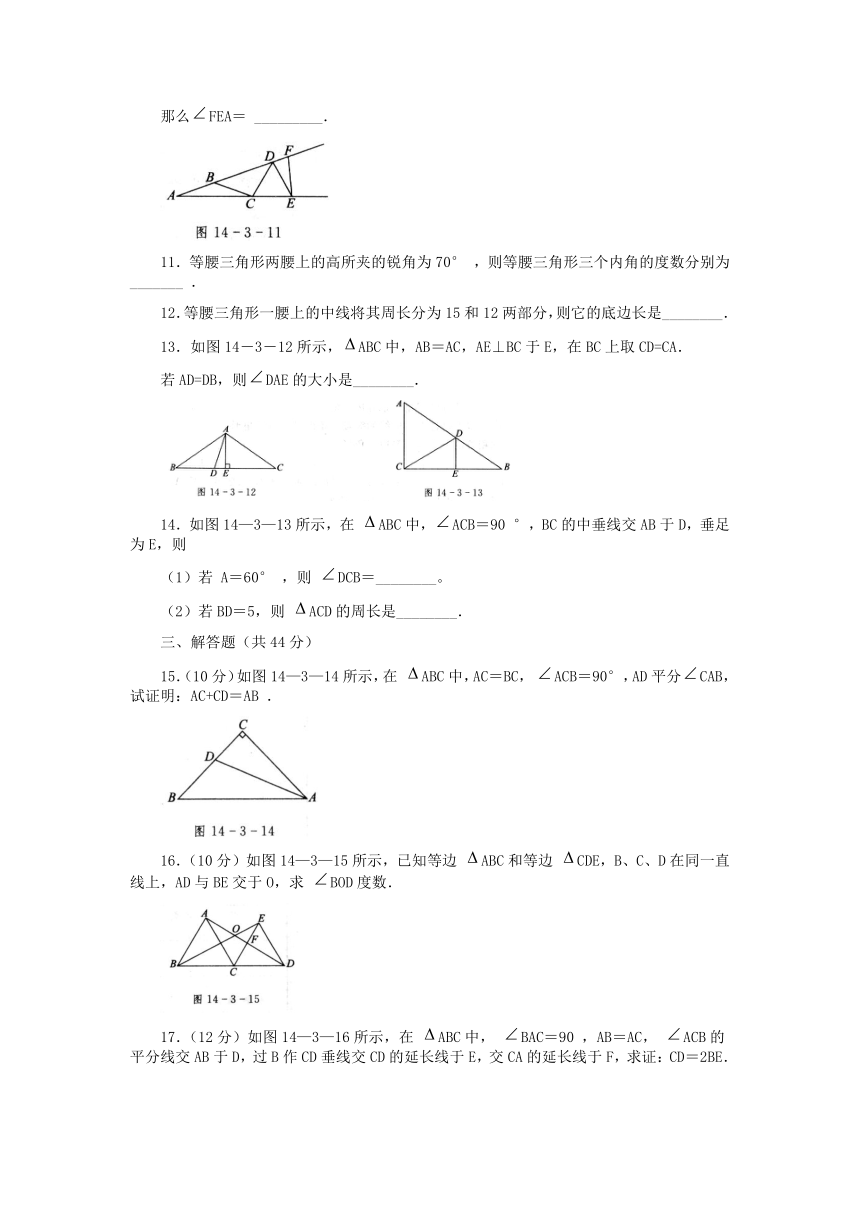
10.如图14-3-11所示,A=20°,AB=BC=CD=DE=EF,
那么FEA= _________.
11.等腰三角形两腰上的高所夹的锐角为70° ,则等腰三角形三个内角的度数分别为 _______ .
12.等腰三角形一腰上的中线将其周长分为15和12两部分,则它的底边长是________.
13.如图14-3-12所示,ABC中,AB=AC,AE⊥BC于E,在BC上取CD=CA.
若AD=DB,则DAE的大小是________.
14.如图14—3—13所示,在 ABC中,ACB=90 °,BC的中垂线交AB于D,垂足为E,则
(1)若 A=60° ,则 DCB=________。
(2)若BD=5,则 ACD的周长是________.
三、解答题(共44分)
15.(10分)如图14—3—14所示,在 ABC中,AC=BC, ACB=90°,AD平分CAB,试证明:AC+CD=AB .
16.(10分)如图14—3—15所示,已知等边 ABC和等边 CDE,B、C、D在同一直线上,AD与BE交于O,求 BOD度数.
17.(12分)如图14—3—16所示,在 ABC中, BAC=90 ,AB=AC, ACB的平分线交AB于D,过B作CD垂线交CD的延长线于E,交CA的延长线于F,求证:CD=2BE.
18.(12分)如图14—3—17所示,在ABC中,AD是BAC的平分线,AC=AB+BD,
求证: B=2 C.
答案
1.D
2.C
3.A
4.C
5.B
6.D
7.B
8.C
9.D
10.100°
11.55°,55°,70°或35°,35°,110°
12.7或11
13.18°
14.(1)30°(2)15°
15.如图D14—3—2所示,过点D作DF垂直AB,交A月于点正.
CAD≌EAD(ASA)
DE=CD,AC=AE
又BC=AC
B=45°
DE=BE
AC+CD=AE十BE=AB
16.ACD=ACE十ECD,ECB=ACE+ACB
ACD=ECB
ACD≌BCE(SAS)
BEC=ADC
又CFD=OFE
EOF=ECD=60°
BOD=120°
17.BF ⊥CE,CE是BCF的平分线
CEB≌CEF(ASA)
BE=EF
又BAC=90°,AB=AC
ECB=ECF=22.5°
FBA=EBC—ABC=(90°一22.5°)一45°=22.5°=ECF
BAF≌CAD(ASA)
CD=BF=2BE
18.如图D14—3—3所示在AE上截取AE=AB,连接DE.
AD是BAC的平分线
BAD=EAD(角平分线定义)
在ABD和AED中
ABD≌AED(SAS)
B=AED(全等三角形对应角相等)
BD=ED(全等三角形对应边相等)
BD=AC—A月=AC—AE=C正
ED=CE
EDC=C(等边对等角)
AED=EDC+C(三角形外角等于不相邻两内角之和)
B=2C
[解题点拨]
1.腰相等只有两条边相等,不能证明这两个三角形全等,还需要一条底边(SSS),或者夹角(SAS)
2.①、④项正确,②、③选项只能说明是等腰三角形,不能说明为等边三角形.
3.根据垂直平分线的性质,可知BD=AD,即BD+CD+BD=AC+BC= l7cm.
5.即
6. ABC, ABD, ADE,AEC,BAE,CAD.
8.易证ABD ≌ACE(SAS),可知AD=AE,且
CAE=BAD=60°
9.注意有两种情况,当顶角为锐角时,腰上的高在三角形内;当顶角为钝角时,腰上的高在三角形外.
10.ABC、BCD、CDE、EDF均为等腰三角形,它们底角相等,利用顶角的外角等于两底角之和的性质,可依次推出这些等腰三角形的顶角和底角大小.
11.等腰三角形两腰上的高所夹成两角,一角为70°,一角为110°,两条高与底边又形成了一个等腰三角形,即可分别求出各角的度数.
12.两部分周长,一部分是底边加腰的一半,另一部分是腰加上腰的一半,可能有两种情况,即腰加上腰的一半那部分周长可能是12,也可能是15,所以底边长也有7或11两种可能性.
13.DAC=CDA
又DAC=ABC十BAD=2ABC
DAC=2ABC=2ACB
DAC+CDA+ACB=180°
CDA=DAC=72°
DAE=18°
14.A=ACD,DCB=DBC
又 ACB=90°
DCB=30°
易证ACD为等边三角形AD=BD=5,故ACD周长为15 。
综合训练卷(90分钟,满分100分)
一、选择题(每小题4分,共36分)
1.下列命题中,假命题是. ()
A.等腰三角形被底边上的中线分成的两个三角形全等
B.底边相等的两个等腰直角三角形全等
C.高相等的两个等边三角形全等
D.腰相等的两个等腰三角形全等
2.在下列命题中,正确的命题有()
①有一个外角是120° 的等腰三角形是等边三角形
②有两个外角相等的等腰三角形是等边三角形
③有一边上的高也是这边上的中线的等腰三角形是等边三角形
④三个外角都相等的三角形是等边三角形
A.4个
B.3个
C.2个
D.1个
3.在ABC中,AB=AC,BC=5cm,作AB的垂直平分线交另一腰AC于D,连接BD,如果BCD的周长为17cm,则腰长为()
A.12cm
B.6cm
C.7cm
D.5cm
4.如果一个等腰三角形的一个底角比顶角大15°,那么顶角为()
A.45°
B.40°
C.50°
D.55°
5.等腰三角形腰上的高与底边上的夹角为,顶角为,那么有()
A.
B.
C.
D.
6.如图14-3-8所示,在 A月C中,AB=AC, B=36,D、是BC上两点,使 ADE= AED=2 BAD,则图中等腰三角形共有()
A.3个
B.4个
C.5个
D.6个
7.如图14-3-9所示,在 ABC中,AB=AC,BAC与 ACB的平分线相交于点D,ADC=115°,那么 CAB的大小是()
A.80°B.50°C.60° D.20°
8.如图14-3-10所示,D为等边ABC的AC边上的一点,BD=C正,l= 2,那么ADE是()
A.钝角三角形
B.直角三角形
C.等边三角形
D.不等边三角形
9.如果等腰三角形一腰上的高与另一个腰的夹角为45 °,那么,这个等腰三角形的底角为()
A.67.05°
B.22.5°
C.67.5°
D.22.5° 或67.5°
二、填空题(每小题4分,共20分)
10.如图14-3-11所示,A=20°,AB=BC=CD=DE=EF,
那么FEA= _________.
11.等腰三角形两腰上的高所夹的锐角为70° ,则等腰三角形三个内角的度数分别为 _______ .
12.等腰三角形一腰上的中线将其周长分为15和12两部分,则它的底边长是________.
13.如图14-3-12所示,ABC中,AB=AC,AE⊥BC于E,在BC上取CD=CA.
若AD=DB,则DAE的大小是________.
14.如图14—3—13所示,在 ABC中,ACB=90 °,BC的中垂线交AB于D,垂足为E,则
(1)若 A=60° ,则 DCB=________。
(2)若BD=5,则 ACD的周长是________.
三、解答题(共44分)
15.(10分)如图14—3—14所示,在 ABC中,AC=BC, ACB=90°,AD平分CAB,试证明:AC+CD=AB .
16.(10分)如图14—3—15所示,已知等边 ABC和等边 CDE,B、C、D在同一直线上,AD与BE交于O,求 BOD度数.
17.(12分)如图14—3—16所示,在 ABC中, BAC=90 ,AB=AC, ACB的平分线交AB于D,过B作CD垂线交CD的延长线于E,交CA的延长线于F,求证:CD=2BE.
18.(12分)如图14—3—17所示,在ABC中,AD是BAC的平分线,AC=AB+BD,
求证: B=2 C.
答案
1.D
2.C
3.A
4.C
5.B
6.D
7.B
8.C
9.D
10.100°
11.55°,55°,70°或35°,35°,110°
12.7或11
13.18°
14.(1)30°(2)15°
15.如图D14—3—2所示,过点D作DF垂直AB,交A月于点正.
CAD≌EAD(ASA)
DE=CD,AC=AE
又BC=AC
B=45°
DE=BE
AC+CD=AE十BE=AB
16.ACD=ACE十ECD,ECB=ACE+ACB
ACD=ECB
ACD≌BCE(SAS)
BEC=ADC
又CFD=OFE
EOF=ECD=60°
BOD=120°
17.BF ⊥CE,CE是BCF的平分线
CEB≌CEF(ASA)
BE=EF
又BAC=90°,AB=AC
ECB=ECF=22.5°
FBA=EBC—ABC=(90°一22.5°)一45°=22.5°=ECF
BAF≌CAD(ASA)
CD=BF=2BE
18.如图D14—3—3所示在AE上截取AE=AB,连接DE.
AD是BAC的平分线
BAD=EAD(角平分线定义)
在ABD和AED中
ABD≌AED(SAS)
B=AED(全等三角形对应角相等)
BD=ED(全等三角形对应边相等)
BD=AC—A月=AC—AE=C正
ED=CE
EDC=C(等边对等角)
AED=EDC+C(三角形外角等于不相邻两内角之和)
B=2C
[解题点拨]
1.腰相等只有两条边相等,不能证明这两个三角形全等,还需要一条底边(SSS),或者夹角(SAS)
2.①、④项正确,②、③选项只能说明是等腰三角形,不能说明为等边三角形.
3.根据垂直平分线的性质,可知BD=AD,即BD+CD+BD=AC+BC= l7cm.
5.即
6. ABC, ABD, ADE,AEC,BAE,CAD.
8.易证ABD ≌ACE(SAS),可知AD=AE,且
CAE=BAD=60°
9.注意有两种情况,当顶角为锐角时,腰上的高在三角形内;当顶角为钝角时,腰上的高在三角形外.
10.ABC、BCD、CDE、EDF均为等腰三角形,它们底角相等,利用顶角的外角等于两底角之和的性质,可依次推出这些等腰三角形的顶角和底角大小.
11.等腰三角形两腰上的高所夹成两角,一角为70°,一角为110°,两条高与底边又形成了一个等腰三角形,即可分别求出各角的度数.
12.两部分周长,一部分是底边加腰的一半,另一部分是腰加上腰的一半,可能有两种情况,即腰加上腰的一半那部分周长可能是12,也可能是15,所以底边长也有7或11两种可能性.
13.DAC=CDA
又DAC=ABC十BAD=2ABC
DAC=2ABC=2ACB
DAC+CDA+ACB=180°
CDA=DAC=72°
DAE=18°
14.A=ACD,DCB=DBC
又 ACB=90°
DCB=30°
易证ACD为等边三角形AD=BD=5,故ACD周长为15 。
