人教版数学八年级上册 13.3.2等边三角形(一)课件(共18张PPT)
文档属性
| 名称 | 人教版数学八年级上册 13.3.2等边三角形(一)课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 480.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-20 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
13.3.2等边三角形(一)
请你举出几个等边三角形的例子
A
B
C
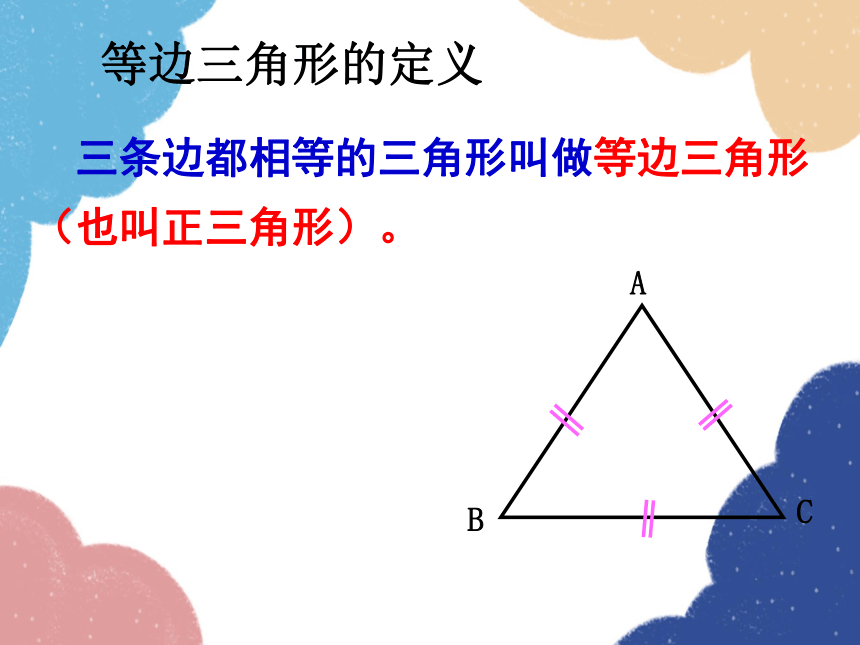
等边三角形的定义
三条边都相等的三角形叫做等边三角形(也叫正三角形)。
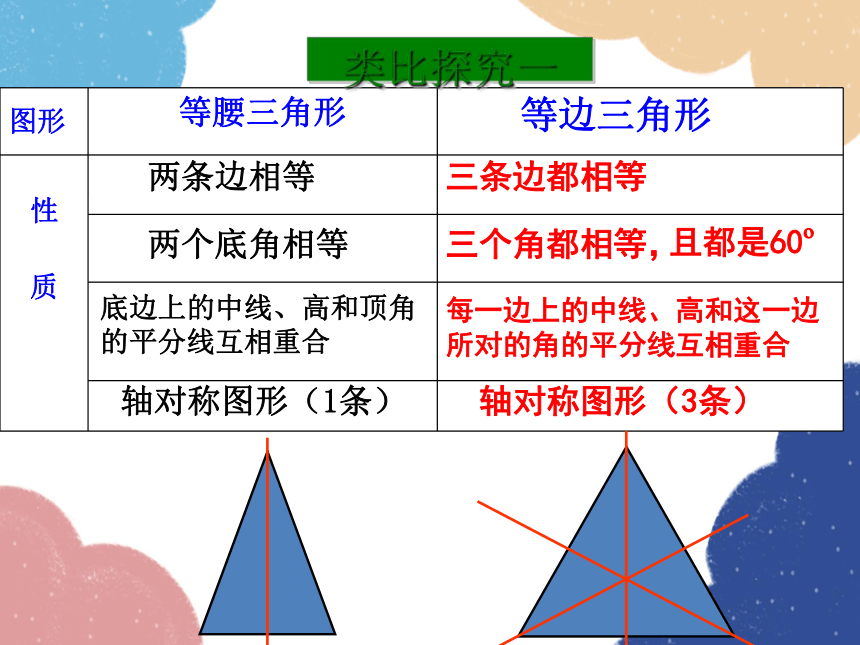
图形 等腰三角形
性 质
每一边上的中线、高和这一边所对的角的平分线互相重合
三个角都相等,
轴对称图形(3条)
等边三角形
轴对称图形(1条)
两个底角相等
底边上的中线、高和顶角的平分线互相重合
类比探究一
且都是60
两条边相等
三条边都相等
A
C
B
D
E
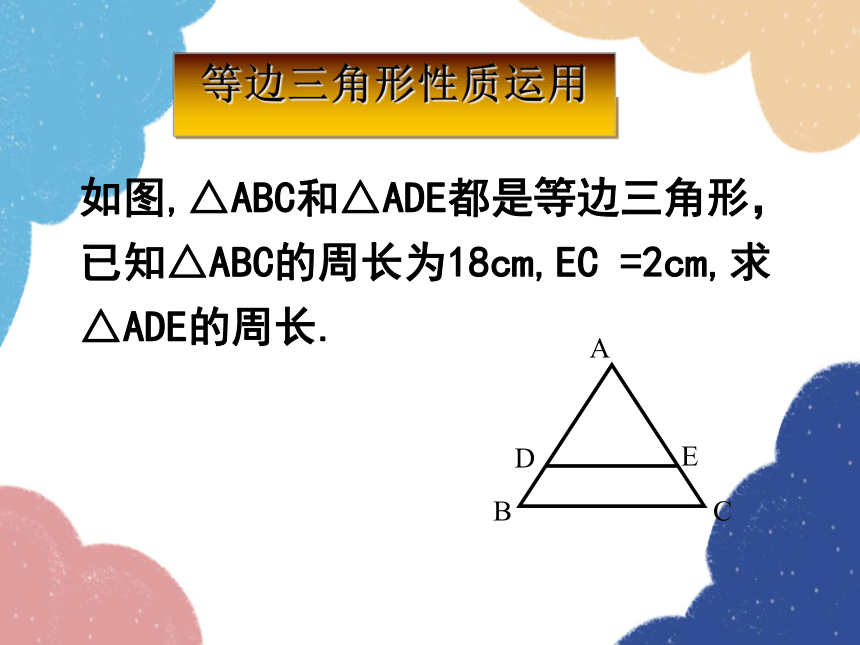
如图,△ABC和△ADE都是等边三角形,已知△ABC的周长为18cm,EC =2cm,求△ADE的周长.
等边三角形性质运用
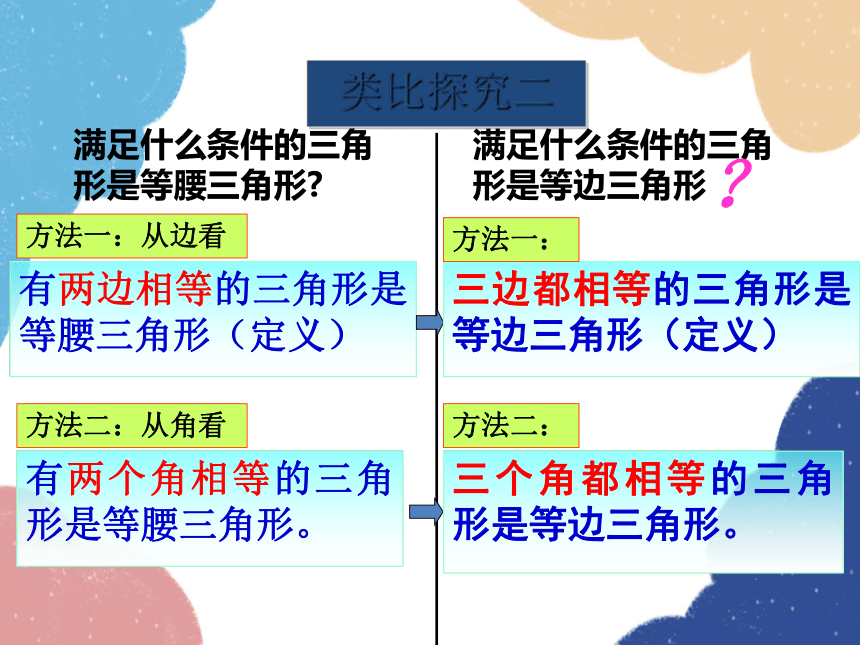
有两边相等的三角形是等腰三角形(定义)
有两个角相等的三角形是等腰三角形。
满足什么条件的三角形是等边三角形
?
满足什么条件的三角形是等腰三角形
类比探究二
三边都相等的三角形是等边三角形(定义)
三个角都相等的三角形是等边三角形。
方法一:从边看
方法二:从角看
方法一:
方法二:
小明认为还有第三种方法“两条边相等且有一个角是60°的三角形也是等边三角形”,
你同意吗?
想一想
等边三角形三种判定方法
三边都相等的三角形是等边三角形。
三个角都相等的三角形是等边三角形。
∵AB=BC=AC
∴△ABC是等边三角形
∵ ∠A= ∠ B= ∠ C
∴△ABC是等边三角形
∵ ∠A=600 , AB=BC
∴△ABC是等边三角形
有一个角是60°的等腰三角形是等边三角形。
例4:如图,在等边三角形ABC中,DE∥BC, 请问△ADE是等边三角形吗 试说明理由.
A
C
B
D
E
上题中,若将条件DE∥BC改为AD=AE, △ADE还是等边三角形吗 试说明理由.
变式练习
等边三角形判定运用
1、已知△ABC中,∠A=∠B=60°,AB=3cm,则△ABC的周长为______cm
9
2、如图:等边三角形ABC的三条角平分线交于点O,DE∥BC,则这个图形中的等腰三角形共有( )
A. 4个 B. 5个
C. 6个 D. 7个
D
A
C
B
D
E
O
B
C
D
A
E
3、如图,等边三角形ABC中,BD是AC边上的中线,BD=BE,求∠EDA的度数.
边相等转化为角相等
4、如图是由15根火柴组成的两个等边三角形,你能只移动三根火柴将此图变成四个等边三角形吗?
5、如图,△OAB和△OCD是两个全等的等边三角形,求∠AEB的大小.
C
B
O
D
A
E
D
C
A
B
E
O
如图,若△OAB和△OCD是两个不全等的等边三角形,你还能求出∠AEB的大小吗?
变式
(2) 等边三角形的性质:
1.等边三角形的内角都相等,且等于60 °
2.等边三角形是轴对称图形,有三条对称轴.
3.等边三角形各边上中线,高和所对角的平 分线都三线合一.
(3) 等边三角形的判定:
1.三边都相等的三角形是等边三角形.
2.三个角都相等的三角形是等边三角形.
3.有一个内角等于60 °的等腰三角形是等边三角形.
(1) 等边三角形的定义:
三条边都相等的三角形叫做等边三角形.
小结
边角互相转化思想
小结:
这节课你有何收获?还有哪些困惑?
同学们再见!
13.3.2等边三角形(一)
请你举出几个等边三角形的例子
A
B
C
等边三角形的定义
三条边都相等的三角形叫做等边三角形(也叫正三角形)。
图形 等腰三角形
性 质
每一边上的中线、高和这一边所对的角的平分线互相重合
三个角都相等,
轴对称图形(3条)
等边三角形
轴对称图形(1条)
两个底角相等
底边上的中线、高和顶角的平分线互相重合
类比探究一
且都是60
两条边相等
三条边都相等
A
C
B
D
E
如图,△ABC和△ADE都是等边三角形,已知△ABC的周长为18cm,EC =2cm,求△ADE的周长.
等边三角形性质运用
有两边相等的三角形是等腰三角形(定义)
有两个角相等的三角形是等腰三角形。
满足什么条件的三角形是等边三角形
?
满足什么条件的三角形是等腰三角形
类比探究二
三边都相等的三角形是等边三角形(定义)
三个角都相等的三角形是等边三角形。
方法一:从边看
方法二:从角看
方法一:
方法二:
小明认为还有第三种方法“两条边相等且有一个角是60°的三角形也是等边三角形”,
你同意吗?
想一想
等边三角形三种判定方法
三边都相等的三角形是等边三角形。
三个角都相等的三角形是等边三角形。
∵AB=BC=AC
∴△ABC是等边三角形
∵ ∠A= ∠ B= ∠ C
∴△ABC是等边三角形
∵ ∠A=600 , AB=BC
∴△ABC是等边三角形
有一个角是60°的等腰三角形是等边三角形。
例4:如图,在等边三角形ABC中,DE∥BC, 请问△ADE是等边三角形吗 试说明理由.
A
C
B
D
E
上题中,若将条件DE∥BC改为AD=AE, △ADE还是等边三角形吗 试说明理由.
变式练习
等边三角形判定运用
1、已知△ABC中,∠A=∠B=60°,AB=3cm,则△ABC的周长为______cm
9
2、如图:等边三角形ABC的三条角平分线交于点O,DE∥BC,则这个图形中的等腰三角形共有( )
A. 4个 B. 5个
C. 6个 D. 7个
D
A
C
B
D
E
O
B
C
D
A
E
3、如图,等边三角形ABC中,BD是AC边上的中线,BD=BE,求∠EDA的度数.
边相等转化为角相等
4、如图是由15根火柴组成的两个等边三角形,你能只移动三根火柴将此图变成四个等边三角形吗?
5、如图,△OAB和△OCD是两个全等的等边三角形,求∠AEB的大小.
C
B
O
D
A
E
D
C
A
B
E
O
如图,若△OAB和△OCD是两个不全等的等边三角形,你还能求出∠AEB的大小吗?
变式
(2) 等边三角形的性质:
1.等边三角形的内角都相等,且等于60 °
2.等边三角形是轴对称图形,有三条对称轴.
3.等边三角形各边上中线,高和所对角的平 分线都三线合一.
(3) 等边三角形的判定:
1.三边都相等的三角形是等边三角形.
2.三个角都相等的三角形是等边三角形.
3.有一个内角等于60 °的等腰三角形是等边三角形.
(1) 等边三角形的定义:
三条边都相等的三角形叫做等边三角形.
小结
边角互相转化思想
小结:
这节课你有何收获?还有哪些困惑?
同学们再见!
