14.3等腰三角形[上学期]
文档属性
| 名称 | 14.3等腰三角形[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 981.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-28 10:24:00 | ||
图片预览



文档简介
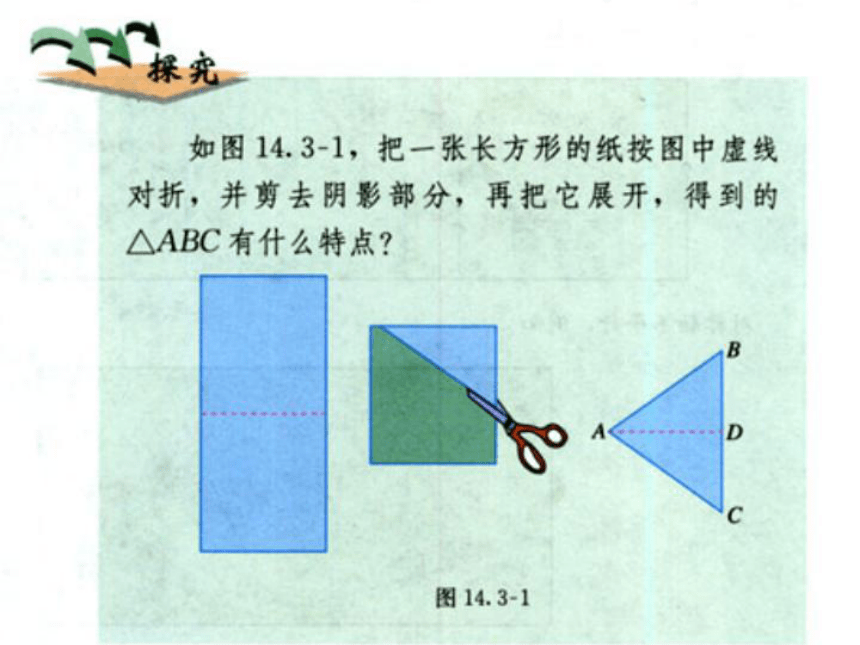
课件19张PPT。等腰三角形的性质14.3.1等腰三角形下载图片等腰三角形你知道什么是等腰三角形吗?什么叫等腰三角形?有两条边相等的三角形叫等腰三角形这个等腰三角形ABC的
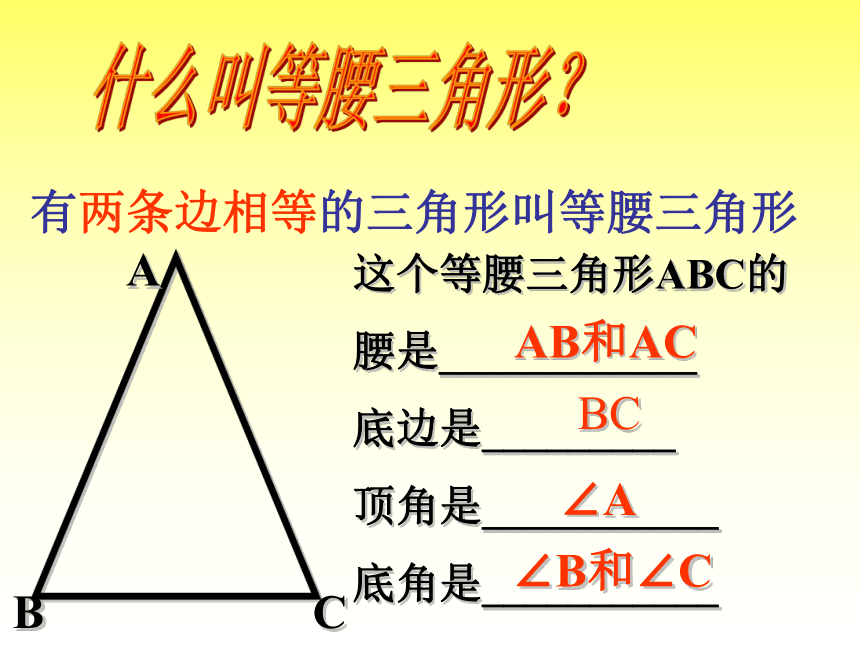
腰是____________
底边是_________
顶角是___________
底角是___________AB和ACBC∠A∠B和∠C大胆猜测 等腰三角形除了两腰相等以外,
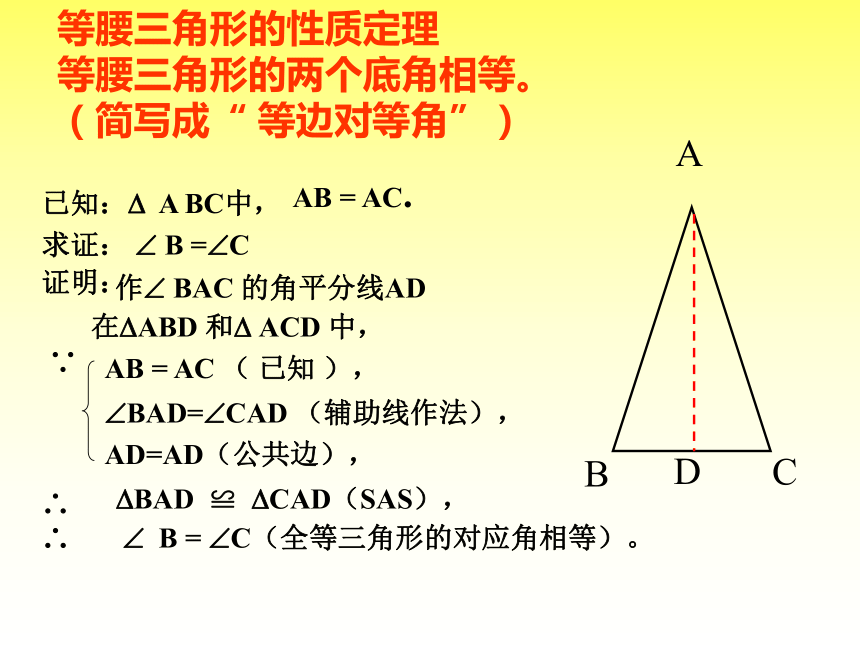
你还能发现什么?等腰三角形的性质定理
等腰三角形的两个底角相等。
(简写成“ 等边对等角”) AB = AC.? ? B = ?C(全等三角形的对应角相等)。
已知:? A BC中, 求证: ? B =?C证明:?BAD ≌ ?CAD(SAS), ? 作? BAC 的角平分线AD(1)作顶角∠ BAC的角平分线,使得∠1 = ∠ 2 , (2)作底边BC的中线 ,使得BD=CD , 用(SAS)用(SSS)用(HL) 等腰三角形顶角的平分线平分底边并且
垂直于底边。 猜想 即: AD 平分 BC,并且 AD ⊥ BC 。 (中线)(高)分析:等腰三角形的性质2: 等腰三角形顶角的平分线平分底边并且
垂直于底边。 等腰三角形的性质1:等腰三角形的两个底角相等 。
(简写成 “等边对等角”) 等腰三角形的性质 等腰三角形的顶角平分线,底边 上的
中线,底边上的高互相重合。(三线合一)由等腰三角形的性质2 可以知道, 等腰三角形性质
性质1 等腰三角形的两个底角相等(简
写成“等边对等角”);
性质2 等腰三角形的顶角平分线、底边
上的中线、底边上的高互相重合。
(可简记为“三线合一”)性质1: 在△ABC中, ∵ AB=AC ∴ ∠ABC=?ACB
性质2: ( 1 ) ∵ AB=AC AD是角平分线,
∴ ⊥ , ____=_____ ;
( 2) ∵ AB=AC AD是中线,
∴ ⊥ ,∴∠ = ∠____;
(3) ∵ AB=AC AD⊥BC,
∴∠_____=∠______,_____=______ 。
BAD CADBAD CAD
AD BCAD BCBD CDBD CD性质的应用格式:1 填空:在等腰三角形中,
(1)已知顶角为70°,其余两个角分别为_____。
(2)已知底角为70°,其余两个角分别为_____ 。
(3)已知一个角为70°, 其余两个角分别为______
(4)已知一个角为100°,其余两个角分别为_____ 。 55°, 55°70°, 40°55°, 55°或70°, 40°40°, 40°如图,△ABC是等腰直角三角形(AB=AC,∠BAC=90°)。AD是底边BC的高,标出∠ B, ∠ C, ∠ BAD, ∠ CAD的度数,图中有哪些相等的线段?ACB∟∟D45°45°45°45°相等的线段:
AB=AC
AD=BD=CD变式:在△ABC中,AB=AD=DC,∠BAD=26°,求∠ B 和∠ C的度数。DCBA小 结:小 结:1、等腰三角形的性质2、等腰三角形作辅助线最常用的方法例2 已知,如图AB=AC,AD=AE。求证:BD=CE。EDCBA方法一:
证明: ∵AB=AC
∴∠B=∠C(等边对等角)
同理:∠ADE=∠AEC
又∵ ∠ADE+∠ADB=180°
∠AED+∠AEC=180 °
∠ADB=∠AEC(等角的补角相等)
在△ABD与△ ACD中
∵ ∠B=∠C
∠ADB=∠AEC
AD=AE
∴ △ ABD≌ △ ACE(AAS)
∴ BD=CE方法二:
过A作AF⊥BC垂足为F点,
∵ AB=AC
∴BF=FC(三线合一)
同理:DF=EF
∴BF-DF=FC-EF
即BD=CEF∟方法三:
证明△ ABE≌ △ ACD下完例2 已知,如图AB=AC,AD=AE。求证:BD=CE。EDCBA方法三:
过A作AF⊥BC垂足为F点,
∵ AB=AC
∴BF=FC(三线合一)
同理:DF=EF
∴BF-DF=FC-EF
即BD=CEF∟
回再见
腰是____________
底边是_________
顶角是___________
底角是___________AB和ACBC∠A∠B和∠C大胆猜测 等腰三角形除了两腰相等以外,
你还能发现什么?等腰三角形的性质定理
等腰三角形的两个底角相等。
(简写成“ 等边对等角”) AB = AC.? ? B = ?C(全等三角形的对应角相等)。
已知:? A BC中, 求证: ? B =?C证明:?BAD ≌ ?CAD(SAS), ? 作? BAC 的角平分线AD(1)作顶角∠ BAC的角平分线,使得∠1 = ∠ 2 , (2)作底边BC的中线 ,使得BD=CD , 用(SAS)用(SSS)用(HL) 等腰三角形顶角的平分线平分底边并且
垂直于底边。 猜想 即: AD 平分 BC,并且 AD ⊥ BC 。 (中线)(高)分析:等腰三角形的性质2: 等腰三角形顶角的平分线平分底边并且
垂直于底边。 等腰三角形的性质1:等腰三角形的两个底角相等 。
(简写成 “等边对等角”) 等腰三角形的性质 等腰三角形的顶角平分线,底边 上的
中线,底边上的高互相重合。(三线合一)由等腰三角形的性质2 可以知道, 等腰三角形性质
性质1 等腰三角形的两个底角相等(简
写成“等边对等角”);
性质2 等腰三角形的顶角平分线、底边
上的中线、底边上的高互相重合。
(可简记为“三线合一”)性质1: 在△ABC中, ∵ AB=AC ∴ ∠ABC=?ACB
性质2: ( 1 ) ∵ AB=AC AD是角平分线,
∴ ⊥ , ____=_____ ;
( 2) ∵ AB=AC AD是中线,
∴ ⊥ ,∴∠ = ∠____;
(3) ∵ AB=AC AD⊥BC,
∴∠_____=∠______,_____=______ 。
BAD CADBAD CAD
AD BCAD BCBD CDBD CD性质的应用格式:1 填空:在等腰三角形中,
(1)已知顶角为70°,其余两个角分别为_____。
(2)已知底角为70°,其余两个角分别为_____ 。
(3)已知一个角为70°, 其余两个角分别为______
(4)已知一个角为100°,其余两个角分别为_____ 。 55°, 55°70°, 40°55°, 55°或70°, 40°40°, 40°如图,△ABC是等腰直角三角形(AB=AC,∠BAC=90°)。AD是底边BC的高,标出∠ B, ∠ C, ∠ BAD, ∠ CAD的度数,图中有哪些相等的线段?ACB∟∟D45°45°45°45°相等的线段:
AB=AC
AD=BD=CD变式:在△ABC中,AB=AD=DC,∠BAD=26°,求∠ B 和∠ C的度数。DCBA小 结:小 结:1、等腰三角形的性质2、等腰三角形作辅助线最常用的方法例2 已知,如图AB=AC,AD=AE。求证:BD=CE。EDCBA方法一:
证明: ∵AB=AC
∴∠B=∠C(等边对等角)
同理:∠ADE=∠AEC
又∵ ∠ADE+∠ADB=180°
∠AED+∠AEC=180 °
∠ADB=∠AEC(等角的补角相等)
在△ABD与△ ACD中
∵ ∠B=∠C
∠ADB=∠AEC
AD=AE
∴ △ ABD≌ △ ACE(AAS)
∴ BD=CE方法二:
过A作AF⊥BC垂足为F点,
∵ AB=AC
∴BF=FC(三线合一)
同理:DF=EF
∴BF-DF=FC-EF
即BD=CEF∟方法三:
证明△ ABE≌ △ ACD下完例2 已知,如图AB=AC,AD=AE。求证:BD=CE。EDCBA方法三:
过A作AF⊥BC垂足为F点,
∵ AB=AC
∴BF=FC(三线合一)
同理:DF=EF
∴BF-DF=FC-EF
即BD=CEF∟
回再见
