【新课标】3.2用频率估计概率 课件(共26张PPT)
文档属性
| 名称 | 【新课标】3.2用频率估计概率 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-21 17:20:19 | ||
图片预览






文档简介
(共26张PPT)
3.2用频率估计概率
北师大版九年级上册
教学目标
1、经历试验、统计等活动,感受随机现象的特点,进一步发展交流合作的意识和能力。
2、能用实验频率估计一些随机事件发生的概率,进一步体会概率的意义。
情景导入
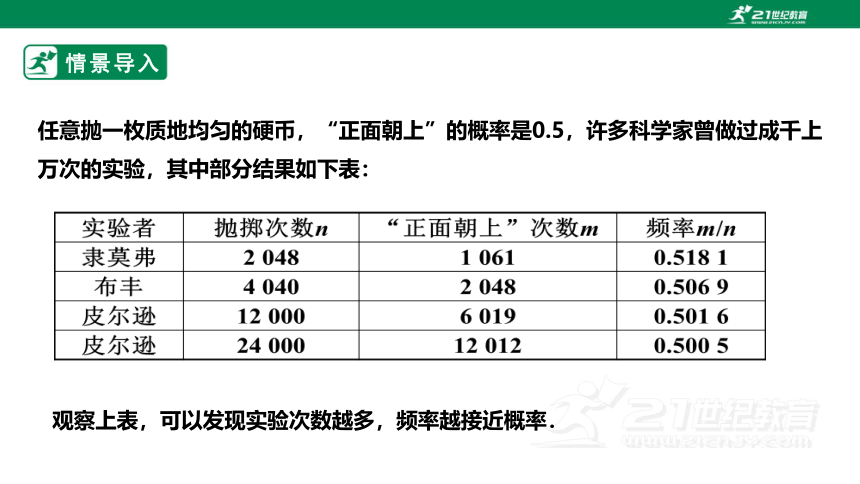
任意抛一枚质地均匀的硬币,“正面朝上”的概率是0.5,许多科学家曾做过成千上万次的实验,其中部分结果如下表:
观察上表,可以发现实验次数越多,频率越接近概率.
新知讲解
400个同学中,一定有2人的生日相同(可以不同年)吗?
一定.可以用“抽屉原理”加以解释.
例如,“一年最多366天,400个同学中一定会出现至少2人出生在同月同日,相当于400个物品放到366个抽屉里,一定至少有2个物品放在同一抽屉里——抽屉原理:把m个物品任意放进n个空抽屉(m>n),那么一定有一个抽屉中放进了至少2个物品”.
新知讲解
同意.
不一定.但有2个同学的生日相同的可能性较大.
300个同学中,一定有2人的生日相同吗?
可有人说:50个人中有2人生日相同的概率,你同意这种说法吗?
议一议
为了说明上述说法正确与否,我们可以通过大量重复试验,用“50个人中有2个人的生日相同”的频率来估计这一事件的概率。请你设计试验方案,并与同伴交流。
议一议
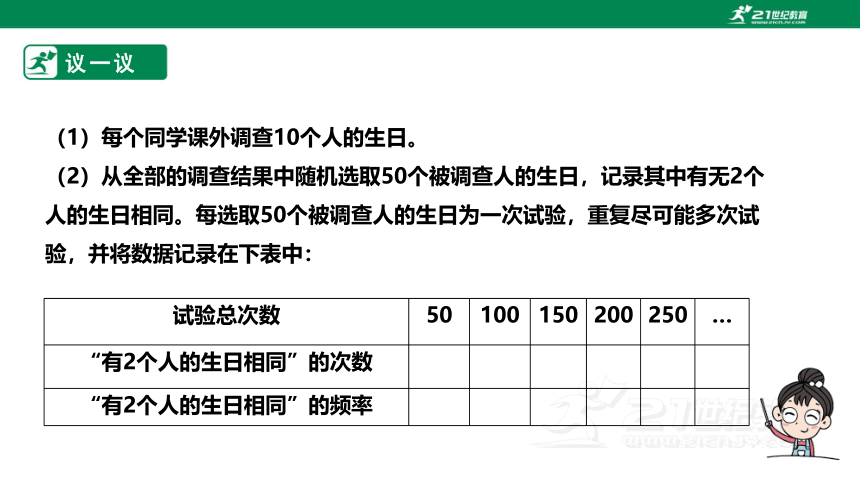
(1)每个同学课外调查10个人的生日。
(2)从全部的调查结果中随机选取50个被调查人的生日,记录其中有无2个人的生日相同。每选取50个被调查人的生日为一次试验,重复尽可能多次试验,并将数据记录在下表中:
试验总次数 50 100 150 200 250 …
“有2个人的生日相同”的次数
“有2个人的生日相同”的频率
议一议
“50人中有2人生日相同”的频率=
(3)根据上表中的数据,估计“50个人中有2个人的生日相同”的概率。
新知讲解
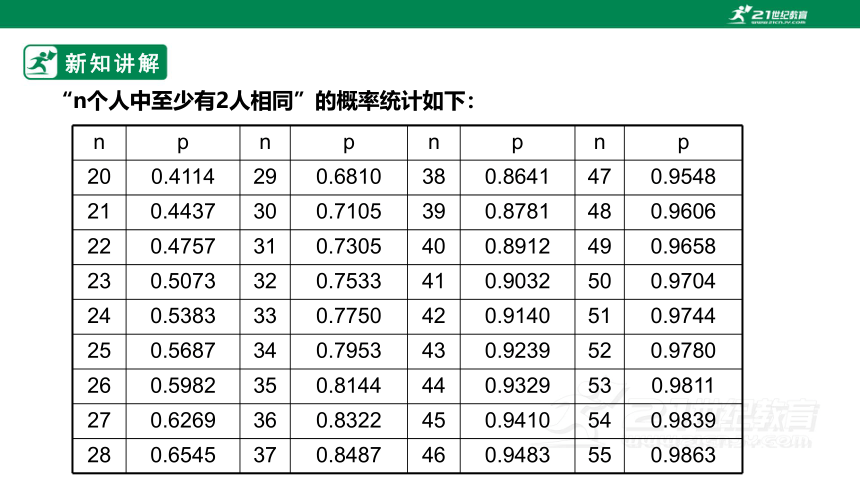
“n个人中至少有2人相同”的概率统计如下:
n p n p n p n p
20 0.4114 29 0.6810 38 0.8641 47 0.9548
21 0.4437 30 0.7105 39 0.8781 48 0.9606
22 0.4757 31 0.7305 40 0.8912 49 0.9658
23 0.5073 32 0.7533 41 0.9032 50 0.9704
24 0.5383 33 0.7750 42 0.9140 51 0.9744
25 0.5687 34 0.7953 43 0.9239 52 0.9780
26 0.5982 35 0.8144 44 0.9329 53 0.9811
27 0.6269 36 0.8322 45 0.9410 54 0.9839
28 0.6545 37 0.8487 46 0.9483 55 0.9863
归纳总结
(1)用频率估计概率:当试验次数足够大时,随机事件出现的频率稳定于相应的理论概率附近;
(2)用频率估计概率的条件:试验的次数必须足够大.
(3)计算方法:一般地,在大量重复试验中,如果事件A发生的频率稳定于某个常数p,那么估计事件A 发生的概率P(A)=p.
想一想
(1)一个口袋中有3个红球、7个白球,这些球除颜色外都相同,从口袋中随机摸出一个球,这个球是红球的概率是多少
(2)一个口袋中有红球、白球共10个,这些球除颜色外都相同,如果不将球倒出来数,那么你能设计一个试验方案,估计其中红球与白球的比例吗?
想一想
(1)每次随机摸出1个球并记录颜色,然后将球放回,搅匀,当次数越多,试验频率将越稳定于理论概率.
(2)每次随机摸出6个球,并记录其中红球与白球的比例,然后将球放回,搅匀,当次数越多,试验频率将越稳定于理论概率.
新知讲解
思考:频率与概率有什么区别与联系?
所谓频率,是在相同条件下进行重复试验时事件发生的次数与试验总次数的比值,其本身是随机的,在试验前不能够确定,且随着试验的不同而发生改变.
而一个随机事件发生的概率是确定的常数,是客观存在的,与试验次数无关.
归纳总结
频率与概率的关系
联系: 频率 概率
事件发生的频繁程度
事件发生的
可能性大小
在实际问题中,若事件的概率未知,常用频率作为它的估计值.
区别:频率本身是随机的,在试验前不能确定,做同样次数或不同次数的重复试验得到的事件的频率都可能不同,而概率是一个确定数,是客观存在的,与每次试验无关.
稳定性
大量重复试验
典例精析
例、 六一期间,某公园游戏场举行“迎奥运”活动.有一种游戏的规则是:在一个装有6个红球和若干个白球(每个球除颜色外其他都相同)的不透明的袋中,随机摸一个球,摸到一个红球就得到一个奥运福娃玩具.已知参加这种游戏活动的人数为40 000人次,公园游戏场发放的福娃玩具为10 000个.
(1)求参加一次这种游戏活动得到福娃玩具的频率;
(2)请你估计袋中白球有多少个.
典例精析
方法指导:(1)由40 000人次中公园游戏场发放的福娃玩具为10 000个,结合频率的意义可直接求得;(2)由概率与频率的关系可估计从袋中任意摸出一个球,恰好是红球的概率,从而引进未知数,构造方程求解.
解:(1)∵=,
∴参加一次这种游戏活动得到福娃玩具的频率为
典例精析
(2)∵试验次数很大时,频率接近于理论概率,
∴估计从袋中任意摸出一个球,恰好是红球的概率是.
设袋中白球有 x 个.
根据题意,得x+=,
解得x=18,
经检验,x=18是原分式方程的解,且符合题意,
∴估计袋中白球有18个.
课堂练习
1.不透明的袋子里放有4个黑球和若干个白球(这些球除颜色外都相同),老师将全班学生分成10个小组,进行摸球试验,经过大量重复摸球试验,统计显示,从中摸出白球的频率稳定在0.2附近,则袋子中白球的个数是 ( )
A.1 B.2 C.3 D.4
2.甲、乙两名同学在一次用频率估计概率的试验中统计了某一结果出现的频率,绘出的统计图如图所示,则符合这一结果的试验可能是 ( )
A.掷一枚正六面体的骰子,出现1点的概率
B.任意写一个整数,它能被2整除的概率
C.抛一枚质地均匀的硬币,出现正面朝上的概率
D.从一个装有2个白球和1个红球的袋子中任取1个球,取到红球的概率
A
D
课堂练习
3.下表记录了某种幼树在一定条件下移植成活的情况:
移植总数n 400 1500 3500 7000 9000 14000
成活数m 325 1336 3203 6335 8073 12628
成活的频率(精确到0.01) 0.813 0.891 0.915 0.905 0.897 0.902
由此估计这种幼树在此条件下移植成活的概率是_____(精确到0.1).
0.9
课堂练习
(1)请估计:当n很大时,摸到白球的频率将会接近 (精确到0.1);
(2)假如你摸一次,估计你摸到白球的概率P(白球)= .
0.6
0.6
摸球的次数n 100 200 300 500 800 1000 3000
摸到白球次数m 65 124 178 302 481 599 1803
摸到白球概率 0.65 0.62 0.593 0.604 0.601 0.599 0.601
4.在一个不透明的盒子里装有除颜色不同其余均相同的黑、白两种球,其中白球24个,黑球若干.小兵将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是试验中的一组统计数据:
课堂练习
5.某池塘里养了鱼苗10万条,根据这几年的经验知道,鱼苗成活率为95%,一段时间准备打捞出售,第一网捞出40条,称得平均每条鱼重 2.5千克,第二网捞出25条,称得平均每条鱼重2.2千克,第三网捞出35条,称得平均每条鱼重2.8千克,试估计这池塘中鱼的重量.
解:先计算每条鱼的平均重量是:
(2.5×40+2.2×25+2.8×35)÷(40+25+35)=2.53(千克);
所以这池塘中鱼的重量是2.53×100000× 95%=240350(千克).
课堂总结
频率估计概率
大量重复试验
求非等可能性事件概率
列举法
不能适应
频率稳定
常数附近
统计思想
用样本(频率)估计总体(概率)
一种关系
频率与概率的关系
频率稳定时可看作是概
率但概率与频率无关
板书设计
课题:3.2用频率估计概率
当试验次数很多或试验时样本容量足够大时,一件事件发生的频率与相应的概率会非常接近.此时,我们可以用一件事件发生的频率来估计这一事件发生的概率.
作业布置
课本P71 习题3.4 第1,2题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
3.2用频率估计概率
北师大版九年级上册
教学目标
1、经历试验、统计等活动,感受随机现象的特点,进一步发展交流合作的意识和能力。
2、能用实验频率估计一些随机事件发生的概率,进一步体会概率的意义。
情景导入
任意抛一枚质地均匀的硬币,“正面朝上”的概率是0.5,许多科学家曾做过成千上万次的实验,其中部分结果如下表:
观察上表,可以发现实验次数越多,频率越接近概率.
新知讲解
400个同学中,一定有2人的生日相同(可以不同年)吗?
一定.可以用“抽屉原理”加以解释.
例如,“一年最多366天,400个同学中一定会出现至少2人出生在同月同日,相当于400个物品放到366个抽屉里,一定至少有2个物品放在同一抽屉里——抽屉原理:把m个物品任意放进n个空抽屉(m>n),那么一定有一个抽屉中放进了至少2个物品”.
新知讲解
同意.
不一定.但有2个同学的生日相同的可能性较大.
300个同学中,一定有2人的生日相同吗?
可有人说:50个人中有2人生日相同的概率,你同意这种说法吗?
议一议
为了说明上述说法正确与否,我们可以通过大量重复试验,用“50个人中有2个人的生日相同”的频率来估计这一事件的概率。请你设计试验方案,并与同伴交流。
议一议
(1)每个同学课外调查10个人的生日。
(2)从全部的调查结果中随机选取50个被调查人的生日,记录其中有无2个人的生日相同。每选取50个被调查人的生日为一次试验,重复尽可能多次试验,并将数据记录在下表中:
试验总次数 50 100 150 200 250 …
“有2个人的生日相同”的次数
“有2个人的生日相同”的频率
议一议
“50人中有2人生日相同”的频率=
(3)根据上表中的数据,估计“50个人中有2个人的生日相同”的概率。
新知讲解
“n个人中至少有2人相同”的概率统计如下:
n p n p n p n p
20 0.4114 29 0.6810 38 0.8641 47 0.9548
21 0.4437 30 0.7105 39 0.8781 48 0.9606
22 0.4757 31 0.7305 40 0.8912 49 0.9658
23 0.5073 32 0.7533 41 0.9032 50 0.9704
24 0.5383 33 0.7750 42 0.9140 51 0.9744
25 0.5687 34 0.7953 43 0.9239 52 0.9780
26 0.5982 35 0.8144 44 0.9329 53 0.9811
27 0.6269 36 0.8322 45 0.9410 54 0.9839
28 0.6545 37 0.8487 46 0.9483 55 0.9863
归纳总结
(1)用频率估计概率:当试验次数足够大时,随机事件出现的频率稳定于相应的理论概率附近;
(2)用频率估计概率的条件:试验的次数必须足够大.
(3)计算方法:一般地,在大量重复试验中,如果事件A发生的频率稳定于某个常数p,那么估计事件A 发生的概率P(A)=p.
想一想
(1)一个口袋中有3个红球、7个白球,这些球除颜色外都相同,从口袋中随机摸出一个球,这个球是红球的概率是多少
(2)一个口袋中有红球、白球共10个,这些球除颜色外都相同,如果不将球倒出来数,那么你能设计一个试验方案,估计其中红球与白球的比例吗?
想一想
(1)每次随机摸出1个球并记录颜色,然后将球放回,搅匀,当次数越多,试验频率将越稳定于理论概率.
(2)每次随机摸出6个球,并记录其中红球与白球的比例,然后将球放回,搅匀,当次数越多,试验频率将越稳定于理论概率.
新知讲解
思考:频率与概率有什么区别与联系?
所谓频率,是在相同条件下进行重复试验时事件发生的次数与试验总次数的比值,其本身是随机的,在试验前不能够确定,且随着试验的不同而发生改变.
而一个随机事件发生的概率是确定的常数,是客观存在的,与试验次数无关.
归纳总结
频率与概率的关系
联系: 频率 概率
事件发生的频繁程度
事件发生的
可能性大小
在实际问题中,若事件的概率未知,常用频率作为它的估计值.
区别:频率本身是随机的,在试验前不能确定,做同样次数或不同次数的重复试验得到的事件的频率都可能不同,而概率是一个确定数,是客观存在的,与每次试验无关.
稳定性
大量重复试验
典例精析
例、 六一期间,某公园游戏场举行“迎奥运”活动.有一种游戏的规则是:在一个装有6个红球和若干个白球(每个球除颜色外其他都相同)的不透明的袋中,随机摸一个球,摸到一个红球就得到一个奥运福娃玩具.已知参加这种游戏活动的人数为40 000人次,公园游戏场发放的福娃玩具为10 000个.
(1)求参加一次这种游戏活动得到福娃玩具的频率;
(2)请你估计袋中白球有多少个.
典例精析
方法指导:(1)由40 000人次中公园游戏场发放的福娃玩具为10 000个,结合频率的意义可直接求得;(2)由概率与频率的关系可估计从袋中任意摸出一个球,恰好是红球的概率,从而引进未知数,构造方程求解.
解:(1)∵=,
∴参加一次这种游戏活动得到福娃玩具的频率为
典例精析
(2)∵试验次数很大时,频率接近于理论概率,
∴估计从袋中任意摸出一个球,恰好是红球的概率是.
设袋中白球有 x 个.
根据题意,得x+=,
解得x=18,
经检验,x=18是原分式方程的解,且符合题意,
∴估计袋中白球有18个.
课堂练习
1.不透明的袋子里放有4个黑球和若干个白球(这些球除颜色外都相同),老师将全班学生分成10个小组,进行摸球试验,经过大量重复摸球试验,统计显示,从中摸出白球的频率稳定在0.2附近,则袋子中白球的个数是 ( )
A.1 B.2 C.3 D.4
2.甲、乙两名同学在一次用频率估计概率的试验中统计了某一结果出现的频率,绘出的统计图如图所示,则符合这一结果的试验可能是 ( )
A.掷一枚正六面体的骰子,出现1点的概率
B.任意写一个整数,它能被2整除的概率
C.抛一枚质地均匀的硬币,出现正面朝上的概率
D.从一个装有2个白球和1个红球的袋子中任取1个球,取到红球的概率
A
D
课堂练习
3.下表记录了某种幼树在一定条件下移植成活的情况:
移植总数n 400 1500 3500 7000 9000 14000
成活数m 325 1336 3203 6335 8073 12628
成活的频率(精确到0.01) 0.813 0.891 0.915 0.905 0.897 0.902
由此估计这种幼树在此条件下移植成活的概率是_____(精确到0.1).
0.9
课堂练习
(1)请估计:当n很大时,摸到白球的频率将会接近 (精确到0.1);
(2)假如你摸一次,估计你摸到白球的概率P(白球)= .
0.6
0.6
摸球的次数n 100 200 300 500 800 1000 3000
摸到白球次数m 65 124 178 302 481 599 1803
摸到白球概率 0.65 0.62 0.593 0.604 0.601 0.599 0.601
4.在一个不透明的盒子里装有除颜色不同其余均相同的黑、白两种球,其中白球24个,黑球若干.小兵将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是试验中的一组统计数据:
课堂练习
5.某池塘里养了鱼苗10万条,根据这几年的经验知道,鱼苗成活率为95%,一段时间准备打捞出售,第一网捞出40条,称得平均每条鱼重 2.5千克,第二网捞出25条,称得平均每条鱼重2.2千克,第三网捞出35条,称得平均每条鱼重2.8千克,试估计这池塘中鱼的重量.
解:先计算每条鱼的平均重量是:
(2.5×40+2.2×25+2.8×35)÷(40+25+35)=2.53(千克);
所以这池塘中鱼的重量是2.53×100000× 95%=240350(千克).
课堂总结
频率估计概率
大量重复试验
求非等可能性事件概率
列举法
不能适应
频率稳定
常数附近
统计思想
用样本(频率)估计总体(概率)
一种关系
频率与概率的关系
频率稳定时可看作是概
率但概率与频率无关
板书设计
课题:3.2用频率估计概率
当试验次数很多或试验时样本容量足够大时,一件事件发生的频率与相应的概率会非常接近.此时,我们可以用一件事件发生的频率来估计这一事件发生的概率.
作业布置
课本P71 习题3.4 第1,2题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
