北师大版八年级上册数学 1.1.1探索勾股定理 课件(共15张PPT)
文档属性
| 名称 | 北师大版八年级上册数学 1.1.1探索勾股定理 课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 988.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-20 00:00:00 | ||
图片预览



文档简介
(共15张PPT)
预 习
第1课时
探索勾股定理
互 动
展示
生成
检测
预 习
互 动
展示
生成
检测
学习目标
掌握勾股定理,了解利用拼图 验证勾股定理的方法.
(2)已知直角三角形两边的长,会利用勾股定理求第三边.
预 习
互 动
展示
生成
检测
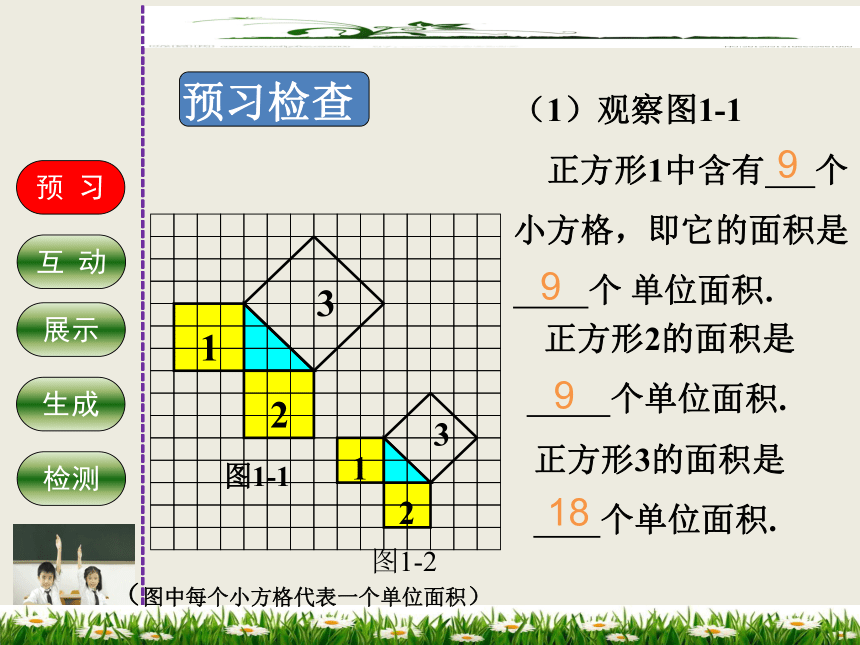
预习检查
1
2
3
1
2
3
(图中每个小方格代表一个单位面积)
图1-1
图1-2
(1)观察图1-1
正方形1中含有 个
小方格,即它的面积是
个 单位面积.
正方形2的面积是
个单位面积.
正方形3的面积是
个单位面积.
9
9
9
18
预 习
互 动
展示
生成
检测
1
2
3
1
2
3
(图中每个小方格代表一个单位面积)
图1-1
图1-2
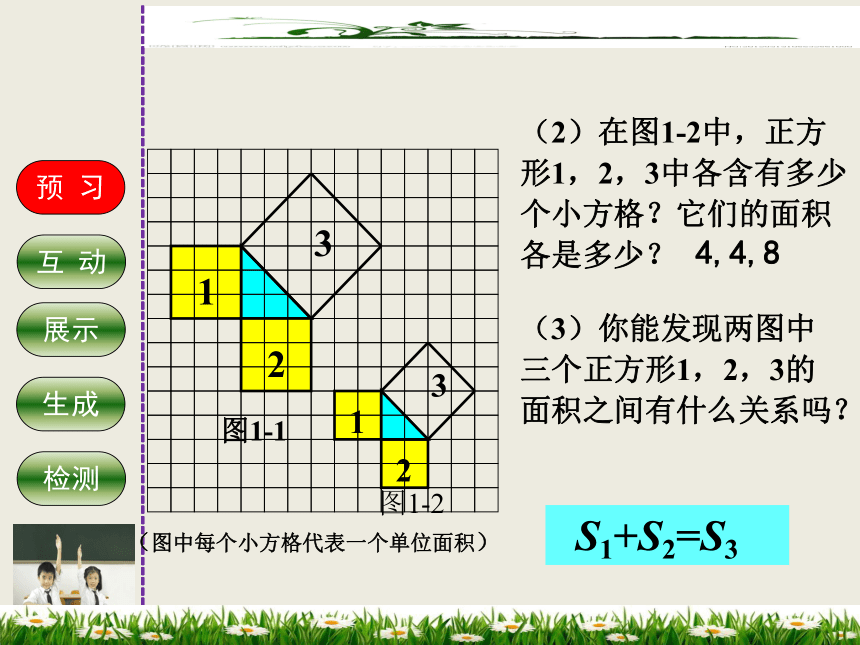
(2)在图1-2中,正方形1,2,3中各含有多少个小方格?它们的面积各是多少?
(3)你能发现两图中三个正方形1,2,3的面积之间有什么关系吗?
S1+S2=S3
4,4,8
预 习
互 动
展示
生成
检测
2
1
3
图2-3
(图中每个小方格代表一个单位面积)
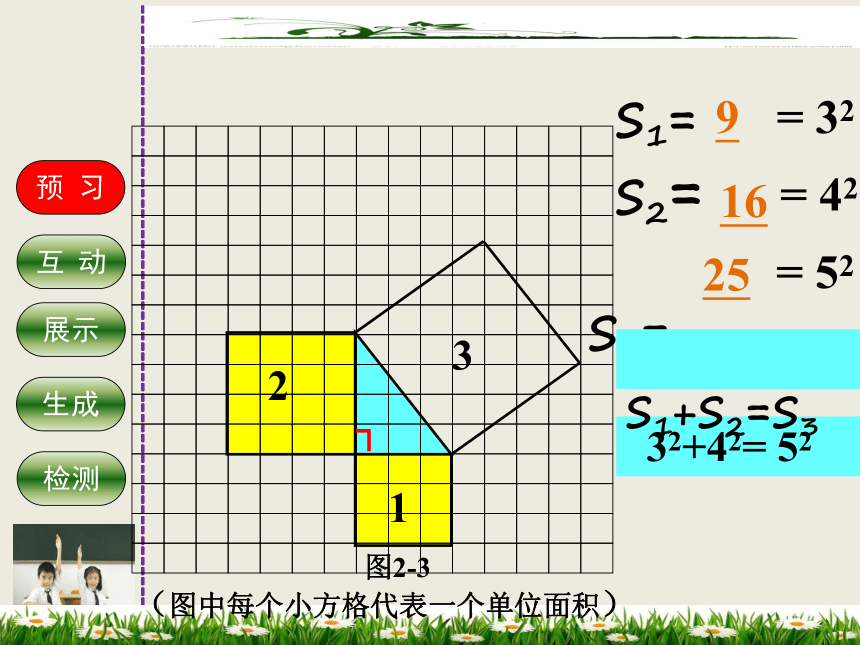
S1=
S2=
S3=
32+42= 52
9
16
25
= 32
= 42
= 52
S1+S2=S3
预 习
互 动
展示
生成
检测
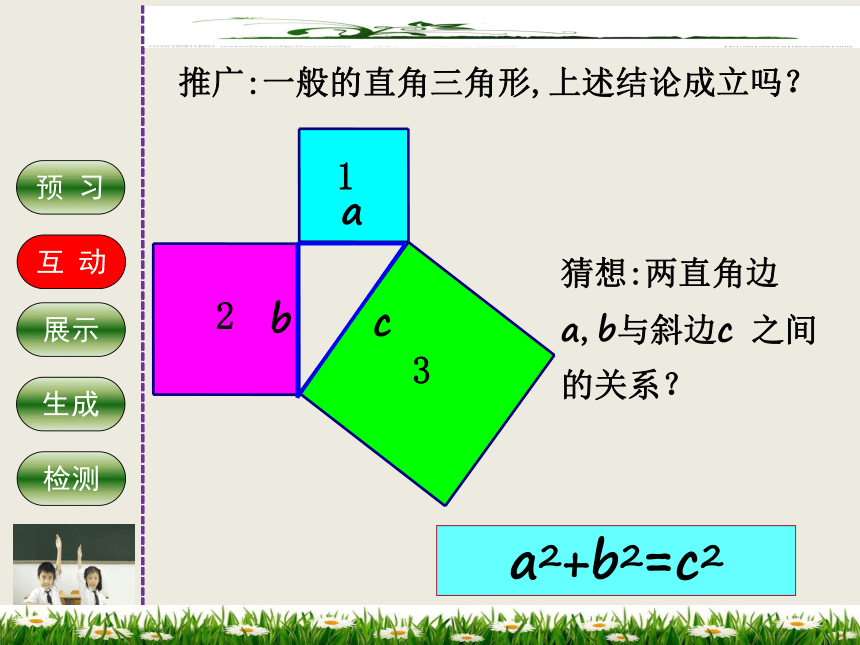
推广:一般的直角三角形,上述结论成立吗?
猜想:两直角边a,b与斜边c 之间的关系?
a2+b2=c2
1
2
3
a
c
b
预 习
互 动
展示
生成
检测
讨论交流,合作探究
1.核心讨论内容:预习或导学案中遇到的疑问和错误
2.问题引领:
(1)勾股定理的内容?探究一
(2)如何验证勾股定理。探究二
(3)如何利用勾股定理进行计算?例1、例2
精彩展示
展示问题 展示小组
探究一
(知识探究部分) 4组(一人)
探究二
(知识探究部分) 5组(一人)
例1、例2 6组(两人)
目标:
(1)书写认真规范,多人快速展示,用白色粉笔写过程彩色粉笔写总结;不超过5分钟
(2)不但要展示解题过程,更重要的是展示规律方法、注意问题的拓展;不浪费一分钟;
(3)小组长要检查落实,力争全部达标
预 习
互 动
展示
生成
检测
预 习
互 动
展示
生成
检测
展示问题 展示小组 点评小组
探究一 4组(一人) 1组
探究二 5组(一人) 2组
例1、例2 6组(两人) 3组
目标:
首先点评思路方法,然后顺着思路方法分析过程,总结规律方法、易错点。
其它同学认真倾听、积极思考,重点内容记好笔记。有不明白或有补充的要大胆提出,学会分享。
(3)力争全部达成目标,注意多拓展、质疑,注重总结,并整理落实。
精彩点评,快乐质疑
预 习
互 动
展示
生成
检测
例 如果直角三角形两直角边长分别为 BC=5厘米 , AC=12厘米,求斜边AB的长度.
解:在Rt△ABC中根据勾股定理,
AC +BC =AB ,
a
b
c
A
C
B
预 习
互 动
展示
生成
检测
勾股定理
如果直角三角形两直角边分别为a,b,斜边为c,那么
直角三角形两直角边的平方和等于斜边的平方
a
b
c
a2+b2=c2
几何语言:
∵ ABC是直角三角形且∠C=90°
∴a2+b2=c2
一、判断题. 1.△ABC的两边AB=5,AC=12,则BC=13 ( ) 2.△ABC的a=6,b=8,则c=10 ( ) 二、填空题 3.在△ABC中, ∠C=90°,AC=6,CB=8,则
△ABC面积为_____,斜边为上的高为______.
24
4.8
A
B
C
D
预 习
互 动
展示
生成
检测
预 习
互 动
展示
生成
检测
4.阴影部分是一个正方形,则此正方形的面积
为 .
15 cm
17 cm
64 cm
巩固提升
预 习
互 动
展示
生成
检测
25或7
5、已知:Rt△ABC中,AB=4,AC=3,则BC2的长为____________
4
3
A
C
B
4
3
C
A
B
应用勾股定理时,必须先判断是直角三角形,然后确定那条是直角边,那条是斜边.
预 习
第1课时
探索勾股定理
互 动
展示
生成
检测
预 习
互 动
展示
生成
检测
学习目标
掌握勾股定理,了解利用拼图 验证勾股定理的方法.
(2)已知直角三角形两边的长,会利用勾股定理求第三边.
预 习
互 动
展示
生成
检测
预习检查
1
2
3
1
2
3
(图中每个小方格代表一个单位面积)
图1-1
图1-2
(1)观察图1-1
正方形1中含有 个
小方格,即它的面积是
个 单位面积.
正方形2的面积是
个单位面积.
正方形3的面积是
个单位面积.
9
9
9
18
预 习
互 动
展示
生成
检测
1
2
3
1
2
3
(图中每个小方格代表一个单位面积)
图1-1
图1-2
(2)在图1-2中,正方形1,2,3中各含有多少个小方格?它们的面积各是多少?
(3)你能发现两图中三个正方形1,2,3的面积之间有什么关系吗?
S1+S2=S3
4,4,8
预 习
互 动
展示
生成
检测
2
1
3
图2-3
(图中每个小方格代表一个单位面积)
S1=
S2=
S3=
32+42= 52
9
16
25
= 32
= 42
= 52
S1+S2=S3
预 习
互 动
展示
生成
检测
推广:一般的直角三角形,上述结论成立吗?
猜想:两直角边a,b与斜边c 之间的关系?
a2+b2=c2
1
2
3
a
c
b
预 习
互 动
展示
生成
检测
讨论交流,合作探究
1.核心讨论内容:预习或导学案中遇到的疑问和错误
2.问题引领:
(1)勾股定理的内容?探究一
(2)如何验证勾股定理。探究二
(3)如何利用勾股定理进行计算?例1、例2
精彩展示
展示问题 展示小组
探究一
(知识探究部分) 4组(一人)
探究二
(知识探究部分) 5组(一人)
例1、例2 6组(两人)
目标:
(1)书写认真规范,多人快速展示,用白色粉笔写过程彩色粉笔写总结;不超过5分钟
(2)不但要展示解题过程,更重要的是展示规律方法、注意问题的拓展;不浪费一分钟;
(3)小组长要检查落实,力争全部达标
预 习
互 动
展示
生成
检测
预 习
互 动
展示
生成
检测
展示问题 展示小组 点评小组
探究一 4组(一人) 1组
探究二 5组(一人) 2组
例1、例2 6组(两人) 3组
目标:
首先点评思路方法,然后顺着思路方法分析过程,总结规律方法、易错点。
其它同学认真倾听、积极思考,重点内容记好笔记。有不明白或有补充的要大胆提出,学会分享。
(3)力争全部达成目标,注意多拓展、质疑,注重总结,并整理落实。
精彩点评,快乐质疑
预 习
互 动
展示
生成
检测
例 如果直角三角形两直角边长分别为 BC=5厘米 , AC=12厘米,求斜边AB的长度.
解:在Rt△ABC中根据勾股定理,
AC +BC =AB ,
a
b
c
A
C
B
预 习
互 动
展示
生成
检测
勾股定理
如果直角三角形两直角边分别为a,b,斜边为c,那么
直角三角形两直角边的平方和等于斜边的平方
a
b
c
a2+b2=c2
几何语言:
∵ ABC是直角三角形且∠C=90°
∴a2+b2=c2
一、判断题. 1.△ABC的两边AB=5,AC=12,则BC=13 ( ) 2.△ABC的a=6,b=8,则c=10 ( ) 二、填空题 3.在△ABC中, ∠C=90°,AC=6,CB=8,则
△ABC面积为_____,斜边为上的高为______.
24
4.8
A
B
C
D
预 习
互 动
展示
生成
检测
预 习
互 动
展示
生成
检测
4.阴影部分是一个正方形,则此正方形的面积
为 .
15 cm
17 cm
64 cm
巩固提升
预 习
互 动
展示
生成
检测
25或7
5、已知:Rt△ABC中,AB=4,AC=3,则BC2的长为____________
4
3
A
C
B
4
3
C
A
B
应用勾股定理时,必须先判断是直角三角形,然后确定那条是直角边,那条是斜边.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
