北师大版八年级上册数学 1.2一定是直角三角形吗 课件(共14张PPT)
文档属性
| 名称 | 北师大版八年级上册数学 1.2一定是直角三角形吗 课件(共14张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 375.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-20 09:34:29 | ||
图片预览






文档简介
(共14张PPT)
1.2一定是直角三角形吗
-----勾股定理的逆定理
1,勾股定理的内容是什么 用字母如何表示
直角三角形两直角边a、b的平方和等于斜边c的平方.
∠C=90° a2+b2=c2
2,如果这个定理的条件和结论互换,那么它还成立吗
即:一个三角形的三边满足a2+b2=c2,那么这个三角形是直角三角形吗
a2+b2=c2 ∠C=90°°
回顾与思考
1.2一定是直角三角形吗
1. 大约公元前2700年间,古埃及人建成了世界闻名的金字塔.
2. 问题:古埃及人是怎样画直角,从而画出正方形的呢
引入新课
1、画图:画出边长分别是下列各组数的三角形。
A. 3 、4、5 B. 3、4、3
C. 3、4、6 D. 5、12、13
请判断一下上述你所画的三角形的形状。
A:— B:— C:— D:—
1、找规律:
(3,4,5)→两条短边的平方和 __ 最长边的平方
(3,4,3)→两条短边的平方和 __ 最长边的平方
(3,4,6)→两条短边的平方和 __ 最长边的平方
2、猜一猜 :
一个三角形的两条短边的平方和与最长边的平方满足怎样的关系时,这个三角形才可能是直角三角形呢?
你的猜想是:
如果三角形的三边长a,b,c满足a2 +b2=c2 ,
那么这个三角形是直角三角形
等于
小于
大于
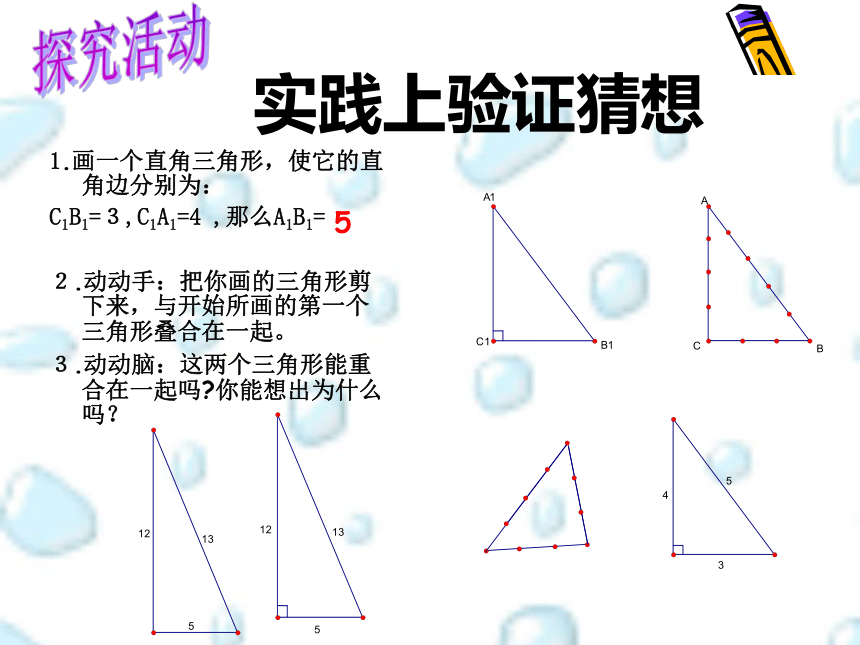
实践上验证猜想
1.画一个直角三角形,使它的直角边分别为:
C1B1=3,C1A1=4 ,那么A1B1=
2.动动手:把你画的三角形剪下来,与开始所画的第一个三角形叠合在一起。
3.动动脑:这两个三角形能重合在一起吗 你能想出为什么吗?
5
已知:在⊿ABC中,AB=c,BC=a,CA=b,并且a2+b2=c2,求证:∠C=90°
证明:作⊿A1B1C1,使∠C1=90°,B1C1=a,C1A1=b,
那么(A1B1)2=a2+b2
∵a2+b2=c2
∴A1B1=c (A1B1>0)
在⊿ ABC和⊿A1B1C1中,
BC=B1C1
CA=C1A1
AB=A1B1
∴⊿ABC≌⊿A1B1C1
∴∠C=90°
理论上验证猜想
1.通过以上的验证:你们的猜想是否正确?你能再叙述一下这个猜想吗?
如果三角形的三边长a,b,c满足a2 +b2=c2 ,
那么这个三角形是直角三角形
a2+b2=c2 ∠C=90°
2.上述猜想与勾股定理有什么区别和联系?
∠C=90° a2+b2=c2
3.你能给上面的猜想起个名字吗?
勾股定理的逆定理
结论:勾股定理的逆定理
勾股数:满足a2+b2=c2的三个正整数,称为勾股数。
如果三角形的三边长a,b,c满足a2 +b2=c2 ,
那么这个三角形是直角三角形
1.下列几组数能否作为直角三 角形的三边长 说说你的理由
(1)9,12,15
(2)4, 5, 6
(3)0.3 ,0.4,0.5
(4)12,18,22
2.如图,在正方形ABCD中,AB=4,AE=2,DF=1,图中有几个直角三角形,你是如何判断的?与同伴交流.
(能∵ 92+122=152)
(不能∵42+52≠62)
(能∵0.32+0.42=0.52)
(不能∵122+182≠222)
例1 一个零件的形状如图所示,按规定这个零件中∠A和∠DBC都应为直角。工人师傅量得这个零件各边长尺寸如图所AB=3,AD=4, DB=5,BC=12,DC=13,这个零件符合要求吗?
解:在⊿ABD中,
∵32+42=52
即 AB2+AD2=BD2
∴∠A=90°
在⊿BDC中,
∵52+122=132
即 BD2+BC2=DC2
∴∠DBC=90°
因此这个零件符合要求.
y=0
应用知识回归生活
2.古埃及人曾用下面的方法得到直角:如图所示,他们用13个等距的结把一根绳子分成等长的12段,一个工匠同时握着绳子的第1个结和第13个结,两个助手分别握着第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其直角在第4个结处.
y=0
应用知识回归生活
勾股定理的逆定理和勾股数.
直角三角形的判别方法.
你还有什么问题吗?
1.P10 2、3
2.探索勾股数:a=2mn,b=n2-m2,c=n2+m2,m、n是正整数,m、n一奇一偶,且互质,n﹥m,问:a,b,c可以作为勾股数吗?
1.2一定是直角三角形吗
-----勾股定理的逆定理
1,勾股定理的内容是什么 用字母如何表示
直角三角形两直角边a、b的平方和等于斜边c的平方.
∠C=90° a2+b2=c2
2,如果这个定理的条件和结论互换,那么它还成立吗
即:一个三角形的三边满足a2+b2=c2,那么这个三角形是直角三角形吗
a2+b2=c2 ∠C=90°°
回顾与思考
1.2一定是直角三角形吗
1. 大约公元前2700年间,古埃及人建成了世界闻名的金字塔.
2. 问题:古埃及人是怎样画直角,从而画出正方形的呢
引入新课
1、画图:画出边长分别是下列各组数的三角形。
A. 3 、4、5 B. 3、4、3
C. 3、4、6 D. 5、12、13
请判断一下上述你所画的三角形的形状。
A:— B:— C:— D:—
1、找规律:
(3,4,5)→两条短边的平方和 __ 最长边的平方
(3,4,3)→两条短边的平方和 __ 最长边的平方
(3,4,6)→两条短边的平方和 __ 最长边的平方
2、猜一猜 :
一个三角形的两条短边的平方和与最长边的平方满足怎样的关系时,这个三角形才可能是直角三角形呢?
你的猜想是:
如果三角形的三边长a,b,c满足a2 +b2=c2 ,
那么这个三角形是直角三角形
等于
小于
大于
实践上验证猜想
1.画一个直角三角形,使它的直角边分别为:
C1B1=3,C1A1=4 ,那么A1B1=
2.动动手:把你画的三角形剪下来,与开始所画的第一个三角形叠合在一起。
3.动动脑:这两个三角形能重合在一起吗 你能想出为什么吗?
5
已知:在⊿ABC中,AB=c,BC=a,CA=b,并且a2+b2=c2,求证:∠C=90°
证明:作⊿A1B1C1,使∠C1=90°,B1C1=a,C1A1=b,
那么(A1B1)2=a2+b2
∵a2+b2=c2
∴A1B1=c (A1B1>0)
在⊿ ABC和⊿A1B1C1中,
BC=B1C1
CA=C1A1
AB=A1B1
∴⊿ABC≌⊿A1B1C1
∴∠C=90°
理论上验证猜想
1.通过以上的验证:你们的猜想是否正确?你能再叙述一下这个猜想吗?
如果三角形的三边长a,b,c满足a2 +b2=c2 ,
那么这个三角形是直角三角形
a2+b2=c2 ∠C=90°
2.上述猜想与勾股定理有什么区别和联系?
∠C=90° a2+b2=c2
3.你能给上面的猜想起个名字吗?
勾股定理的逆定理
结论:勾股定理的逆定理
勾股数:满足a2+b2=c2的三个正整数,称为勾股数。
如果三角形的三边长a,b,c满足a2 +b2=c2 ,
那么这个三角形是直角三角形
1.下列几组数能否作为直角三 角形的三边长 说说你的理由
(1)9,12,15
(2)4, 5, 6
(3)0.3 ,0.4,0.5
(4)12,18,22
2.如图,在正方形ABCD中,AB=4,AE=2,DF=1,图中有几个直角三角形,你是如何判断的?与同伴交流.
(能∵ 92+122=152)
(不能∵42+52≠62)
(能∵0.32+0.42=0.52)
(不能∵122+182≠222)
例1 一个零件的形状如图所示,按规定这个零件中∠A和∠DBC都应为直角。工人师傅量得这个零件各边长尺寸如图所AB=3,AD=4, DB=5,BC=12,DC=13,这个零件符合要求吗?
解:在⊿ABD中,
∵32+42=52
即 AB2+AD2=BD2
∴∠A=90°
在⊿BDC中,
∵52+122=132
即 BD2+BC2=DC2
∴∠DBC=90°
因此这个零件符合要求.
y=0
应用知识回归生活
2.古埃及人曾用下面的方法得到直角:如图所示,他们用13个等距的结把一根绳子分成等长的12段,一个工匠同时握着绳子的第1个结和第13个结,两个助手分别握着第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其直角在第4个结处.
y=0
应用知识回归生活
勾股定理的逆定理和勾股数.
直角三角形的判别方法.
你还有什么问题吗?
1.P10 2、3
2.探索勾股数:a=2mn,b=n2-m2,c=n2+m2,m、n是正整数,m、n一奇一偶,且互质,n﹥m,问:a,b,c可以作为勾股数吗?
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
