北师大版八年级上册数学 1.4勾股定理 回顾与思考 课件(共20张PPT)
文档属性
| 名称 | 北师大版八年级上册数学 1.4勾股定理 回顾与思考 课件(共20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-20 09:43:35 | ||
图片预览




文档简介
(共20张PPT)
华罗庚
《勾股定理》复习课
八年级数学(上册) 北师大版
直角三角形两直角边的平方和等于斜边的平方.如果两直角边分别为a,b,斜边为c,那么
a2=c2-b2
b2 =c2-a2
a2+b2=c2
c
b
a
C
B
A
勾股定理
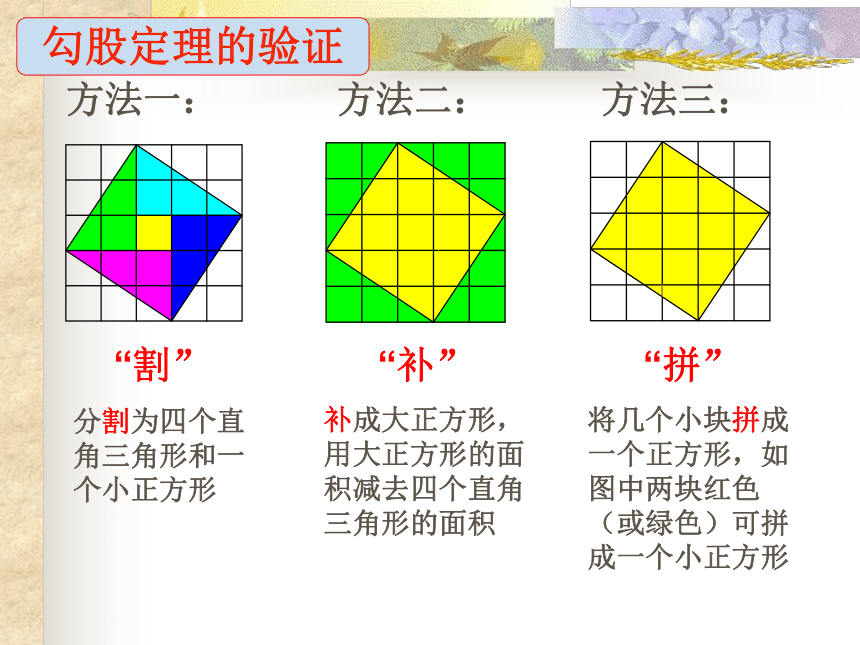
“补”
“拼”
“割”
方法一:
方法二:
方法三:
分割为四个直角三角形和一个小正方形
补成大正方形,用大正方形的面积减去四个直角三角形的面积
将几个小块拼成一个正方形,如图中两块红色(或绿色)可拼成一个小正方形
勾股定理的验证
一、三国时期数学家赵爽在为《周髀算经》作注时,创制了一幅“勾股圆方图”,也称为“弦图”,这是我国对勾股定理最早的证明.它用几何图形来证明代数式之间的恒等关系,体现了以形证数、形数统一、代数和几何的紧密结合 .
由面积计算,得
展开,得
化简,得
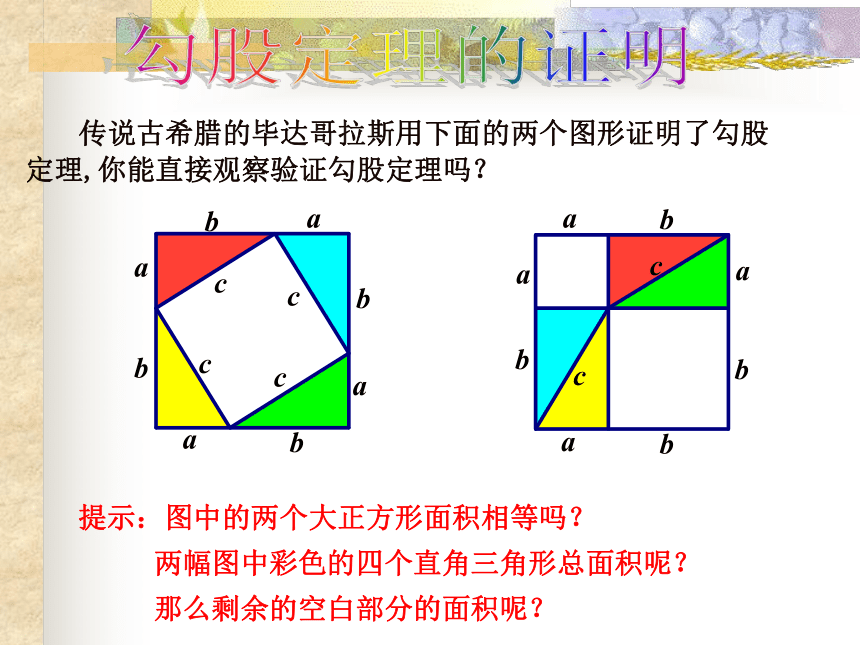
传说古希腊的毕达哥拉斯用下面的两个图形证明了勾股定理,你能直接观察验证勾股定理吗?
两幅图中彩色的四个直角三角形总面积呢?
提示:图中的两个大正方形面积相等吗?
那么剩余的空白部分的面积呢?
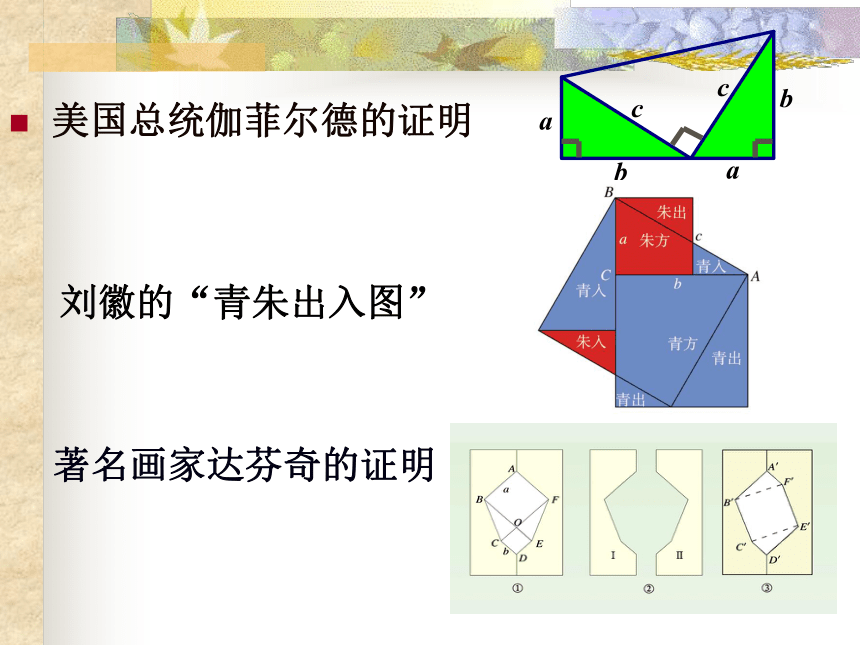
美国总统伽菲尔德的证明
刘徽的“青朱出入图”
著名画家达芬奇的证明
1
1
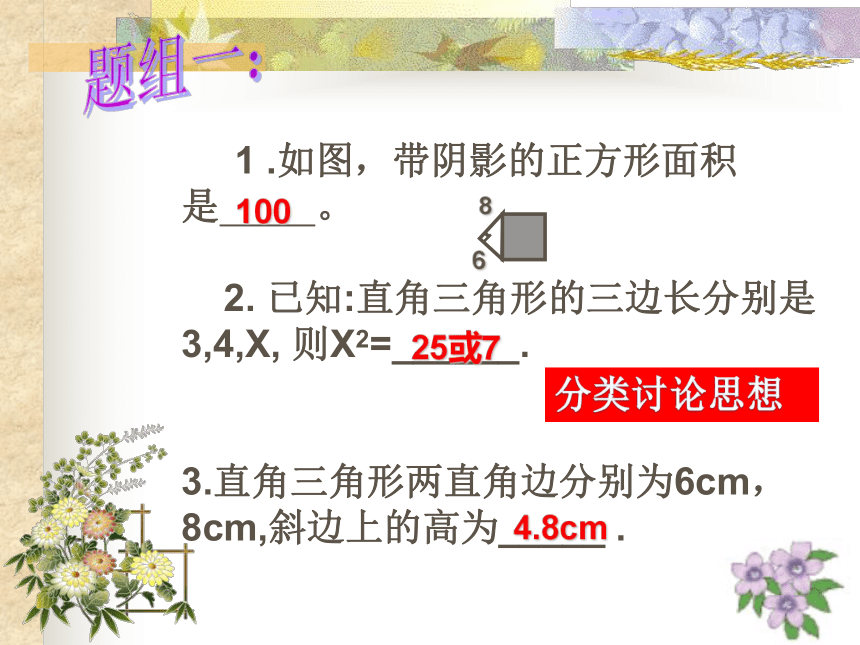
1 .如图,带阴影的正方形面积是 。
2. 已知:直角三角形的三边长分别是 3,4,X, 则X2=______.
3.直角三角形两直角边分别为6cm,8cm,斜边上的高为_____ .
100
25或7
4.8cm
8
6
如果三角形的三边长a,b,c满足a2 +b2=c2 ,那么这个三角形是直角三角形.
满足a2 +b2=c2的三个正整数,称为勾股数.
3、 4、 5; 6、8、10; 9、12、15.
5、12、13; 7、24、25; 9、40、41.
8、15、17; 10、24、26;12、35、37.
直角三角形的判别条件
若a2 +b2>c2, 则是锐角三角形。
若a2 +b2<c2 ,则是 钝角三角形。
1、满足下列条件的三角形是不是直角三角形
(1)三边满足 a:b:c=3:4:5
(2)三边满足(a+b)2=2ab+c2
(3) ∠A: ∠B: ∠C=1:5:6
2、下面是勾股数的一组是( )
A 6,8,10 B -6,-8 ,-10
C , , D 0.3 ,0.4, 0.5
是
是
是
A
数学思想方法是解决数学问题的灵魂.正解的运用数学思想方法也是成功解题的关键.尤其是在运用勾股定理解题时,更应注重思想方法的运用。
实际应用
(2016 哈尔滨改编)甲、乙两船从港口A同时出发,甲船以30海里/小时的速度向北偏东35°的方向航行,乙船以40海里/小时的速度另一个方向航行,2小时后,甲船达到C岛,乙船到达B岛。若两岛相距100海里,问:乙船航行的方向是南偏东多少度?
A
B
C
35°
⌒
(2014年安徽省)如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( )
A. B. C.4 D.5
(2015 资阳)如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是
( )
A.13cm B. 2 cm C. cm D. 2 cm
3、学习过程中你还有什么困惑?
感悟与收获
1、通过这节课的学习活动你有哪些收获?
2、通过本节课的学习,你获得了那些数学思想和方法?
必做题 :
1、课本第16页复习题
3,4,5 B组1
2、独立完成一份小结,用自己的语言梳理本章的内容。
选做题:
勾股定理不仅在数学的发展中起着重要作用,而且在现实世界中有着广泛应用,请同学们试举几例,感受数学与生活的紧密相连。
思考题:
如图所示,已知等腰三角形ABC的底边BC=20cm,D是腰AB上一点,且CD=16cm,BD=12cm,求△ABC的周长.
结束寄语
数学使人聪明,数学使人陶醉,数学的美陶冶着你、我、他.
再见!
华罗庚
《勾股定理》复习课
八年级数学(上册) 北师大版
直角三角形两直角边的平方和等于斜边的平方.如果两直角边分别为a,b,斜边为c,那么
a2=c2-b2
b2 =c2-a2
a2+b2=c2
c
b
a
C
B
A
勾股定理
“补”
“拼”
“割”
方法一:
方法二:
方法三:
分割为四个直角三角形和一个小正方形
补成大正方形,用大正方形的面积减去四个直角三角形的面积
将几个小块拼成一个正方形,如图中两块红色(或绿色)可拼成一个小正方形
勾股定理的验证
一、三国时期数学家赵爽在为《周髀算经》作注时,创制了一幅“勾股圆方图”,也称为“弦图”,这是我国对勾股定理最早的证明.它用几何图形来证明代数式之间的恒等关系,体现了以形证数、形数统一、代数和几何的紧密结合 .
由面积计算,得
展开,得
化简,得
传说古希腊的毕达哥拉斯用下面的两个图形证明了勾股定理,你能直接观察验证勾股定理吗?
两幅图中彩色的四个直角三角形总面积呢?
提示:图中的两个大正方形面积相等吗?
那么剩余的空白部分的面积呢?
美国总统伽菲尔德的证明
刘徽的“青朱出入图”
著名画家达芬奇的证明
1
1
1 .如图,带阴影的正方形面积是 。
2. 已知:直角三角形的三边长分别是 3,4,X, 则X2=______.
3.直角三角形两直角边分别为6cm,8cm,斜边上的高为_____ .
100
25或7
4.8cm
8
6
如果三角形的三边长a,b,c满足a2 +b2=c2 ,那么这个三角形是直角三角形.
满足a2 +b2=c2的三个正整数,称为勾股数.
3、 4、 5; 6、8、10; 9、12、15.
5、12、13; 7、24、25; 9、40、41.
8、15、17; 10、24、26;12、35、37.
直角三角形的判别条件
若a2 +b2>c2, 则是锐角三角形。
若a2 +b2<c2 ,则是 钝角三角形。
1、满足下列条件的三角形是不是直角三角形
(1)三边满足 a:b:c=3:4:5
(2)三边满足(a+b)2=2ab+c2
(3) ∠A: ∠B: ∠C=1:5:6
2、下面是勾股数的一组是( )
A 6,8,10 B -6,-8 ,-10
C , , D 0.3 ,0.4, 0.5
是
是
是
A
数学思想方法是解决数学问题的灵魂.正解的运用数学思想方法也是成功解题的关键.尤其是在运用勾股定理解题时,更应注重思想方法的运用。
实际应用
(2016 哈尔滨改编)甲、乙两船从港口A同时出发,甲船以30海里/小时的速度向北偏东35°的方向航行,乙船以40海里/小时的速度另一个方向航行,2小时后,甲船达到C岛,乙船到达B岛。若两岛相距100海里,问:乙船航行的方向是南偏东多少度?
A
B
C
35°
⌒
(2014年安徽省)如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( )
A. B. C.4 D.5
(2015 资阳)如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是
( )
A.13cm B. 2 cm C. cm D. 2 cm
3、学习过程中你还有什么困惑?
感悟与收获
1、通过这节课的学习活动你有哪些收获?
2、通过本节课的学习,你获得了那些数学思想和方法?
必做题 :
1、课本第16页复习题
3,4,5 B组1
2、独立完成一份小结,用自己的语言梳理本章的内容。
选做题:
勾股定理不仅在数学的发展中起着重要作用,而且在现实世界中有着广泛应用,请同学们试举几例,感受数学与生活的紧密相连。
思考题:
如图所示,已知等腰三角形ABC的底边BC=20cm,D是腰AB上一点,且CD=16cm,BD=12cm,求△ABC的周长.
结束寄语
数学使人聪明,数学使人陶醉,数学的美陶冶着你、我、他.
再见!
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
