14.3.1等腰三角形的性质[上学期]
文档属性
| 名称 | 14.3.1等腰三角形的性质[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 170.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-30 10:01:00 | ||
图片预览



文档简介
课件19张PPT。 1、掌握等腰三角形性质定理和这个定理的两个
推论。目标2、理解等腰三角形性质定理的证明过程,并探
索辅助线的规律。3、初步学会分析几何证明的思路,从而提高学
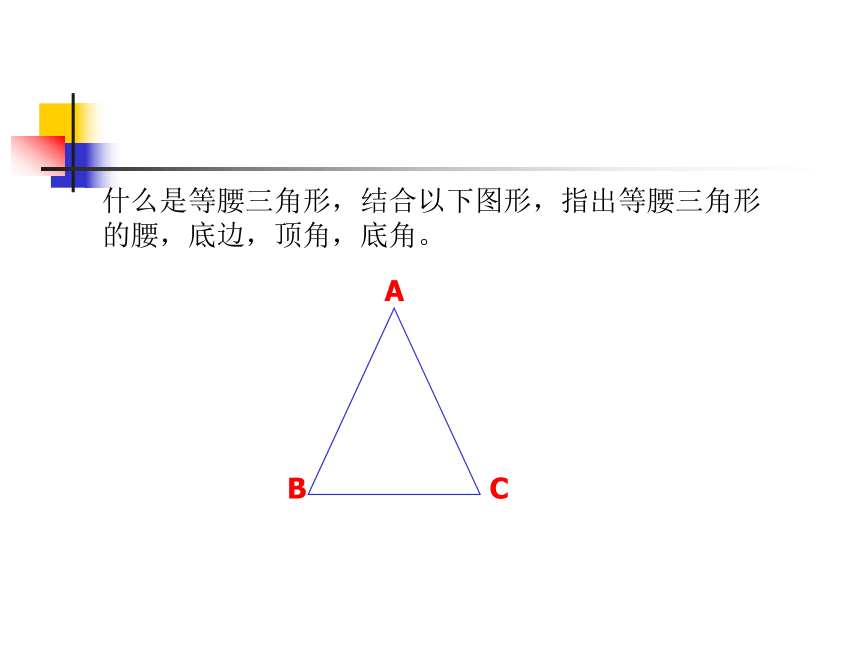
生逻辑能力及分析问题,解决问题的能力。等腰三角形的性质下面这些图形给我们什么印象?什么是等腰三角形,结合以下图形,指出等腰三角形
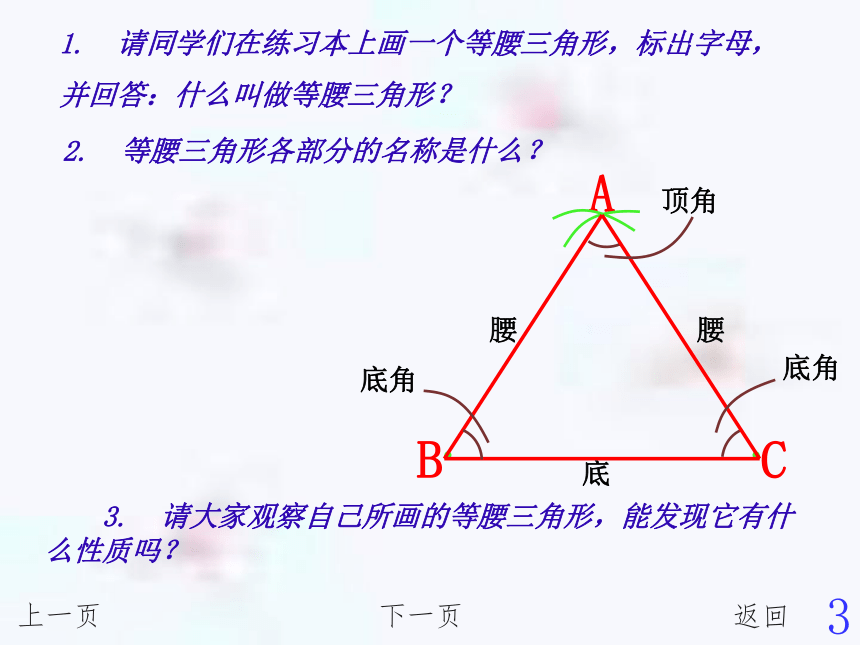
的腰,底边,顶角,底角。ABC1. 请同学们在练习本上画一个等腰三角形,标出字母,
并回答:什么叫做等腰三角形? 3. 请大家观察自己所画的等腰三角形,能发现它有什么性质吗?腰腰底顶角底角
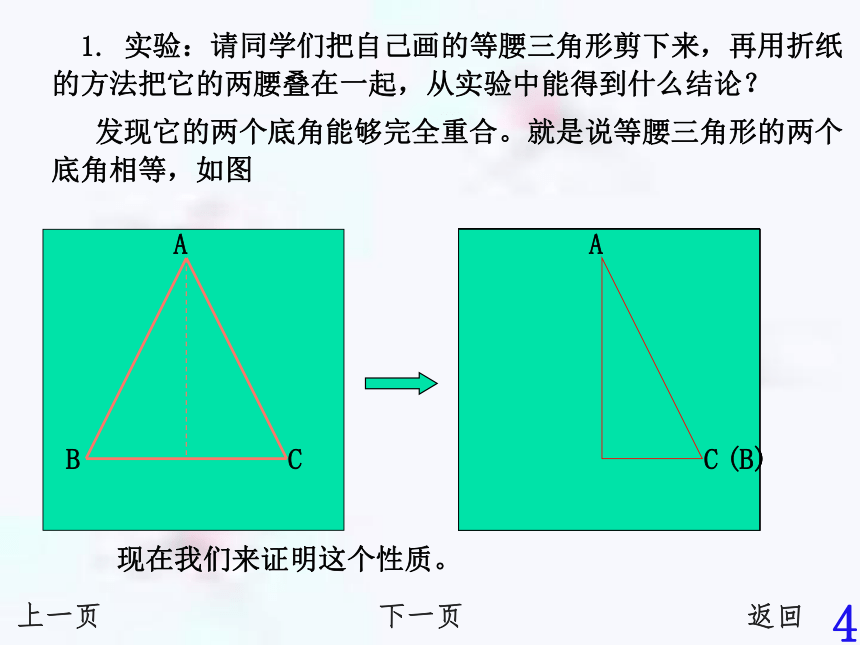
底角2. 等腰三角形各部分的名称是什么?上一页下一页返回ABC3 现在我们来证明这个性质。 1. 实验:请同学们把自己画的等腰三角形剪下来,再用折纸的方法把它的两腰叠在一起,从实验中能得到什么结论?
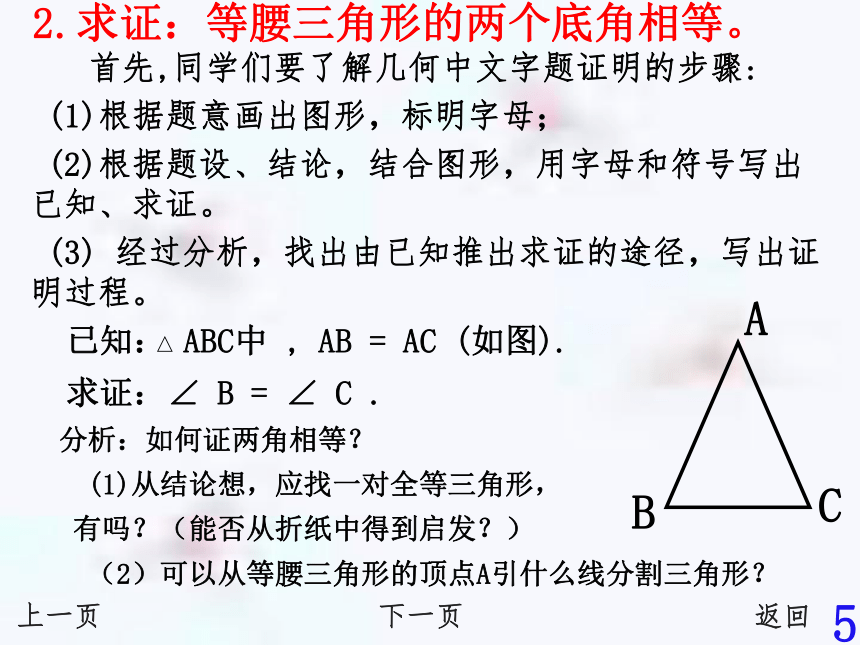
发现它的两个底角能够完全重合。就是说等腰三角形的两个底角相等,如图上一页下一页返回4 首先,同学们要了解几何中文字题证明的步骤:
(1)根据题意画出图形,标明字母;
(2)根据题设、结论,结合图形,用字母和符号写出已知、求证。
(3) 经过分析,找出由已知推出求证的途径,写出证明过程。分析:如何证两角相等?
(1)从结论想,应找一对全等三角形,
有吗?(能否从折纸中得到启发?)
(2)可以从等腰三角形的顶点A引什么线分割三角形?上一页下一页返回2.求证:等腰三角形的两个底角相等。5D12 ①引顶角平分线,可以得到满足“SAS”的一对全等三角形。 ②引中线,可以得到满足“SSS”的一对
全等三角形。
③引高线,可以得到满足“HL”的一对
全等直角三角形。上一页下一页返回等腰三角形的性质定理 等腰三角形的两底角相等。
(简写成“等边对等角”)。 我们选第一种作辅助线法来写出证明过程,后两种留给同学
们课外思考。6D BD = CD, ∠ADB = ∠ADC = 90°, 所以 AD 平分BC, 并且AD⊥BC, 即∴ ∠B = ∠C 上一页下一页返回7等腰三角形的顶角平分线,底边上的中线,底边上的高互相重合。已知:如图房屋的顶角∠BAC=100°,过屋顶A的立柱AD⊥BC,屋椽AB=AC。
求顶架上∠B, ∠C, ∠BAD, ∠CAD的度数。例1: 一、等腰三角形的性质定理:
等腰三角形的两个底角相等
两个推论:
①、等腰三角形顶角的平分线平分底边并且垂直于底边。
②、等边三角形的各角都相等,并且每一个角都等于60°。
二、运用定理和推论解决有关问题。小结 1、怎样从等腰三角形的性质定理得出推论:等腰三角形的每一个锐角都等于45度。
2、如果等腰三角形的一个底角等于75度,那么它的顶角等于多少度?
3、等腰直角三角形的斜边上的高分成两个角,求这两个角的度数?课堂检测 根据等腰三角形性质定理的推论,
在三角形ABC中, AB=AC时,
a ∵ AD⊥BC,
∴ ∠ =∠ , = .
b ∵ AD是中线
∴ ⊥ , ∠ = ∠ .
c ∵ AD是角平分线
∴ ⊥ , = .填空BADCADBDCDBADADBCCADADBCBDCD已知, ABC是等边三角形,AD是高,画出图形,说出图中∠BAD、∠BAC、∠B、∠C的度数。解答题1、 证明等腰三角形的性质定理还有那些
方法?
2 、已知AB=AC,BD⊥AC,求证:
∠DBC = ---∠A12思考题布置作业页: 第 2题
第3题1.口答
(1)怎样从等腰三角形的性质定理得出推论:
等腰直角三角形的每一个锐角都等于 45°?
(2)如果等腰三角形的一个底角等于75°,那么它的顶角等于多少度?
(3)等腰直角三角形斜边上的高把直角分成两个角,求这两个角的度数.上一页下一页返回30°45°、45°60°、30°、60°、60°。10 课外思考题: 2. 直角三角形ABC中, ∠BCA= 90°,AC=AE, BC=BF,
E、F在斜边BA上,求∠ECF的度数. 1. 如图 , B、C、D、E在同一条直线上,
BC=CA=AD=DE,∠CAD = 90°
求: ∠BAE的度数.返回上一页作业: 书上72页 3、4、5。11
推论。目标2、理解等腰三角形性质定理的证明过程,并探
索辅助线的规律。3、初步学会分析几何证明的思路,从而提高学
生逻辑能力及分析问题,解决问题的能力。等腰三角形的性质下面这些图形给我们什么印象?什么是等腰三角形,结合以下图形,指出等腰三角形
的腰,底边,顶角,底角。ABC1. 请同学们在练习本上画一个等腰三角形,标出字母,
并回答:什么叫做等腰三角形? 3. 请大家观察自己所画的等腰三角形,能发现它有什么性质吗?腰腰底顶角底角
底角2. 等腰三角形各部分的名称是什么?上一页下一页返回ABC3 现在我们来证明这个性质。 1. 实验:请同学们把自己画的等腰三角形剪下来,再用折纸的方法把它的两腰叠在一起,从实验中能得到什么结论?
发现它的两个底角能够完全重合。就是说等腰三角形的两个底角相等,如图上一页下一页返回4 首先,同学们要了解几何中文字题证明的步骤:
(1)根据题意画出图形,标明字母;
(2)根据题设、结论,结合图形,用字母和符号写出已知、求证。
(3) 经过分析,找出由已知推出求证的途径,写出证明过程。分析:如何证两角相等?
(1)从结论想,应找一对全等三角形,
有吗?(能否从折纸中得到启发?)
(2)可以从等腰三角形的顶点A引什么线分割三角形?上一页下一页返回2.求证:等腰三角形的两个底角相等。5D12 ①引顶角平分线,可以得到满足“SAS”的一对全等三角形。 ②引中线,可以得到满足“SSS”的一对
全等三角形。
③引高线,可以得到满足“HL”的一对
全等直角三角形。上一页下一页返回等腰三角形的性质定理 等腰三角形的两底角相等。
(简写成“等边对等角”)。 我们选第一种作辅助线法来写出证明过程,后两种留给同学
们课外思考。6D BD = CD, ∠ADB = ∠ADC = 90°, 所以 AD 平分BC, 并且AD⊥BC, 即∴ ∠B = ∠C 上一页下一页返回7等腰三角形的顶角平分线,底边上的中线,底边上的高互相重合。已知:如图房屋的顶角∠BAC=100°,过屋顶A的立柱AD⊥BC,屋椽AB=AC。
求顶架上∠B, ∠C, ∠BAD, ∠CAD的度数。例1: 一、等腰三角形的性质定理:
等腰三角形的两个底角相等
两个推论:
①、等腰三角形顶角的平分线平分底边并且垂直于底边。
②、等边三角形的各角都相等,并且每一个角都等于60°。
二、运用定理和推论解决有关问题。小结 1、怎样从等腰三角形的性质定理得出推论:等腰三角形的每一个锐角都等于45度。
2、如果等腰三角形的一个底角等于75度,那么它的顶角等于多少度?
3、等腰直角三角形的斜边上的高分成两个角,求这两个角的度数?课堂检测 根据等腰三角形性质定理的推论,
在三角形ABC中, AB=AC时,
a ∵ AD⊥BC,
∴ ∠ =∠ , = .
b ∵ AD是中线
∴ ⊥ , ∠ = ∠ .
c ∵ AD是角平分线
∴ ⊥ , = .填空BADCADBDCDBADADBCCADADBCBDCD已知, ABC是等边三角形,AD是高,画出图形,说出图中∠BAD、∠BAC、∠B、∠C的度数。解答题1、 证明等腰三角形的性质定理还有那些
方法?
2 、已知AB=AC,BD⊥AC,求证:
∠DBC = ---∠A12思考题布置作业页: 第 2题
第3题1.口答
(1)怎样从等腰三角形的性质定理得出推论:
等腰直角三角形的每一个锐角都等于 45°?
(2)如果等腰三角形的一个底角等于75°,那么它的顶角等于多少度?
(3)等腰直角三角形斜边上的高把直角分成两个角,求这两个角的度数.上一页下一页返回30°45°、45°60°、30°、60°、60°。10 课外思考题: 2. 直角三角形ABC中, ∠BCA= 90°,AC=AE, BC=BF,
E、F在斜边BA上,求∠ECF的度数. 1. 如图 , B、C、D、E在同一条直线上,
BC=CA=AD=DE,∠CAD = 90°
求: ∠BAE的度数.返回上一页作业: 书上72页 3、4、5。11
