人教版数学八年级上册11.2.1三角形的内角 课件(共49张PPT)
文档属性
| 名称 | 人教版数学八年级上册11.2.1三角形的内角 课件(共49张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-20 10:58:33 | ||
图片预览


文档简介
(共49张PPT)
三角形的内角
(第二课时)
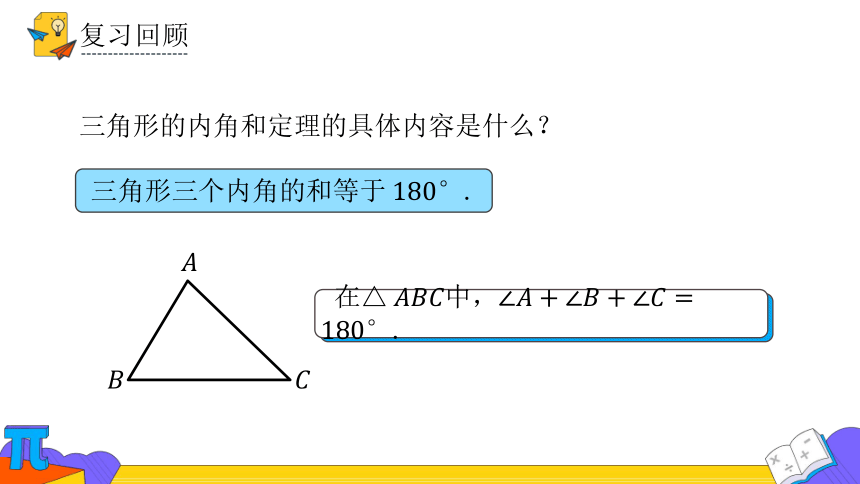
复习回顾
三角形的内角和定理的具体内容是什么?
三角形.
在中,.
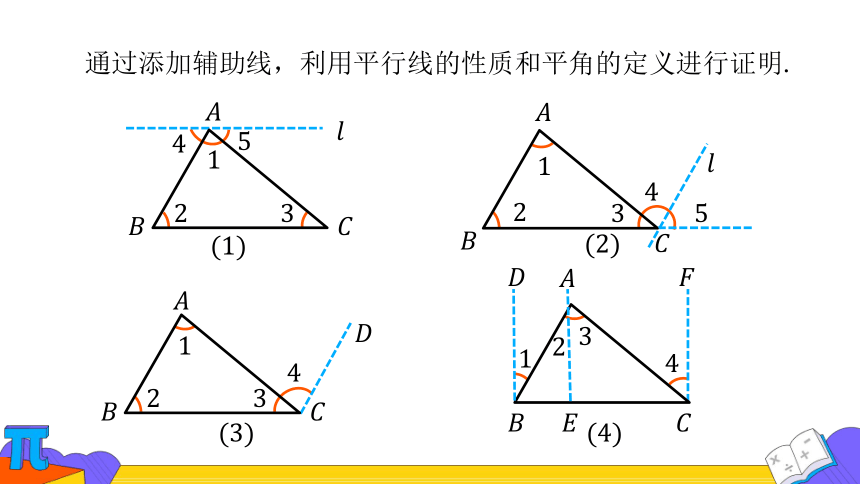
我们在小学的实验基础上,发现了证明三角形内角和定理的方法,你还记得吗?
通过添加辅助线,利用平行线的性质和平角的定义进行证明.
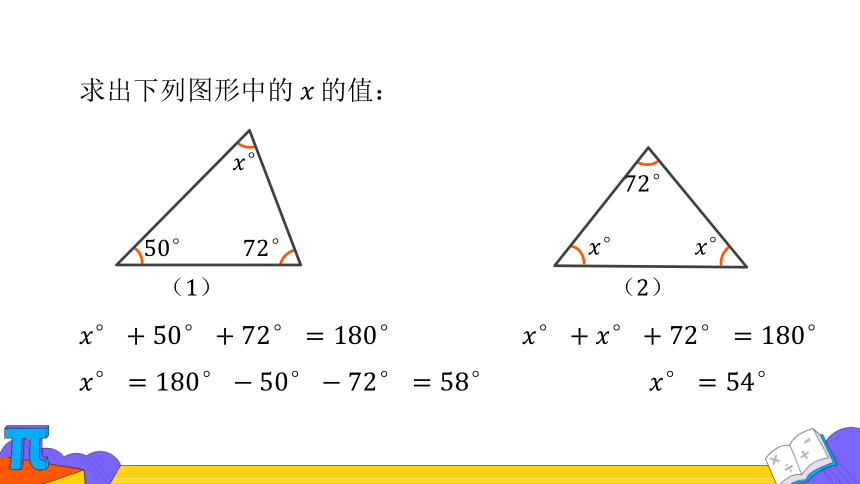
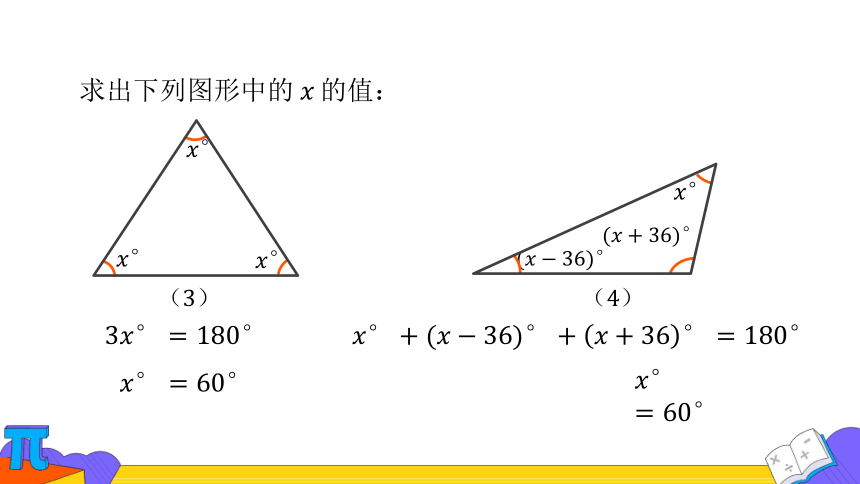
求出下列图形中的的值:
求出下列图形中的的值:
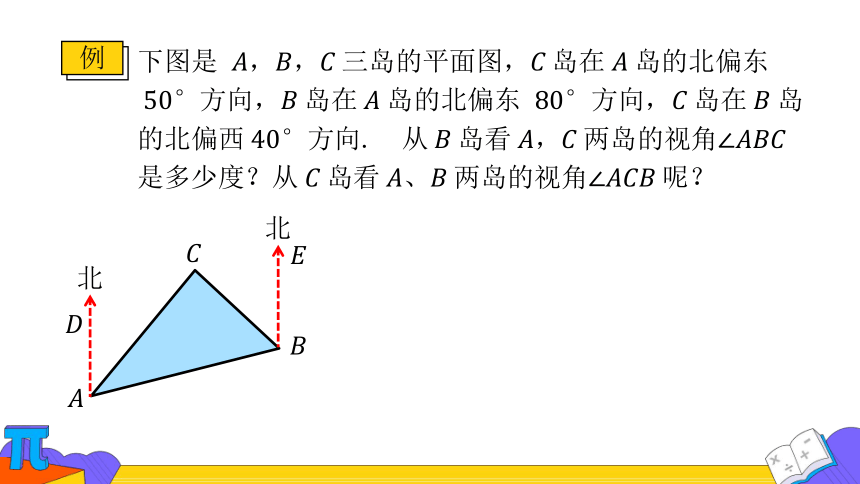
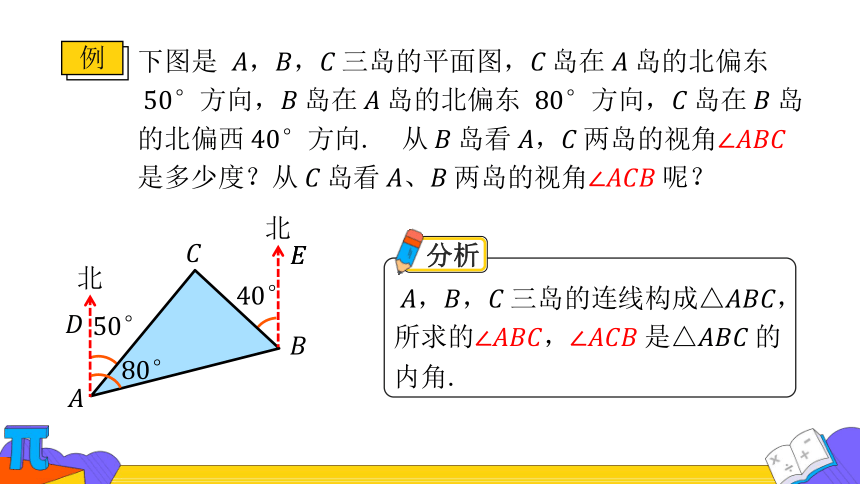
例
下图是 ,,三岛的平面图,岛在岛的北偏东方向,岛在岛的北偏东 方向,岛在岛的北偏西方向. 从岛看,两岛的视角是多少度?从岛看、两岛的视角呢?
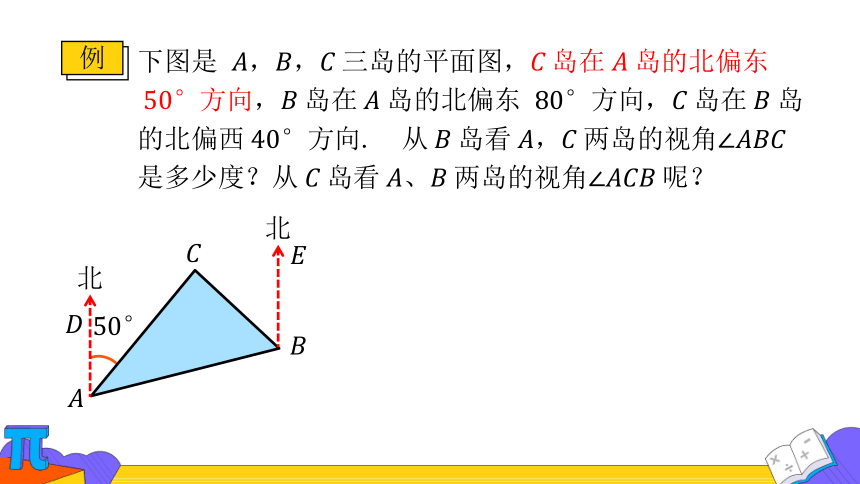
例
下图是 ,,三岛的平面图,岛在岛的北偏东方向,岛在岛的北偏东 方向,岛在岛的北偏西方向. 从岛看,两岛的视角是多少度?从岛看、两岛的视角呢?
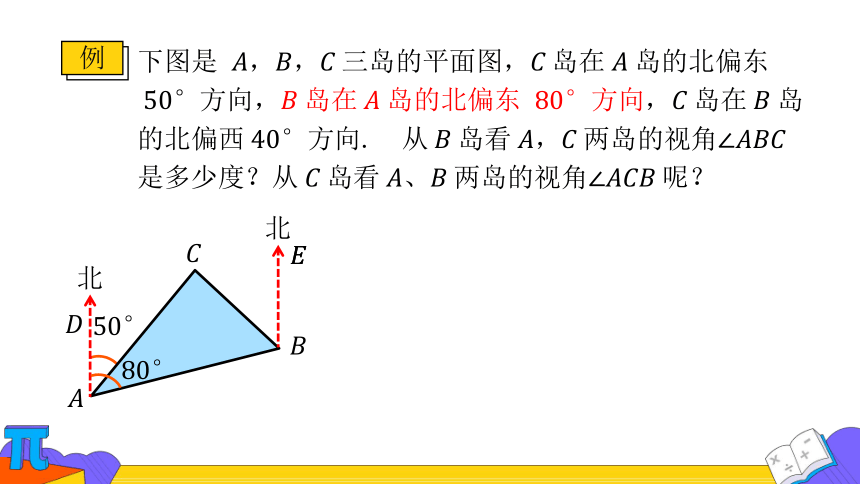
例
下图是 ,,三岛的平面图,岛在岛的北偏东方向,岛在岛的北偏东 方向,岛在岛的北偏西方向. 从岛看,两岛的视角是多少度?从岛看、两岛的视角呢?
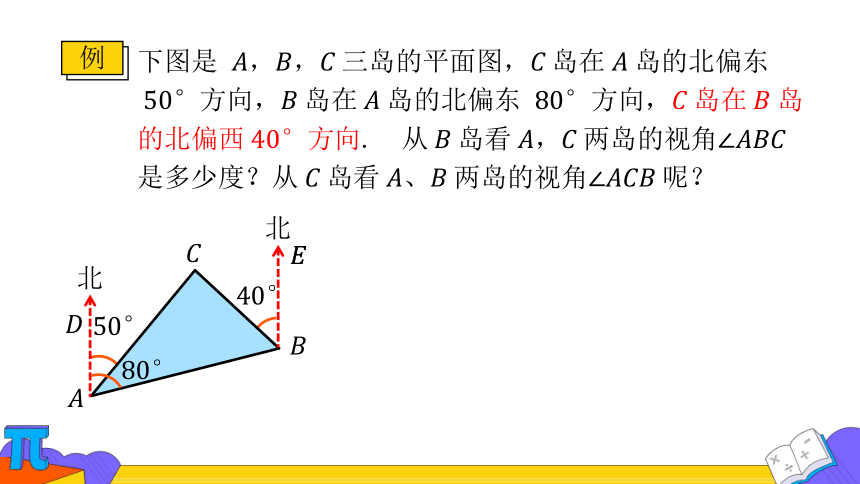
例
下图是 ,,三岛的平面图,岛在岛的北偏东方向,岛在岛的北偏东 方向,岛在岛的北偏西方向. 从岛看,两岛的视角是多少度?从岛看、两岛的视角呢?
分析
,,三岛的连线构成△,所求,是△的
内角.
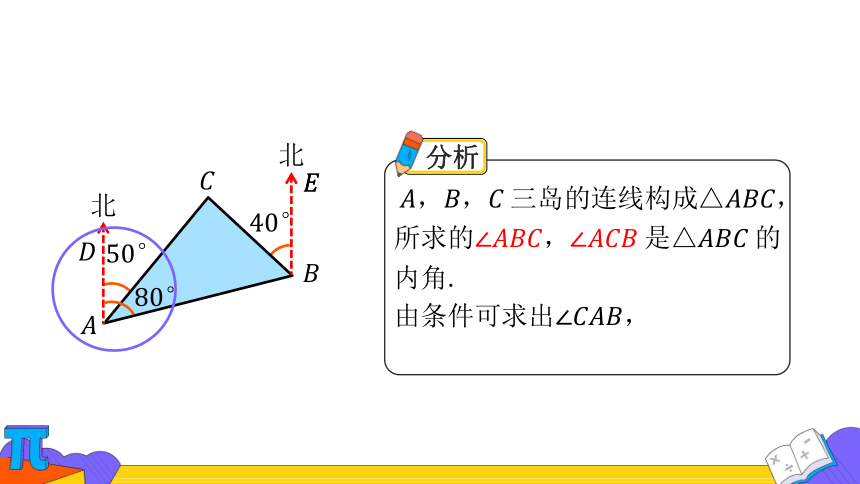
例
下图是 ,,三岛的平面图,岛在岛的北偏东方向,岛在岛的北偏东 方向,岛在岛的北偏西方向. 从岛看,两岛的视角是多少度?从岛看、两岛的视角呢?
分析
,,三岛的连线构成△,所求,是△的
内角.
由条件可求出,
分析
,,三岛的连线构成△,所求,是△的内角.
由条件可求出,如果还能求出,就能求.
.
由∥,得
.
所以
,
.
由∥,得
.
所以
,
△
.
答:从岛看,两岛的视角
是,从 岛看,两岛的视
角是.
你还能想出其它解法吗?
添加辅助线
分析
∥∥.
,
,
.
如图,从处观测处的仰角 ,再从 处观测 处的仰角. 从 处观测 ,两处的视角是多少?
练习
练习
如图,从处观测处的仰角 ,再从 处观测 处的仰角. 从 处观测 ,两处的视角是多少?
练习
如图,从处观测处的仰角 ,再从 处观测 处的仰角. 从 处观测 ,两处的视角是多少?
分析
是△的一个内角,在△中,,
如果能得到的度数,就能
.
练习
如图,从处观测处的仰角 ,再从 处观测 处的仰角. 从 处观测 ,两处的视角是多少?
分析
,是的邻补角,很容易得到
.
练习
如图,从处观测处的仰角 ,再从 处观测 处的仰角. 从 处观测 ,两处的视角是多少?
你能直接说出的度数吗
问题
在△中,若,你能求出 , 的度数吗?为什么?你能求出度数吗?你能得出什么结论?
在直角三角形△中,,
由三角形内角和定理,得
,
即,
所以.
直角三角形的两个锐角互余.
直角三角形可以用符号“△”表示,三角形 可以写成△.
直角三角形可以用符号“△”表示,三角形 可以写成△.
直角三角形的两个锐角互余.
在△中,
,
.
直角三角形可以用符号“△”表示,三角形 可以写成△.
例
如图,,,相交于点,与有什么关系?为什么?
例
分析
判断两个角的关系,首先需要知道这两个角分别在什么三角形中.
如图,,,相交于点,与有什么关系?为什么?
△
.
△
.
,
.
我们知道,如果一个三角形是直角三角形,那么这个三角形有两个内角互余. 反过来,你能得出什么结论呢?这个结论成立吗?如何验证你的想法?
问题
利用三角形内角和定理可得:
有两个角互余的三角形是直角三角形.
有两个角互余的三角形是直角三角形.
△
△.
如图,,,垂足为 ,与有什么关系?为什么?
练习
练习
如图,,,垂足为 ,与有什么关系?为什么?
练习
如图,,,垂足为 ,与有什么关系?为什么?
练习
如图,,,垂足为 ,与有什么关系?为什么?
练习
相等.
同角的余数相等.
如图,,,垂足为 ,与有什么关系?为什么?
若, , 则△的高吗?为什么?
变式
变式
若, , 则△的高吗?为什么?
变式
若, , 则△的高吗?为什么?
变式
若, , 则△的高吗?为什么?
变式
若, , 则△的高吗?为什么?
变式
有两个角互余的三角形是直角三角形.
是.
若, , 则△的高吗?为什么?
课堂小结
.本节课学习了哪些主要内容
三角形内角和定理的应用;
直角三角形的性质与判定.
课堂小结
.你是如何探索三角形的性质与判定的?它们是如何叙述的呢?
它们有什么区别与联系吗?
直角三角形的两个锐角互余;
有两个角互余的三角形是直角三角形.
课堂小结
.利用直角三角形的性质与判定分别可以解决哪些问题?
利用直角三角形的性质解决一些直角三角形中角的计算类的问题;
利用新的判定,得到一种新的判断一个三角形是否为直角三角形的方法.
课后作业
.如图,,,. 求的度数.
.如图,处在处南偏西的方向,处在处的南偏东
方向,处在处的北偏东 方向,求的度数.
南
北
( 第)
( )
教科书 习题
再 见
三角形的内角
(第二课时)
复习回顾
三角形的内角和定理的具体内容是什么?
三角形.
在中,.
我们在小学的实验基础上,发现了证明三角形内角和定理的方法,你还记得吗?
通过添加辅助线,利用平行线的性质和平角的定义进行证明.
求出下列图形中的的值:
求出下列图形中的的值:
例
下图是 ,,三岛的平面图,岛在岛的北偏东方向,岛在岛的北偏东 方向,岛在岛的北偏西方向. 从岛看,两岛的视角是多少度?从岛看、两岛的视角呢?
例
下图是 ,,三岛的平面图,岛在岛的北偏东方向,岛在岛的北偏东 方向,岛在岛的北偏西方向. 从岛看,两岛的视角是多少度?从岛看、两岛的视角呢?
例
下图是 ,,三岛的平面图,岛在岛的北偏东方向,岛在岛的北偏东 方向,岛在岛的北偏西方向. 从岛看,两岛的视角是多少度?从岛看、两岛的视角呢?
例
下图是 ,,三岛的平面图,岛在岛的北偏东方向,岛在岛的北偏东 方向,岛在岛的北偏西方向. 从岛看,两岛的视角是多少度?从岛看、两岛的视角呢?
分析
,,三岛的连线构成△,所求,是△的
内角.
例
下图是 ,,三岛的平面图,岛在岛的北偏东方向,岛在岛的北偏东 方向,岛在岛的北偏西方向. 从岛看,两岛的视角是多少度?从岛看、两岛的视角呢?
分析
,,三岛的连线构成△,所求,是△的
内角.
由条件可求出,
分析
,,三岛的连线构成△,所求,是△的内角.
由条件可求出,如果还能求出,就能求.
.
由∥,得
.
所以
,
.
由∥,得
.
所以
,
△
.
答:从岛看,两岛的视角
是,从 岛看,两岛的视
角是.
你还能想出其它解法吗?
添加辅助线
分析
∥∥.
,
,
.
如图,从处观测处的仰角 ,再从 处观测 处的仰角. 从 处观测 ,两处的视角是多少?
练习
练习
如图,从处观测处的仰角 ,再从 处观测 处的仰角. 从 处观测 ,两处的视角是多少?
练习
如图,从处观测处的仰角 ,再从 处观测 处的仰角. 从 处观测 ,两处的视角是多少?
分析
是△的一个内角,在△中,,
如果能得到的度数,就能
.
练习
如图,从处观测处的仰角 ,再从 处观测 处的仰角. 从 处观测 ,两处的视角是多少?
分析
,是的邻补角,很容易得到
.
练习
如图,从处观测处的仰角 ,再从 处观测 处的仰角. 从 处观测 ,两处的视角是多少?
你能直接说出的度数吗
问题
在△中,若,你能求出 , 的度数吗?为什么?你能求出度数吗?你能得出什么结论?
在直角三角形△中,,
由三角形内角和定理,得
,
即,
所以.
直角三角形的两个锐角互余.
直角三角形可以用符号“△”表示,三角形 可以写成△.
直角三角形可以用符号“△”表示,三角形 可以写成△.
直角三角形的两个锐角互余.
在△中,
,
.
直角三角形可以用符号“△”表示,三角形 可以写成△.
例
如图,,,相交于点,与有什么关系?为什么?
例
分析
判断两个角的关系,首先需要知道这两个角分别在什么三角形中.
如图,,,相交于点,与有什么关系?为什么?
△
.
△
.
,
.
我们知道,如果一个三角形是直角三角形,那么这个三角形有两个内角互余. 反过来,你能得出什么结论呢?这个结论成立吗?如何验证你的想法?
问题
利用三角形内角和定理可得:
有两个角互余的三角形是直角三角形.
有两个角互余的三角形是直角三角形.
△
△.
如图,,,垂足为 ,与有什么关系?为什么?
练习
练习
如图,,,垂足为 ,与有什么关系?为什么?
练习
如图,,,垂足为 ,与有什么关系?为什么?
练习
如图,,,垂足为 ,与有什么关系?为什么?
练习
相等.
同角的余数相等.
如图,,,垂足为 ,与有什么关系?为什么?
若, , 则△的高吗?为什么?
变式
变式
若, , 则△的高吗?为什么?
变式
若, , 则△的高吗?为什么?
变式
若, , 则△的高吗?为什么?
变式
若, , 则△的高吗?为什么?
变式
有两个角互余的三角形是直角三角形.
是.
若, , 则△的高吗?为什么?
课堂小结
.本节课学习了哪些主要内容
三角形内角和定理的应用;
直角三角形的性质与判定.
课堂小结
.你是如何探索三角形的性质与判定的?它们是如何叙述的呢?
它们有什么区别与联系吗?
直角三角形的两个锐角互余;
有两个角互余的三角形是直角三角形.
课堂小结
.利用直角三角形的性质与判定分别可以解决哪些问题?
利用直角三角形的性质解决一些直角三角形中角的计算类的问题;
利用新的判定,得到一种新的判断一个三角形是否为直角三角形的方法.
课后作业
.如图,,,. 求的度数.
.如图,处在处南偏西的方向,处在处的南偏东
方向,处在处的北偏东 方向,求的度数.
南
北
( 第)
( )
教科书 习题
再 见
