等腰三角形的复习[上学期]
文档属性
| 名称 | 等腰三角形的复习[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 920.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-12-04 20:54:00 | ||
图片预览





文档简介
课件21张PPT。等腰三角形的复习设计制作兼授课人
海 角 等边等角对性质定理判定定理推论1(三线合一定理)推论2等腰直角推论1(三角相等)推论2(一
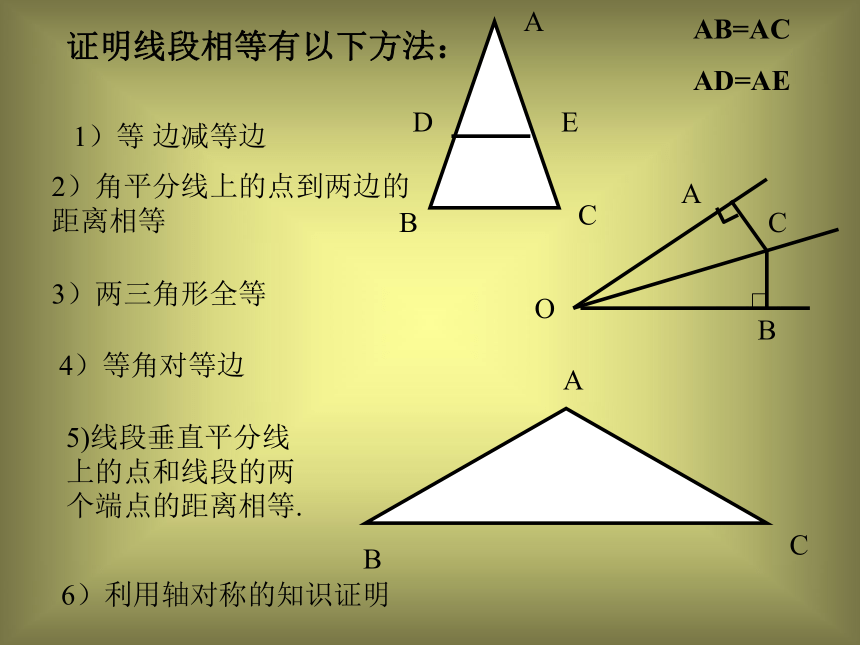
角是60°) 推论3(直角三角形)性质判定两腰相等证明线段相等有以下方法:1)等 边减等边2)角平分线上的点到两边的距离相等3)两三角形全等4)等角对等边AB=AC
AD=AE5)线段垂直平分线上的点和线段的两个端点的距离相等.6)利用轴对称的知识证明1、勾股定理及逆定理的内容及应用2、轴对称及轴对称图形的定义及性质
请回忆例1 已知:如图,等边△ABC的边长是 6 ㎝,
(1)查表求高AD的长(精确到0.1㎝);
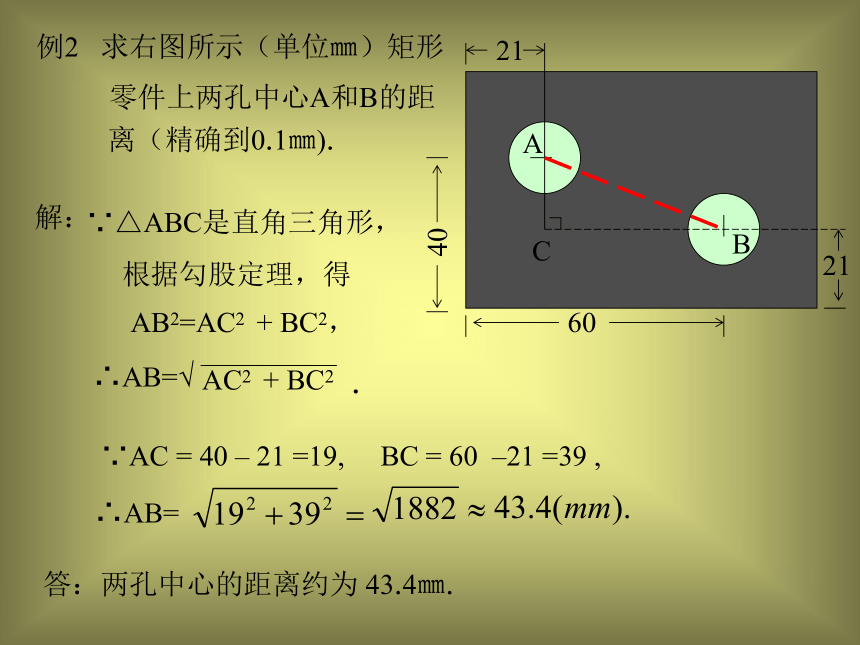
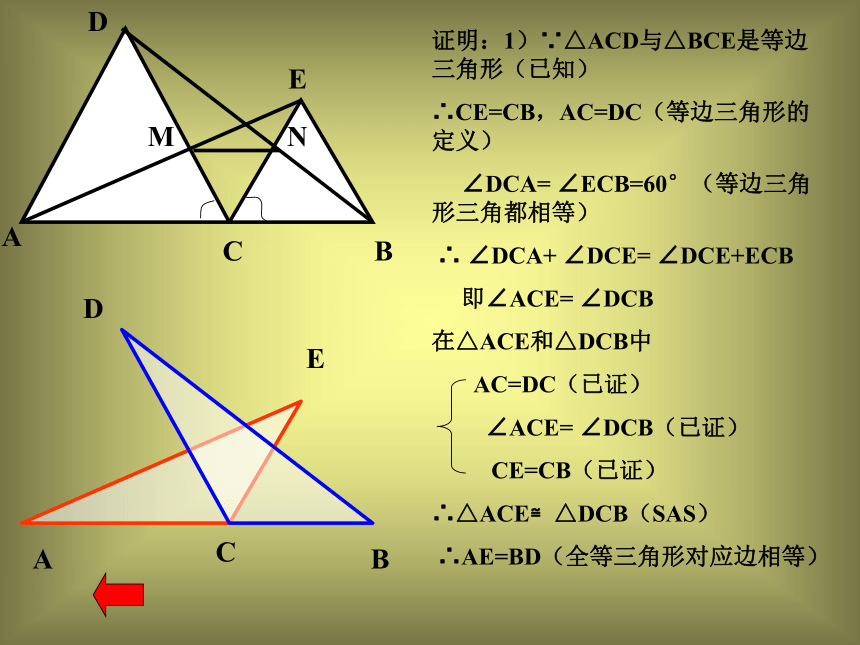
(2)求S△ABC(精确到0.1㎝2).ABCD∟解:(1)∵△ABC是等边三角形,AD是高,在Rt△ABD中,AB=6,BD=3,根据勾股定理,AD2=AB2 – BD2,∴AD=5.2(㎝);(2)例2 求右图所示(单位㎜)矩形零件上两孔中心A和B的距离(精确到0.1㎜).21402160ABC∟解:∵△ABC是直角三角形,根据勾股定理,得AB2=AC2 + BC2,∴AB=√AC2 + BC2 .∵AC = 40 – 21 =19, BC = 60 –21 =39 , ∴AB=答:两孔中心的距离约为 43.4㎜.例3:已知:如图,C是线段AB上一点,△ACD与△BCE是等边三角形,AE交CD于M,BD交EC于N,求证:1)AE=BD
2)CM=CN 3)MN∥AB ABCDEMN证明:1)证明:2)证明:3)BCEMNDA证明:1)∵△ACD与△BCE是等边三角形(已知)
∴CE=CB,AC=DC(等边三角形的定义)
∠DCA= ∠ECB=60°(等边三角形三角都相等)
∴ ∠DCA+ ∠DCE= ∠DCE+ECB
即∠ACE= ∠DCB
在△ACE和△DCB中
AC=DC(已证)
∠ACE= ∠DCB(已证)
CE=CB(已证)
∴△ACE≌△DCB(SAS)
∴AE=BD(全等三角形对应边相等)ACBDECEMNDABCEMNDABCEMNDAB证明:∵△ACE≌△DCB(已证)
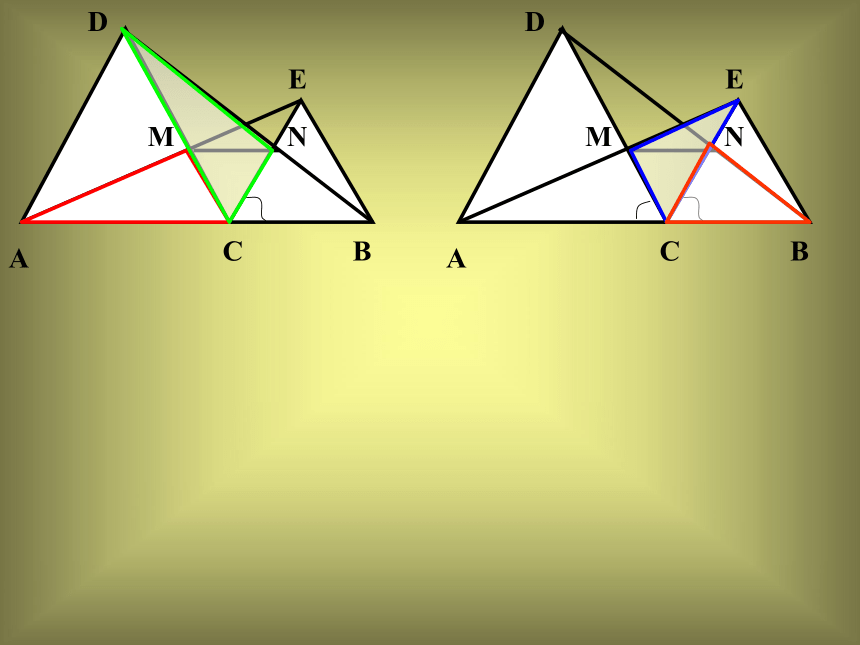
∴ ∠CAM= ∠CDN(全等三角形对应角相等)
∵ ∠DCA= ∠ECB=60°(已证)
∴ ∠MCN=180°-60°-60°= 60°(平角的定义)
∴ ∠DCA= ∠MCN=60°
在△ACM和△DCN中
∠CAM= ∠CDN(已证)
AC=DC(已证)
∠ACM= ∠MCN(已证)
∴△ACM≌△DCN(ASA)
∴ CM=CN(全等三角形对应角相等)DACMN已证: △ACE≌△DCB,已知两个等边三角形CEMNDA证明:∵CM=CN, ∠MCN=60°(已证)
∴△CMN是等边三角形(有一个角为60°
的等腰三角形是等边三角形)
∴ ∠MNC=60°(等边三角形的各角为60°)
∴ ∠ECB= ∠MNC=60°
∴MN∥AB(内错角相等两直线平行)
BACBMN60°60°已证:∠ACM= ∠BCN= ∠MCN=60°
CM=CN练习:已知:如图,△ABD和△ACE是等腰直角三角形∠DAB和∠EAC是直角,求证:①DC=BE
②DC⊥BEDBCAEODBCAEO△ABD和△ACE是等腰直角三角形证明:∵△ABD和△ACE是等腰直角三角形(已知)
∴AB=AD,AC=AE
∠BAD= ∠CAE=90°( 等腰直角三角形的定义)
∴ ∠BAD+ ∠BAC= ∠CAE+ ∠BAC即∠DAC= ∠BAE
在△ACD和△AEB中
AD=AB(已证)
∠DAC= ∠BAE(已证)
AC=AE(已证)
∴△ACD≌△AEB(SAS)
∴CD=BE(全等三角形对应边相等)DBCAEOOF△ACD≌△AEB证明:∵ △ACD≌△AEB(已证)
∴ ∠ACD= ∠AEB
∵ ∠AFE= ∠OFC(对顶角相等)
又∵ ∠AFE+ ∠AEF=90°
(直角三角形的两锐角互余)
∴ ∠OFC+ ∠ACD=90°(等量代换)
∵ ∠COF=180°-( ∠OFC+ ∠ACD)=180°-90°=90°(三角形的内角和定理)
∴CD⊥BE(垂直的定义)1、在△ABC中,AB=AC。
(1)若∠A=50°,则∠B= °,∠C= °;
(2)若∠B=45°,则∠A= °,∠C= °;
(3)若∠C=60°,则∠A= °,∠B= °;
(4)若∠A=B,则∠A= °,∠C= °。
?2、等腰三角形的一个角是30°,则它的底角是 。
?3、等腰三角形的周长是24cm,一边长是6cm,则其他两边的长分别是 。训练题一 填空题1、已知:如图,?ABC中,AB=AC,在AB上取一点D,又在AC的延长线上取一点E,使CE=BD,连结DE交BC于Q, DF∥AE。
求证:DQ=EQ分析:要证DQ=EQ,需证?DQF≌?EQC,
已知?DQF=?EQC,但条件不够。因为AB=AC∴?B=?ACB,又因为DF∥AE,所以?ACB=?DFB,所以?B=?DFB,所以DB=DF。DF=CE,?FDQ=?CEQ也可证,即?DQF≌?EQC可证。
证明:∵DF∥AE
∴?FDQ=?CEQ
?ACB=?DFB
∵AB=AC
∴?B=?ACB (等边对等角)
∴?B=?DFB
∴DB=DF (等角对等边)
∵CE=BD
∴CE=DF
∴?DFQ≌?ECQ (AAS)
∴DQ=EQ(全等三角形的性质) 2、已知等边?ABC的?B和?C的平分线相交于O,OB和OC的垂直平分线与BC相交于E、F。
求证:BE=EF=FC分析:因为GE、FH分别为OB、OC的垂直平分线,可知BE=OE,FC=OF,欲证BE=EF=FC,需证OE=OF=EF,只需证?OEF是等边三角形。
证明:连结OE、OF
∵?ABC是等边三角形 ∴?ABC=?ACB=60?
∵BO、CO分别平分?ABC和?ACB,
∴?OBE=?OCF=30?
∵EG,FH分别为OB、OC的垂直平分线
∴EB=EO,FC=FO ∴?EOB=?EBO=30?
?FCO=?FOC=30?
∴?OEF=?OFE=60?
∴?OEF是等边三角形。
∴OE=OF=EF
∴BE=EF=FC
3、已知:如图,?ABC中,AB=AC=10,BC=16,点D在BC上,DA⊥CA于A。
求:BD的长。分析:因为?ABC中,AB=AC,可作AE⊥BC于E,构造直角三角形,由已知条件,AE,CE,可求。根据勾股定理可列方程式求解 谢谢
海 角 等边等角对性质定理判定定理推论1(三线合一定理)推论2等腰直角推论1(三角相等)推论2(一
角是60°) 推论3(直角三角形)性质判定两腰相等证明线段相等有以下方法:1)等 边减等边2)角平分线上的点到两边的距离相等3)两三角形全等4)等角对等边AB=AC
AD=AE5)线段垂直平分线上的点和线段的两个端点的距离相等.6)利用轴对称的知识证明1、勾股定理及逆定理的内容及应用2、轴对称及轴对称图形的定义及性质
请回忆例1 已知:如图,等边△ABC的边长是 6 ㎝,
(1)查表求高AD的长(精确到0.1㎝);
(2)求S△ABC(精确到0.1㎝2).ABCD∟解:(1)∵△ABC是等边三角形,AD是高,在Rt△ABD中,AB=6,BD=3,根据勾股定理,AD2=AB2 – BD2,∴AD=5.2(㎝);(2)例2 求右图所示(单位㎜)矩形零件上两孔中心A和B的距离(精确到0.1㎜).21402160ABC∟解:∵△ABC是直角三角形,根据勾股定理,得AB2=AC2 + BC2,∴AB=√AC2 + BC2 .∵AC = 40 – 21 =19, BC = 60 –21 =39 , ∴AB=答:两孔中心的距离约为 43.4㎜.例3:已知:如图,C是线段AB上一点,△ACD与△BCE是等边三角形,AE交CD于M,BD交EC于N,求证:1)AE=BD
2)CM=CN 3)MN∥AB ABCDEMN证明:1)证明:2)证明:3)BCEMNDA证明:1)∵△ACD与△BCE是等边三角形(已知)
∴CE=CB,AC=DC(等边三角形的定义)
∠DCA= ∠ECB=60°(等边三角形三角都相等)
∴ ∠DCA+ ∠DCE= ∠DCE+ECB
即∠ACE= ∠DCB
在△ACE和△DCB中
AC=DC(已证)
∠ACE= ∠DCB(已证)
CE=CB(已证)
∴△ACE≌△DCB(SAS)
∴AE=BD(全等三角形对应边相等)ACBDECEMNDABCEMNDABCEMNDAB证明:∵△ACE≌△DCB(已证)
∴ ∠CAM= ∠CDN(全等三角形对应角相等)
∵ ∠DCA= ∠ECB=60°(已证)
∴ ∠MCN=180°-60°-60°= 60°(平角的定义)
∴ ∠DCA= ∠MCN=60°
在△ACM和△DCN中
∠CAM= ∠CDN(已证)
AC=DC(已证)
∠ACM= ∠MCN(已证)
∴△ACM≌△DCN(ASA)
∴ CM=CN(全等三角形对应角相等)DACMN已证: △ACE≌△DCB,已知两个等边三角形CEMNDA证明:∵CM=CN, ∠MCN=60°(已证)
∴△CMN是等边三角形(有一个角为60°
的等腰三角形是等边三角形)
∴ ∠MNC=60°(等边三角形的各角为60°)
∴ ∠ECB= ∠MNC=60°
∴MN∥AB(内错角相等两直线平行)
BACBMN60°60°已证:∠ACM= ∠BCN= ∠MCN=60°
CM=CN练习:已知:如图,△ABD和△ACE是等腰直角三角形∠DAB和∠EAC是直角,求证:①DC=BE
②DC⊥BEDBCAEODBCAEO△ABD和△ACE是等腰直角三角形证明:∵△ABD和△ACE是等腰直角三角形(已知)
∴AB=AD,AC=AE
∠BAD= ∠CAE=90°( 等腰直角三角形的定义)
∴ ∠BAD+ ∠BAC= ∠CAE+ ∠BAC即∠DAC= ∠BAE
在△ACD和△AEB中
AD=AB(已证)
∠DAC= ∠BAE(已证)
AC=AE(已证)
∴△ACD≌△AEB(SAS)
∴CD=BE(全等三角形对应边相等)DBCAEOOF△ACD≌△AEB证明:∵ △ACD≌△AEB(已证)
∴ ∠ACD= ∠AEB
∵ ∠AFE= ∠OFC(对顶角相等)
又∵ ∠AFE+ ∠AEF=90°
(直角三角形的两锐角互余)
∴ ∠OFC+ ∠ACD=90°(等量代换)
∵ ∠COF=180°-( ∠OFC+ ∠ACD)=180°-90°=90°(三角形的内角和定理)
∴CD⊥BE(垂直的定义)1、在△ABC中,AB=AC。
(1)若∠A=50°,则∠B= °,∠C= °;
(2)若∠B=45°,则∠A= °,∠C= °;
(3)若∠C=60°,则∠A= °,∠B= °;
(4)若∠A=B,则∠A= °,∠C= °。
?2、等腰三角形的一个角是30°,则它的底角是 。
?3、等腰三角形的周长是24cm,一边长是6cm,则其他两边的长分别是 。训练题一 填空题1、已知:如图,?ABC中,AB=AC,在AB上取一点D,又在AC的延长线上取一点E,使CE=BD,连结DE交BC于Q, DF∥AE。
求证:DQ=EQ分析:要证DQ=EQ,需证?DQF≌?EQC,
已知?DQF=?EQC,但条件不够。因为AB=AC∴?B=?ACB,又因为DF∥AE,所以?ACB=?DFB,所以?B=?DFB,所以DB=DF。DF=CE,?FDQ=?CEQ也可证,即?DQF≌?EQC可证。
证明:∵DF∥AE
∴?FDQ=?CEQ
?ACB=?DFB
∵AB=AC
∴?B=?ACB (等边对等角)
∴?B=?DFB
∴DB=DF (等角对等边)
∵CE=BD
∴CE=DF
∴?DFQ≌?ECQ (AAS)
∴DQ=EQ(全等三角形的性质) 2、已知等边?ABC的?B和?C的平分线相交于O,OB和OC的垂直平分线与BC相交于E、F。
求证:BE=EF=FC分析:因为GE、FH分别为OB、OC的垂直平分线,可知BE=OE,FC=OF,欲证BE=EF=FC,需证OE=OF=EF,只需证?OEF是等边三角形。
证明:连结OE、OF
∵?ABC是等边三角形 ∴?ABC=?ACB=60?
∵BO、CO分别平分?ABC和?ACB,
∴?OBE=?OCF=30?
∵EG,FH分别为OB、OC的垂直平分线
∴EB=EO,FC=FO ∴?EOB=?EBO=30?
?FCO=?FOC=30?
∴?OEF=?OFE=60?
∴?OEF是等边三角形。
∴OE=OF=EF
∴BE=EF=FC
3、已知:如图,?ABC中,AB=AC=10,BC=16,点D在BC上,DA⊥CA于A。
求:BD的长。分析:因为?ABC中,AB=AC,可作AE⊥BC于E,构造直角三角形,由已知条件,AE,CE,可求。根据勾股定理可列方程式求解 谢谢
