人教版>八年级上册13.1.2 线段的垂直平分线的性质 课件 (共15张PPT)
文档属性
| 名称 | 人教版>八年级上册13.1.2 线段的垂直平分线的性质 课件 (共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-20 10:26:02 | ||
图片预览

文档简介
(共15张PPT)
线段的垂直平分线的性质
(第二课时)
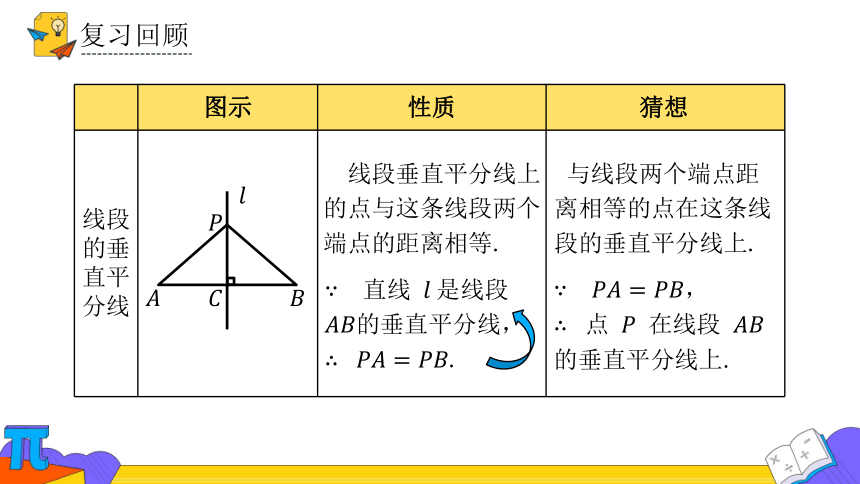
复习回顾
图示 性质
线段的垂直平分线
线段垂直平分线上的点与这条线段两个端点的距离相等.
直线 是线段 的垂直平分线,
.
猜想
,
点 在线段 的垂直平分线上.
与线段两个端点距离相等的点在这条线段的垂直平分线上.
只需证点 和 的中点 所连直线 是 的垂直平分线,
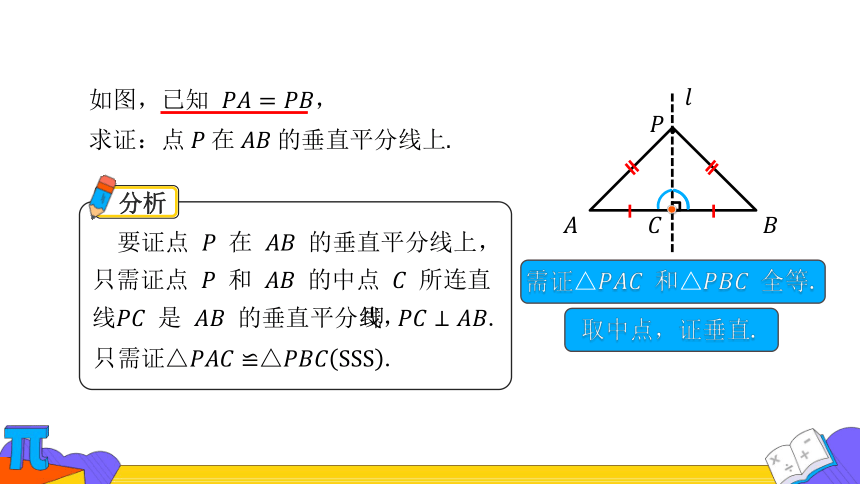
如图,已知 ,
要证点 在 的垂直平分线上,
分析
只需证△△.
取中点,证垂直.
即 .
需证△ 和△ 全等.
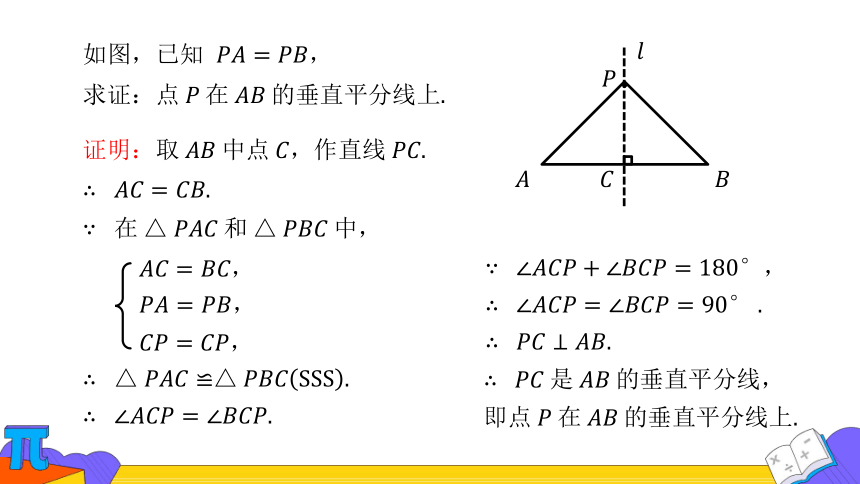
如图,已知 ,
,
,
如图,已知 ,
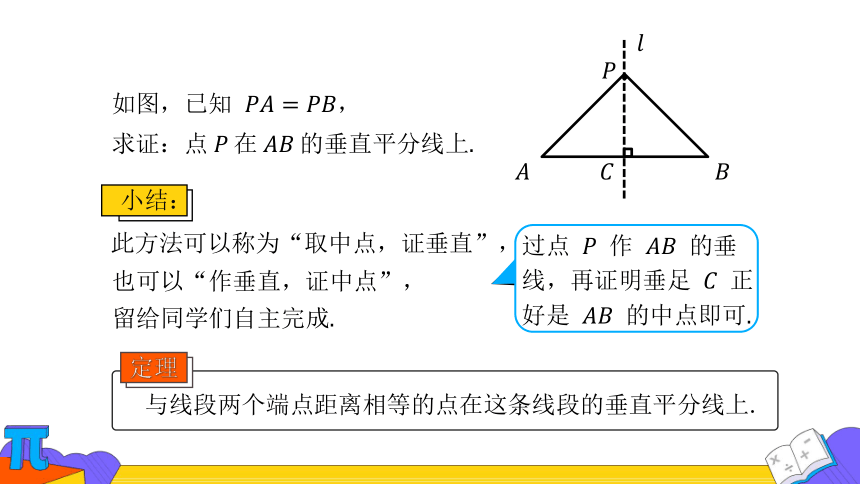
此方法可以称为“取中点,证垂直”,
也可以“作垂直,证中点”,
过点 作 的垂线,再证明垂足 正好是 的中点即可
留给同学们自主完成
与线段两个端点距离相等的点在这条线段的垂直平分线上.
定理
小结:
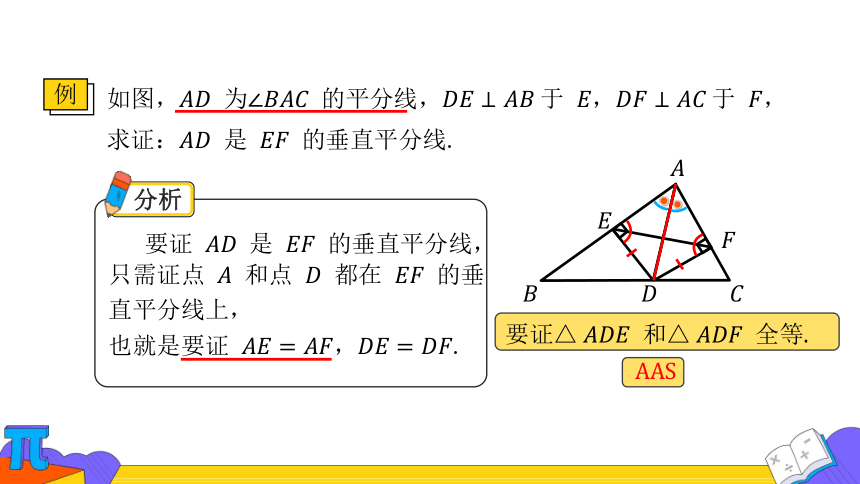
例
如图, 为 的平分线,于 ,于 ,
求证: 是 的垂直平分线.
要证 是 的垂直平分线,
也就是要证 .
分析
只需证点 和点 都在 的垂直平分线上,
要证 和 全等
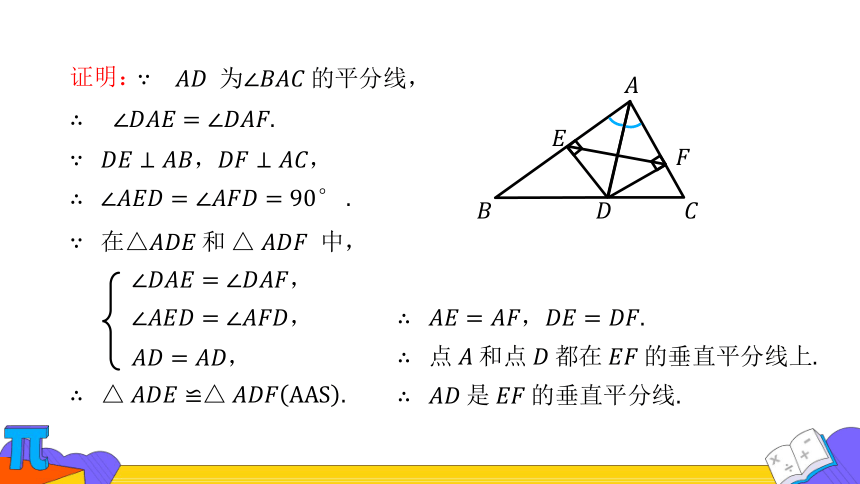
证明:
为的平分线,
△ 中,
,
,
例
如图,在△中,边 的垂直平分线 与边 的垂直平分线 交于点 ,分别交 于点 ,,已知△ 的周长为.
求的长;
求证:点 在 的垂直平分线上.
的垂直平分线是 ,
的垂直平分线是 ,
解:
.
,
例
如图,在△中,边 的垂直平分线 与边 的垂直平分线 交于点 ,分别交 于点 ,,已知△ 的周长为.
求的长;
求证:点 在 的垂直平分线上.
连接 ,,,
证明:
三角形三边的垂直平分线交于一点.
2
常见的辅助线:连接要证的垂直平分线上的点到线段两端点的距离;
1
小结
课
堂
小
结
与线段两个端点距离相等的点在这条线段的垂直平分线上.
定理:
课后作业
如图, 与 相交于点 ,,,.
求证: 垂直平分 .
1
课后作业
下面是小东设计的“作三角形一边上的高”的尺规作图过程.
2
.
,
.
.
课后作业
根据小东设计的尺规作图过程,
使用直尺和圆规,补全图形;(保留作图痕迹)
完成下面的证明.
.
再 见
线段的垂直平分线的性质
(第二课时)
复习回顾
图示 性质
线段的垂直平分线
线段垂直平分线上的点与这条线段两个端点的距离相等.
直线 是线段 的垂直平分线,
.
猜想
,
点 在线段 的垂直平分线上.
与线段两个端点距离相等的点在这条线段的垂直平分线上.
只需证点 和 的中点 所连直线 是 的垂直平分线,
如图,已知 ,
要证点 在 的垂直平分线上,
分析
只需证△△.
取中点,证垂直.
即 .
需证△ 和△ 全等.
如图,已知 ,
,
,
如图,已知 ,
此方法可以称为“取中点,证垂直”,
也可以“作垂直,证中点”,
过点 作 的垂线,再证明垂足 正好是 的中点即可
留给同学们自主完成
与线段两个端点距离相等的点在这条线段的垂直平分线上.
定理
小结:
例
如图, 为 的平分线,于 ,于 ,
求证: 是 的垂直平分线.
要证 是 的垂直平分线,
也就是要证 .
分析
只需证点 和点 都在 的垂直平分线上,
要证 和 全等
证明:
为的平分线,
△ 中,
,
,
例
如图,在△中,边 的垂直平分线 与边 的垂直平分线 交于点 ,分别交 于点 ,,已知△ 的周长为.
求的长;
求证:点 在 的垂直平分线上.
的垂直平分线是 ,
的垂直平分线是 ,
解:
.
,
例
如图,在△中,边 的垂直平分线 与边 的垂直平分线 交于点 ,分别交 于点 ,,已知△ 的周长为.
求的长;
求证:点 在 的垂直平分线上.
连接 ,,,
证明:
三角形三边的垂直平分线交于一点.
2
常见的辅助线:连接要证的垂直平分线上的点到线段两端点的距离;
1
小结
课
堂
小
结
与线段两个端点距离相等的点在这条线段的垂直平分线上.
定理:
课后作业
如图, 与 相交于点 ,,,.
求证: 垂直平分 .
1
课后作业
下面是小东设计的“作三角形一边上的高”的尺规作图过程.
2
.
,
.
.
课后作业
根据小东设计的尺规作图过程,
使用直尺和圆规,补全图形;(保留作图痕迹)
完成下面的证明.
.
再 见
