等腰三角形的复习[上学期]
文档属性
| 名称 | 等腰三角形的复习[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 16.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-12-06 15:07:00 | ||
图片预览





文档简介
课件13张PPT。 等腰三角形练习 等腰三角形的性质与判定
1.性质 性质定理:等腰三角形的两个底角相等。 定理:等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。
2.判定
定义: 有两边相等的三角形是等腰三角形。
判定定理:有两个角相等的三角形是等腰三角形复习等腰三角形性质与判定的应用 (1)计算角的度数 利用等腰三角形的性质,结合三角形内角和定理及推论计算角的度数,是等腰三角形性质的重要应用。 ①已知角的度数,求其它角的度数 ②已知条件中有较多的等腰三角形(此时往往设法用未知数表示图中的角,从中得到含这些未知数的方程或方程组) (2)证明线段或角相等 以等腰三角形为条件时的常用辅助线:
如图:若AB=AC
①作AD⊥BC于D,必有结论:∠1=∠2,BD=DC
②若BD=DC,连结AD,必有结论:∠1=∠2,AD⊥BC
③作AD平分∠BAC必有结论:AD⊥BC,BD=DC
作辅助线时,一定要作满足其中一个性质的辅助线,然后证出其它两个性质,不能这样作:作AD⊥BC,使∠1=∠2.1.等腰三角形顶角为36°,底角为_________。
2.等腰三角形顶角和一个底角之和为100°,则顶角度数为_____________。
3.等腰三角形两个角之比为4:1,则顶角为__________,底角为___________。
4.等腰三角形两边长为4、6,这个三角形周长为_____________。
5.已知△ABC中AB=AC,AB垂直平分线交AC于E,交AB于D,连结BE,若∠A=50°,∠EBC=__________。
6.△ABC中,AB=AC,AD⊥BC于D,若△ABC的周长为50,△ABD的周长为40,则AD=____________。
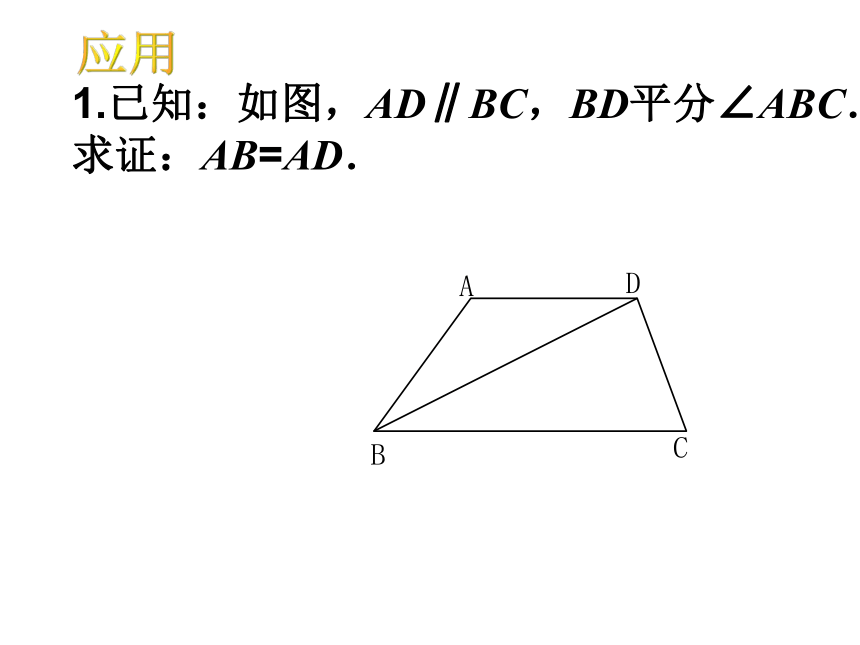
7.若等腰三角形顶角为n度,则腰上的高与底边的夹角为_____________。练习72°20° 1.已知:如图,AD∥BC,BD平分∠ABC.
求证:AB=AD.应用2: 已知:如图,房屋的顶角∠BAC=100 o, 过屋顶A的立柱AD ? BC , 屋椽AB=AC. 求顶架上∠B、∠C、∠BAD、
∠CAD的度数.
∴∠BAD=∠CAD=50°ABCD3.已知:△ABC中,AB=AC, AD=ED=EC. CD=BD, 求△ABC各角的度数。E4.已知:点D、E在△ABC中, AB=AC,AD=AE. 求证:BD=CE。ABCDE5.已知:如图,在△ABC中,AB=AC,O是△ABC内一点,且OB=OC。
求证:AO⊥BCC6.如图,已知在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD与CE相交于M点。求证:BM=CM。证明:∵AB=AC
∴∠ABC=∠ACB(等边对等角)
∴BD⊥AC于D,CE⊥AB于E
∴∠BEC=∠CDB=90°
∴∠1+∠ACB=90°,∠2+∠ABC=90°(直角三角形两个锐角互余)
∴∠1=∠2(等角的余角相等)
∴BM=CM(等角对等边)说明:本题易习惯性地用全等来证明,虽然也可以证明,但过程较复杂,应当多加强等腰三角形的性质和判定定理的应用。如图, △ABC中,AB=AC,D为AB上一点,E为AC延长线上一点,且BD=CE,DE交BC于G.求证:DG=EG.思路
因为△GDB和△GEC不全等,所以考虑在△GDB内作出一个与△GEC全等的三角形。★★思考题: 你有何收获?
1.性质 性质定理:等腰三角形的两个底角相等。 定理:等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。
2.判定
定义: 有两边相等的三角形是等腰三角形。
判定定理:有两个角相等的三角形是等腰三角形复习等腰三角形性质与判定的应用 (1)计算角的度数 利用等腰三角形的性质,结合三角形内角和定理及推论计算角的度数,是等腰三角形性质的重要应用。 ①已知角的度数,求其它角的度数 ②已知条件中有较多的等腰三角形(此时往往设法用未知数表示图中的角,从中得到含这些未知数的方程或方程组) (2)证明线段或角相等 以等腰三角形为条件时的常用辅助线:
如图:若AB=AC
①作AD⊥BC于D,必有结论:∠1=∠2,BD=DC
②若BD=DC,连结AD,必有结论:∠1=∠2,AD⊥BC
③作AD平分∠BAC必有结论:AD⊥BC,BD=DC
作辅助线时,一定要作满足其中一个性质的辅助线,然后证出其它两个性质,不能这样作:作AD⊥BC,使∠1=∠2.1.等腰三角形顶角为36°,底角为_________。
2.等腰三角形顶角和一个底角之和为100°,则顶角度数为_____________。
3.等腰三角形两个角之比为4:1,则顶角为__________,底角为___________。
4.等腰三角形两边长为4、6,这个三角形周长为_____________。
5.已知△ABC中AB=AC,AB垂直平分线交AC于E,交AB于D,连结BE,若∠A=50°,∠EBC=__________。
6.△ABC中,AB=AC,AD⊥BC于D,若△ABC的周长为50,△ABD的周长为40,则AD=____________。
7.若等腰三角形顶角为n度,则腰上的高与底边的夹角为_____________。练习72°20° 1.已知:如图,AD∥BC,BD平分∠ABC.
求证:AB=AD.应用2: 已知:如图,房屋的顶角∠BAC=100 o, 过屋顶A的立柱AD ? BC , 屋椽AB=AC. 求顶架上∠B、∠C、∠BAD、
∠CAD的度数.
∴∠BAD=∠CAD=50°ABCD3.已知:△ABC中,AB=AC, AD=ED=EC. CD=BD, 求△ABC各角的度数。E4.已知:点D、E在△ABC中, AB=AC,AD=AE. 求证:BD=CE。ABCDE5.已知:如图,在△ABC中,AB=AC,O是△ABC内一点,且OB=OC。
求证:AO⊥BCC6.如图,已知在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD与CE相交于M点。求证:BM=CM。证明:∵AB=AC
∴∠ABC=∠ACB(等边对等角)
∴BD⊥AC于D,CE⊥AB于E
∴∠BEC=∠CDB=90°
∴∠1+∠ACB=90°,∠2+∠ABC=90°(直角三角形两个锐角互余)
∴∠1=∠2(等角的余角相等)
∴BM=CM(等角对等边)说明:本题易习惯性地用全等来证明,虽然也可以证明,但过程较复杂,应当多加强等腰三角形的性质和判定定理的应用。如图, △ABC中,AB=AC,D为AB上一点,E为AC延长线上一点,且BD=CE,DE交BC于G.求证:DG=EG.思路
因为△GDB和△GEC不全等,所以考虑在△GDB内作出一个与△GEC全等的三角形。★★思考题: 你有何收获?
