人教版必修1第二章 匀变速直线运动的研究 单元测试(含答案)
文档属性
| 名称 | 人教版必修1第二章 匀变速直线运动的研究 单元测试(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-10-20 00:00:00 | ||
图片预览




文档简介
人教版必修1第二章 匀变速直线运动的研究 单元测试(素养提升)
一 、单选题(本大题共8小题,共48分)
1.(6分)一物体做匀变速直线运动,初速度,第内位移为零,则物体的加速度大小是
A. B. C. D.
2.(6分)物体自楼顶处自由落下,不计空气阻力,落到地面的速度为v,在此过程中,物体从楼顶落到楼高一半处所经历的时间为( )
A. B. C. D.
3.(6分)一滑雪运动员不借助雪杖,以的速度由坡底冲上一足够长的斜坡,当他返回坡底时测得速度大小为。已知上坡和下坡两个阶段运动员均沿同一直线做匀变速直线运动,则运动员上坡和下坡所用的时间之比为
A. : B. : C. : D. :
4.(6分)为了研究某品牌玩具车的性能,生产厂家拿两辆完全相同的玩具车做测试:将玩具甲、乙放在平直的轨道上同时沿同一起始线释放,已知两玩具车的运动方向相同,在该过程中通过计算机描绘了两玩具车速度的平方与位移的关系图像。则下列说法正确的是
A. 玩具车乙停止运动前两车的最大间距为
B. 玩具车甲、乙的加速度大小之比为:
C. 两玩具车在时再次并排
D. 时两玩具车的速度相等
5.(6分)身高1.70m的小宋同学在指示牌正下方原地竖直向上跳起,手指恰好能摸到指示牌的下边沿,经测量知指示牌下边沿到地面的竖直距离为2.50m。小宋同学双脚离地时速度大小最接近( )
A. 0.5m/s B. 3m/s C. 6m/s D. 9m/s
6.(6分)某质点从静止开始做匀加速直线运动,已知第秒内通过的位移是,则质点运动的加速度为
A. B. C. D.
7.(6分)、两木块自左向右做匀加速直线运动、现用高速摄机在同一底片上多次曝光,记录下木块每次曝光时的位置,如图所示,曝光的时间时间隔相等,则
A. 时刻,木块速度大于木块速度 B. 时刻,木块速度小于木块速度
C. 时刻,木块速度大于木块速度 D. 时刻,木块速度小于木块速度
8.(6分)一质点沿直线方向做减速直线运动,它离开点的距离随时间变化的关系为,它的速度随时间变化的关系为,则该质点在时的瞬时速度、从到间的平均速度、平均速率分别为
A. 、 、 B. 、 、
C. 、 、 D. 、 、
二 、多选题(本大题共4小题,共24分)
9.(6分)一辆汽车沿一直线运动,它的位移随时间变化的规律为:,则下列关于汽车的说法正确的是
A. 初速度为 B. 加速度为
C. 第秒末的速度为 D. 第一秒内的位移为
10.(6分)关于重力和自由落体加速度,下列说法正确的是
A. 物体所受重力的方向总是竖直向下
B. 物体所受重力的施力物体是地球
C. 地球表面的自由落体加速度随纬度的增大而减小
D. 质量大的物体受到的重力大,所以自由落体加速度也大
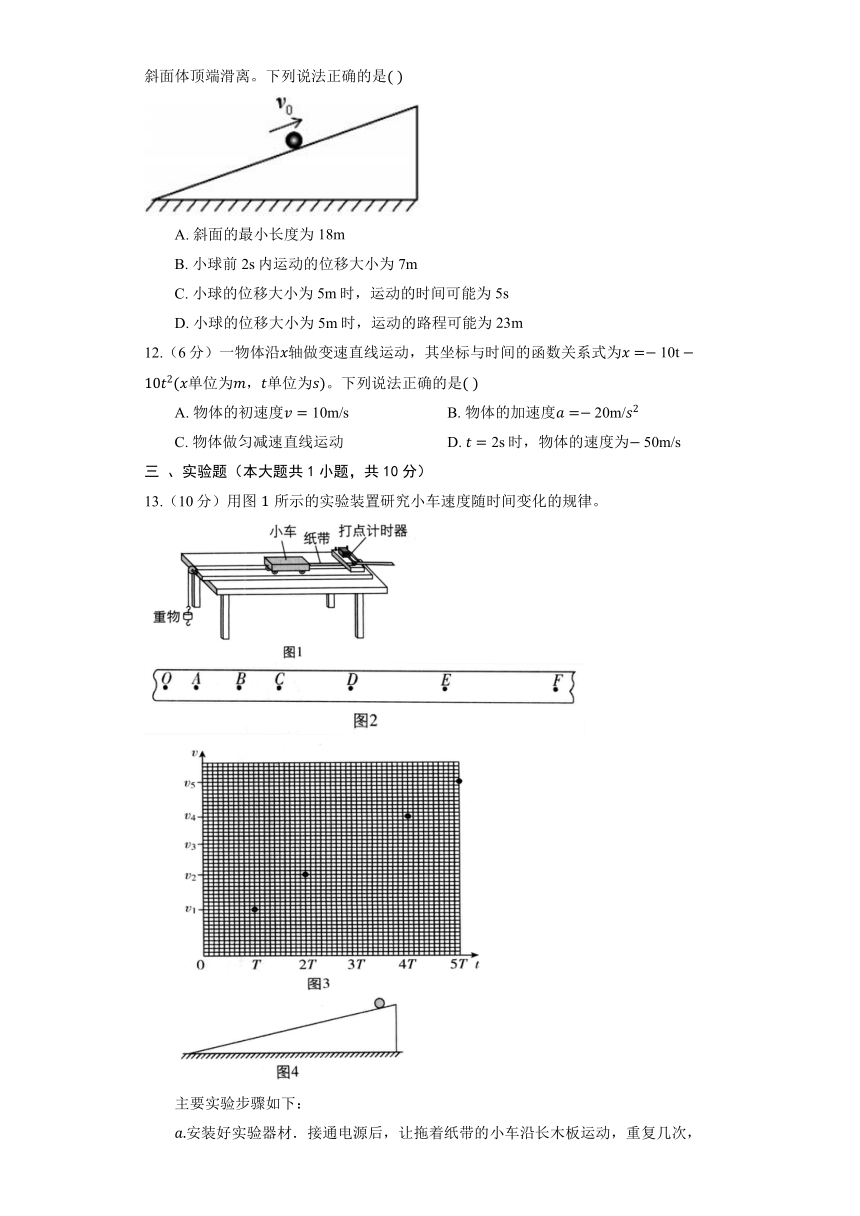
11.(6分)如图所示,光滑斜面体固定在水平地面上,其斜面中点的小球以沿斜面向上、大小为的初速度做匀变速直线运动,其加速度大小为,已知小球未从斜面体顶端滑离。下列说法正确的是
A. 斜面的最小长度为
B. 小球前内运动的位移大小为
C. 小球的位移大小为时,运动的时间可能为
D. 小球的位移大小为时,运动的路程可能为
12.(6分)一物体沿轴做变速直线运动,其坐标与时间的函数关系式为单位为,单位为。下列说法正确的是
A. 物体的初速度 B. 物体的加速度
C. 物体做匀减速直线运动 D. 时,物体的速度为
三 、实验题(本大题共1小题,共10分)
13.(10分)用图所示的实验装置研究小车速度随时间变化的规律。
主要实验步骤如下:
安装好实验器材.接通电源后,让拖着纸带的小车沿长木板运动,重复几次,
选出一条点迹清晰的纸带,找一个合适的点当作计时起点,然后每隔相同的时间间隔选取一个计数点,如图中、、、、、……所示,
通过测量、计算可以得到在打、、、、……点时小车的速度,分别记作、、、、……
以速度为纵轴、时间为横轴建立直角坐标系,在坐标纸上描点,如图所示,
结合上述实验步骤,请你完成下列任务:
在下列仪器和器材中,还需要使用的有________和________填选项前的字母,
A.电压合适的交流电源
B.电压可调的直流电源
C.刻度尺
D.秒表
E.天平含砝码
在图中已标出计数点、、、对应的坐标点,请在该图中标出计数点对应的坐标点,并画出图像;
观察图像,可以判断小车做匀变速直线运动,其依据是________,图像斜率的物理意义是_____________;
描绘图像前,还不知道小车是否做匀变速直线运动,用平均速度表示各计数点的瞬时速度,从理论上讲,对的要求是________填“越小越好”或“与大小无关”;从实验的角度看,选取的大小与速度测量的误差________填“有关”或“无关”;
早在世纪末,伽利略就猜想落体运动的速度应该是均匀变化的,当时只能靠滴水计时,为此他设计了如图所示的“斜面实验”,反复做了上百次,验证了他的猜想,请你结合匀变速直线运动的知识,分析说明如何利用伽利略“斜面实验”检验小球的速度是随时间均匀变化的。
四 、填空题(本大题共1小题,共6分)
14.(6分)某同学研究在固定斜面上运动物体的平均速度、瞬时速度和加速度之间的关系.使用的器材有:斜面、滑块、长度不同的矩形挡光片、光电计时器.
实验步骤如下:
①如图所示,将光电门固定在斜面下端附近;将一挡光片安装在滑块上,记下挡光片前端相对于斜面的位置,令滑块从斜面上方由静止开始下滑;
②当滑块上的挡光片经过光电门时,用光电计时器测得光线被挡光片遮住的时间;
③用表示挡光片沿运动方向的长度如图所示,表示滑块在挡光片遮住光线的时间内的平均速度大小,求出;
④将另一挡光片换到滑块上,使滑块上的挡光片前端与①中位置相同,令滑块由静止开始下滑,重复步骤②、③;
⑤多次重复步骤④;
⑥利用实验中得到的数据作出图,如图所示.
完成下列填空:
用表示滑块下滑的加速度大小,用表示挡光片前端到达光电门时滑块的瞬时速度大小,则与、和的关系式为__________.
由图可求得,_______,_______结果保留三位有效数字
五 、计算题(本大题共4小题,共48分)
15.(12分)一列货车从车站出发,沿平直铁路以加速度a=1m/做匀加速直线运动,则
(1)它在10s、20s、30s内的位移大小之比为多少?
(2)它在第1个10s、第2个10s、第3个10s内的位移大小之比为多少?
16.(12分)跳伞运动员作低空跳伞表演。他们离开飞机后先竖直向下做初速度为零的匀加速直线运动,加速度,离地面时打开降落伞。开伞后,由于受到很大的阻力,运动员马上又以的平地加速度作匀减速直线运动,到达地面时的速度为,求:
运动员刚离飞机时距地面的高度是多少米?
离开飞机后,经过多少秒的时间到达地面?保留小数点后两位
17.(12分)如图所示,一物体做匀变速直线运动,加速度为,从某时刻开始,将其运动时间等分成若干等份,每一份为。每一个时间内的位移分别为、、。试根据基本公式论证匀变速直线运动任意相邻相等时间间隔的位移差为一恒量,即。说明:推导过程中需要用到的但题目没有给出的物理量,要求做必要的说明。
18.(12分)如图,一段长为l=3m的棒,上端悬挂在天花板上P点,棒的正下方固定一个高为d=0.75m的中空圆筒Q.棒被释放后自由下落,不计空气阻力,它通过圆筒所经历的时间为t=0.5s.求圆筒上边缘离天花板的距离H.
答案和解析
1.【答案】B;
【解析】
物体做匀加速直线运动,由匀变速直线运动的位移公式和速度公式可以求得结果。
此题主要考查的就是匀变速直线运动的公式的应用,根据公式即可求得,比较简单。
设物体的加速度为,由速度公式可得物体在第末的速度为:,由物体的位移公式可得第内的位移为:,据题知,解得所以加速度的大小:,即加速度大小为,故正确,错误。
故选。
2.【答案】C;
【解析】略
3.【答案】B;
【解析】根据运动学公式,结合题意可以求出运动员上坡和下坡所用的时间之比。
在处理匀变速直线运动问题时,要注意熟记匀变速直线运动的基本公式和常用推论,要注意公式和推论的适用条件。
设运动员沿坡道运动的位移为,上坡时所用时间为,下坡时所用时间为,则根据运动学公式有
联立代入数据解得::
故错误,正确。
故选:。
4.【答案】D;
【解析】解:由图可知与成一次函数关系,故玩具车甲、乙均做匀变速直线运动,根据
分别代入数据可得,
则玩具车甲、乙的加速度大小之比为:,故错误;
由图可知,玩具车乙的初速度为
当两车速度相等时相距最远,设经过时间他,两车速度相等
即
解得
此时两玩具车的速度为
此时玩具车甲的位移为
玩具车乙的位移为
所以两玩具车在乙停止运动前的最大间距为
,故错误,正确;
C.根据速度时间关系可知,玩具车乙从开始到停止运动所用的时间
整个运动过程中玩具车乙的位移为
乙停止运动时玩具车甲的位移为
即玩具车乙停止一段时间后两玩具车再次并排,可得
代入数据解得,故错误。
故选:。
根据图像的斜率可以分别得到两车的加速度,当两车速度相等时两车间的距离最大;当两车再次并排的时候是乙停止运动后,甲再次追上乙的情况。
解本题的关键在于要知道该图像的斜率表示倍加速度,然后知道当二者速度相等时其间距离最大。根据位移关系可以得到相应的结果。
5.【答案】B;
【解析】略
6.【答案】B;
【解析】解:第秒内的位移,前秒内的位移
第秒内通过的位移
解得,故正确,错误;
故选:。
第秒内的位移等于秒内的位移减去秒内的位移,列出表达式,求出加速度。
解决本题关键掌握初速度为的匀变速直线运动的位移时间公式。
7.【答案】D;
【解析】解:、设曝光的时间时间隔为,设时刻木块速度大小分别为,物块做匀加速直线运动,在中间时刻的瞬时速度等于该段时间内的平均速度,有
由图可知,在时间内木块的位移等于木块的位移,两木块的平均速度相等,故时刻,木块速度等于木块速度,故错误;
、设曝光的时间时间隔为,设时刻物块的速度大小为,则根据运动学公式有
由图可知第一个时间内木块的位移小于木块的位移,又时刻,木块速度等于木块速度,故可知时刻,木块速度小于木块速度,故错误,正确。
故选:。
、物块做匀加速直线运动,在中间时刻的瞬时速度等于该段时间内的平均速度,结合图像比较时刻,木块速度等于木块速度;
、根据运动学公式,结合已知量判断时刻,木块速度小于木块速度。
在处理匀变速直线运动问题时,要注意公式的选择,比如求物体的位移时可以利用,也可以利用。
8.【答案】A;
【解析】解:该质点在时的瞬时速度为;
据题意,质点离开点的距离随时间变化的关系为,可得:
时,;
时,;
故内位移为:;
内的平均速度为:
当时,由得,,此时,在前内质点通过的路程为;
在后内通过的路程是;
则平均速率
故选:。
将代入,求解瞬时速度.根据题意得到时刻、时刻的位置坐标,求出内位移,然后根据平均速度的定义公式求解平均速度.根据的表达式求出速度减至零的时间,再由表达式求出质点通过的路程,即可求得平均速率.
本题关键根据题意求解出各个不同时刻物体的位置,然后求解各段时间的位移和平均速度;要明确位移等于位置坐标的变化,平均速度等于位移除以时间.平均速率等于路程除以时间,要注意研究质点的运动过程.
9.【答案】AC;
【解析】解:由运动学公式结合位移随时间的变化规律,由此可知,汽车的初速度,加速度;
、由分析可知,故正确,错误;
、当时,,故正确;
、当时,,故错误。
故选:。
根据位移时间公式和题中的公式对比,得到汽车的初速度和加速度,结合运动学公式做进一步判断。
此题主要考查了运动学公式的记忆和基本的应用,在计算的过程中要注意物理量的正负,难度不大。
10.【答案】AB;
【解析】重力的方向竖直向下,在地球上,随着纬度的升高重力加速度增大,自由落体运动的加速度与物体的质量无关.此题主要考查了重力、重力的加速度的基本概念,知道自由落体运动的加速度与物体质量无关,在地球上,不同的位置重力加速度不同.
解:、重力的方向竖直向下,故A正确.
B、物体所受重力的施力物体是地球,故B正确.
C、地球表面的自由落体加速度随纬度的增大而增大,故C错误.
D、自由落体运动的加速度与质量无关,轻重不同的物体在同一位置重力加速度相等,故D错误.
故选:.
11.【答案】ACD;
【解析】解:小球沿斜面向上做匀减速直线运动,最大位移为,因为小球从斜面中点沿斜面向上运动,所以斜面的最小长度为,故正确;
B.小球滑到斜面最高点所用时间,所以前小球速度未减小到,小球前内运动的位移为,故错误;
C.当小球位移为时,,代入数据解得:,,故运动的时间可能为,故正确;
D.依题意小球的位移可能为或者,
若小球的位移为,小球运动的路程可能为:
①
②
若小球的位移为,则小球运动的路程为
③
故正确。
故选:。
通过求出小球沿斜面向上的最大位移;先通过求出小球沿斜面向上运动到速度为零所用的时间,确定小球在内是否提前减速为零,再由求出前内的位移;通过求出小球位移为所用的时间;根据小球位移大小为,确定小球位移为或者,由小球运动的路径确定其路程的大小。
此题主要考查匀变速直线运动的理解,需要熟练匀变速直线运动的位移公式,注意本题中位移大小为,其位移可能为或者。
12.【答案】BD;
【解析】解:坐标与时间的函数关系式为,由可知,,
、物体的初速度为,故错误;
、物体的加速度,故正确;
、初速度,加速度,初速度和加速度方向相同,物体做匀加速运动,故错误;
、时,物体的速度为,故正确;
故选:。
根据匀变速直线运动的位移时间公式得出质点的初速度和加速度,结合速度时间公式求得速度。
解决本题的关键是知道速度与位移的关系、加速度与速度的关系,运用数学知识分析物体的运动情况。
13.【答案】,;
;
小车的速度随时间均匀变化,加速度;
越小越好,有关;
如果小球的速度随时间均匀变化,则小球的位移将随时间的平方均匀变化,因此可利用滴水法测出任意两个相邻且相等的时间内小球通过的位移差是否恒定来验证。;
【解析】
打点计时器使用的交流电源,选项正确,选项错误;
实验需要测出计数点间的距离,故还需要刻度尺,选项正确;
计数点间的时间间隔可通过纸带上打出的点测出,故不需要秒表,选项错误;
本实验不需要测小车的质量,选项错误;
先在图中描点,连线时让尽可能多的点在图线上,不在图线上的点尽量均匀分布在图线的两侧,如图所示:
;
图像的斜率表示小车的加速度,由于图线为倾斜直线,故小车做匀变速直线运动;
从理论上讲,越小,在该时间内的平均速度越接近瞬时速度,故越小越好;从实验的角度看,选取的大小与速度测量的误差有关;
如果小球的速度随时间均匀变化,则小球的位移将随时间的平方均匀变化,因此可利用滴水法测出任意两个相邻且相等的时间内小球通过的位移差是否恒定来验证。
14.【答案】 ;
【解析】
由于滑块做匀变速运动,在挡光片通过光电门的过程中,由运动学公式得,故
由结合图可知,图线与纵轴的交点的纵坐标即为,将图线延长与纵轴相交,得,图线的斜率等于,即,求得
15.【答案】(1)1∶4∶9 (2)1∶3∶5;
【解析】(1)根据位移—时间公式,可得它在10s、20s、30s内的位移大小分别为
==×1×m=50m
==×1×m=200m
==×1×m=450m
则位移之比为∶∶=1∶4∶9
(2)它在第1个10s、第2个10s、第3个10s内的位移大小分别为
==50m
=-=150m
=-=250m
位移之比为∶∶=50∶150∶250=1∶3∶5
16.【答案】解:(1)设打开降落伞时的速度为v,根据v′2-=2a′x
v==m/s=60m/s
则匀加速运动的位移为,==m=180m
得:h=+x=180+125m=305m.
(2)匀加速运动的时间为:
==s=10s
匀减速运动的时间为
==s=3.85s
则有:t=+=6+3.85s=9.85s.
答:(1)运动员离开飞机时距地面的高度为305m.
(2)离开飞机后,经过9.85s的时间才能到达地面.;
【解析】
根据匀变速直线运动的速度位移公式求出打开降落伞时的速度,结合速度位移公式求出匀加速运动的位移,结合匀减速运动的位移求出运动员离开飞机时的高度.
根据速度时间公式分别求出匀加速和匀减速运动的时间,从而得出离开飞机到达地面的总时间.
解决本题的关键理清运动员的运动过程,掌握匀变速直线运动的运动学公式,并能灵活运用.
17.【答案】证明:设物体在第一个T时间的初速度为
则在第一个T时间的位移为
在前2个T时间的位移为
在第二个T时间的位移
所以=aT2
得证Δs=aT2。;
【解析】
通过位移公式分别表示出任意相邻两段相等时间间隔的位移,然后通过位移相减即可得证。
此题主要考查匀变速直线运动的位移公式的运用,需要区分清楚第几个时间内和前几个时间内的概念,通过表达相邻相等时间间隔内的位移,然后作差即可得证。
18.【答案】见解析;
【解析】设棒释放后其下端到圆筒上边缘位置时间为,到圆筒下边缘位置时间为,
则t=- ①
=H-l ②
=H+d ③
联立①②③可解得H=4.25m
一 、单选题(本大题共8小题,共48分)
1.(6分)一物体做匀变速直线运动,初速度,第内位移为零,则物体的加速度大小是
A. B. C. D.
2.(6分)物体自楼顶处自由落下,不计空气阻力,落到地面的速度为v,在此过程中,物体从楼顶落到楼高一半处所经历的时间为( )
A. B. C. D.
3.(6分)一滑雪运动员不借助雪杖,以的速度由坡底冲上一足够长的斜坡,当他返回坡底时测得速度大小为。已知上坡和下坡两个阶段运动员均沿同一直线做匀变速直线运动,则运动员上坡和下坡所用的时间之比为
A. : B. : C. : D. :
4.(6分)为了研究某品牌玩具车的性能,生产厂家拿两辆完全相同的玩具车做测试:将玩具甲、乙放在平直的轨道上同时沿同一起始线释放,已知两玩具车的运动方向相同,在该过程中通过计算机描绘了两玩具车速度的平方与位移的关系图像。则下列说法正确的是
A. 玩具车乙停止运动前两车的最大间距为
B. 玩具车甲、乙的加速度大小之比为:
C. 两玩具车在时再次并排
D. 时两玩具车的速度相等
5.(6分)身高1.70m的小宋同学在指示牌正下方原地竖直向上跳起,手指恰好能摸到指示牌的下边沿,经测量知指示牌下边沿到地面的竖直距离为2.50m。小宋同学双脚离地时速度大小最接近( )
A. 0.5m/s B. 3m/s C. 6m/s D. 9m/s
6.(6分)某质点从静止开始做匀加速直线运动,已知第秒内通过的位移是,则质点运动的加速度为
A. B. C. D.
7.(6分)、两木块自左向右做匀加速直线运动、现用高速摄机在同一底片上多次曝光,记录下木块每次曝光时的位置,如图所示,曝光的时间时间隔相等,则
A. 时刻,木块速度大于木块速度 B. 时刻,木块速度小于木块速度
C. 时刻,木块速度大于木块速度 D. 时刻,木块速度小于木块速度
8.(6分)一质点沿直线方向做减速直线运动,它离开点的距离随时间变化的关系为,它的速度随时间变化的关系为,则该质点在时的瞬时速度、从到间的平均速度、平均速率分别为
A. 、 、 B. 、 、
C. 、 、 D. 、 、
二 、多选题(本大题共4小题,共24分)
9.(6分)一辆汽车沿一直线运动,它的位移随时间变化的规律为:,则下列关于汽车的说法正确的是
A. 初速度为 B. 加速度为
C. 第秒末的速度为 D. 第一秒内的位移为
10.(6分)关于重力和自由落体加速度,下列说法正确的是
A. 物体所受重力的方向总是竖直向下
B. 物体所受重力的施力物体是地球
C. 地球表面的自由落体加速度随纬度的增大而减小
D. 质量大的物体受到的重力大,所以自由落体加速度也大
11.(6分)如图所示,光滑斜面体固定在水平地面上,其斜面中点的小球以沿斜面向上、大小为的初速度做匀变速直线运动,其加速度大小为,已知小球未从斜面体顶端滑离。下列说法正确的是
A. 斜面的最小长度为
B. 小球前内运动的位移大小为
C. 小球的位移大小为时,运动的时间可能为
D. 小球的位移大小为时,运动的路程可能为
12.(6分)一物体沿轴做变速直线运动,其坐标与时间的函数关系式为单位为,单位为。下列说法正确的是
A. 物体的初速度 B. 物体的加速度
C. 物体做匀减速直线运动 D. 时,物体的速度为
三 、实验题(本大题共1小题,共10分)
13.(10分)用图所示的实验装置研究小车速度随时间变化的规律。
主要实验步骤如下:
安装好实验器材.接通电源后,让拖着纸带的小车沿长木板运动,重复几次,
选出一条点迹清晰的纸带,找一个合适的点当作计时起点,然后每隔相同的时间间隔选取一个计数点,如图中、、、、、……所示,
通过测量、计算可以得到在打、、、、……点时小车的速度,分别记作、、、、……
以速度为纵轴、时间为横轴建立直角坐标系,在坐标纸上描点,如图所示,
结合上述实验步骤,请你完成下列任务:
在下列仪器和器材中,还需要使用的有________和________填选项前的字母,
A.电压合适的交流电源
B.电压可调的直流电源
C.刻度尺
D.秒表
E.天平含砝码
在图中已标出计数点、、、对应的坐标点,请在该图中标出计数点对应的坐标点,并画出图像;
观察图像,可以判断小车做匀变速直线运动,其依据是________,图像斜率的物理意义是_____________;
描绘图像前,还不知道小车是否做匀变速直线运动,用平均速度表示各计数点的瞬时速度,从理论上讲,对的要求是________填“越小越好”或“与大小无关”;从实验的角度看,选取的大小与速度测量的误差________填“有关”或“无关”;
早在世纪末,伽利略就猜想落体运动的速度应该是均匀变化的,当时只能靠滴水计时,为此他设计了如图所示的“斜面实验”,反复做了上百次,验证了他的猜想,请你结合匀变速直线运动的知识,分析说明如何利用伽利略“斜面实验”检验小球的速度是随时间均匀变化的。
四 、填空题(本大题共1小题,共6分)
14.(6分)某同学研究在固定斜面上运动物体的平均速度、瞬时速度和加速度之间的关系.使用的器材有:斜面、滑块、长度不同的矩形挡光片、光电计时器.
实验步骤如下:
①如图所示,将光电门固定在斜面下端附近;将一挡光片安装在滑块上,记下挡光片前端相对于斜面的位置,令滑块从斜面上方由静止开始下滑;
②当滑块上的挡光片经过光电门时,用光电计时器测得光线被挡光片遮住的时间;
③用表示挡光片沿运动方向的长度如图所示,表示滑块在挡光片遮住光线的时间内的平均速度大小,求出;
④将另一挡光片换到滑块上,使滑块上的挡光片前端与①中位置相同,令滑块由静止开始下滑,重复步骤②、③;
⑤多次重复步骤④;
⑥利用实验中得到的数据作出图,如图所示.
完成下列填空:
用表示滑块下滑的加速度大小,用表示挡光片前端到达光电门时滑块的瞬时速度大小,则与、和的关系式为__________.
由图可求得,_______,_______结果保留三位有效数字
五 、计算题(本大题共4小题,共48分)
15.(12分)一列货车从车站出发,沿平直铁路以加速度a=1m/做匀加速直线运动,则
(1)它在10s、20s、30s内的位移大小之比为多少?
(2)它在第1个10s、第2个10s、第3个10s内的位移大小之比为多少?
16.(12分)跳伞运动员作低空跳伞表演。他们离开飞机后先竖直向下做初速度为零的匀加速直线运动,加速度,离地面时打开降落伞。开伞后,由于受到很大的阻力,运动员马上又以的平地加速度作匀减速直线运动,到达地面时的速度为,求:
运动员刚离飞机时距地面的高度是多少米?
离开飞机后,经过多少秒的时间到达地面?保留小数点后两位
17.(12分)如图所示,一物体做匀变速直线运动,加速度为,从某时刻开始,将其运动时间等分成若干等份,每一份为。每一个时间内的位移分别为、、。试根据基本公式论证匀变速直线运动任意相邻相等时间间隔的位移差为一恒量,即。说明:推导过程中需要用到的但题目没有给出的物理量,要求做必要的说明。
18.(12分)如图,一段长为l=3m的棒,上端悬挂在天花板上P点,棒的正下方固定一个高为d=0.75m的中空圆筒Q.棒被释放后自由下落,不计空气阻力,它通过圆筒所经历的时间为t=0.5s.求圆筒上边缘离天花板的距离H.
答案和解析
1.【答案】B;
【解析】
物体做匀加速直线运动,由匀变速直线运动的位移公式和速度公式可以求得结果。
此题主要考查的就是匀变速直线运动的公式的应用,根据公式即可求得,比较简单。
设物体的加速度为,由速度公式可得物体在第末的速度为:,由物体的位移公式可得第内的位移为:,据题知,解得所以加速度的大小:,即加速度大小为,故正确,错误。
故选。
2.【答案】C;
【解析】略
3.【答案】B;
【解析】根据运动学公式,结合题意可以求出运动员上坡和下坡所用的时间之比。
在处理匀变速直线运动问题时,要注意熟记匀变速直线运动的基本公式和常用推论,要注意公式和推论的适用条件。
设运动员沿坡道运动的位移为,上坡时所用时间为,下坡时所用时间为,则根据运动学公式有
联立代入数据解得::
故错误,正确。
故选:。
4.【答案】D;
【解析】解:由图可知与成一次函数关系,故玩具车甲、乙均做匀变速直线运动,根据
分别代入数据可得,
则玩具车甲、乙的加速度大小之比为:,故错误;
由图可知,玩具车乙的初速度为
当两车速度相等时相距最远,设经过时间他,两车速度相等
即
解得
此时两玩具车的速度为
此时玩具车甲的位移为
玩具车乙的位移为
所以两玩具车在乙停止运动前的最大间距为
,故错误,正确;
C.根据速度时间关系可知,玩具车乙从开始到停止运动所用的时间
整个运动过程中玩具车乙的位移为
乙停止运动时玩具车甲的位移为
即玩具车乙停止一段时间后两玩具车再次并排,可得
代入数据解得,故错误。
故选:。
根据图像的斜率可以分别得到两车的加速度,当两车速度相等时两车间的距离最大;当两车再次并排的时候是乙停止运动后,甲再次追上乙的情况。
解本题的关键在于要知道该图像的斜率表示倍加速度,然后知道当二者速度相等时其间距离最大。根据位移关系可以得到相应的结果。
5.【答案】B;
【解析】略
6.【答案】B;
【解析】解:第秒内的位移,前秒内的位移
第秒内通过的位移
解得,故正确,错误;
故选:。
第秒内的位移等于秒内的位移减去秒内的位移,列出表达式,求出加速度。
解决本题关键掌握初速度为的匀变速直线运动的位移时间公式。
7.【答案】D;
【解析】解:、设曝光的时间时间隔为,设时刻木块速度大小分别为,物块做匀加速直线运动,在中间时刻的瞬时速度等于该段时间内的平均速度,有
由图可知,在时间内木块的位移等于木块的位移,两木块的平均速度相等,故时刻,木块速度等于木块速度,故错误;
、设曝光的时间时间隔为,设时刻物块的速度大小为,则根据运动学公式有
由图可知第一个时间内木块的位移小于木块的位移,又时刻,木块速度等于木块速度,故可知时刻,木块速度小于木块速度,故错误,正确。
故选:。
、物块做匀加速直线运动,在中间时刻的瞬时速度等于该段时间内的平均速度,结合图像比较时刻,木块速度等于木块速度;
、根据运动学公式,结合已知量判断时刻,木块速度小于木块速度。
在处理匀变速直线运动问题时,要注意公式的选择,比如求物体的位移时可以利用,也可以利用。
8.【答案】A;
【解析】解:该质点在时的瞬时速度为;
据题意,质点离开点的距离随时间变化的关系为,可得:
时,;
时,;
故内位移为:;
内的平均速度为:
当时,由得,,此时,在前内质点通过的路程为;
在后内通过的路程是;
则平均速率
故选:。
将代入,求解瞬时速度.根据题意得到时刻、时刻的位置坐标,求出内位移,然后根据平均速度的定义公式求解平均速度.根据的表达式求出速度减至零的时间,再由表达式求出质点通过的路程,即可求得平均速率.
本题关键根据题意求解出各个不同时刻物体的位置,然后求解各段时间的位移和平均速度;要明确位移等于位置坐标的变化,平均速度等于位移除以时间.平均速率等于路程除以时间,要注意研究质点的运动过程.
9.【答案】AC;
【解析】解:由运动学公式结合位移随时间的变化规律,由此可知,汽车的初速度,加速度;
、由分析可知,故正确,错误;
、当时,,故正确;
、当时,,故错误。
故选:。
根据位移时间公式和题中的公式对比,得到汽车的初速度和加速度,结合运动学公式做进一步判断。
此题主要考查了运动学公式的记忆和基本的应用,在计算的过程中要注意物理量的正负,难度不大。
10.【答案】AB;
【解析】重力的方向竖直向下,在地球上,随着纬度的升高重力加速度增大,自由落体运动的加速度与物体的质量无关.此题主要考查了重力、重力的加速度的基本概念,知道自由落体运动的加速度与物体质量无关,在地球上,不同的位置重力加速度不同.
解:、重力的方向竖直向下,故A正确.
B、物体所受重力的施力物体是地球,故B正确.
C、地球表面的自由落体加速度随纬度的增大而增大,故C错误.
D、自由落体运动的加速度与质量无关,轻重不同的物体在同一位置重力加速度相等,故D错误.
故选:.
11.【答案】ACD;
【解析】解:小球沿斜面向上做匀减速直线运动,最大位移为,因为小球从斜面中点沿斜面向上运动,所以斜面的最小长度为,故正确;
B.小球滑到斜面最高点所用时间,所以前小球速度未减小到,小球前内运动的位移为,故错误;
C.当小球位移为时,,代入数据解得:,,故运动的时间可能为,故正确;
D.依题意小球的位移可能为或者,
若小球的位移为,小球运动的路程可能为:
①
②
若小球的位移为,则小球运动的路程为
③
故正确。
故选:。
通过求出小球沿斜面向上的最大位移;先通过求出小球沿斜面向上运动到速度为零所用的时间,确定小球在内是否提前减速为零,再由求出前内的位移;通过求出小球位移为所用的时间;根据小球位移大小为,确定小球位移为或者,由小球运动的路径确定其路程的大小。
此题主要考查匀变速直线运动的理解,需要熟练匀变速直线运动的位移公式,注意本题中位移大小为,其位移可能为或者。
12.【答案】BD;
【解析】解:坐标与时间的函数关系式为,由可知,,
、物体的初速度为,故错误;
、物体的加速度,故正确;
、初速度,加速度,初速度和加速度方向相同,物体做匀加速运动,故错误;
、时,物体的速度为,故正确;
故选:。
根据匀变速直线运动的位移时间公式得出质点的初速度和加速度,结合速度时间公式求得速度。
解决本题的关键是知道速度与位移的关系、加速度与速度的关系,运用数学知识分析物体的运动情况。
13.【答案】,;
;
小车的速度随时间均匀变化,加速度;
越小越好,有关;
如果小球的速度随时间均匀变化,则小球的位移将随时间的平方均匀变化,因此可利用滴水法测出任意两个相邻且相等的时间内小球通过的位移差是否恒定来验证。;
【解析】
打点计时器使用的交流电源,选项正确,选项错误;
实验需要测出计数点间的距离,故还需要刻度尺,选项正确;
计数点间的时间间隔可通过纸带上打出的点测出,故不需要秒表,选项错误;
本实验不需要测小车的质量,选项错误;
先在图中描点,连线时让尽可能多的点在图线上,不在图线上的点尽量均匀分布在图线的两侧,如图所示:
;
图像的斜率表示小车的加速度,由于图线为倾斜直线,故小车做匀变速直线运动;
从理论上讲,越小,在该时间内的平均速度越接近瞬时速度,故越小越好;从实验的角度看,选取的大小与速度测量的误差有关;
如果小球的速度随时间均匀变化,则小球的位移将随时间的平方均匀变化,因此可利用滴水法测出任意两个相邻且相等的时间内小球通过的位移差是否恒定来验证。
14.【答案】 ;
【解析】
由于滑块做匀变速运动,在挡光片通过光电门的过程中,由运动学公式得,故
由结合图可知,图线与纵轴的交点的纵坐标即为,将图线延长与纵轴相交,得,图线的斜率等于,即,求得
15.【答案】(1)1∶4∶9 (2)1∶3∶5;
【解析】(1)根据位移—时间公式,可得它在10s、20s、30s内的位移大小分别为
==×1×m=50m
==×1×m=200m
==×1×m=450m
则位移之比为∶∶=1∶4∶9
(2)它在第1个10s、第2个10s、第3个10s内的位移大小分别为
==50m
=-=150m
=-=250m
位移之比为∶∶=50∶150∶250=1∶3∶5
16.【答案】解:(1)设打开降落伞时的速度为v,根据v′2-=2a′x
v==m/s=60m/s
则匀加速运动的位移为,==m=180m
得:h=+x=180+125m=305m.
(2)匀加速运动的时间为:
==s=10s
匀减速运动的时间为
==s=3.85s
则有:t=+=6+3.85s=9.85s.
答:(1)运动员离开飞机时距地面的高度为305m.
(2)离开飞机后,经过9.85s的时间才能到达地面.;
【解析】
根据匀变速直线运动的速度位移公式求出打开降落伞时的速度,结合速度位移公式求出匀加速运动的位移,结合匀减速运动的位移求出运动员离开飞机时的高度.
根据速度时间公式分别求出匀加速和匀减速运动的时间,从而得出离开飞机到达地面的总时间.
解决本题的关键理清运动员的运动过程,掌握匀变速直线运动的运动学公式,并能灵活运用.
17.【答案】证明:设物体在第一个T时间的初速度为
则在第一个T时间的位移为
在前2个T时间的位移为
在第二个T时间的位移
所以=aT2
得证Δs=aT2。;
【解析】
通过位移公式分别表示出任意相邻两段相等时间间隔的位移,然后通过位移相减即可得证。
此题主要考查匀变速直线运动的位移公式的运用,需要区分清楚第几个时间内和前几个时间内的概念,通过表达相邻相等时间间隔内的位移,然后作差即可得证。
18.【答案】见解析;
【解析】设棒释放后其下端到圆筒上边缘位置时间为,到圆筒下边缘位置时间为,
则t=- ①
=H-l ②
=H+d ③
联立①②③可解得H=4.25m
