14-3 等腰三角形(1)[上学期]
文档属性
| 名称 | 14-3 等腰三角形(1)[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 222.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-12-06 00:00:00 | ||
图片预览



文档简介
课件12张PPT。等腰三角形ABC等腰三角形的定义: 有两条边相等的三角形叫做等腰三角形。相等的两条边AB和AC叫做 腰;
另一条边BC叫做 底边;
两腰所夹的角∠BAC叫做 顶角;
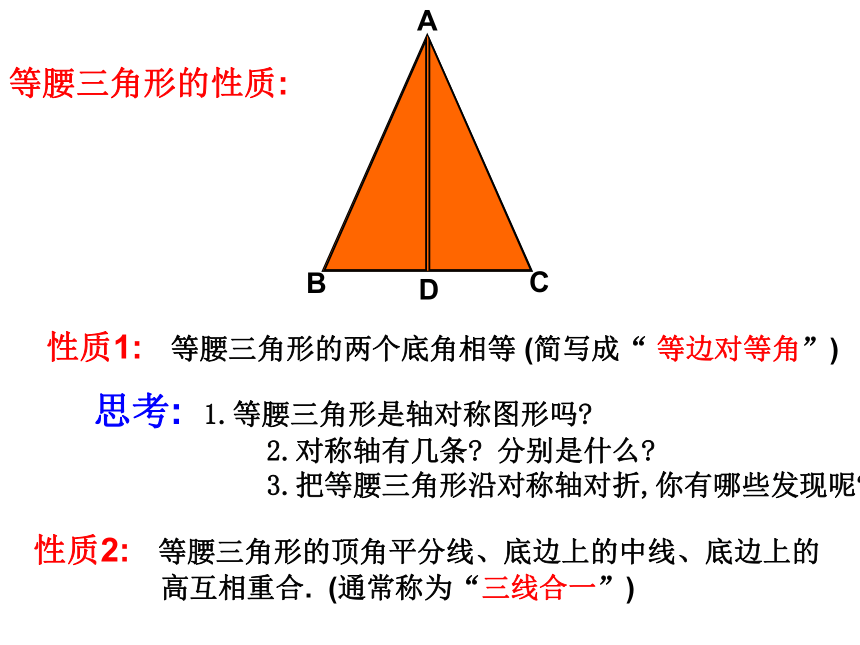
底边与腰的夹角∠ABC和∠ACB叫做 底角底角底角腰腰底边顶角ABCD等腰三角形的性质: 性质1: 等腰三角形的两个底角相等 (简写成“ 等边对等角”)性质2: 等腰三角形的顶角平分线、底边上的中线、底边上的
高互相重合. (通常称为“三线合一”)思考: 1.等腰三角形是轴对称图形吗?
2.对称轴有几条? 分别是什么?
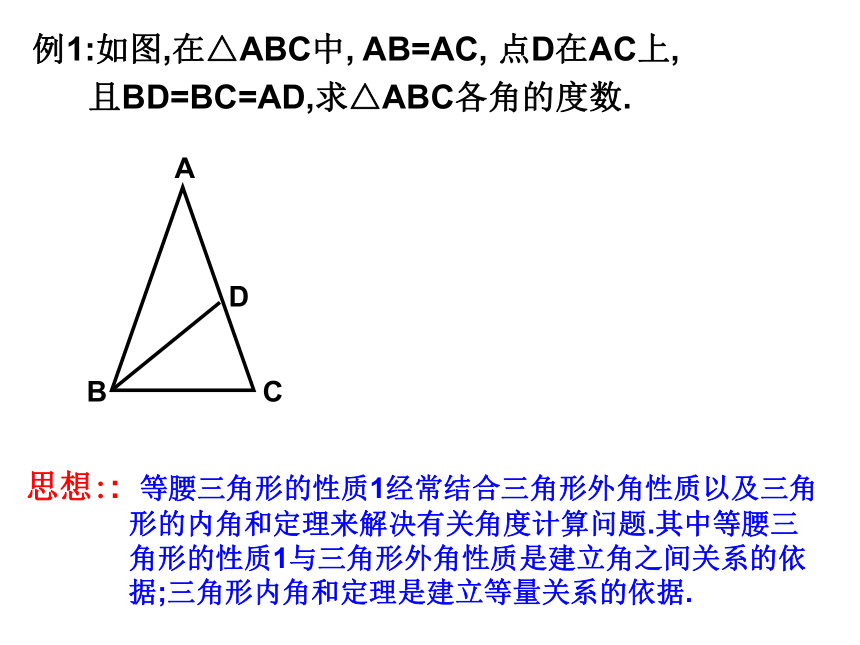
3.把等腰三角形沿对称轴对折,你有哪些发现呢?ABCD例1:如图,在△ABC中, AB=AC, 点D在AC上,
且BD=BC=AD,求△ABC各角的度数.思想:: 等腰三角形的性质1经常结合三角形外角性质以及三角
形的内角和定理来解决有关角度计算问题.其中等腰三
角形的性质1与三角形外角性质是建立角之间关系的依
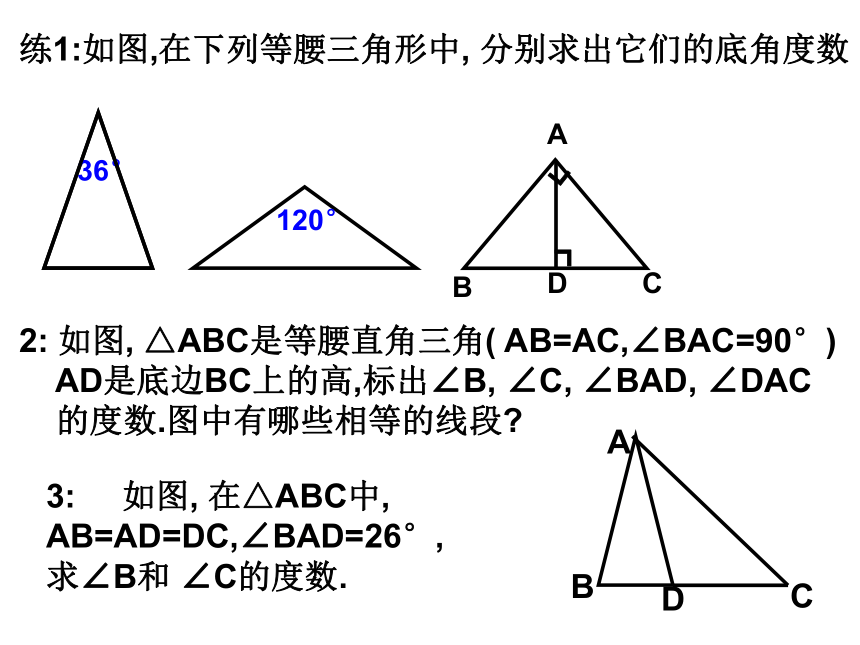
据;三角形内角和定理是建立等量关系的依据. 36°练1:如图,在下列等腰三角形中, 分别求出它们的底角度数2: 如图, △ABC是等腰直角三角( AB=AC,∠BAC=90°)
AD是底边BC上的高,标出∠B, ∠C, ∠BAD, ∠DAC
的度数.图中有哪些相等的线段?120°3: 如图, 在△ABC中, AB=AD=DC,∠BAD=26°,
求∠B和 ∠C的度数.4. 已知等腰三角形的一个角等于36°,那么它的另外两个
角的度数分别是 ;36°, 108°或72°, 72°6. 已知等腰三角形的一边长等于5,另一边长等于9, 那么
它的周长等于 ;19 或 237. 已知等腰三角形的一个外角等于100°, 那么它的顶角
的度数是 ;80°或50°5. 已知等腰三角形的一个角等于120°, 那么它的另外两
个角的度数是 ;30°, 30°8. 已知等腰三角形一角是另一角的2倍,则各内角的度数
分别是 ;45°, 45°, 90°,或72°, 72°, 36°ABCD(1)等腰三角形底边中点到两腰的距离相等吗?GH(2)DG,DH分别是AB、AC上的中线呢?讨论:9. 如图,已知点D,E在BC上, AB=AC,AD=AE.
求证:BD=CE交换结论与部分已知条件,命题还成立吗?10. 如图, AB=AE,∠ABC=∠AED,BC=ED,点F是CD的
中点.
(1)判断AF与CD的位置关系?为什么?ABCDEF(2)连接BE后,又能得出什么新的结论?不妨说出几个!练习判断下列语句是否正确。(1)等腰三角形的角平分线、中线和高互相重合。( )
(2)有一个角是60°的等腰三角形,其它两个
内角也为60°. ( )
(3)等腰三角形的底角都是锐角. ( )
(4)钝角三角形不可能是等腰三角形 . ( )××例 求证:如果三角形一个外角的平分线平行于
三角形的一边,那么这个三角形是等腰三角形。如图,∠CAE是⊿ABC的外角,∠1=∠2,
AD∥BC。
求证:AB=AC已知:经过本节课的学习,你有哪些收获?共同回顾
另一条边BC叫做 底边;
两腰所夹的角∠BAC叫做 顶角;
底边与腰的夹角∠ABC和∠ACB叫做 底角底角底角腰腰底边顶角ABCD等腰三角形的性质: 性质1: 等腰三角形的两个底角相等 (简写成“ 等边对等角”)性质2: 等腰三角形的顶角平分线、底边上的中线、底边上的
高互相重合. (通常称为“三线合一”)思考: 1.等腰三角形是轴对称图形吗?
2.对称轴有几条? 分别是什么?
3.把等腰三角形沿对称轴对折,你有哪些发现呢?ABCD例1:如图,在△ABC中, AB=AC, 点D在AC上,
且BD=BC=AD,求△ABC各角的度数.思想:: 等腰三角形的性质1经常结合三角形外角性质以及三角
形的内角和定理来解决有关角度计算问题.其中等腰三
角形的性质1与三角形外角性质是建立角之间关系的依
据;三角形内角和定理是建立等量关系的依据. 36°练1:如图,在下列等腰三角形中, 分别求出它们的底角度数2: 如图, △ABC是等腰直角三角( AB=AC,∠BAC=90°)
AD是底边BC上的高,标出∠B, ∠C, ∠BAD, ∠DAC
的度数.图中有哪些相等的线段?120°3: 如图, 在△ABC中, AB=AD=DC,∠BAD=26°,
求∠B和 ∠C的度数.4. 已知等腰三角形的一个角等于36°,那么它的另外两个
角的度数分别是 ;36°, 108°或72°, 72°6. 已知等腰三角形的一边长等于5,另一边长等于9, 那么
它的周长等于 ;19 或 237. 已知等腰三角形的一个外角等于100°, 那么它的顶角
的度数是 ;80°或50°5. 已知等腰三角形的一个角等于120°, 那么它的另外两
个角的度数是 ;30°, 30°8. 已知等腰三角形一角是另一角的2倍,则各内角的度数
分别是 ;45°, 45°, 90°,或72°, 72°, 36°ABCD(1)等腰三角形底边中点到两腰的距离相等吗?GH(2)DG,DH分别是AB、AC上的中线呢?讨论:9. 如图,已知点D,E在BC上, AB=AC,AD=AE.
求证:BD=CE交换结论与部分已知条件,命题还成立吗?10. 如图, AB=AE,∠ABC=∠AED,BC=ED,点F是CD的
中点.
(1)判断AF与CD的位置关系?为什么?ABCDEF(2)连接BE后,又能得出什么新的结论?不妨说出几个!练习判断下列语句是否正确。(1)等腰三角形的角平分线、中线和高互相重合。( )
(2)有一个角是60°的等腰三角形,其它两个
内角也为60°. ( )
(3)等腰三角形的底角都是锐角. ( )
(4)钝角三角形不可能是等腰三角形 . ( )××例 求证:如果三角形一个外角的平分线平行于
三角形的一边,那么这个三角形是等腰三角形。如图,∠CAE是⊿ABC的外角,∠1=∠2,
AD∥BC。
求证:AB=AC已知:经过本节课的学习,你有哪些收获?共同回顾
